模糊综合评价法原理及案例分析讲解

模糊数学绪论

用数学的眼光看世界，可把我们身边的现象划分为:

1. 确定性现象：如水加温到100C就沸腾，这种现象的规律性靠经典数学去刻画;
2. 随机现象：如掷筛子，观看那一面向上，这种现象的规律性靠概率统计去刻画;
3. 模糊现象：如“今天天气很热”，“小伙子很帅”，…。

此话准确吗？有多大的水分？靠模糊数学去刻画。

---

---

一、概述

1. 数学中研究的量的划分

量分为 确定性 和 不确定性：

确定性：

1. 经典数学（几何、代数）

不确定性：

1. 随机性（概率论、随机过程）
2. 灰性（灰色系统）
3. 模糊性（模糊数学）

---

2. 模糊综合评价模型

  模糊综合评价法是一种基于 模糊数学 的综合 评价方法。该综合评价法根据模糊数学的 隶属度理论 把定性评价转化为定量评价，即用模糊数学对受到多种因素制约的事物或对象做出一个总体的评价。
  它具有结果清晰，系统性强的特点，能较好地解决模糊的、难以量化的问题，适合各种 非确定性问题的解决。

---

二、经典集合和模糊集合的基本概念

1. 经典集合（classical set）和特征函数

• 经典集合：具有相同属性的事物的集体，例如：颜⾊、性别、⼿机、品牌等、⾃然数集。

• 集合的基本属性：（1）若 $a\in A$，$b\in A$，则 $a\ne b$，这是 互斥性 的体现。（2）$a\in A$ 和 $a\notin A$，有且仅有之一发生，这是 确定性 的体现。

• 数学中对于经典集合的刻画：特征函数
  
  ${\mathbf{f}}_{\mathbf{A}}:\mathbf{U}\to \{0,1\}$

  其中：$\to$ 代表定义，$U$ 代表论域（我们感兴趣的一些对象的集合），$f_a$ 表示 $A$ 集合的特征函数。例：
  $$\begin{gathered} 成绩及格的集合A=\{60,61,\cdots ,100\} \\ {f}_A=\{\begin{array}{l}\text{1,成绩≥60}\\ \text{0,成绩＜60}\end{array}，U是全班成绩的一个集合\{65,77,\cdots ,36\} \\ {f}_A=\{\begin{array}{l}\text{1},x\in A\\ 0,x\notin A\end{array}，\forall x\in U(注：U可看作是定义域，\{0,1\}可看作是值域) \end{gathered}$$

---

2. 模糊集合（fuzzy set）和隶属函数

• 模糊集合：用来描述模糊性概念的集合。（帅、高、白、年轻…）
• 与经典集合相比，模糊集合承认 亦此亦彼
• 数学中对于模糊集合的刻画： 隶属函数
  
  ${\mathbf{u}}_{\mathbf{A}}:\mathbf{U}\to [0,1]$
  其中注意与{o,1} 的区别，{0，1}只有两种可能，[0,1]有无数种可能。
  例：$A$ =”年轻“（年轻时一个模糊的概念），$U$ =（0，150）表示年龄的集合。隶属函数如下：
  $$u_A=\{\begin{array}{l}\text{1 ,0＜x＜20}\\ \text{(}40-x)/20,0\le x\le 20\\ \text{0 , 40＜x＜150}\end{array}$$

注意：隶属函数不唯一!
对于 U 中每一个元素，均对应于A中的一个隶属度，隶属度介于[0,1]，隶属度越大越属于这种集合。
注：若对于一个模糊集合 $A$ 我们给定一个隶属函数 $u_A$，那么我们可以将 $A$ 和 $u_A$ 视为等同。（方便表示，即$A(x)=u_A(x)$ ）

---

三、隶属函数的三种确定方法

1. 模糊统计法

原理：找多个人与对一个模糊概念进行描述（例如发放问卷调查），用隶属频率去定义隶属度。
这种方法只需要了解。

---

2. 借助已有的客观尺度

需要有合适的指标 , 并能收集到数据。

注：找到的指标必须介于0和1之间，否则需要做归一化处理。
恩格尔系数(%) = 视频指出总额/家庭或个人消费支出总额×100%。随着家庭和个⼈收⼊增加，收⼊中⽤于⻝品⽅⾯的⽀出⽐例将逐渐减⼩，这⼀定律被称为恩格尔定律。

---

3. 指派法

根据问题的性值直接套用某些分布作为隶属函数，主观性较强。

其中，梯形分布用得较多。下面用例题进行说明：

例：已知某一天的 SO2 的浓度为0.07mg/m^3，大气污染物中关于 SO2 的评价标准如下表，要求计算 SO2 在每一个等级中的隶属度。

解：I级为偏小型，Ⅱ级和Ⅲ级为中间型，Ⅳ级为偏大型。（这里的确定主要是根据 偏向指定值 来划分）

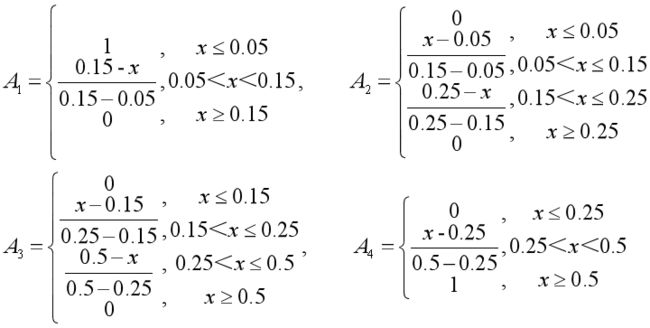
(等号在哪边无所谓，一般使用梯形分布最为简单)
则：A1(0.07)=0.8，A2(0.07)=0.2，A3(0.07)=0，A4(0.07)=0

---

四 、 应用：模糊综合评价( 评判 )

1. 评价问题概述

模糊评价问题是要解决的问题是：
  1. 把论域中的对象对应评语集中的一个指定的评语
  2. 将方案作为评语集并选择一个最优的方案。

在模糊综合评价中，引入三个集合：（下面的符号和概念中的符号表示的 含义不同）

1. 因素集（评价指标集）  U = {u1,u2,…,un}
2. 评语集（评价的结果集） V = {v1,v2,…,vm}
3. 权重集（指标的权重）  A = {a1,a2,…,an}

例：评价一名学生的表现，U = {专业排名，课外实践，志愿服务，竞赛成绩}，V = {优，良，差}，A = {0.5，0.1，0.1，0.3}

---

2. 一级模糊综合评价

一级模糊综合评价分为以下五个步骤：

1. 确定因素集
2. 确定评语集
3. 确定该因素的权重
4. 确定模糊综合判断矩阵
5. 综合评判

那么我们分析一下下面的两道例题

---

例1：某单位对员工的年终综合判定

第一步：确定因素集

  对员工的表现，需要从多个方面进行综合评判，如员工的工作业绩、工作态度、沟通能力、政治表现等。所有这些因素构成了评价指标体系集合，即因素集，记为 $U=u_1,u_2,\cdots ,u_n$。

  注意：一级模糊评价中，n 往往较小（一般 ≤ 5）且 指标间相关性不强。

  取因素集：U = {工作业绩u1，工作态度u1，沟通能力u3，政治表现u4 }

---

第二步：确定评语集

  由于每个指标的评价值的不同，往往会形成不同的等级。如对工作业绩的评价有好、较好、中等、较差、很差等。由各种不同决断构成的集合称为评语集，记为$V=v_1,v_2,\cdots ,v_m$。

  注意：这里评语集中有 m 个元素， m 与 n 无关。

  取评语集：V={优秀v1，良好v，一般v3，较差v4，很差v5 }

---

第三步：确定各因素的权重

  一般情况下，因素集中的各因素在综合评价中所起的作用是不相同的，综合评价结果不仅与各因素的评价有关，而且在很大程度上还依赖于各因素对综合评价所起的作用，这就需要确定一个各因素之间的权重分配，它是U上的一个模糊向量，记为 $A=[a_1,a_2,\cdots ,a_n]$。

其中：ai 为第 i 个因素的权重，且满足 ∑ai=1。如果不满足加和为1，那么可以在此处实现归一化，也可在最终结果处归一化。

假设说，此处已经确定了 各因素的权重 A = [0.25，0.2，0.25，0.3]

  确定权重的方法有很多，如：Delphi法（专家调查法）、加权平均法、众人评估法。但是建议：当没有数据的时候可采取层次分析法，有数据的时候可采取熵权法。 具体实现请查看以下两篇文章：
数学建模 | 层次分析法（AHP）
数学建模 | 熵权法（客观赋权法）

---

第四步：确定模糊综合评判矩阵，对每个元素 ui 做出评价

(注意：这里演示的是模糊统计法，并且这里的评定员工只有一位)

1. u1（工作业绩）比如由群众评议打分来确定：
   R1 = [0.1，0.5，0.4，0，0] 。这个式子表示，参与打分的群众中，有10%的人认为政治表现优秀，50%的人认为政治表现良好，40%的人认为政治表现一般，认为政治表现较差或差的人为0。用同样方法对其他因素进行评价。
2. u2（工作态度），u3（沟通能力），由部门领导打分来确定:
   R2 = [ 0.2，0.5 ，0.2，0.1，0 ]，R3= [ 0.2，0.5，0.3，0，0 ]。
3. u4（政治表现）由单位考核组成员打分来确定:
   R4= [ 0.2，0.6，0.2，0，0]。

以 Ri 为第 i 行构成评价矩阵：

注意：

1. rij 与隶属度的计算方式有关，方法选取的不同隶属度可能有差异
2. 0 ≤ rij ≤ 1
3. 大小为 n × m，其中 n 是因素指标数目，m 是评语数目

---

第五步：模糊综合评判

进行矩阵合成运算：

最终得出结果：B = [0.175，0.53，0.275，0.02，0]。
大小为 1 × m，其 bi 表示意义为：要评价对象对评语 i 的隶属度。
如：0.175 代表员工表现优秀的隶属度为 0.175，或者说优秀占比17.5%（归一化），员工表现良好占比53%，以此类推。

取数值最大的评语作为综合评判结果，则该员工的评判结果为“良好”。

---

例2：空气质量

下表给出了大气污染物评价标准，
今测得某日某地表中这些污染物日均浓度依次为：(0.07，0.20，0.123，5.00，0.08，0.14)
各污染物权重确定如下：(0.1，0.2，0.3，0.3，0.05，0.05)
试评价当天空气质量等级。

表  大气污染物评价标准  mg/m3

解：
第一步：取因素集： U = {SO2，TSP，NOx，CO，PM1，O3}
第二步：取评语集： V = {I级，Ⅱ级，Ⅲ级，Ⅳ级}
第三步：确定各因素权重：A = [ 0.1，0.2，0.3，0.3，0.05，0.05]
第四步：确定模糊综合评判矩阵。
（与上一题相比，这里给了实际的空气污染的等级数据计算隶属度，因此选用指派法。）

  首先，需要构造隶属函数
   其中I级为偏小型，Ⅱ级和Ⅲ级为中间型，Ⅳ级为偏大型。

污染物i对空气质量各等级的隶属函数(梯形分布)

  其次，代入数据求解模糊综合评判矩阵

  各种污染物的浓度分别为 ( 0.07，0.20，0.123，5.00，0.08，0.14)，拿 SO2 为 0.07mg/m3 举例:

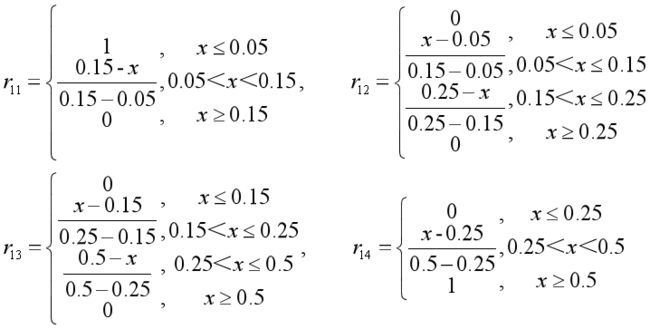
  则 :

  将其结果填入矩阵，以此类推，最终的模糊综合评判矩阵为：

第五步：综合评判

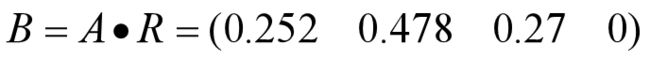
最终结果得出，空气质量为二级（二级的隶属度最高）！

---

重要扩展：

  上面的空气质量例题因为其每个污染物指标都趋于一个方向，即污染物含量越少所对应的空质量越好（这里可以理解为 TOPSIS 中的极小型指标），那么可以用一组隶属函数。
  但如果说指标含有不同类型的指标，如：既含有极大型指标也含有极小型指标，那么这里就需要注意了，一种方案可采取建立不同隶属函数分别对应相应类型的指标，另一种方案可以采取正向化都变成极大型指标。

  注意：上文提到的极大型（极小型）指标，和模糊集合的三类（偏小型、中间型、偏大型）是两种概念。极大型（极小型）指标强调的是指标本身对于评语或者方案的好坏（越多越好，或者越少越好），而模糊集合的三类（偏小型、中间型、偏大型）强调的是指标数值的趋向程度。

那么我们拿一道例题说明：

---

  由题目我们可以明确：评语集变成5种方案，因素集的五种因素，可采矿量、净现值为极大型指标，基建投资、采矿成本一级不稳定费用是极小型指标，因此就需要对其进行一些处理，直接看答案是怎么处理的吧~

  答案将 基建投资、不稳定费用 正向化成极大型指标，对于极小型指标 采矿成本 单独建立隶属函数进行求值，当然这也可以做和 基建投资、不稳定费用 一样的正向化处理。

  这里我们需要注意：当隶属函数求值只用梯形分布最终的隶属度和为1，用其他方法求隶属度会使得最终的隶属度和不为1，但不影响最终的评判效果。另外一点，这里这道题目对于基建投资、不稳定费用隶属函数的求法是采取的第二种：借助已有的客观尺度。

---

3. 多级模糊综合评价

  一级模糊综合评价是多级模糊综合评价的基础。它是将一级模糊评价因素集指标的相关性指标进行 统一综合，因为上文讲过一级模糊评价的指标之间是相关性不强的，那么这样相关性指标在只考虑这一种因素的情况下是不相关的，即相对不相关。然后对每个相关性指标进行综合，求得只看这一组指标对于评语集的隶属度，此方法进行类推，最后在综合。

---

例：评价学⽣的表现并作为奖学金的评判标准。
因素集 U = { 专业课成绩、非专业课成绩、国家竞赛成绩、省级竞赛成绩、校级竞赛成绩、国家级奖项、省级奖项、校级奖项、志愿服务}
评语集 V = {一等，二等，无奖学金}

假设我们现在权重的分配如上图所示，那么先对 u(1) 进行一级模糊评判，
假设 R1 =[0.8 0.2 0; 0.7 0.3 0]，进行综合评判：B1 = A1·R1 = [0.76 0.24 0]。
结果表明只看学习成绩76%的人认为该名同学可以获得一等，24%的人认为该名同学可以获得二等。

以此类推，我们分别获得了只看竞赛成绩、只看个人荣誉、只看志愿服务的该名同学获得奖学金的隶属度。
那么构造最终的模糊综合评判矩阵：

在进行最终的综合评判：B = A·R =[0.439，0.297，0.264]，所以最终这名学生获得一等奖学金。

---

五、模型总结

1. 隶属函数有三种确定方法，要根据实际情况来选择使用。
2. 极大型（极小型）指标，和模糊集合的三类（偏小型、中间型、偏大型）是两种概念，注意区分。
3. 模糊综合评价的因素指标是相关性不强的，如果有相关项较强的需要进行多级模糊综合评价，级数一般不超过3层。
4. 隶属函数的指派法，分布的选取含有一定的主观性，应有必要的文字说明。

---

本文借鉴了数学建模清风老师的课件与思路，如果大家发现文章中有不正确的地方，欢迎大家在评论区留言哦~