算法--数N的组合方式,由给定的数组元素进行组合--已改进1版

这是百度面试一道算法题.当时没答上来,主要是思考方式不对.

想算法问题的时候一定要按照电脑的逻辑来,不能按照人脑的逻辑顺序来.(主要还是程序练得不够)

举个例子:a+b 的逆波兰式为ab+, 这很简单,但是在思考的时候不要先想把+号拿出来,放到后面,要思考,从左到右电脑如何处理才能得出ab+.这样才能写出程序算法.而不是人脑算法.

 

当时的题目是这样的.

人民币有 1元 2元 5元 10元 20元 50 元 100元  这几种币值.

问:给定200元,求出有多少种币值组合方式.  币种可重复,比如,200张1元的算一种方式. 

 

题目很简单,做起来难.程序逻辑就是

int a[] = { a1, a2, a3, a4, a5...}

n = N

用a数组中各元素相加得N的情况有哪些?

 

有一天做班车上想了一下,来了灵感.....但是对于像n = 3,  1+2 和2 +1这种重复的方式还不能去重.因为我这个方法非常暴力.而且这个方法不太好,当N比较大时,就需要运行很长时间.(代码已改进,可以去重了)

主要逻辑是:

　　将N依次减去a[]中各值,得0,表示是一种方式;大于0,递归n = n-a[i];小于0,返回.

我以n = 3 a[] = {1,2}画了个图,助以理解.红色为组合序列,存入链表. 大括号{前的-为减去.

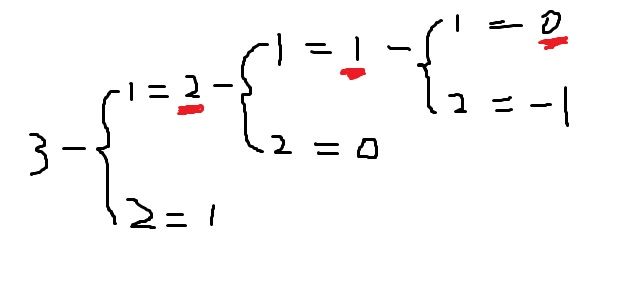
#include <stdio.h>

#include <time.h> 

#include "线性表的链式存储.c"



int a[] = {1,2,5,10,20,50,100};

struct sNode *result;

int len =0;

int counts =0; 



elemType getHead(struct sNode *result)

{

    if(result == NULL) return -1; 

    else{

        while(result->next != NULL)

        {

            result = result->next;    

        }

        return result->data;    

    }  

} 



int sumList(struct sNode *result)

{

    int sum = 0; 

    if(result == NULL) return 0; 

    while(result->next != NULL)

    {

        sum = sum + result->data; 

        result = result->next;   

    }

    sum = sum + result->data;

    return sum; 

} 

int compute(int n)

{

    int i = 0;

    

    for(i = 0; i < len; i++)

    {/* 

         travelList(result); printf("\n");

        printf("getHead(result) = %d  a[%d] = %d \t\n",getHead(result),i,a[i]); 

       */   

        if(getHead(result) != -1 &&  getHead(result) > a[i])    /*若果要放入的数比前面的数小,则跳到小一个.用于去除重复的组合方式. 比如n=3,,对于2,1这种,1比2小就不考虑了*/

        {   

         /*   printf("下一个a[i]"); */ 

            continue;

        } 

        if(n - a[i] < 0)

        {

            return 0;

        }

        if(n - a[i] == 0) 

        {        

            counts++;     

            printf("   %d     =    ",sumList(result) + a[i]); 

            travelList(result);

            printf("%d\n",a[i]); 

            return 0; 

        }

                     

        insertLastList(&result, a[i]);

        compute(n-a[i]);   

        deleteLastList(&result); 

    }         

} 



int main()

{

    double cost_time;

    clock_t start,end;

     

    initList(&result);

    len = sizeof(a)/4;

    int i; 

    int n = 200; 

    

    printf("n = %d   a[] = ",n);

    for(i = 0; i< len; i++)

    {

        printf("%d ",a[i]); 

    }

    printf("\n*****************组合方式为*****************\n");

    printf("链表总和     链表中各元素\n"); 

    

    start=clock(); 

    compute(n);

    end=clock();

    

    cost_time=(double)(end-start)/CLOCKS_PER_SEC; 

    printf("\n一共有 %d 种组合方式...\n",counts); 

    printf("所用时间: %f\n",cost_time); 

    

    system("pause");   

    return 0;    

}

 

******************************************************

运行结果: 只截取了部分.运行时间不准确,看你机器当前在干什么了.第一次运行160秒.我估计什么也不干,差不多在2分半.

***************************************************

 

   200     =    10 10 10 10 20 20 20 20 20 20 20 20

   200     =    10 10 10 10 20 20 20 50 50

   200     =    10 10 10 10 20 20 20 100

   200     =    10 10 10 20 20 20 20 20 20 50

   200     =    10 10 10 20 50 50 50

   200     =    10 10 10 20 50 100

   200     =    10 10 20 20 20 20 20 20 20 20 20

   200     =    10 10 20 20 20 20 50 50

   200     =    10 10 20 20 20 20 100

   200     =    10 20 20 20 20 20 20 20 50

   200     =    10 20 20 50 50 50

   200     =    10 20 20 50 100

   200     =    20 20 20 20 20 20 20 20 20 20

   200     =    20 20 20 20 20 50 50

   200     =    20 20 20 20 20 100

   200     =    50 50 50 50

   200     =    50 50 100

   200     =    100 100



一共有 73681 种组合方式...

所用时间: 301.283000

请按任意键继续. . .

 

网络上其他牛人给出的算法.数学方法. 

 http://topic.csdn.net/u/20070202/23/65f55fbf-a37c-4e42-82b9-22ebdd573523.html