（11）pytorch之损失函数

一、损失函数（衡量模型输出与真实标签的差异）

1.损失函数，代价函数，目标函数的区别：
损失函数：一个样本的差异

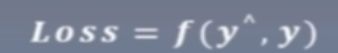
代价函数： 所有样本损失的均值

目标函数：obj=Cost+Regulaization（正则项：防止过拟合）

2 常用损失函数

a：nn.CrossEntropyLoss:nn.LogSoftmax()（数据归一化）与nn.NLLLoss()结合，进行交叉熵计算。

主要参数 weight：各类别的loss设置权值，每个类别的权值
ignore_index:忽略某个类别，不计算loss
reduction：计算模式（none逐个计算/sum所有元素求和返回标量/mean加权平均返回标量）

inputs=t.tensor([[1,2],[1,3],[1,3]],dtype=t.float)
target=t.tensor([0,1,1],dtype=t.long)
loss_f_none=nn.CrossEntropyLoss(weight=None,reduction="none")
loss_f_sum=nn.CrossEntropyLoss(weight=None,reduction="sum")
loss_f_mean=nn.CrossEntropyLoss(weight=None,reduction="mean")
loss_none=loss_f_none(inputs,target)
loss_sum=loss_f_sum(inputs,target)
loss_mean=loss_f_mean(inputs,target)
print("Cross Entropy Loss:\n",loss_none,loss_sum,loss_mean)

b:nn.NLLLoss:实现负对数似然函数中的负号功能（只实现了负号功能）

主要参数同上

c:nn.BCELoss():二分类交叉熵，注意输入值取值在0,1

主要参数同上

d:nn.BCEwithLogitsLoss:结合sigmoid与二分类交叉熵（模型中不用再加sigmoid了）

主要参数：同上，多了个pos_weight:正样本的权值

e：回归常用损失函数：nn.L1Loss(计算output与target之差的绝对值)和nn.MSELoss(计算outputs和target之差的平方)taget与output一一对应（形状也相同）
SmoothL1Loss(平滑的L1损失函数，当差距过大时用不同的公式，最后取平均，这里的x和y就是output和target)


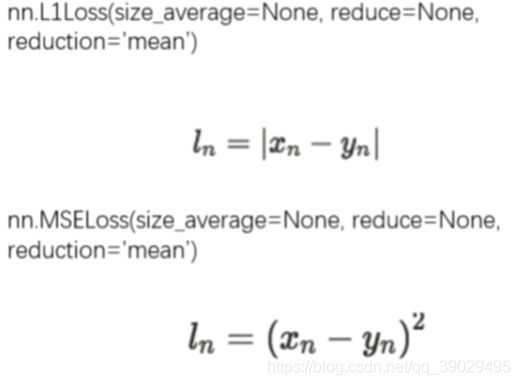
f:poissonNLLLoss:泊松分布的负对数似然函数，分类为泊松分布时使用

主要参数：log_input:输入是否为对数形式，决定计算公式，如上面
full:计算所有loss，默认为False
eps：修正项，避免log（input)为nan，避免当input为0的时候报错，然式子+eps（很小不会影响正确性）

g:nn.KLDivLoss计算KL散度（相对熵），下面的式子为pytorch中的实际公式，上面的为理论上的（注意，我们的inputs需要通过nn.logsoftmax()计算log_probabilities）

参数：reduction多了一个batchmean（batchsize维度求平均值）

h:nn.MarginRankingLoss:计算两个向量之间的相似度，用于排序任务，返回一个n*n（第一组中每个元素与第二组中的所有元素都进行loss计算）的loss矩阵



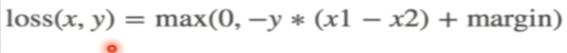
主要参数：margin：边界值，x1与x2之间的差异值，（y取值1/-1，表示我们希望哪个大一些）
eduction：同上
loss_f_none=nn.MarginRankingLoss(margin=0,reduction=“none”)
loss=loss_f_none(x1,x2,target)target为y值

i:nn.MultiLabelMarginLoss(多标签（不是多分类，是一个可能属于多个类别）)


eg：一个四分类任务，样本属于0和3类，则标签应该为[0,3,-1,-1]而非[1,0,0,1],那个where解释了为什么注意i≠y[j]即后面的x[i]为前面y[j]=-1对应的数据
含义：为了让标签神经元越来越明显，越来越接近1，这样才能减小loss
x=t.tensor([[0.1,0.2,0.4,0.8]])
y=t.tensor([[0,3,-1,-1]],dtype=t.long)
loss_f=nn.MultiLabelMarginLoss(reduction=“none”)
loss=loss_f(x,y)
print(loss)

j：nn.SoftMarginLoss(计算二分类的logistic损失)


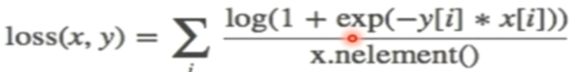
主要参数：reduction
nn.MultiLabelSoftMarginLoss(多标签版本)


参数多了个weight：各个类别的loss设置权值，这个的y为[1,0,0,1]了