损失函数汇总和Pytorch代码示例

一.交叉熵损失

1.交叉熵是一个信息论中的概念，它原来是用来估算平均编码长度的。给定两个概率分布p和q，通过q来表示p的交叉熵为

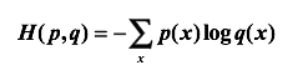
注意，交叉熵刻画的是两个概率分布之间的距离，或可以说它刻画的是通过概率分布q来表达概率分布p的困难程度，p代表正确答案，q代表的是预测值，交叉熵越小，两个概率的分布约接近

那么，在神经网络中怎样把前向传播得到的结果也变成概率分布呢？Softmax回归就是一个非常有用的方法。（所以面试官会经常问你，为什么交叉熵经常要和softmax或者Sigmoid一起使用？）
假设原始的神经网络的输出为，那么经过Softmax回归处理之后的输出为：

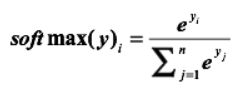
这样就会出现我们所要的概率

1.很多人都在问Softmax和Sigmoid到底有什么区别和联系？
(1)首先Sigmoid是基于单值进行映射，具体来说，就是你想要Sigmoid的一，二，三乃至高阶张量都不会彼此干扰，每个值都会对自己负责！eg: 可以用来二分类
(2)Softmax是基于整个维度上进行映射，具体来说，将你想要的一，二，三乃至高阶张量都会收到彼此的影响，每个值都会收到整体的影响！eg:可以进行多分类
(3)话不多说，咱们来看代码，从下面可以清晰的看出来Sigmoid中每个值是独立的，而Softmax会考虑你所选维度的整体值即和为1

tensor = torch.Tensor([1.0, -1, 0.1, -0.1])
print(torch.sigmoid(tensor))
print(torch.softmax(tensor,dim=0))

**在这交叉熵损失会分为二分类交叉熵和多分类交叉熵损失：
多分类交叉熵：在这路由于全部取最高概率则不会出现二分类交叉熵中的分类情况（0,1）

Pytorch实现：

torch.nn.CrossEntropyLoss(weight=None, ignore_index=-100, reduction='mean')

args：weight (Tensor, optional) – 自定义的每个类别的权重. 必须是一个长度为 C 的 Tensor，用来平衡分布不均的数据
ignore_index (int, optional) – 设置一个目标值, 该目标值会被忽略, 从而不会影响到 输入的梯度。
reduction-三个值，none: 不使用约简；mean:返回loss和的平均值； sum:返回loss的和。默认：mean

二分类交叉熵：

Pytorch实现：
（1）torch.nn.BCELoss(weight=None, reduction='mean')
（2）torch.nn.BCEWithLogitsLoss(weight=None, reduction='mean', pos_weight=None)

上述中（1）是你已经Sigmoid（2）是该损失函数帮你Sigmoid

二.均方差损失

均方差损失函数常用在最小二乘法中。它的思想是使得各个训练点到最优拟合线的距离最小（平方和最小）。均方差损失函数也是我们最常见的损失函数

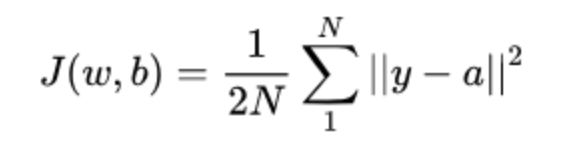
其中，a代表网络输出结果，之所以用2N是为了BP求导时和平方进行约分便于计算

Pytorch中的实现

torch.nn.MSELoss(reduction='mean')
args：reduction-三个值，none: 不使用约简；mean:返回loss和的平均值； sum:返回loss的和。默认：mean。

三.L1和Smooth-L1损失

对于目标检测中的回归问题，最初大多采用均方误差损失$||y-f(z)|{|}^2$ ，这样反向传播对w或者b求导时仍存在 $y-f(z)$ 。那么当预测值和目标值相差很大时，就容易造成梯度爆炸

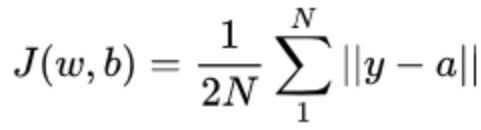
Pytorch中的实现：
torch.nn.L1Loss(reduction='mean')
平滑后的L1损失更加鲁棒
torch.nn.SmoothL1Loss(reduction='mean')

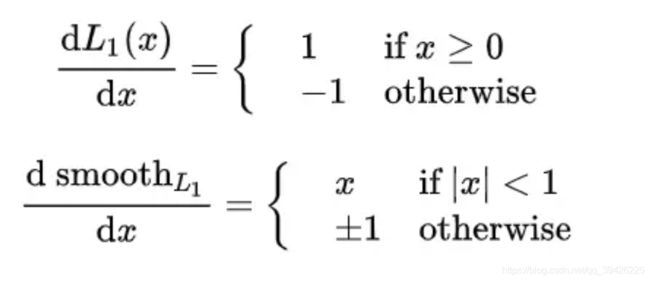
从上面可以看出平滑后的L1损失在梯度太大时会限制到(-1,1)即smooth L1 在 x 较小时，对 x 的梯度也会变小，而在 x 很大时，对 x 的梯度的绝对值达到上限 1，也不会太大以至于破坏网络参数。

四.KL 散度损失

计算 input 和 target 之间的 KL 散度。KL 散度可用于衡量不同的连续分布之间的距离, 在连续的输出分布的空间上(离散采样)上进行直接回归时 很有效.

Pytorch中：
torch.nn.KLDivLoss(reduction='mean')