高斯混合模型(GMM)学习笔记
专题:高斯混合模型
在实际应用中,kmeans的非概率性和它仅根据到簇中心点的距离来指派簇的特点将导致性能低下。
二高斯混合模型,可以看作是kmeans思想的一个扩展。
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import seaborn as sns
sns.set()
高斯混合模型(GMM)为什么会出现:k-means算法的缺陷
只要有简单的数据簇,kmeans算法就可以快速给这些簇作标记,标记结果和通过肉眼观察到的簇的结果十分接近:
#生成数据
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=400, centers=4,
cluster_std=0.60, random_state=0)
X = X[:,::-1]#交换列,方便画图
#用k-means标签画出数据
from sklearn.cluster import KMeans
kmeans = KMeans(4, random_state=0)
labels = kmeans.fit(X).predict(X)
plt.scatter(X[:,0],X[:,1], c=labels, s=40, cmap='viridis');
为了更明确的看出kmeans模型的计算法方法,可以用以下函数将这个聚类模型可视化:
from sklearn.cluster import KMeans
from scipy.spatial.distance import cdist
def plot_kmeans(kmeans, X, n_cluster=4, rseed=0, ax=None):
labels= kmeans.fit_predict(X)
#画出输入数据
ax = ax or plt.gca()
ax.axis('equal')
ax.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis', zorder=2)
#画出kmeans模型的表示
centers = kmeans.cluster_centers_
radii = [cdist(X[labels==i], [center]).max()
for i, center in enumerate(centers)]
for c, r in zip(centers, radii):
ax.add_patch(plt.Circle(c, r, fc='#CCCCCC', lw=3, alpha=0.5, zorder=1))
kmeans = KMeans(n_clusters=4, random_state=0)
plot_kmeans(kmeans,X)
kmeans有一个重要特征,它要求这些簇的模型必须是圆形:
kmeans算法没有内置的方法来实现椭圆形的簇。
因此,如果对同样的数据进行一些转换,簇的分配就会变得混乱
rng = np.random.RandomState(13)
X_stretched = np.dot(X, rng.randn(2, 2))
kmeans = KMeans(n_clusters=4, random_state=0)
plot_kmeans(kmeans, X_stretched)
一般化E-M:高斯混合模型
一个高斯混合模型(GMM)试图找到多维高斯概率分布的混合体,从而获得任意数据集最好的模型。
在最简单的场景中,GMM可以用与kmeans相同的方式寻找类
GMM已经被GaussianMixture代替
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_components=4).fit(X)
labels = gmm.predict(X)
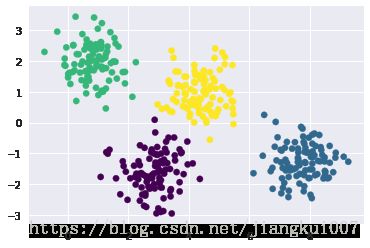
plt.scatter(X[:,0],X[:,1], c=labels, s=40, cmap='viridis');
由于GMM有一个隐含的概率模型,因此它也可能找到簇分配的概率结果——在scikitlearn中用predict_proba方法实现。
这个方法返回一个大小为[n_samples, n_clusters]的矩阵,矩阵会给出任意点属于某个簇的概率:
probs = gmm.predict_proba(X)
print(probs[:5].round(3))
[[0.463 0.537 0. 0. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[0. 1. 0. 0. ]
[0. 0. 0. 1. ]]
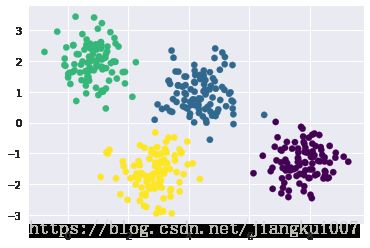
我们可以将这个不确定性可视化,用每个点的大小体现预测的不确定性。
size = 50 * probs.max(1) ** 2 # 平方强调差异
plt.scatter(X[:,0],X[:,1], c=labels, s=size, cmap='viridis');
GMM本质上和kmeans模型非常类似,它们都是用了期望最大化方法,具体实现如下:
(1)选择初始簇的中心位置和形状。
(2)重复直至收敛
a.期望步骤(expectation):为每个点找到对应的每个簇的概率作为权重。
b.最大化步骤(maximization):更新每个簇的位置,将其标准化,并且基于所有数据点的权重来确定形状。
from matplotlib.patches import Ellipse
def draw_ellipse(position, covariance, ax=None, **kwargs):
"""用给定的位置和协方差画一个椭圆"""
ax = ax or plt.gca()
#将协方差转换成主轴
if covariance.shape == (2,2):
U, s, Vt = np.linalg.svd(covariance)
angle = np.degrees(np.arctan2(U[1,0], U[0,0]))
width, height = 2 * np.sqrt(s)
else:
angle = 0
width, height = 2 * np.sqrt(covariance)
#画出椭圆
for nsig in range(1,4):
ax.add_patch(Ellipse(position, nsig * width, nsig * height, angle, **kwargs))