机器学习-白板推导-系列(十一)笔记:高斯混合模型
文章目录
- 0 笔记说明
- 1 模型介绍
- 2 极大似然
- 3 EM求解
-
- 3.1 E-Step
- 3.2 M-Step
0 笔记说明
来源于【机器学习】【白板推导系列】【合集 1~23】,我在学习时会跟着up主一起在纸上推导,博客内容为对笔记的二次书面整理,根据自身学习需要,我可能会增加必要内容。
注意:本笔记主要是为了方便自己日后复习学习,而且确实是本人亲手一个字一个公式手打,如果遇到复杂公式,由于未学习LaTeX,我会上传手写图片代替(手机相机可能会拍的不太清楚,但是我会尽可能使内容完整可见),因此我将博客标记为【原创】,若您觉得不妥可以私信我,我会根据您的回复判断是否将博客设置为仅自己可见或其他,谢谢!
本博客为(系列十一)的笔记,对应的视频是:【(系列十一) 高斯混合模型1-模型介绍】、【(系列十一) 高斯混合模型2-极大似然】、【(系列十一) 高斯混合模型3-EM求解-E-Step】、【(系列十一) 高斯混合模型4-EM求解-M-Step】。
下面开始即为正文。
1 模型介绍
高斯混合模型(Gaussian Mixture Model,GMM)指的是多个高斯分布函数的线性组合,是一种生成模型。
从几何角度来看:高斯混合模型是多个高斯分布函数的叠加。设共有K个高斯分布,对于第k个高斯分布来说,其形式为N(μk,Σk),其中k=1,2,…,K,则高斯混合模型的的PDF(probability density function,概率密度函数)即P(X)如下图,其中图中的αk是第k个高斯分布的权重:
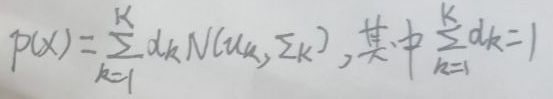
从混合模型的角度来看:假设有N个样本实例,为X=(x1,x2,…,xN)。引入隐变量Z=(z1,z2,…,zN),对于每个样本xi,都对应于一个zi,用于代表xi是属于K个高斯分布中的哪一个,其中i=1,2,…,N。假设Ck是第k个高斯分布,其中k=1,2,…,K,当zi=Ck时,概率P(zi=Ck)=pk,其中i=1,2,…,N,若pm最大则代表xi属于第m个高斯分布Cm。如下图为zi的分布,可知zi为离散型随机变量,其中i=1,2,…,N。对于zi,其概率分布的参数为p=(p1,p2,…,pK):

X的概率密度函数P(X)可写为(与本节第一张图不谋而合):

高斯混合模型的概率图如下:

上图右下角的N代表有N个样本实例。
2 极大似然
假设有N个样本实例为X=(x1,x2,…,xN),X称为观测数据,其中当i≠j时有xi与xj相互独立,引入隐变量Z=(z1,z2,…,zN)。(X,Z)称为完整数据,有x|z=Ck~N(μk,Σk),即:

高斯混合模型的参数θ={(p1,p2,…,pK),(μ1,μ2,…,μK),(Σ1,Σ2,…,ΣK)}。如果用极大似然估计求θ会怎么样呢?如下:
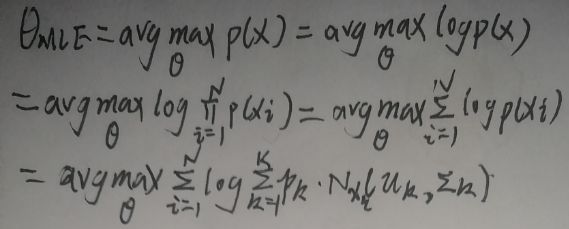
从最后一行观察可知,目标函数中对数内是连加形式,因此难以或者无法求解。
下面使用EM算法求解参数θ,关于EM算法,可以看这里。
3 EM求解
3.1 E-Step
θ(t+1)为:

记Q(θ,θ(t))为上图的目标函数,则可以对Q(θ,θ(t))进行整理:

将上图最后一行公式的第一项展开:

对框住的部分有:

即上上一张图最后框住的部分等于1,则上上上一张图最后一行公式的第一项展开为:

则Q(θ,θ(t))为:

又因为:

所以Q(θ,θ(t))为:

将框住的部分写为p(zi|xi,θ(t)),然后继续对Q(θ,θ(t))继续化简:
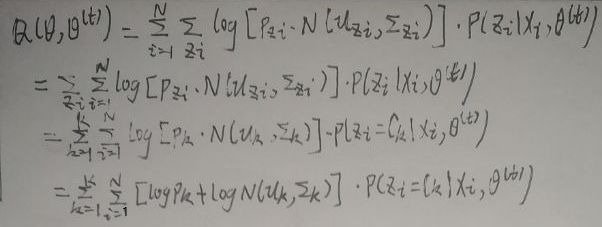
于是θ(t+1)为:

3.2 M-Step
高斯混合模型的参数θ={(p1,p2,…,pK),(μ1,μ2,…,μK),(Σ1,Σ2,…,ΣK)},即有三组参数:
(1)p=(p1,p2,…,pK);
(2)μ=(μ1,μ2,…,μK);
(3)Σ=(Σ1,Σ2,…,ΣK)。
下面只示范性地求p(t+1)=(p1(t+1),p2(t+1),…,pK(t+1)),对pk(t+1),其中k=1,2,…,K,有:

其中:

这是一个带约束的优化问题,下面使用拉格朗日乘数法解决,先构造拉格朗日函数L(pk,λ)为:
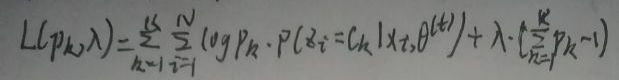
对L(pk,λ)关于pk求偏导,并令偏导数等于0:

上图最后框住的两部分都等于1,于是有:

所以λ=-N,其中N是样本实例的数量。将λ=-N代入下式:

得:
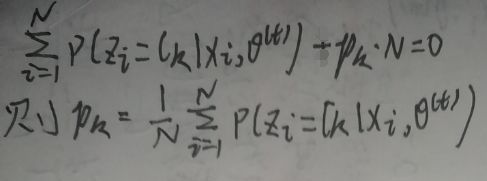
最后有pk(t+1)如下,其中k=1,2,…,K:

求解p(t+1)结束,其中p(t+1)=(p1(t+1),p2(t+1),…,pK(t+1))。
END