时序分析(4) -- 移动平均模型(MA)

时序分析(4)

移动平均模型(MA)

    上一篇文章我们探讨了采用AR模型对时序数据进行建模，总的看来AR模型对金融序列建模并不是很理想。这一节我们主要讨论时序数据移动平均模型。
    首先我们介绍MA模型的基本概念：

Moving Average Models - MA(q)

    移动平均模型MA(q)其实和自回归模型有相似之处，不同之处在于移动平均是以过去的残差项也就是白噪声来做线性组合，而AR模型是以过去的观察值来做线性组合。MA的出发点是通过组合残差项来观察残差的振动.
    MA(q)模型定义如下：
如果一个单变量时序数据$\{y_t;t=1,2,...\}$,
$$y_t={\omega }_t+{\beta }_1{\omega }_{t-1}+...+{\beta }_p{\omega }_{t-p}$$

$$={\omega }_t+\sum _{t=1}^p{\beta }_i{\omega }_{t-i}$$

导入python包和数据

与前面文章中相同

模拟MA(1)过程

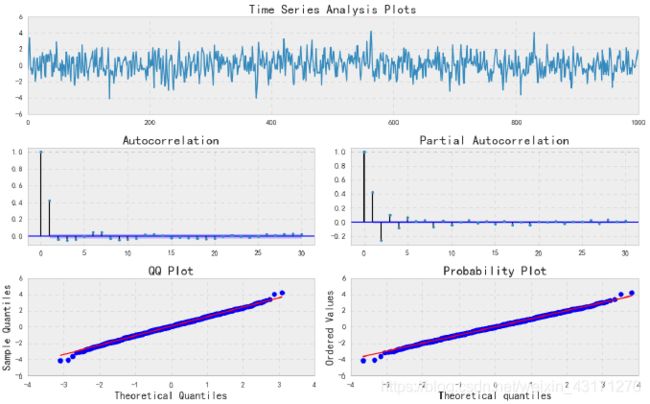
下面我们以β = 0.6来模拟一个MA(1)过程

# Simulate an MA(1) process
n = int(1000)
# set the AR(p) alphas equal to 0
alphas = np.array([0.])
betas = np.array([0.6])
# add zero-lag and negate alphas
ar = np.r_[1, -alphas]
ma = np.r_[1, betas]
ma1 = smt.arma_generate_sample(ar=ar, ma=ma, nsample=n)
_ = tsplot(ma1, lags=30)

现在我们对此模拟数据用MA(3)进行建模

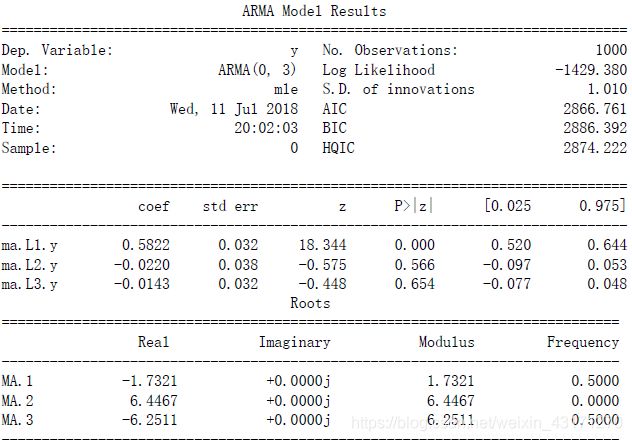
mdl_ma_sim = smt.ARMA(ma1, order=(0, 3)).fit(
                      maxlag=max_lag, method='mle', trend='nc')
print(mdl_ma_sim.summary())

• 国内股票收益率
  以MA建模，阶数设为3
  优化目标为Max Likelihood Estimation.

Y = indexs_logret['国内股票']
max_lag = 30
mdl_ma_gg = smt.ARMA(Y, order=(0, 3)).fit(
                     maxlag=max_lag, method='mle', trend='nc')
print(mdl_ma_gg.summary())
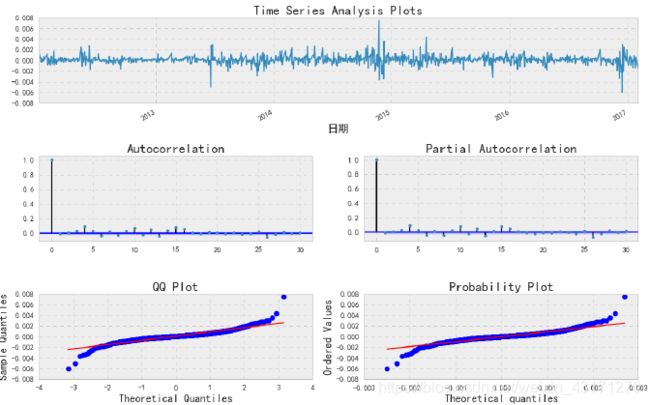
_ = tsplot(mdl_ma_gg.resid, lags=max_lag)

从拟合结果上看，只有一阶系数存在显著性。

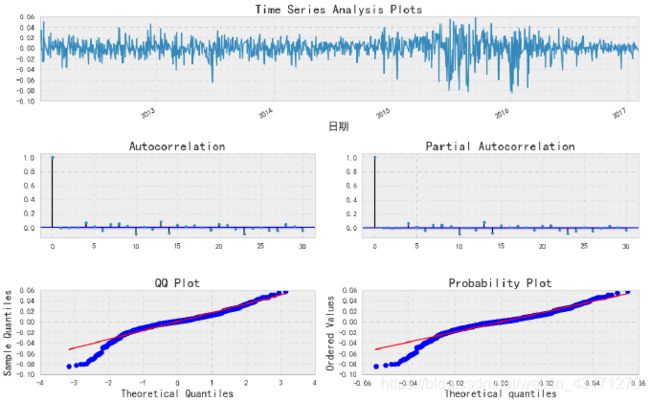
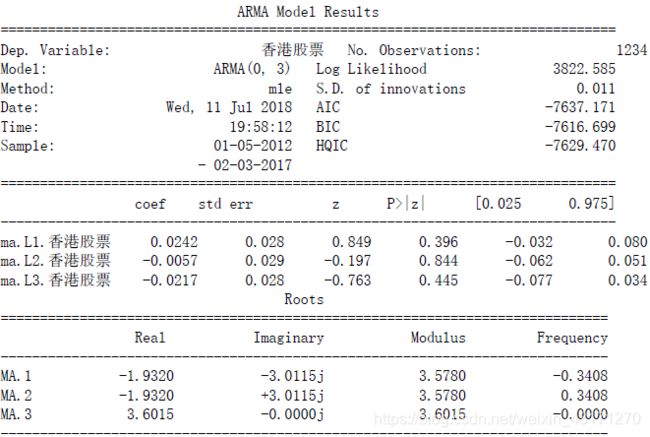
• 香港股票收益率
  以MA建模，阶数设为3

Y = indexs_logret['香港股票']
max_lag = 30
mdl_ma_gg = smt.ARMA(Y, order=(0, 3)).fit(
                     maxlag=max_lag, method='mle', trend='nc')
print(mdl_ma_gg.summary())
_ = tsplot(mdl_ma_gg.resid, lags=max_lag)

从第一阶到三阶系数都不存在显著性

• 国内债劵收益率
  以MA建模，阶数设为3
  优化目标为Max Likelihood Estimation.

Y = indexs_logret['国内债券']
max_lag = 30
mdl_ma_gg = smt.ARMA(Y, order=(0, 3)).fit(
                     maxlag=max_lag, method='mle', trend='nc')
print(mdl_ma_gg.summary())
_ = tsplot(mdl_ma_gg.resid, lags=max_lag)

总结

    本文展示了采用Python语言为四个指数时序数据进行移动平均建模，介绍了MA模型等相关概念。