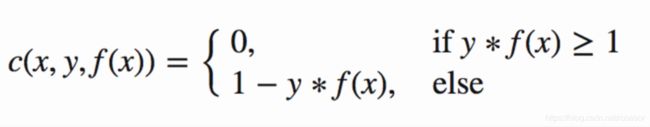MachineLearning学习——0215——逻辑回归、朴素贝叶斯分类、K最近邻
参考:https://github.com/apachecn/vt-cs4624-pyml-zh/blob/master/docs/12.md
逻辑回归
概念:一种二分类方法。目的是将输入映射到sigmoid函数上,进行二分类。
原理:
β值是权重,x 值是变量输入。 该公式给出了输入属于 B 类的可能性P(B) 。
特点:与线性回归相比,不需要设置先验类别阈值。能给出预测准确的概率。
但是由于预测值是连续的,当prob~=0.5时,两个类别的预测概率相近。(class0:0.46 class1:0.54)
*tips:多分类情况,用多项式逻辑回归。逻辑回归实践代码
具体的fit过程底层实现还得学习
朴素贝叶斯分类
背景:将输入分类为某个预先存在的类。即已知输入属于已知类中的一种,预测它是哪类。
原理:
- 已知存在2个类 Class1 and Class2,每类3个特征 如 大小,重量,颜色。
- 待分类输入 Input 1个,也包含上面三个特征 如 大小,重量,颜色。
- 如果 Input 和 Class1 有两个特征相同(Y1=X1,Y2=X2,Y3≠X3),则P(1)=2/3。与所有类相比,最后找出最大的概率
- 对比Input和Class的大小,重量,颜色。相同特征更多的,即同类。(os:好像猜父子,长得像的就同类)
为什么是朴素bys:
先说什么是贝叶斯,学过概率论的都知道:
![]()
朴素就是A与B相互独立。
用于朴素贝叶斯分类的常见模型:
| 模型 | 适用数据类型 | 适用情况 |
| 高斯 | 连续 | 不需要计算特征频率且包含十进制值时 |
| 多项式 | 离散 | 需要计算频率 |
| 伯努利 | 离散 | 判断特征是否发生(出现) |
都是概念性描述,模型的调用都封装好了,缺乏底层实现的讲解。
决策树
背景:使我们能够根据先前的数据进行预测
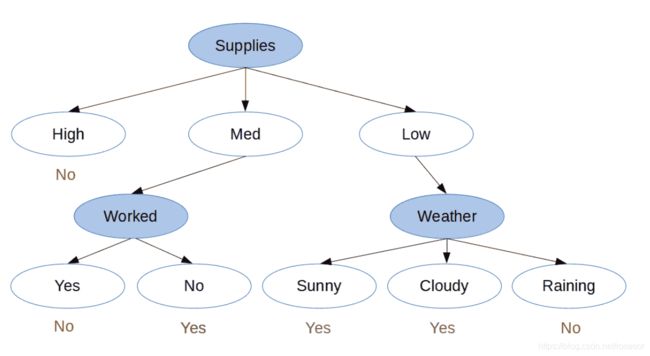
原理:不多bb,直接上图,和创建决策树的代码
图1左边的是条件,右边的是结果。图2是预测过程。
个人估计,每个预测值后面还有次数和概率,如Supplies(H) 10Times —>No, 8times,80%; —>Yes,2times,20%。
特点:
- 易于创建,可视化和解释
- 较大的数据集对树的创建过程的影响将小于其他分类器
- 新数据点的分类也可以对数地执行
创建原理:
通过称为归纳的拆分过程创建的,它决定何时拆分节点。使用贪婪算法,计算每次拆分的最低成本,确定拆分的最佳属性。
- 从根开始,我们为每个属性创建一个拆分。
- 对于每个创建的拆分,请计算拆分成本。
- 选择成本最低的拆分。
- 递归到子树,然后从步骤 1 继续。
拆分成本由成本函数决定。对于只有答案没有值的决策树,使用基尼不纯度计算信息增益。
决策树节点修剪:
原因:是数据集过大,产生决策树的节点过多。可能导致节点可用性低 or 过拟合。
方法:修剪涉及计算每个结束子树(叶节点及其父节点)的信息增益(详见原文),然后删除信息增益最小的子树。
k 最近邻
介绍:K近邻(KNN)是机器学习的基本分类器。分类器采用已标注的数据集,尝试将新数据点标记到已知数据的其中一类中。新数据与已知数据之间存在“距离关系”,距离比较近的可称为邻居。而多少算近,最远距离由K决定。在距离K内,其邻居多属哪类,就是新数据所属的类别。
距离计算模型:
- 欧几里得距离,即直线距离。在数据尺寸小、或点数小时效果好。点数过多时,表现下降。
- K-D树,也是欧式距离,但不用计算所有的。树中每个节点储存一个超平面,用于分割整个空间。若当前节点划分维度为d,左边空间的值小于d维所在的坐标(一般用中值),右边空间的数据d维所在的坐标。划分一次后,继续划分左右空间,不断切割至没有左子树。概念参考网站1,网站2。特点是 所有叶子节点到根节点的距离近似相等。但一个平衡的k-d tree对最近邻搜索、空间搜索等应用场景并非是最优的。
小总结:
- KNN 的不同方法只会影响表现,而不会影响输出
- 当点的尺寸或点数较小时,最好使用暴力法
- 当您拥有更大的数据集时,K-D 树方法是最好的
- SKLearn KNN 分类器具有一种自动方法,该方法可以根据所训练的数据来决定使用哪种方法。
选择 k 的值将大大改变数据的分类方式。 较高的 k 值将忽略数据的异常值,而较低的 k 值将赋予它们更大的权重。 如果 k 值太高,将无法对数据进行分类,因此 k 需要相对较小。
实践代码
SVM
介绍:与K最近邻类似,也是找超平面。区别是:1、一个SVM分类器只有一个超平面,只分两类。2、不需要计算数据之间的距离,只需要计算数据落在超平面哪里一侧。
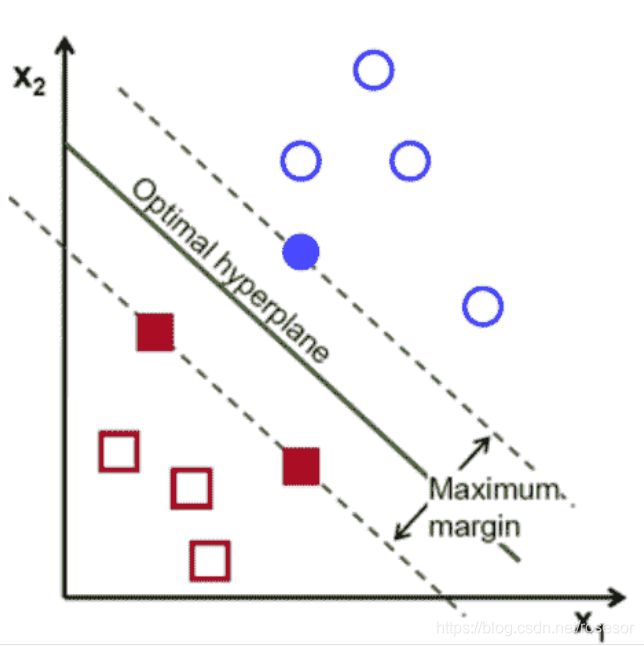
超平面:能将数据空间分割成两个断开部分的平面,维度取决于数据空间维度。1维空间的超平面是一个点,2维空间的超平面是一条线。但是能区分两类数据的超平面往往不止一个,如图1;SVM中,会选离两类数据都最远的超平面,称为最大边距,如图2。
图1
图2
最大边距:离超平面最近的数据点,是决定边距的关键,称为支持向量(support vector)。找到支持向量并最大化边距会涉及很多复杂的数学运算。 我们不会去讨论。原文建议,但我偏不哈哈哈
损失函数:从这个超级详细的宝藏博客学习到的
其中 f(x)= w*x,y=label。
当pred和label一样,则cost=0。否则cost = 1 - y*f(x)
梯度更新:
看完损失函数和svm代码的同学就会问了:为什么code里面的cost没有被用于w更新呢?
因为我们给cost加了正则化,求导后,直接用于更新w。
实际梯度更新公式如下:
![]()
代码实现如下:
w1 = w1 + alpha * (train_f1[count] * y_train[count] - 2 * 1 / epochs * w1) 其中t_f1*y_t就是cost的其中一部分。不过是求导后有变化。
*SVM分类忽略离群值,即粥里面的老鼠屎。
实践代码(need ):ctrl+F,搜索“Support Vector Machine(SVM) code in Python”跳转。
实践代码2(need ):超级底层实现
常用的三种类型的核:
- 线性核
实践代码有bug,gamma的值不能是0,应是1/n_feature。当有两个特征时,gamma=1/2=0.5svc = svm.SVC(kernel='linear', C=1,gamma=0)实际测试中,C几乎没有影响
- 多项式核
- 径向基函数(RBF)核
C是惩罚系数,即对误差的宽容度。c越高,说明越不能容忍出现误差,容易过拟合。C越小,容易欠拟合。C过大或过小,泛化能力变差
gamma越大,支持向量越少,gamma值越小,支持向量越多。支持向量的个数影响训练与预测的速度。
SVM 的优点:
- 有效地对高维空间进行分类
- 节省内存空间,因为它仅使用支持向量来创建最佳行。
- 数据点可分离的最佳分类器
与 SVM 的缺点:
- 有大量数据集时效果不佳,训练时间更长。
- 当类重叠时,即不可分离的数据点,表现会很差。
*一个博客的结论
此外,可以明确的两个结论是:
结论1:样本数目少于特征维度并不一定会导致过拟合,这可以参考余凯老师的这句评论:
“这不是原因啊,呵呵。用RBF kernel, 系统的dimension实际上不超过样本数,与特征维数没有一个trivial的关系。”
结论2:RBF核应该可以得到与线性核相近的效果(按照理论,RBF核可以模拟线性核),可能好于线性核,也可能差于,但是,不应该相差太多。
当然,很多问题中,比如维度过高,或者样本海量的情况下,大家更倾向于用线性核,因为效果相当,但是在速度和模型大小方面,线性核会有更好的表现。
老师木还有一句评论,可以加深初学者对SVM的理解:
“须知rbf实际是记忆了若干样例,在sv中各维权重重要性等同。线性核学出的权重是feature weighting作用或特征选择 。”