解题报告（十七）概率与期望（概率论）（ACM / OI）

繁凡出品的全新系列：解题报告系列 —— 超高质量算法题单，配套我写的超高质量题解和代码，题目难度不一定按照题号排序，我会在每道题后面加上题目难度指数（$1\sim 5$），以模板题难度 $1$ 为基准。

---

这样大家在学习算法的时候就可以执行这样的流程：

%
阅读我的【学习笔记】 / 【算法全家桶】学习算法 $\Rightarrow$ 阅读我的相应算法的【解题报告】获得高质量题单 $\Rightarrow$ 根据我的一句话题解的提示尝试自己解决问题 $\Rightarrow$ 点开我的详细题解链接学习巩固（好耶）

%
解题报告系列合集：【解题报告系列】超高质量题单 + 题解（ICPC / CCPC / NOIP / NOI / CF / AT / NC / P / BZOJ）

本期题单前置知识：【学习笔记】《概率与期望全家桶》（ACM / OI）概率与期望知识小结

概率

A. UVA11722 Joining with Friend（几何概型）

Problem

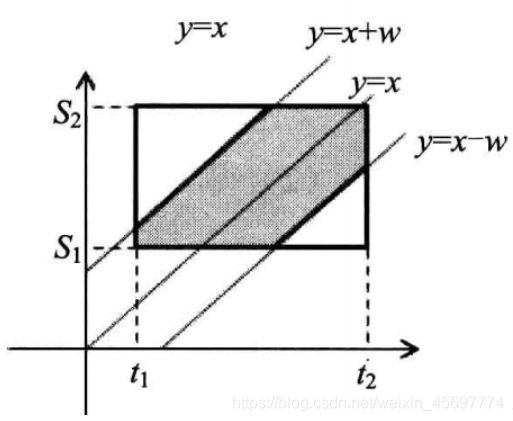
两人会面，第一个人去的时间在[t1, t2]中，第二个人去的时间在[s1, s2]中，两人会面成功的话，到达会面地点的时间差不能大于w，求两人成功会面的概率。

Solution

设 $a$ 在 $x$ 时间到达，$b$ 在 $y$ 时间到达，即 $|y-x|<=w$ 时可以碰面。即 $x-w<=y<=x+w$

显然答案就是总面积减去阴影面积。

我们设上面的白色面积为s1，中间阴影面积s2，下面白色面积为s3，则概率为 $\frac{s2}{s1+s2+s3}=\frac{(s2+s1)-s1}{s1+s2+s3}$

即我们可以直接计算直线 $y=x+w,y=x-w$ 切割的四边形上面交的面积，相减即可。

根据四边形形状长度的不同，直线 $y=x+w,y=x-w$ 与四边形的交一共有六种情况：

分类讨论即可。

Time

$O(1)$

Code

// Problem: UVA11722 Joining with Friend
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/UVA11722
// Memory Limit: 0 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include 

using namespace std;

const int N = 50007;

int n, m, t;
double s1, s2, t1, t2, w;
int kcase;

double get_area(double b)
{
     
	if(t1 + b >= s2) return 0;
	if(t2 + b <= s1) return (t2 - t1) * (s2 - s1);
	if(t1 + b >= s1 && t2 + b <= s2) return (t2 - t1) * (s2 - t2 - b + s2 - t1 - b) * 0.5;
	if(t1 + b >= s1 && t2 + b > s2) return (s2 - b - t1) * (s2 - b - t1) * 0.5;
	if(t1 + b <= s1 && t2 + b >= s2) return (s2 - s1) * (s1 - b - t1 + s2 - b - t1) * 0.5;
	if(t1 + b < s1 && t2 + b < s2 && t2 + b > s1) return (t2 - t1) * (s2 - s1) - (t2 + b - s1) * (t2 + b - s1) * 0.5;
	return 0;
}

void solve()
{
     
	scanf("%lf%lf%lf%lf%lf", &t1, &t2, &s1, &s2, &w);
	printf("Case #%d: ", ++ kcase);
	double tot = (t2 - t1) * (s2 - s1);
	double up = get_area(-w) - get_area(w);
	printf("%.8f\n", up / tot);
}

int main()
{
     
	scanf("%d", &t);
	while(t -- ) {
     
		solve();
	}
	return 0;
}

B. UVA11021 Tribles（概率DP）

Weblink

https://www.luogu.com.cn/problem/UVA11021

Problem

一开始有 $k$ 个麻球，所有麻球只能活 $1$ 天，死的时候有 $p_i$ 的概率产生 $i$ 只这种麻球（也只能活一天，$0\le i<n$），询问 $m$ 天内所有麻球都死的概率（包括m天前死亡的情况）

Solution

显然每个麻球是相互独立的，我们可以设 $f[i]$ 表示一个麻球第 $i$ 天以内死光的概率，则 $k$ 个麻球在第 $i$ 天内死亡的概率是 $f[i{]}^k$ 。

我们现在仅考虑一只麻球的情况，即该麻球第一天繁衍多少个，它们在接下来的 $i-1$ 天内死绝了。

根据全概率公式

$$P(A)=\sum _{i=1}^{n}P(A|B_i)\times P(B_i)$$

我们就可以设计转移方程：

$$f[i]=\sum _{j=0}^{n-1}p[j]f[i-1{]}^j$$

对于每一个麻球来说都有 $n$ 种选择。其中 $p_j(f_{i-1}{)}^j$ 的表示，生了 $j$ 个麻球，这些麻球在 $i-1$ 天内死光，即第一只 $a$ 及其后代需要在 $i$ 天内死光，那么第一只的直系后代 $b$ 及其后代需要在 $i-1$ 天内全部死光，因为第一只需要活一天，则 $b$ 的直系后代及其后代需要在 $i-2$天全部死光（$b$ 需要活了一天），即 $f[i]$由 $f[i-1]$ 转移过来，$f[i-1]$ 由 $f[i-2]$ 转移过来。

因为 $k$ 只麻球相互独立， 对于两个独立事件 $A,B$，$P(AB)=P(A)\times P(B)$

最后的答案就是 ${f[m]}^k$

Code

// Problem: UVA11021 Tribles
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/UVA11021
// Memory Limit: 0 MB
// Time Limit: 3000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include 

using namespace std;


const int N = 5007;

int n, m, k, t;
int kcase;
double p[N], f[N]; 	

void solve()
{
     
	scanf("%d%d%d", &n, &k, &m);
	for(int i = 0; i <= m; ++ i) f[i] = 0;

	for(int i = 0; i < n; ++ i) {
     
		scanf("%lf", &p[i]);
	}
	for(int i = 1; i <= m; ++ i) {
     
		for(int j = 0; j < n; ++ j) {
     
			f[i] += p[j] * pow(f[i - 1], j);
		}
	}
	printf("%.7f\n", pow(f[m], k));
}

int main()
{
     
	scanf("%d", &t);
	while(t -- ) {
     
		printf("Case #%d: ", ++ kcase);
		solve();
	}
	return 0;
}

C. 算概率（简单概率DP）

Weblink

https://ac.nowcoder.com/acm/contest/3003/C

Problem
Solution

显然概率DP，设 $fi,j$ 表示前 $i$ 道题里做对 $j$ 道的概率。转移时我们只需要考虑第 $j$ 道题是否做对即可。

转移方程为：

$$f_{i,j}=f_{i-1,j}\times (1-p_i)+f_{i-1,j-1}\times p_i$$

Time

$O(n^2)$

Code

// Problem: 算概率
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/3003/C
// Memory Limit: 524288 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include 

using namespace std;

const int N = 5007, mod = 1e9 + 7;

int p[N], f[N][N];
int n, m;

int main()
{
     
	scanf("%d", &n);
	for(int i = 1; i <= n; ++ i) {
     
		scanf("%d", &p[i]);
	}
	f[0][0] = 1;
	for(int i = 1; i <= n; ++ i) {
     
		f[i][0] = 1ll * f[i - 1][0] * (mod + 1 - p[i]) % mod;
		for(int j = 1; j <= i; ++ j) {
     
			f[i][j] = (1ll * f[i - 1][j] * (mod + 1 - p[i]) % mod + 1ll * f[i - 1][j - 1] * p[i] % mod) % mod;
		}
	}
	for(int i = 0; i <= n; ++ i) {
     
		printf("%d ", f[n][i]);
	}
	puts("");
	return 0;
}

D. UVA1636 决斗 Headshot

Problem

Solution

Code

// Problem: UVA1636 决斗 Headshot
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/UVA1636
// Memory Limit: 0 MB
// Time Limit: 3000 ms00
// 
// Powered by CP Editor (https://cpeditor.org)

#include 

using namespace std;

const int N = 50007;

int n, m;
string s;
int cnt00, cnt0, cnt1;

int main()
{
     
	while(cin >> s) {
     
		cnt00 = cnt0 = cnt1 = 0;
		int len = s.length();
		s += s[0];
		for(int i = 0; i < len; ++ i) {
     
			if(s[i] == '0') 
				cnt0 ++ ;
			if(s[i] == '0' && s[i + 1] == '0') 
				cnt00 ++ ;
		}
		int shoot = cnt00 * (len);
		int rotate = cnt0 * (cnt0);
		if(shoot == rotate) {
     
			puts("EQUAL");
		}
		else if(shoot < rotate) {
     
			puts("ROTATE");
		}
		else puts("SHOOT");
	}
	return 0;
}

E. UVA10491 奶牛和轿车 Cows and Cars

Problem

电视节目：你面前有 3 个门，其中两扇门后有奶牛，另 外一扇门后则藏着奖品——一辆豪华小轿车。在你选择一扇门之后， 门并不会立即打开。这时，主持人会给你个提示，具体方法是打开其 中一扇有奶牛的门（不会打开你已经选择那个门，即使里面是牛）。 接下来你有两种可能的决策：保持先前的选择，或者换成另外一扇未开的门。当然，你最终选择打开的那扇门后面的东西就归你了。 在这个例子里，你能得到轿车的概率是 2/3（难以置信吧！），方法是总是改变自己的选择。2/3 这个数字是这样得到的：如果开始选择了两个牛之一，你肯定能换到车前面的门，因为主持人已经让你看了另外一个牛；而如果开始你选择是车，就会换成剩下的牛并且失去大奖。由于你最初的选择是任意的，因此选错的概率是 2/3。也正是这 2/3 的情况让你能赢得大奖小轿车（另外 1/3 的情况你会从车转变为牛）。 现在把问题推广一下，假设有 a 头牛，b 辆车（门的总数是 a+b， 每个门后一头牛或一辆车），在最终选择前主持人会替你打开 c 个有 牛的门（$1\le a\le 10000,1\le b\le 10000,0\le c\le a$） ，输出 “总是换门” 策略下，赢得车的概率。

Solution

显然是一个古典概率，一共有两种互斥事件 $A$，$B$，所以分类讨论一下求和既是答案。$P(A\cup B)=P(A)+P(B)$。

Solution Source

Code

// Problem: UVA10491 奶牛和轿车 Cows and Cars
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/UVA10491
// Memory Limit: 0 MB
// Time Limit: 3000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include 

using namespace std;
const int N = 60007;

int n, m;
double a, b, c;

int main()
{
     
	while(scanf("%lf%lf%lf", &a, &b, &c) != EOF) {
     
		double ans = (a * b + b * (b - 1)) / ((a + b) * (a + b - c - 1));
		printf("%.5f\n", ans);
	}
}

F. UVA11181 条件概率 Probability|Given

// Problem: UVA11181 条件概率 Probability|Given
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/UVA11181
// Memory Limit: 0 MB
// Time Limit: 3000 ms
//
// Powered by CP Editor (https://cpeditor.org)

#include 

using namespace std;

const int N = 507;

int n, m, t, r;
double sum[N], tot;
double p[N];
bool vis[N];
int kcase;

void init()
{
     
	tot = 0;
	memset(vis, 0, sizeof vis);
	memset(sum, 0, sizeof sum);
}


//cnt第几个人num选了几个人
void dfs(int cnt, int num, double prob)
{
     
	if(num > r || n - cnt < r - num)
		return ;
	if(cnt == n) {
     
		tot += prob;
		for(int i = 0; i < n; ++ i) {
     
			if(vis[i])
				sum[i] += prob;
		}
		return ;
	}
	vis[cnt] = false;
	dfs(cnt + 1, num, prob * (1 - p[cnt]));
	vis[cnt] = true;
	dfs(cnt + 1, num + 1, prob * p[cnt]);

}

int main()
{
     
	while(scanf("%d%d", &n, &r) != EOF && n + r) {
     
		init();
		printf("Case %d:\n", ++ kcase);
		for(int i = 0; i < n; ++ i) {
     
			scanf("%lf", &p[i]);
		}
		dfs(0, 0, 1.0);
		for(int i = 0; i < n; ++ i) {
     
			printf("%.6f\n", sum[i] / tot);
		}
	}
	return 0;
}

G. UVALive6672 Bonus Cards

Weblink

Problem

Solution

Code

H. HDU 5985 Lucky Coins

I. HDU 5955 Guessing the Dice Roll

J. HDU 5819 Knights

期望

A. UVA12230 过河 Crossing Rivers（期望）

Problem

Solution

显然对于每条河来说，有两种情况极端情况：

最好的情况：到达河边时船刚好到，花费时间 $t=\frac{L}{v}$ 。

最坏的情况：到达河边时船刚好走，花费时间 $t=3\times \frac{L}{v}$ 。

由于船速度是匀速的，则根据期望的线性性质可得：每条河的平均过河时间 $t=\frac{\frac{L}{v}+3\times \frac{L}{v}}{2}=2\times \frac{L}{v}$ 。期望为 $E=t=2\times \frac{L}{v}$

显然总花费时间的期望为每条河的期望之和。

Code

// Problem: UVA12230 过河 Crossing Rivers
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/UVA12230
// Memory Limit: 0 MB
// Time Limit: 3000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include 

using namespace std;

const int N = 50007;

int n, m;
int d, kcase;
double p, l, v;

int main()
{
     
	while(scanf("%d%d", &n, &d) != EOF && n + d) {
     
		printf("Case %d: ", ++ kcase);
		double ans = 0;
		for(int i = 1; i <= n; ++ i) {
     
			scanf("%lf%lf%lf", &p, &l, &v);
			ans += 2.0 * l / v;
			d -= l;//减去河的宽度
		}
		printf("%.3f\n\n", ans + d);
	}
}

B. P4316 绿豆蛙的归宿（期望DP拓扑排序DP）

Problem

Solution

懒得写题解了…

Code

#include 

using namespace std;

const int N = 500007, M = 500007;

int t, n, m;
int head[N], ver[M], nex[M], edge[M], tot;
double dist[N];//从i到终点的期望距离
int out[N], deg[N];

void add(int x, int y, int z)
{
     
	ver[tot] = y;
	nex[tot] = head[x];
	edge[tot] = z;
	head[x] = tot ++ ;
}

void toposort()
{
     
	queue <int> q;
	q.push(n);
	while(q.size()) {
     
		int x = q.front();
		q.pop();
		for(int i = head[x]; ~i; i = nex[i]) {
     
			int y = ver[i];
			int z = edge[i];
			dist[y] += (dist[x] + (double)z) / deg[y];
			out[y] -- ;
			if(out[y] == 0) q.push(y);
		}
	}
}

int main()
{
     
	memset(head, -1, sizeof head);
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= m; ++ i) {
     
		int x, y, z;
		scanf("%d%d%d", &x, &y, &z);
		add(y, x, z);
		deg[x] ++ ;
		out[x] ++ ;
	}
	toposort();
	printf("%.2f\n", dist[1]);
	return 0;
}

C. P1850 [NOIP2016 提高组] 换教室（期望DP）

D. P3232 [HNOI2013]游走（期望DP + 列方程高斯消元）

https://www.luogu.com.cn/problem/P3232

E. AcWing 218. 扑克牌（简单期望DP）

Weblink

https://www.acwing.com/problem/content/220/

Problem

Solution

懒得写题解了

注意每次转移的时候需要翻开一张牌，所以期望次数 +1，所以我们转移的时候设 t = 1。

即：

$$\begin{array}{rlr}f[a][b][c][d][x][y]& =\frac{13-a}{Sum}f[a+1][b][c][d][x][y]& \\ & +\frac{13-b}{Sum}f[a][b+1][c][d][x][y]& \\ & +\frac{13-c}{Sum}f[a][b][c+1][d][x][y]& \\ & +\frac{13-d}{Sum}f[a][b][c][d+1][x][y]& \\ & +\underset{0\le i\le 3}{\min }f[a][b][c][d][i][y](x==4)& \\ & +\underset{0\le j\le 3}{\min }f[a][b][c][d][x][j](y==4)& \\ & +1& \end{array}$$

记忆化搜索即可。

Code

#include 

using namespace std;

const int N = 14, INF = 0x3f3f3f3f;

int n, m;
int A, B, C, D, x, y;
double f[N][N][N][N][5][5];

double dp(int a, int b, int c, int d, int x, int y)
{
     
	double &t = f[a][b][c][d][x][y];
	if(t >= 0) return t;
	
	int as = a + (x == 0) + (y == 0);
	int bs = b + (x == 1) + (y == 1);
	int cs = c + (x == 2) + (y == 2);	
	int ds = d + (x == 3) + (y == 3);

	if(as >= A && bs >= B && cs >= C && ds >= D) return t = 0;
	double sum = a + b + c + d + (x != 4) + (y != 4);
	sum = 54.0 - sum;
	if(sum <= 0) return INF;

	t = 1;//!
	
	if(a < 13) t += (13.0 - a) / (sum) * dp(a + 1, b, c, d, x, y);
	if(b < 13) t += (13.0 - b) / (sum) * dp(a, b + 1, c, d, x, y);
	if(c < 13) t += (13.0 - c) / (sum) * dp(a, b, c + 1, d, x, y);
	if(d < 13) t += (13.0 - d) / (sum) * dp(a, b, c, d + 1, x, y);
	
	if(x == 4) {
     
		double tmp = INF;
		for(int i = 0; i <= 3; ++ i) 
			tmp = min(tmp, dp(a, b, c, d, i, y) / sum);
		t += tmp;
	}
	
	if(y == 4) {
     
		double tmp = INF;
		for(int i = 0; i <= 3; ++ i) 
			tmp = min(tmp, dp(a, b, c, d, x, i) / sum);
		t += tmp;
	}
	return t;
}

int main()
{
     
	memset(f, -1, sizeof f);
	scanf("%d%d%d%d", &A, &B, &C, &D);
	double ans = dp(0, 0, 0, 0, 4, 4);
	if(ans > INF / 2) puts("-1.000");
	else printf("%.3f\n", ans);
	return 0;
}

F. P1291 [SHOI2002]百事世界杯之旅（收集问题）

Problem

双倍经验：（SP1026 FAVDICE - Favorite Dice）一个 $n$ 面的骰子，求期望掷几次能使得每一面都被掷到。

Input

17

Output

  340463
58------
  720720

Solution

我们设 $f[i]$ 表示已经买到 $i$ 个球星的期望购买次数。

考虑最后一次购买，若买到的是一个新球星，则：

$$f[i]+=(f[i-1]+1)\times \frac{n-(i-1)}{n}$$

若买到的是一个已经买过但不是第 $i$ 个买的球星，则：

$$f[i]+=(f[i]+1)\times \frac{i-1}{n}$$​

整理一下得：

$$f[i]=f[i-1]+\frac{n}{n-i+1}$$​

$$ans=\sum _{i=1}^n\frac{n}{n-i+1}=\sum _{i=1}^n\frac{n}{i}$$

显然最后的答案就是调和级数前缀和。

若数据较大的话可以 $O(1)$ 计算调和级数前缀和：

调和级数 $\sum _{i=1}^{\infty }\frac{1}{n}$ 的极限为 $lnn+C$，其中 $C=0.57721566490153286060651209$ 是欧拉常数

const int N = 500007;
double f[N];
int n;
int main()
{
     
    for(int i = 1; i <= N - 1; ++ i) 
        f[i] = f[i - 1] + 1.0 / i;
    while(scanf("%d", &n) != EOF) {
     
        if(n > N - 7) 
        	printf("%.4f\n", 0.57721566490153286060651209 + log(n + 1));
        else printf("%.4f\n", f[n]);
    }
    return 0;
}

Code

// Problem: P1291 [SHOI2002]百事世界杯之旅
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1291
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org) 

#include 
#define int long long
using namespace std;
//#define ll __int128;
typedef long long ll;
const int N = 107; 
int n, m;  
ll lcm(int a, int b)
{
     
	return a / __gcd(a, b) * b;
}

int get_len(int x)
{
      
	int len = 0;
	while(x) {
     
		x /= 10;
		len ++ ;
	}
	return len;
}

signed main()
{
     
	scanf("%lld", &n); 
	ll LCM = 1;
	for(int i = 1; i <= n; ++ i) {
      
		LCM = lcm(LCM, i);
	}	
	ll sum = 0;
	for(int i = 1; i <= n; ++ i) {
     
		sum += n * (LCM / i);
	}
	ll d = __gcd(sum, LCM);
	sum /= d, LCM /= d;
	if(LCM == 1) {
     
		cout << sum << endl;
		return 0;
	}
	ll mo = sum % LCM;
	ll l = sum / LCM;
	for(int i = 1; i <= get_len(l); ++ i) cout << " ";
	cout << mo << endl;
	cout << l;
	for(int i = 1; i <= get_len(LCM); ++ i) cout << "-";
	puts("");
	for(int i = 1; i <= get_len(l); ++ i) cout << " ";
	cout << LCM << endl;
	return 0;
}

G. P1654 OSU!（立方的期望）

Problem

Solution

设 $a_i$ 表示前 $i$ 位中第 $i$ 位为 $1$ 的长度的期望，$b_i$ 表示前 $i$ 位中第 $i$ 位为 $1$ 的长度的平方的期望，$c_i$ 表示前 $i$ 位中第 $i$ 位为 $1$ 的长度的立方的期望。

则有：

$$a[i]=(a[i-1]+1)\times p[i]$$

即第 $i$ 位以 $p[i]$ 的概率为 $1$，由第 $i-1$ 位同样为 $1$ 的长度的期望 $+1$ 而来。

$$b[i]=(b[i-1]+2\times a[i-1]+1)\times p[i]$$

即： $(x+1{)}^2=x^2+2x+1$

同理有：

$$c[i]=(c[i-1]+3\times b[i-1]+3\times a[i-1]+1)\times p[i]$$

即 $a,b,c$ 的前提都是一样的 ：连续的 $1$。

最后答案是期望长度的立方 ，而这里 $c[i]$ 是指第 $i$ 位为 $1$ 的长度的期望，还有第 $i$ 位为 $0$ 的情况，故：

$$\begin{array}{rlr}c[i]& =(c[i-1]+3\times b[i-1]+3\times a[i-1]+1)\times p[i]+c[i-1]\times (1-p[i])& \\ & =c[i-1]+(3\times b[i-1]+3\times a[i-1]+1)\times p[i]& \end{array}$$

Code

// Problem: P1291 [SHOI2002]百事世界杯之旅
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P1291
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org) 

#include 
using namespace std;

const int N = 500007;

int n, m;
double a[N], b[N], c[N], p[N];
double ans;

int main()
{
     
	scanf("%d", &n);
	for(int i = 1; i <= n; ++ i) {
     
		scanf("%lf", &p[i]);
		a[i] = (a[i - 1] + 1) * p[i];
		b[i] = (b[i - 1] + 2 * a[i - 1] + 1) * p[i];
		c[i] = c[i - 1] + (3 * b[i - 1] + 3 * a[i - 1] + 1) * p[i];
	}
	 
	printf("%.1f\n", c[n]);
	return 0;
}

三倍经验：
https://www.luogu.com.cn/problem/P1365
https://www.luogu.com.cn/problem/CF235B

H. P3802 小魔女帕琪（期望 + 组合数学）

Problem

Solution

Code

// Problem: P3802 小魔女帕琪
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3802
// Memory Limit: 125 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org) 
#include  
using namespace std; 
const int N = 50007; 
double a[N];
int n;

int main()
{
     
	double fact7 = 1; 
	double sum = 0;
	double ans;
	for(int i = 1; i <= 7; ++ i)
		scanf("%lf", &a[i]), sum += a[i], fact7 *= i;
	ans = fact7 * a[1] / sum * a[2] / (sum - 1) * a[3] / (sum - 2) * a[4] / (sum - 3) * a[5] / (sum - 4) * a[6] / (sum - 5) * a[7];
	printf("%.3f\n", ans);
	return 0;
}

I. 牛客挑战赛36 D. 排名估算（ “概率论全家桶”，好题，拉格朗日插值求自然数 k 次幂之和）

Weblink

https://ac.nowcoder.com/acm/contest/3782/D

Problem

期末考后，小 C 登录了学校的成绩查询系统，却发现自己的排名被屏蔽了。为了知道自己的排名，小 C 使用了系统中的“好友伴学”功能。每次，系统会在除了小 C 之外的所有考生中随机抽取一名，然后返回 Ta 的排名比小 C 高还是低。这次考试有 $n$ 个人参加，小 C 总共使用的 $m$ 次 “好友伴学” 功能，却没有一次抽中排名比自己高的人。请问小C在这次考试中的期望排名是多少?

$2\le n\le 10^{11},0\le m\le 5000$

假设小C的的期望排名化为最简分数后是 $p/q$，输出 $p\ast q^{-1}\mathrm{m}\mathrm{o}\mathrm{d}998244353$。

Solution

设 $p_i$ 表示排名为第 $n-i$ 时，$m$ 次没抽中排名比自己高的人（排名高指排名在自己前面hhh）的概率。

显然排名只有 $1\sim n$，则对于 $0\le i\le n-1$，$p_i=(\frac{i}{n-1}{)}^m$（排名 $n-i$，则比自己排名高的一共有 $n-i$ 个人，没有抽中显然是抽到了自己后面的 $i$ 排名低的人）

令事件 $A$ 为 $m$ 次没抽中，事件 $B_i$ 为排名为 $n-i$ 。

根据乘法公式：$P(A{B}_i)=P(A|B_i)\times P(B_i)=P(B_i|A)\times P(A)$，

我们首先计算 $P(A)$，根据全概率公式：

$$P(A)=\sum _{i=0}^{n-1}P(B_i)\times P(A|B_i)$$

即排名为 $i$ 的前提下事件$A$ ，$m$ 次没抽中的概率之和。

显然

$$P(B_i)=\frac{1}{n}，P(A|B_i)=p_i=(\frac{i}{n-1}{)}^m$$

则

$$P(A)=\sum _{i=0}^{n-1}(\frac{i}{n-1}{)}^m\times \frac{1}{n}$$

代入贝叶斯公式：

$$\begin{array}{rlr}P(B_i|A)& =\frac{P(B_i)\times P(A|B_i)}{\sum _{j=0}^{n-1}P(B_j)\times P(A|B_j)}& \\ & =\frac{p_i\times \frac{1}{n}}{\sum _{j=0}^{n-1}{p}_j\times \frac{1}{n}}& \end{array}$$

期望 $E(x)=P\times x$

$x$ 是排名，$p$ 为排名为 $x$ 时抽 $m$ 次抽不到的概率。

显然答案为：
$$\begin{array}{rlr}ans& =\sum _{x=1}^{n}E(x)& \\ & =\sum _{x=1}^{n}P(B_i|A)\times (n-i)& \\ & =\sum _{i=0}^{n-1}\frac{p_i\times \frac{1}{n}\times (n-i)}{\sum _{j=0}^{n-1}{p}_j\times \frac{1}{n}}& \\ & =\frac{\sum _{i=0}^{n-1}{p}_i\times (n-i)}{\sum _{i=0}^{n-1}{p}_i}& \\ & =n-\frac{\sum _{i=0}^{n-1}{i}^{m+1}}{\sum _{i=0}^{n-1}{i}^m}& \end{array}$$

显然答案就是一个自然数 $k$ 次幂之和，我们使用拉格朗日插值 $O(n)$ 计算即可。

特判一下 $m=0$ 的情况，即不抽，那么期望就是：

$$E(x)=P\times x=\frac{1}{n}\times \sum _{i=1}^{n}i=\frac{1}{n}\times \frac{n(n+1)}{2}=\frac{n+1}{2}$$

当然不需要化简为最简分数，因为除法转换成逆元乘起来是等价的。

Code

// Problem: 排名估算
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/3782/D
// Memory Limit: 524288 MB
// Time Limit: 2000 ms
// 
// Powered by CP Editor (https://cpeditor.org)


#include 
#define int long long
using namespace std;

const int N = 5007, M = 5007, mod = 998244353;
 
int read(){
     
    int s = 0, ne = 1; char c = getchar();
    while(c < '0' || c > '9') {
     if(c == '-') ne = -1; c = getchar();}
    while(c >= '0' && c <= '9') s = (s << 1) + (s << 3) + c - '0', c = getchar();
    return s * ne;
}

int qpow(int a, int b)
{
     
	int res = 1;
	while(b) {
     
		if(b & 1) res = 1ll * res * a % mod;
		a = 1ll * a * a % mod; 
		b >>= 1;
	} 
	return res;
}
 
int s[N], pre[N], suf[N], infact[N], fact[N];

void init(int k)
{
      
	infact[0] = fact[0] = 1;
	for(int i = 1; i <= k + 10; ++ i)
		fact[i] = 1ll * fact[i - 1] * i % mod;
	infact[k + 10] = qpow(fact[k + 10], mod - 2);
	for(int i = k + 9; i >= 0; -- i)  
		infact[i] = 1ll * infact[i + 1] * (i + 1) % mod;
	infact[0] = 1; 
}
 
int lagrange(int n, int k)
{
      
	int ans = 0; 
	s[0] = 0;
 	for(int i = 1; i <= k + 2; ++ i)
 		s[i] = (s[i - 1] + qpow(i, k)) % mod;
	
	if(n <= k + 1)  
		return s[n];  
	
	pre[0] = 1;
	for(int i = 1; i <= k + 2; ++ i)
		pre[i] = 1ll * pre[i - 1] * ((n - i + mod) % mod) % mod;
	suf[k + 3] = 1;
	for(int i = k + 2; i; -- i)
		suf[i] = 1ll * suf[i + 1] * ((n - i + mod) % mod) % mod;
		
	for(int i = 0; i <= k + 2; ++ i) {
     
		s[i] = 1ll * s[i] * pre[i - 1] % mod * suf[i + 1] % mod * infact[i - 1] % mod * infact[k + 2 - i] % mod;
		if((k + 2 - i) & 1) 
			ans = (1ll * ans - s[i] + mod) % mod;
		else ans = (1ll * ans + s[i]) % mod;
	}
	return (ans + mod) % mod;
}
 
int n, m;
 
signed main()
{
     
	init(M - 5);
	scanf("%lld%lld", &n, &m);
	if(m == 0) {
     
		printf("%lld\n", (n + 1) % mod * qpow(2, mod - 2) % mod);
		return 0;
	}
	int up = lagrange(n - 1, m + 1); 
	int down = lagrange(n - 1, m); 
	down = qpow(down, mod - 2);
	printf("%lld\n", (n - up * down % mod + mod) % mod);
}

J. 牛客挑战赛38 C.圆桌聚餐（条件概率，贝叶斯公式，期望 dp，思维）

https://blog.csdn.net/qq_41997978/article/details/105053785?utm_medium=distribute.pc_relevant.none-task-blog-baidujs_title-1&spm=1001.2101.3001.4242

Problem

Solution

Code

K. ABC 199 F - Graph Smoothing（数学期望，图的邻接矩阵幂的意义，矩阵快速幂）

Weblink

https://atcoder.jp/contests/abc199/tasks/abc199_f

Problem

Solution

我们要知道图的邻接矩阵的幂的意义，详见 P3758 [TJOI2017]可乐

解题报告（九） 矩阵与行列式（ACM / OI）超高质量题解

这个图就非常形象：

读题之后发现显然就是建图然后求 $k$ 次幂即可，因为有 $k$ 次互不影响的操作嘛。

我们拥有的操作是等概率地选择一条边，将这条边连接的两个点的点权变成两个点的点权的平均值。显然很难维护每一条边连接的两个点的平均值，所以我们换个思想，仅需维护每一个点得到的贡献即可。

显然对于每一个点的期望权值，只有自己对自己的贡献（概率），以及自己所连向的点对自己的贡献。

我们设 $d_i$ 为点 $i$ 的度数。

首先考虑自己对自己的贡献：

那么对于一个点来说，不做任何操作的话对自己的贡献即为自己的点权 $a_i$，但是当我选择一条边的时候，每一个点一共连有 $d_i$ 条边，所以每一个点被选中的概率显然为 $\frac{d_i}{m}$，那么一个点被选中之后，它自己的贡献就从 $a_i$ 变成了 $\frac{a_i}{2}$（因为我们进行的是取平均数的操作），所以原来的期望为 $1\times a_i$ ，每次有 $\frac{d_i}{m}$ 的概率选到点 $i$，被选择一次期望权值就减少 $\frac{a_i}{2}$，即 贡献为 $1-\frac{d_i}{2\times m}=\frac{2\times m-d_i}{2\times m}$。自己（$i$）对自己（$i$）的贡献就是邻接矩阵里的 $a[i][i]$。

然后考虑其他与之相连的点对自己的贡献：

那么对于任意一条边 $⟨u,v⟩$，考虑点 $u$ 对点 $v$ 的贡献，显然选择到该边的概率为 $\frac{1}{m}$， $u$ 给 $v$ 的贡献就是平均数 $\frac{1}{2}$。别人（$j$）给自己（$i$）的贡献就是邻接矩阵里的 $a[j][i]$。

我们计算出每一个点得到的贡献（概率）之后，自己对自己的贡献乘上自己本身的点权，别人对自己的贡献（概率）乘上别人的点权就是每个点在 $k$ 次操作后的点权的期望。

Time

$O(n^{3}logk)$
Code

// Problem: F - Graph Smoothing
// Contest: AtCoder - AtCoder Beginner Contest 199（Sponsored by Panasonic）
// URL: https://atcoder.jp/contests/abc199/tasks/abc199_f
// Memory Limit: 1024 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)

#include 

using namespace std;
#define int long long
typedef long long ll;
const int N = 507, mod = 1e9 + 7;

int res[N][N];
int a[N][N];
int val[N];
int e[N][N];
int n, m, k;
int d[N];

void mul(int c[], int a[], int b[][N])
{
     
	int tmp[N] = {
     0};
	for(int j = 1; j <= n; ++ j)
		for(int k = 1; k <= n; ++ k)
			tmp[j] = (tmp[j] + a[k] * b[k][j]) % mod;
	memcpy(c, tmp, sizeof tmp);
}

void mul(int c[][N], int a[][N], int b[][N])
{
     
	int tmp[N][N] = {
     0};
	for(int i = 1; i <= n; ++ i)
		for(int j = 1; j <= n; ++ j)
			for(int k = 1; k <= n; ++ k)
				tmp[i][j] = (tmp[i][j] + a[i][k] * b[k][j]) % mod;
	memcpy(c, tmp, sizeof tmp);
} 

int qpow(int a, int b)
{
     
	int res = 1;
	while(b) {
     
		if(b & 1) res = 1ll * res * a % mod;
		a = 1ll * a * a % mod;
		b >>= 1;
	}
	return res;
}

signed main()
{
     
	scanf("%lld%lld%lld", &n, &m, &k);
	for(int i = 1; i <= n; ++ i)
		scanf("%lld", &val[i]);
	for(int i = 1; i <= m; ++ i) {
     
		int x, y;
		scanf("%lld%lld", &x, &y);
		e[x][y] = e[y][x] = 1;
		d[x] ++ ;
		d[y] ++ ;
	}
	int inv_2m = qpow(2 * m, mod - 2);

	for(int i = 1; i <= n; ++ i) {
     
		for(int j = 1; j <= n; ++ j) {
     
			if(e[i][j]) {
     
				a[j][i] = inv_2m;//别人给自己的贡献（j 给 i 的贡献）
			}
		}//自己给自己的贡献（i 给 i 的贡献）
		a[i][i] = (2 * m - d[i]) * inv_2m % mod;
	}

	for(int i = 1; i <= n; ++ i)
		res[i][i] = 1; 

	while(k) {
     
		if(k & 1) mul(res, res, a);
		mul(a, a, a);
		k >>= 1;
	} 

	for(int i = 1; i <= n; ++ i) {
     
		ll ans = 0;
		for(int j = 1; j <= n; ++ j) 
			ans = (ans + (1ll * res[j][i] * val[j]) % mod) % mod; 
		cout << ans << endl;
	}
	return 0;
}

L. 牛客挑战赛 38 D.突击检查（期望 + 思维）

Problem

Solution

Code
https://blog.csdn.net/qq_41997978/article/details/105043239?utm_medium=distribute.pc_relevant_t0.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-1.control&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Edefault-1.control

M. P4550 收集邮票（期望DP）

Weblink

https://www.luogu.com.cn/problem/P4550

Problem

有 $n$ 种不同的邮票，皮皮想收集所有种类的邮票。唯一的收集方法是到同学凡凡那里购买，每次只能买一张，并且买到的邮票究竟是 $n$ 种邮票中的哪一种是等概率的，概率均为 $\frac{1}{n}$ 。但是由于凡凡也很喜欢邮票，所以皮皮购买第 $k$ 次邮票需要支付 $k$ 元钱。

现在皮皮手中没有邮票，皮皮想知道自己得到所有种类的邮票需要花费的钱数目的期望。

Solution

Code

N. UVA1639 Candy（防爆对指数 + 二项分布 + 期望）

Weblink

https://www.luogu.com.cn/problem/UVA1639

Problem

有两个盒子各有n (n<=2e5) 个糖，每天随机选一个（概率分别为p，1-p），然后吃一颗糖。直到有一天，打开盒子一看，没糖了！输入n，p，求此时另一个盒子里糖的个数的数学期望。

Solution

显然是二项分布，当我们发现一个盒子没糖的时候，也就意味着我们是第 $n+1$ 次打开这个糖果盒子，假设设个盒子是第一个盒子，即选择一次它的概率为 $p$ ，那么另一个糖果盒的概率为 $1-p$ 显然第二个盒子打开的次数不一定，可以是 $i=0,1,2,3,4,5\cdots n$，即概率为：$P_a=C_{2n-i}^n{p}^{n+1}(1-p{)}^{n-i}$

若没有糖果的盒子是第二个盒子，则概率为：$P_b=C_{2n-i}^n(1-p{)}^{n+1}(p{)}^{n-i}$

则期望为 $EX={\sum }_{i=0}^n(i\times (P_a+P_b))$

但是 $n\le 2\times 10^5$，直接计算组合数的话没有给模数是一定会炸的，所以我们可以使用对指技巧，计算它的对数，然后求它的指数即可。

即：
$$\begin{array}{ccc}& \ln P_a=\ln \left(C_{2n-i}^n\ast p^{n+1}\ast (1-p{)}^{n-i}\right)& \\ & \ln P_b=\ln C_{2n-i}^n+\ln p^{n+1}+\ln (1-p{)}^{n-i}& \\ & \ln P_a=\ln (2n-i)!-\ln n!-\ln (n-i)!+(n+1)\ln p+(n-i)\ln (1-p)& \\ & \ln P_b=\ln (2n-i)!-\ln n!-\ln (n-i)!+(n+1)\ln (1-p)+(n-i)\ln p& \\ & EX={\sum }_{i=1}^n\left(i\ast \left(e^{\ln P_a}+e^{\ln P_b}\right)\right)& \end{array}$$
我们可以先预处理一下 $n!$ 的对数，注意这里要用 long double 来存，否则会炸精度。

Code

// Problem: UVA1639 糖果 Candy
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/UVA1639
// Memory Limit: 0 MB
// Time Limit: 3000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include 

using namespace std;
using ld = long double;
const int N = 2e5 + 7;

int n, m;
ld p;
int t;
ld f[N << 1];

void init(int n)
{
      
	for(int i = 1; i <= 400000; ++ i) {
     
		f[i] = f[i - 1] + (ld)log(i);
	}
}

int kcase;

int main()
{
     
	init(N - 7);
	while(scanf("%d%Lf", &n, &p) != EOF) {
     
		printf("Case %d: ", ++ kcase);
		ld EX = 0.0;
		ld P = log(p);
		ld Q = log(1 - p);
		for(int i = 0; i <= n; ++ i) {
     
			ld w1 = f[2 * n - i] - f[n] - f[n - i] + (n + 1) * Q + (n - i) * P;
			ld w2 = f[2 * n - i] - f[n] - f[n - i] + (n + 1) * P + (n - i) * Q;
			EX += i * (exp(w1) + exp(w2));
		}
		printf("%.6Lf\n", EX);
	}
	return 0;
}

O. P4206 [NOI2005] 聪聪与可可 （记忆化搜索期望DP + SPFA预处理）

Weblink

https://www.luogu.com.cn/problem/P4206

Problem

在一个魔法森林里，住着一只聪明的小猫聪聪和一只可爱的小老鼠可可。

整个森林可以认为是一个无向图，图中有 $N$ 个美丽的景点，景点从 $1$ 至 $N$
编号。在景点之间有一些路连接。
可可正在景点 $M(M\le N)$ 处。以后的每个时间单位，可可都会选择去相邻
的景点（可能有多个）中的一个或停留在原景点不动。而去这些地方所发生的概
率是相等的。
聪聪是很聪明的，所以，当她在景点 C 时，她会选一个更靠近可可的景点，
如果这样的景点有多个，她会选一个标号最小的景点。如果走完第一步以后仍然
没吃到可可，她还可以在本段时间内再向可可走近一步。
在每个时间单位，假设聪聪先走，可可后走。在某一时刻，若聪聪和可可位
于同一个景点，则可可就被吃掉了。
问平均情况下，聪聪几步就可能吃到可可。

Solution

根据题目要求聪聪会向可可不断靠近，且边无权，所以先设边权为 $1$ ，对于每一个点进行一次 SPFA ，预处理出 $p[i,j]$ ，表示顶点 $i$ 到顶点 $j$ 的最短路上与顶点 $i$ 相邻且编号最小的顶点编号。即聪聪在景点 $i$，可可在景点 $j$ 时，聪聪第 $1$ 步会走到的景点编号。

设 $f[i,j]$ 来表示聪聪在顶点 $i$，可可在顶点 $j$ 时聪聪抓住可可的平均步数，即期望步数。令 $w[i,j]$ 表示与顶点 $i$ 相邻的 $j$ 个点编号，而用 $d[i]$ 表示顶点 $i$ 的度数。

显然聪聪下一步所在的顶点即为 $p[p[i,j],j]$，可可下一步在顶点 $w[i,j]$ 的概率为 $\frac{1}{d[i]+1}$，下一步这个情况下的期望 $f[p[p[i,j],j],w[i,j]]$ 已经计算出，那么就是比 $f[p[p[i,j],j],w[i,j]]$ 多出一步。可可在原地停留的情况则类似。

有转移方程：

$$\begin{array}{rlr}f[i,j]& =\frac{(\sum _{k=1}^{t[i]}f[p[p[i,j],j],w[j,k]]+1)+f[p[p[i,j],j],j]+1}{d[i]+1}+1& \\ & =\frac{(\sum _{k=1}^{t[i]}f[p[p[i,j],j],w[j,k]])+f[p[p[i,j],j],j]+d[i]+1}{d[i]+1}& \\ & =\frac{(\sum _{k=1}^{t[i]}f[p[p[i,j],j],w[j,k]])+f[p[p[i,j],j],j]}{d[i]+1}+1& \end{array}$$

• 若 $i==j$，则 $f[i,i]=0$ 。

• 若 $p[p[i,j],j]=j$ 或 $p[i,j]=j$ 则说明在这一步聪聪即可吃掉可可，那么 $f[i,j]=1$。

记忆化搜索即可。

Code

// Problem: P4206 [NOI2005] 聪聪与可可
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4206
// Memory Limit: 125 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)

#include 

using namespace std;

const int N = 1e3 + 7, M = 2e3 + 7, INF = 0x3f3f3f3f;

int n, m, s, t;
int head[N], edge[M], ver[M], nex[M], tot;
bool vis[N];
int p[N][N];
int dist[N][N];
double f[N][N];
int d[N];

void add(int x, int y, int z)
{
     
	ver[tot] = y;
	edge[tot] = z;
	nex[tot] = head[x];
	head[x] = tot ++ ;
	d[x] ++ ; 
}

void SPFA(int s)
{
     
	memset(dist, -1, sizeof dist); 
	vis[s] = 1;
	dist[s][s] = 0;
	queue<int> q;
	q.push(s);
	while(q.size()) {
     
		int x = q.front();
		q.pop();
		vis[x] = 0;
		for(int i = head[x]; ~i; i = nex[i]) {
     
			int y = ver[i];
			int z = edge[i];
			if(dist[s][y] == -1 || (dist[s][y] == dist[s][x] + z && p[s][x] < p[s][y])) {
     
				dist[s][y] = dist[s][x] + z;
				if(p[s][x]) {
     
					p[s][y] = p[s][x];
				}
				else p[s][y] = y;
				if(vis[y] == 0) {
     
					vis[y] = 1;
					q.push(y);
				}
			}
		}
	}
}

//记忆化搜索
double dfs(int x, int y)
{
     
	if(f[x][y]) {
     
		return f[x][y];
	}
	if(x == y){
     
		return f[x][y] = 0.0;
	}
	if(p[x][y] == y || p[p[x][y]][y] == y) {
     
		return f[x][y] = 1.0;
	}
	for(int i = head[y]; ~i; i = nex[i]) {
     
		int nex_node = ver[i];
		f[x][y] += dfs(p[p[x][y]][y], nex_node);
	}
	f[x][y] = (f[x][y] + dfs(p[p[x][y]][y], y)) / (d[y] + 1) + 1;
	return f[x][y];
}

double ans;

int main()
{
     
	memset(head, -1, sizeof head);
	scanf("%d%d", &n, &m);
	scanf("%d%d", &s, &t);
	for(int i = 1; i <= m; ++ i) {
     
		int x, y;
		scanf("%d%d", &x, &y);
		add(x, y, 1);
		add(y, x, 1);
	}
	for(int i = 1; i <= n; ++ i)
		SPFA(i);
	ans = dfs(s, t);
	printf("%.3f\n", ans);
	return 0;
}

P. P4745 [CERC2017]Gambling Guide（期望DP + 最短路）

Weblink

https://www.luogu.com.cn/problem/P4745

Problem

Solution

显然考虑期望 $dp$ 。因为只有一个终点 $n$，且状态已知，考虑逆推。

设 $f[x]$ 表示点 $x$ 到 $n$ 的期望花费，或者可以说是从 $n$ 到点 $x$ 的期望花费。 $d[x]$ 表示 $x$ 点的度数，则有

$$f[x]=\frac{\sum \min \{f[x],f[y]\}}{d[x]}+1$$

即，花费一枚硬币，选择原地不动，或者从 $y$ 走到 $x$ ，到达点 $x$ 一共有 $d[x]$ 条路，即一共有 $d[x]$ 种情况，所以概率期望就是$\frac{1}{d[x]}$，花费的期望就为 总花费乘上 $\frac{1}{d[x]}$。

观察公式显然可以发现对于一个点 $x$ ，所有与 $x$ 相邻的点 $y$，能对 $x$ 产生贡献，当且仅当 $f[y]<f[x]$ 。

假设对于点 $x$ 而言，满足上述条件（$f[y]<f[x]$）的相邻点 $y$ 点一共有 $cnt[x]$ 个，则有

$$\begin{array}{rlr}f[x]& =\frac{(d[x]-cnt[x])\times f[x]+\sum f[y]+cnt[x]}{d[x]}& \\ & =\frac{\sum f[y]+d[x]}{cnt[x]}& \end{array}$$

显然 $\sum f[y]$ 可以直接把所有小于 $f[x]$ 的都加起来，可以用最短路去实现，因为我们每次从队里拿出来的一定是最小的 $f[y]$，那么所有与他相邻的点都可以被他更新，我们就可以对于每一个 $x$ 能到达的点 $y$ ，求和，即 $sum[y]=\sum f[x]$。然后对于每一个点 $y$ ，直接根据公式更新 $f[y]$ 即可。

更新的时候，是从 $n$ 出发，走到 $1$ ，即每次从 $x$ 走到 $y$ ，那么公式中的 $x$ 就是 $y$ ，也就是用所有 的 $x$ 去更新 $y$，每次更新的是 $f[y]$ 而不是公式里的 $f[x]$。

Code

int n, m, t;
int head[N], ver[M], edge[M], tot, nex[N];
double d[N], cnt[N], sum[N];
double dist[N];
bool vis[N];

void add(itn x, int y)
{
     
    ver[tot] = y;
    nex[tot] = head[x];
    head[x] = tot ++ ;
}

void dijkstra()
{
     
    memset(dist, 0x3f, sizeof dist);
    dist[n] = 0;
    priority_queue<PDI, vector<PDI>, greater<PDI> > q;
    q.push({
     0.0, n});
    while(q.size()) {
     
        itn x = q.top().second;
        q.pop();
        if(vis[x]) continue;
        vis[x] = 1;
        for(int i = head[x]; ~i; i = nex[i]) {
     
            itn y = ver[i];
            if(vis[y]) continue;
            cnt[y] ++ ;
            sum[y] += dist[x];
            dist[y] = (d[y] + sum[y]) / cnt[y];
            q.push({
     dist[y], y});
        }
    }
}

int main()
{
     
    memset(head, -1, sizeof head);
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= m; ++ i) {
     
        itn x, y;
        scanf("%d%d", &x, &y);
        add(x, y);
        add(y, x);
        d[x] ++ ;
        d[y] ++ ;
    }
    dijkstra();

    printf("%.8f\n", dist[1]);
    return 0;
}

Q. UVA12177 First Knight（期望DP + 高斯消元 + 优化）

Problem
Solution


$f(x,y)$ 对其他方程进行消元时，最多也只会影响到 $f(x,y+1),f(x-1,1),f(x-1,y)$ 这几项的系数，所以我们只需要讲矩阵消成下三角矩阵，并且我们只需要 $a[1][1]$ 的值，可以去掉回带的操作，跑了 $1.5s$

Code

// Problem: UVA12177 First Knight
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/UVA12177
// Memory Limit: 0 MB
// Time Limit: 9000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

#include 

using namespace std;

const int N = 57;
const double eps = 1e-12;

int dir[4][2] = {
     1, 0, 0, 1, -1, 0, 0, -1};
double p[N][N][4];
int n, m, t;
int r;

int get_id(int x, int y)
{
     
	if(x < 1 || y < 1 || x > n || y > m) return r + 5;
	return (x - 1) * m + y;
}

struct Matrix 
{
     
	int equ, var;//equ -> 等式个数  var -> 未知变量个数
	double a[N * N][N * N];
	void clear() {
     
		for (int i = 1; i <= equ; ++ i) 
			for (int j = 1; j <= var + 1; ++ j) 
				a[i][j] = 0;
	}
	
	double guass() {
     
		for (int i = equ - 1, col = var - 1; i >= 1 && col >= 1; -- i, -- col) {
     
			for (int j = i - 1; j >= 1; -- j) {
     
				double tmp = a[j][col] / a[i][col];
				if(fabs(tmp) < eps) continue;
				for (int k = col; k >= 1; -- k) 
					a[j][k] -= a[i][k] * tmp;
				a[j][var + 1] -= a[i][var + 1] * tmp;
			}
		}   
		return a[1][var + 1] / a[1][1];
	} 
}M;

int main()
{
     
	
	while (scanf("%d%d", &n, &m) != EOF && n + m) {
     
		for (int k = 0; k < 4; ++ k) {
     
			for (int i = 1; i <= n; ++ i) {
     
				for (int j = 1; j <= m; ++ j) {
     
					scanf("%lf", &p[i][j][k]);
				}
			}
		} 
		r = n * m;
		M.equ = M.var = n * m;
		M.clear();
		for (int i = 1; i <= n; ++ i) {
     
			for (int j = 1; j <= m; ++ j) {
     
				int id = get_id(i, j);
				M.a[id][id] = -1;
				if (i == n && j == m) continue;
				M.a[id][r + 1] = -1;
				for (int k = 0; k < 4; ++ k) {
     
					int now_id = get_id(i + dir[k][0], j + dir[k][1]);
					M.a[id][now_id] = p[i][j][k];
				} 
			}
		}  
		puts("");*/
		printf("%.1f\n", M.guass());
	}
	return 0;
}

R. CF24D Broken robot（期望DP + 高斯消元）

Weblink

Problem

Solution

Code

S. UVA 10900 So you want to be a 2n-aire?（连续型概率，均匀分布）

Weblink

https://vjudge.net/problem/UVA-10900

Problem

一个娱乐节目中，刚开始玩家初始的金额为1，有n道题目，答对每一道题目的概率在t到1之间均匀分布，每答一道题，答对的话奖金翻倍，答错的话结束游戏，一分也拿不到。每次听到问题后可以选择答题与不答题，不答题则游戏结束。求玩家在最优策略下能获得的奖金的期望值。

Solution

草稿纸凑合看吧（）

Code

T. CF1139D Steps to One（期望，莫比乌斯反演，杜教筛）

Weblink

2021年天梯赛 L3-3 可怜的简单题

CF1139D

Problem

Solution

数据较大，要用快速乘不然会爆 long long

Code

#include 
using namespace std; 
#define ll long long
const int N = 21544400 + 7;

#define minus(x, y) (1ll * x - y < 0 ? 1ll * x - y + mod : 1ll * x - y)
#define plus(x, y) (1ll * x + y >= mod ? 1ll * x + y - mod : 1ll * x + y) 

ll mod;
int mu[N];
ll smu[N];
bool vis[N];
unordered_map <ll, ll> sum_mu;
int primes[N], cnt;
ll n, m; 

ll mul(ll a, ll b) {
     
    if (mod <= 1000000000) return a * b % mod;
    else if (mod <= 1000000000000ll) return (((a * (b >> 20) % mod) << 20) + (a * (b & ((1 << 20) - 1)))) % mod;
    else {
     
        ll d = (ll)floor(a * (long double)b / mod + 0.5);
        ll res = (a * b - d * mod) % mod;
        if (res < 0) res += mod;
        return res;
    }
}

ll qpow(ll a, ll b)
{
     
	if(mod == 1) return 0;
	ll res = 1;
	a = a % mod;
	while(b) {
     
		if(b & 1) res = mul(res, a);
		a = mul(a, a);
		b >>= 1;
	}
	return res;
}

ll inv(ll x)
{
     
	return qpow(x, mod - 2);
}

void init(int n)
{
     
	mu[1] = 1, vis[1] = 1;
	for(int i = 2; i <= n; ++ i) {
     
		if(vis[i] == 0) {
     
			primes[ ++ cnt] = i;
			mu[i] = -1;
		}
		for(int j = 1; j <= cnt && i * primes[j] <= n; ++ j) {
     
			vis[i * primes[j]] = 1;
			if(i % primes[j] == 0) {
     
				mu[i * primes[j]] = 0;
				break;
			}	
			mu[i * primes[j]] -= mu[i];
		}
	}	
	for(int i = 1; i <= n; ++ i) 
		smu[i] = plus(smu[i - 1], mu[i]);
	return ;
}

inline ll g_sum(ll x)
{
     
	return x;
}

inline ll get_sum_mu(ll x)
{
     
	if(x <= N - 7) return smu[x];
	if(sum_mu.find(x) != sum_mu.end()) return sum_mu[x]; 

	ll ans = 1;
	for(ll l = 2, r; l <= x; l = r + 1) {
     
		r = x / (x / l); 
		ll tmp = mul((r - l + 1), get_sum_mu(x / l));
		ans = minus(ans, tmp);
	}
	ans = (ans % mod + mod) % mod;
	sum_mu[x] = ans / g_sum(1ll);
	return ans / g_sum(1ll); 
}

void solve(ll m)
{
     
	ll ans = 1;
	for(ll l = 1, r; l <= m; l = r + 1) {
     
		r = m / (m / l); 
		ll tmp = mul((get_sum_mu(r) - get_sum_mu(l - 1)), mul(m / l, inv(m - m / l)));
		ans = minus(ans, tmp);
	}  
	ans = (ans + mod) % mod;
	printf("%lld\n", ans);
	return ;
}

signed main()
{
      
	scanf("%lld%lld", &m, &mod);
	if(m == 1) return printf("1\n"), 0;
	init(N - 7);
	solve(m);
	return 0;
}

U. LightOJ 1274 Beating the Dataset（期望，贡献和思想）

Weblink

https://vjudge.net/problem/LightOJ-1274

Problem

给定0和1的个数，这些0、1产生的任何一个多重集排列都是可能的，求所有可能的n位01排列中第一位为0的位或者与排列中前面一位不同的位的期望个数。

Solution

草稿纸凑合看吧（）

Code

#include  
using namespace std; 
const int N = 5e5 + 7;

int t, kcase;
int n, m, x, y, s;

int main()
{
     
	scanf("%d", &t);
	while(t -- ) {
     
		scanf("%d%d", &n, &s);
		x = s - 2 * n;
		y = 3 * n - s;
		printf("Case %d: %.10f\n", ++ kcase, (2.0 * x * y + y) / n);
	}
}

V. 牛客练习赛82 D. Mocha 的数据包

Weblink

https://ac.nowcoder.com/acm/contest/11172/D

Problem

Solution

大概是这么个意思吧

Code

W. HDU 4579 Random Walk（期望 + 高斯消元）

X. HDU 6829 Borrow

Y. HDU 6052 To my boyfriend（贡献和）

Z. HDU 4870 Rating

α. LightOJ 1151 Snakes and Ladders

β. P4457 [BJOI2018]治疗之雨（期望 + 高斯消元）

γ. P3600 随机数生成器

%**Weblink****Problem****Solution****Code**

%https://blog.csdn.net/consciousman/article/details/73730834?utm_source=app&app_version=4.5.8

%https://www.luogu.com.cn/blog/ShineEternal/mathematical-expectation

%https://blog.csdn.net/hollyidyllic/article/details/108060378?utm_medium=distribute.pc_relevant.none-task-blog-baidujs_title-0&spm=1001.2101.3001.4242

%R. LightOJ 1274 Beating the Dataset

%Q. LightOJ 1265 Island of Survival

%S. LightOJ 1284 Lights inside 3D Grid

%LightOJ – 1342 Aladdin and the Magical Sticks

%https://blog.csdn.net/u011699990/article/details/38115811?utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromMachineLearnPai2%7Edefault-1.control&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromMachineLearnPai2%7Edefault-1.control