时间序列数据分析--Time Series--时序模型--ARIMA-股票分析
使用ARIMA模型拟合股票数据
ARIMA可拆分为AR , I , MA。
AR模型:
MA模型:
ARMA模型:
ARIMA模型:
ARIMA:差分自回归移动平均模型
- AR是自回归,P是自回归项;
- d 为时间序列称为平稳时 所做的差分次数
- MA 是移动平均, q 为移动平均项
- 原理: 将非平稳时间序列转换成平稳时间序列, 然后将因变量仅对它的滞后值(p阶)以及随机误差项的现值和滞后值进行回顾所建立的模型。
ARIMA建模流程
- 序列平稳化( 差分确定)
- p和q的阶数确定(ACF,PACF)
- 建立模型并预测
- 信息准则:BIC
模型选择准则AIC&&BIC
AIC: Akaike information criterion,赤池信息量。
BIC:Bayesian information criterion,贝叶斯信息度量
要解决模型选择的准则问题需要先搞懂似然函数。
百度百科说,似然函数是一种关于统计模型中的参数的函数,表示模型参数中的似然性。
不明觉厉,还是看wikipedia吧
常说的概率是指给定参数后,预测即将发生的事件的可能性。拿硬币这个例子来说,我们已知一枚均匀硬币的正反面概率分别是0.5,要预测抛两次硬币,硬币都朝上的概率:p(HH;p=0.5)
而似然概率正好与这个过程相反,我们关注的量不再是事件的发生概率,而是已知发生了某些事件,我们希望知道参数应该是多少。
现在我们已经抛了两次硬币,并且知道了结果是两次头朝上,这时候,我希望知道这枚硬币抛出去正面朝上的概率为0.5的概率是多少?正面朝上的概率为0.8的概率是多少?
如果我们希望知道正面朝上概率为0.5的概率,这个东西就叫做似然函数,可以说成是对某一个参数的猜想(p=0.5)的概率,这样表示成(条件)概率就是
L(pH=0.5|HH) = P(HH|pH=0.5)
为什么可以写成这样?我觉得可以这样来想:
似然函数本身也是一种概率,我们可以把L(pH=0.5|HH)写成P(pH=0.5|HH); 而根据贝叶斯公式,P(pH=0.5|HH) = P(pH=0.5,HH)/P(HH);既然HH是已经发生的事件,理所当然P(HH) = 1,所以:
P(pH=0.5|HH) = P(pH=0.5,HH) = P(HH;pH=0.5).
右边的这个计算我们很熟悉了,就是已知头朝上概率为0.5,求抛两次都是H的概率,即0.5*0.5=0.25。
所以,我们可以safely得到:
L(pH=0.5|HH) = P(HH|pH=0.5) = 0.25.
这个0.25的意思是,在已知抛出两个正面的情况下,pH = 0.5的概率等于0.25。
再算一下
L(pH=0.6|HH) = P(HH|pH=0.6) = 0.36.
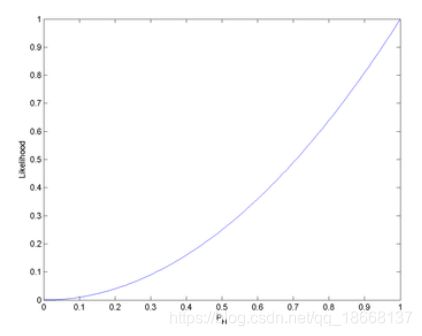
把pH从0~1的取值所得到的似然函数的曲线画出来得到这样一张图:
(来自wikipedia)
可以发现,pH = 1的概率是最大的。
即L(pH = 1|HH) = 1。
那么最大似然概率的问题也就好理解了。
最大似然概率,就是在已知观测的数据的前提下,找到使得似然概率最大的参数值。
这就不难理解,在data mining领域,许多求参数的方法最终都归结为最大化似然概率的问题。
回到这个硬币的例子上来,在观测到HH的情况下,pH = 1是最合理的(却未必符合真实情况,因为数据量太少的缘故)。
说得有点多了哈哈,回到正题。
很多参数估计问题均采用似然函数作为目标函数,当训练数据足够多时,可以不断提高模型精度,但是以提高模型复杂度为代价的,同时带来一个机器学习中非常普遍的问题——过拟合。所以,模型选择问题在模型复杂度与模型对数据集描述能力(即似然函数)之间寻求最佳平衡。
人们提出许多信息准则,通过加入模型复杂度的惩罚项来避免过拟合问题,而AIC和BIC就是来解决这个问题的准则。
AIC是衡量统计模型拟合优良性的一种标准,由日本统计学家赤池弘次在1974年提出,它建立在熵的概念上,提供了权衡估计模型复杂度和拟合数据优良性的标准。
AIC = 2k - 2ln(L)
其中k是模型参数个数,L是似然函数。从一组可供选择的模型中选择最佳模型时,通常选择AIC最小的模型。
当两个模型之间存在较大差异时,差异主要体现在似然函数项,当似然函数差异不显著时,上式第一项,即模型复杂度则起作用,从而参数个数少的模型是较好的选择。当模型复杂度提高(k增大)时,似然函数L也会增大,从而使AIC变小,但是k过大时,似然函数增速减缓,导致AIC增大,模型过于复杂容易造成过拟合现象。目标是选取AIC最小的模型,AIC不仅要提高模型拟合度(极大似然),而且引入了惩罚项,使模型参数尽可能少,有助于降低过拟合的可能性。
BIC贝叶斯信息准则与AIC相似,用于模型选择,
BIC = kln(n) - 2ln(L)
其中,k为模型参数个数,n为样本数量,L为似然函数。kln(n)惩罚项在维数过大且训练样本数据相对较少的情况下,可以有效避免出现维度灾难现象。
训练模型时,增加参数数量,也就是增加模型复杂度,会增大似然函数,但是也会导致过拟合现象,针对该问题,AIC和BIC均引入了与模型参数个数相关的惩罚项,BIC的惩罚项比AIC的大,考虑了样本数量,样本数量过多时,可有效防止模型精度过高造成的模型复杂度过高。
好吧,其实AIC和BIC也有点偏题了,回正题哈哈
看一下怎么用ARIMA咯
首先我们使用ACF和PACF确定ARMA的阶数,进而确定ARIMA的模型参数。第二种方式使用bic选择参数
上代码,首先导入package
import pandas as pd
import pandas_datareader
import datetime
import matplotlib.pylab as plt
from matplotlib.pylab import style
from statsmodels.tsa.arima_model import ARIMA
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf获取茅台的股票数据来分析
start_date = datetime.datetime(2007, 1, 1)
# 指定股票分析截止日期
end_date = datetime.datetime(2019, 3, 1)
# 股票代码
stock_code = '600519.SS' # 沪市贵州茅台
stock_df = pandas_datareader.data.DataReader(stock_code, 'yahoo', start_date, end_date)
# 预览数据
print(stock_df.head())只分析收盘价
stock_all = stock_df.Close
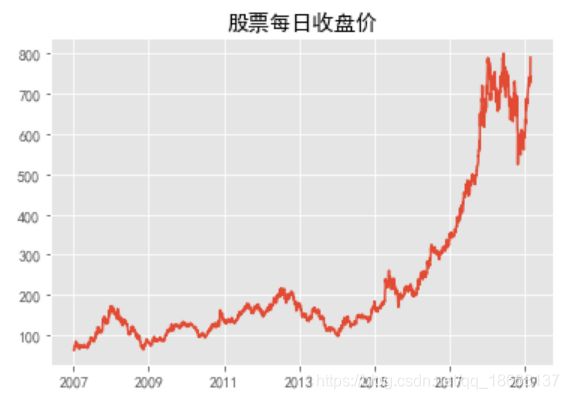
plt.plot(stock_all)
plt.title('股票每日收盘价')
plt.show()数据太多,太远的数据其实没啥用
stock_resample = stock_all.resample('W-MON').mean()
stock_train = stock_resample['2014':'2018']
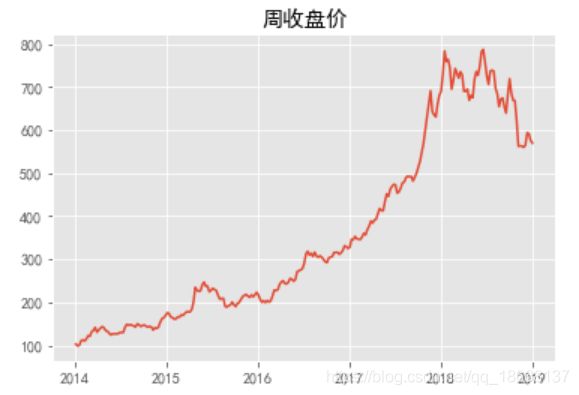
plt.plot(stock_train)
plt.title('周收盘价')
plt.show()自相关图
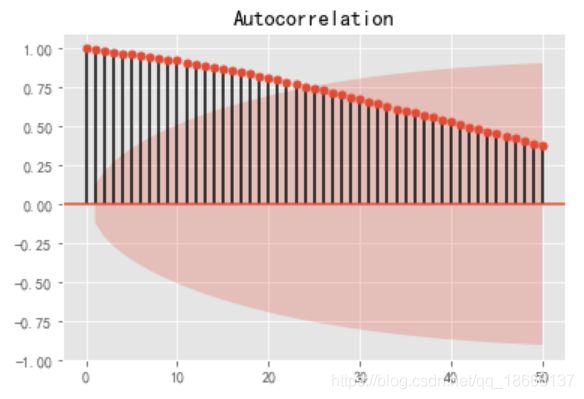
#画出自相关性图
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
plot_acf(stock_train,lags=50)
plt.show()其实从数据图和自相关图就可以看到,数据是非平稳的,检测一下看看
#平稳性检测
from statsmodels.tsa.stattools import adfuller
print('原始序列的检验结果为:',adfuller(stock_train))
#返回值依次为:adf, pvalue p值,usedlag, nobs, critical values临界值 , icbest, regresults, resstore
answer:
原始序列的检验结果为: (-0.9039522834177104, 0.7866680876785267, 15, 245, {'1%': -3.4573260719088132, '5%': -2.873410402808354, '10%': -2.573095980841316}, 1984.5615330766404)看到p-value远远大于0.05,做一下差分吧
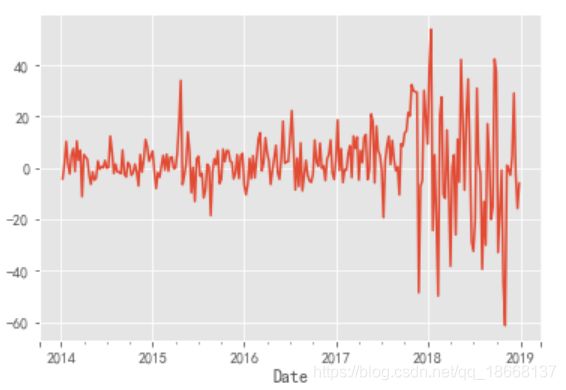
stock_train_diff = stock_train.diff().dropna()
stock_train_diff.plot()
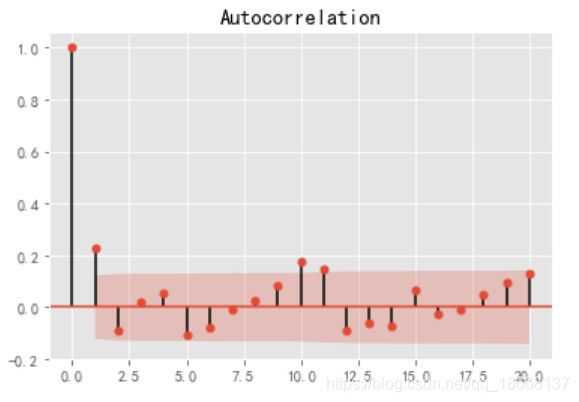
plt.show()好像是平稳了一些窝。画出ACF和PACF图定阶吧
plot_acf(stock_train_diff,lags=20) #画出自相关图
plt.show()
plot_pacf(stock_train_diff,lags=20) #画出偏相关图
plt.show()通过PACF确定p=4,ACF确定q=3
检验结果,p-value达标了,不过差强人意。
print(u'差分序列的ADF 检验结果为: ', adfuller(stock_train_diff)) #平稳性检验
#一阶差分后的序列的时序图在均值附近比较平稳的波动, 自相关性有很强的短期相关性, 单位根检验 p值小于 0.05
所以说一阶差分后的序列是平稳序列#对一阶差分后的序列做白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
print(u'差分序列的白噪声检验结果:',acorr_ljungbox(stock_train_diff, lags= 1)) #返回统计量和 p 值
# 差分序列的白噪声检验结果:(array([13.84221767]), array([0.00019882])) p值为第二项,最后拟合模型并预测,把预测结果和训练数据结合concat
model = ARIMA(stock_train,(4,1,3)).fit()
pre = model.forecast(len(stock_resample['2019':]))[0]
pre_result = pd.Series(pre,index = stock_resample['2019':].index)
result_1 = pd.concat([stock_train,pre_result],axis = 0)第二种方法是使用bic对模型进行定阶
#对模型进行定阶
from statsmodels.tsa.arima_model import ARIMA
pmax = 5 #一般阶数不超过 length /10
qmax = 5
bic_matrix = []
for p in range(pmax +1):
temp= []
for q in range(qmax+1):
try:
temp.append(ARIMA(stock_train_diff, (p, 1, q)).fit().bic)
except:
temp.append(None)
bic_matrix.append(temp)
bic_matrix = pd.DataFrame(bic_matrix) #将其转换成Dataframe 数据结构
p,q = bic_matrix.stack().idxmin() #先使用stack 展平, 然后使用 idxmin 找出最小值的位置
print(u'BIC 最小的p值 和 q 值:%s,%s' %(p,q)) # BIC 最小的p值 和 q 值:0,2同样地,拟合模型并预测
model2 = ARIMA(stock_train,(p,1,q)).fit()
pre2 = model2.forecast(9)[0]
pre_result2 = pd.Series(pre2,index = stock_resample['2019':].index)
result_2 = pd.concat([stock_train,pre_result],axis = 0)最后,画图,看看两种方法选择的阶数拟合的模型预测效果如何
plt.plot(result_1,c = 'r')
plt.plot(stock_resample['2019':],c = 'b')
plt.show()
plt.plot(result_2,c = 'r')
plt.plot(stock_resample['2019':],c = 'b')
plt.show()说实话,好像基本一样,可能是本身模型预测效果就不好,这里也没做很多的数据处理,具体问题,再想想吧哈哈