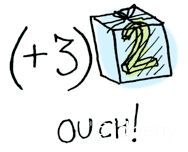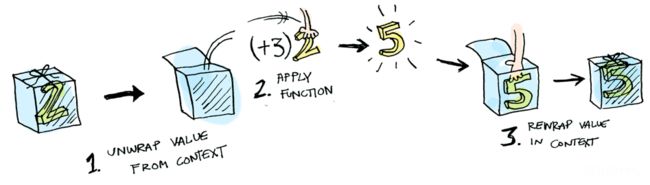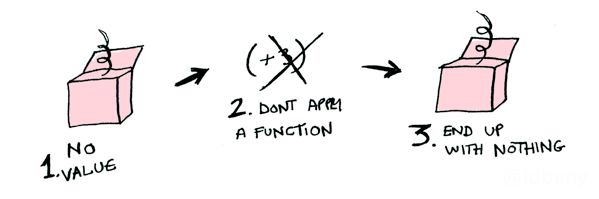Swift系列三十二 - 函数式编程

函数式编程（Funtional Programming，简称FP）是一种编程范式，也就是如何编写程序的方法论。

一、什么是函数式编程？

1.1. 介绍

主要思想： 把计算过程尽量分解成一系列可复用函数的调用。
主要特征： 函数是"一等公民"（函数与其他数据类型一样的地位，可以赋值给其他变量，也可以作为函数参数、函数返回值）。

函数式编程中几个常用的概念：

• Higher-Order Function、Function Currying
• Functor、Applicative Functor、Monad

延伸：函数式编程最早出现在LISP语言，绝大部分的现代编程语言也对函数式编程做了不同程度的支持，比如JavaScript、Python、Swift、Kotlin、Scala等。

1.2. 实践

1.2.1. 传统写法

示例代码：

var num = 1
func add(_ v1: Int, _ v2: Int) -> Int {
      v1 + v2 }
func sub(_ v1: Int, _ v2: Int) -> Int {
      v1 - v2 }
func multiple(_ v1: Int, _ v2: Int) -> Int {
      v1 * v2 }
func divide(_ v1: Int, _ v2: Int) -> Int {
      v1 / v2 }
func mod(_ v1: Int, _ v2: Int) -> Int {
      v1 % v2 }

// [(num + 3) * 5 - 1] % 10 / 2
print(((num + 3) * 5 - 1) % 10 / 2) // 输出：4
var result = divide(mod(sub(multiple(add(num, 3), 5), 1), 10), 2)
print(result) // 输出：4

看到上面的嵌套非常多，如果遇到复杂的场景，整个代码可读写非常差。

1.2.2. 函数式写法

如果把add函数赋值给一个变量，函数固定加一个数，函数式写法就很方便。

示例代码；

func add(_ v: Int) -> (Int) -> Int {
      {
     $0 + v} }
var addFn = add(3)
print(addFn(5)) // 输出：8
print(addFn(20)) // 输出：23
print(addFn(66)) // 输出：69

add()返回一个函数，调用返回的函数时也可以传入一个参数，最终结果是把这两个参数加起来。而且这样子可以做到函数可复用。

同理，其他函数也是这样函数式处理：

typealias FnInt = (Int) -> Int
func add(_ v: Int) -> FnInt {
      {
     $0 + v} }
func sub(_ v: Int) -> FnInt {
      {
     $0 - v} }
func multiple(_ v: Int) -> FnInt {
      {
     $0 * v} }
func divide(_ v: Int) -> FnInt {
      {
     $0 / v} }
func mod(_ v: Int) -> FnInt {
      {
     $0 % v} }

let fn1 = add(3)
let fn2 = multiple(5)
let fn3 = sub(1)
let fn4 = mod(10)
let fn5 = divide(2)

let result = fn5(fn4(fn3(fn2(fn1(num)))))
print(result) // 输出：4

发现如果使用上面的写法，代码依然看起来很臃肿。下面介绍函数合成，可以解决此问题。

二、函数合成

函数合成，其实就是把多个函数合成到一个函数里面。

示例代码（函数合成）：

func composite(_ f1: @escaping FnInt, _ f2: @escaping FnInt) -> FnInt {
     
    {
      f2(f1($0)) }
}
let fn = composite(add(3), multiple(5))

这样就把加法和乘法的函数合成到一个函数了，其他函数同理。如果想要函数更加优雅，我们可以自定义运算符。

示例代码（自定义运算符）：

infix operator >>> : AdditionPrecedence
func >>>(_ f1: @escaping FnInt, _ f2: @escaping FnInt) -> FnInt {
     
    {
      f2(f1($0)) }
}
let fn = add(3) >>> multiple(5) >>> sub(1) >>> mod(10) >>> divide(2)
let result = fn(num)
print(result) // 输出：4

执行fn(num)最开始进入的是f1，而f1的函数返回值就是f2的参数值，所以这两个地方的参数类型一定是一致的。

为了保证函数的可复用性，使用泛型进行表述：

func >>> <A, B, C> (
    _ f1: @escaping (A) -> B,
    _ f2: @escaping (B) -> C)
    -> (A) -> C {
     
    {
      f2(f1($0)) }
}

三、高阶函数

高阶函数是至少满足下列一个条件的函数：

• 接受一个或多个函数作为输入（例如：map、filter、reduce等）
• 返回一个函数

在FP中到处都是高阶函数。例如上面示例代码中的add、sub、multiple、divide、mod。

四、柯里化

什么是柯里化（Currying）？
将一个接受多参数的函数变换为一系列只接受单个参数的函数。

示例代码一（基础代码）：

func add(_ v1: Int, _ v2: Int) -> Int {
      v1 + v2 }
add(10, 20)

示例代码二（柯里化）：

func add(_ v: Int) -> (Int) -> Int {
      {
     $0 + v} }
add(10)(20)

// 原函数接收两个参数的柯里化
func currying<A, B, C>(_ fn: @escaping (A, B) -> C)
    -> (B) -> (A) -> C {
     
    {
     
        b in {
     
            a in fn(a, b)
        }
    }
}
currying(add)(20)(10)

// 重载~运算符
prefix func ~<A, B, C>(_ fn: @escaping (A, B) -> C)
    -> (B) -> (A) -> C {
     
    {
     
        b in {
     
            a in fn(a, b)
        }
    }
}
let fn = (~add)(3) >>> (~multiple)(5) >>> (~sub)(1) >>> (~mod)(10) >>> (~divide)(2)
print(fn(1)) // 输出：4

示例代码一到示例代码二的过程就是柯里化。而且使用通用柯里化函数后，柯里化同类型原函数时只需要调用通用柯里化函数就可以。

Array、Optional的map方法接收的参数就是一个柯里化函数。

示例代码三（原函数接收三个参数的柯里化）：

func add1(_ v1: Int, _ v2: Int, _ v3: Int) -> Int {
      v1 + v2 + v3 }

// add1柯里化
func add2(_ v3: Int) -> (Int) -> (Int) -> Int {
     
    // v2 == 20
    return {
      v2 in
        // v1 == 10
        return {
      v1 in
            return v1 + v2 + v3
        }
    }
}
add2(30)(20)(10)

// 原函数接收三个参数的柯里化
func currying<A, B, C, D>(_ fn: @escaping (A, B, C) -> D)
    -> (C) -> (B) -> (A) -> D {
     
    {
     
        c in {
     
            b in {
     
                a in fn(a, b, c)
            }
        }
    }
}
currying(add2)(30)(20)(10)

注意：柯里化函数参数一般是原函数参数的倒序方式。具体需要根据开发需求调整对应参数顺序。

五、函子

像Array、Optional这样支持map运算的类型，称为函子（Functor）。

Array中map的定义：

public func map<T>(_ transform: (Element) throws -> T) rethrows -> [T]

Element是数组内部存放的实体，map函数返回值类型是数组，闭包表达式返回值和数组内部存放的实体都是泛型T。满足函子定义的条件。

Optional中map的定义：

public func map<U>(_ transform: (Wrapped) throws -> U) rethrows -> U?

Wrapped是可选类型内部存放的实体，map函数返回值类型是可选类型，闭包表达式返回值和数组内部存放的实体都是泛型U。满足函子定义的条件。

比如有一个可选类型，内部包装的是2，如果要进行+3操作，则需要把数字2先解包，+3操作完成后把结果再放回包装盒内（可选类型），如果盒子是空的，则不作任何操作。下面是图例：

第一步：取值

第二步：操作再包装

第三步：空值不处理

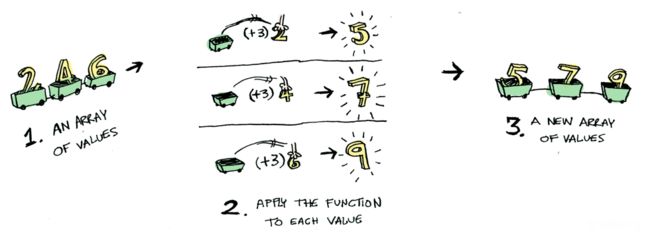
数组map图例（遍历每一个值，完成后的值放到新的数组里）：

5.1. 适用函子

对任意一个函子F，如果能支持以下运算，该函子就是一个适用函子（Application Functor）。

// 传入任意泛型参数A，最终返回对应类型，该类型的实体
func pure<A>(_ value: A) -> F<A>
func <*><A, B>(fn: F<A -> B>, value: F<A>) -> F<B>

Optional可以成为适用函子：

func pure<A>(_ value: A) -> A? {
      value }
infix operator <*> : AdditionPrecedence
func <*><A, B>(fn: ((A) -> B)?, value: A?) -> B? {
     
    guard let f = fn, let v = value else {
      return nil }
    return f(v)
}

var value: Int? = 10
var fn: ((Int) -> Int)? = {
      $0 * 2}
print(fn <*> value as Any) // 输出：Optional(20)

Array可以成为适用函子：

infix operator <*> : AdditionPrecedence
func pure<A>(_ value: A) -> [A] {
      [value] }
func <*><A, B>(fn: [(A) -> B], value: [A]) -> [B] {
     
    var arr: [B] = []
    if fn.count == value.count {
     
        for i in fn.startIndex..<fn.endIndex {
     
            arr.append(fn[i](value[i]))
        }
    }
    return arr
}
print(pure(10)) // 输出：[10]

var arr = [{
      $0 * 2 }, {
      $0 + 10 }, {
      $0 - 5 }] <*> [1, 2, 3]
print(arr) // 输出：[2, 12, -2]

5.2. 单子

对任意一个类型F，如果能支持以下运算，那么就可以称为是一个单子（Monad）。

func pure<A>(_ value: A) -> F<A>
func flatMap<A, B>(_ value: F<A>, _ fn: (A) -> F<B>) -> F<B>

很显然，Array、Optional都是单子。

注意：有些参考资料会说单子就是函子。

参考资料：

• https://adit.io/posts/2013-04-17-functors,_applicatives,_and_monads_in_pictures.html

• http://www.mokacoding.com/blog/functor-applicative-monads-in-pictures