[数据结构与算法] 串,数组和广义表

第四章 串、数组和广义表

4.1 串的定义

串(String)– 零个或多个任意字符组成的有限序列

• 字串:一个串中任意个连续的字符组成的子序列(含空串)称为该串的子串.
  • 相当于子集
• 真子串:是指不包含自身的所有子串
  • 真子集
• 主串: 包含子串的串相应地称为珠串
• 字符位置 字符在序列中的序号为该字符在串中的位置
• 空格串: 由一个或多个空格组成的串 与子串不同
• 串相等: 当且仅当两个串的长度相等,并且各个对应位置上的字符都相同的时候,这两个串才是相等的.
  • 所有空串是相等的

4.2 案例引入

串的运用非常广泛,计算机上的非数值处理的对象大部分是字符串数据,例如:文字编辑,符号处理,各种信息处理系统等.

案例1: 病毒感染检测

• 研究者将人的DNA和病毒的DNA都表示成由一些字母组成的字符串序列
• 然后检测某种病毒DNA序列是否出现在患者的DNA序列里面,如果出现过,则此人感染了这个病毒
• 例如:假设病毒的DNA序列为baa,患者1的DNA序列为aaabbba,则感染,患者2的DNA序列为babbba,则未感染(注意 人的DNA序列是线性的,但是病毒的DNA是环状的)
• 

可以看出,字符串查找很重要,为我们的生活带来了很大的便捷

4.3 串的类型定义,存储结构及运算

4.3.1 串的类型定义

串中的元素逻辑关系与线性表相同,可以采用与线性表相同的存储结构

4.3.2 串的存储结构

物理上的元素的逻辑关系与逻辑上的元素关系一致(不需要额外的指针来表示出串的顺序)

串的顺序存储结构

#define MAXLEN 255

typedef struct{
    char ch[MAXLEN + 1];//储存串的一维数组,0号位置闲置不用,这里一定要是字符型
    
    int length;//串的当前长度
    
}SString

如果我们只用用于存储而不频繁的插入和删除,那么我们就使用这个存储结构的串

串的链式存储结构

优点: 操作方便 缺点: 存储密度低(1/(1+4)=0.2)

还有一种方法,可以大大提高存储密度(4/(4+4) = 0.5)

这里的结点中的数据域可以叫做存储块

因此我们常用下面这种链式存储结构----块链结构

#define CHUNKSIZE 80;//块的大小可由用户定义

typedef struct Chunk{
    char ch[CHUNKSIZE];
    struct Chunk *next;
}Chunk;//结点

typedef struct{
    Chunk *head,*tail;
    
    int curlenl;
}LString //字符串的块链结构

4.3.3 串的模式匹配算法

算法目的：

​ 确定主串中所含的字串第一次出现的位置（定位）

算法应用：

• 搜索引擎，拼写检查，语言翻译，数据压缩

算法种类

• BE算法（Brute-Force，又称古典的，经典的，朴素的，穷举的）
• KMP算法（特点：速度快）

BF算法

简称简单匹配算法。采用穷举法的思想

最重要的思想就是回溯

• i和j逐个比较，如果不匹配的话，进行回溯（j回到第一个，i在最开始比较的地方进一位）

匹配成功： 返回i - T.length

Index(S,T,pos)

• 将字串的第pos个字符和模式串的第一个字符比较
• 若相等,逐个比较后续字符
• 若不想等,进行回溯,模式串重新归回第一个

算法实现

int Index_BF(SString s,SString t){
    int i=1,j =1;
    
    while(i<=S.length && j<=T.length){
        if(s.ch[i] == t.ch[h]){++i;++j}
        else {i = i-j+2; j =1}//回溯
    }
    if(j >= T.length) return i-t.length;
    else return 0;
}

BF算法的时间复杂度

KMP算法

由三个科学家共同提出,三个名字的简称\

​ 时间复杂度做了改进,变为O(n+m)

利用已经部分匹配的结果而加快串的滑动速度

主串S的指针i不必回溯! 可提速到O(n+m)

为此,我们定义了next[i]函数,表明当模式中第j个字符与主串中相应字符"失配"时,在模式中需要重新和主串中该字符进行比较的字符的位置

举例:

算法实现:

int Index_KMP (SString S,SString T,int pos){
    int i = pos; int j =1;
    while(i < S.length && j < T.length){
        if(j==0 || S.ch[i] == T.ch[i]){ 
            i++;
            j++;
        }else{
            j = next[j]; //算法改进的点睛之笔
        }
    }
    if(j > T.length) return i - T.length;
    
    else return 0;
    
}

next函数的改进

• 有时候,会发生一些尴尬的情况,如图所示

• 

• 函数会没有意义的重复执行多次,造成了很大的时间上的浪费

-

4.4 数组

数组: 按一定格式排列起来的具有相同类型的数据元素的集合.

• 一维数组: 若线性表中的数据元素为非结构的简单元素,则称为一维数组

  • 一维数组的逻辑结构: 线性结构.定长的线性表

• 二维数组: 若一维数组中的数据元素又是一维数组结构,则称为二维数组.

  • 二维数组的逻辑结构**(两种看法**):
    • 非线性结构(抽象的角度): 每个数据元素既在一个行表中,又在一个列表中(每个元素不止有一个前驱和一个后继)
    • 线性结构定长的线性表(实际上建立的情况): 该线性表中的每个数据元素也是一个定长的线性表
  • 声明格式: 数据类型 变量名称[行数][列数]

• 三维数组: 若二维数组中的元素又是一个一维数组,则称为三维数组 以此类推

结论:

• 线性表结构是数组结构的一个特例
• 而数组结构又是线性表结构的拓展

数组特点:

• 结构固定—定义之后,数组的维数和维界都不再改变

数组的基本操作

• 初始化,销毁,修改,取元素

4.4.1 数组的抽象数据类型定义

n维数组的抽象数据类型

二维数组举例

4.4.2 数组的顺序存储

根据数组的特点,我们一般就是使用顺序存储结构来表示数组

注意:

• 数组可以是多维的,但是储存元素的内存地址是一维的,因此,我们在存储数组结构之前,我们要解决将多维关系映射到一维关系的问题

一维数组存储方法就不说了,懂的都懂

二维数组的存储方法

两种方法

• 以行序为主序(低下标优先)C,JAVA,BASIC,COBOL和PASCAL

举例

• 以列序为主序(高下表优先)

三维数组存储方式

​ 按页\行\列存放,页优先的顺序存储

4.4.3 特殊矩阵的压缩存储

矩阵: 一个由m*n个元素排成的m行n列的表

矩阵的常规存储: 将矩阵描述为一个二维数组

矩阵常规存储的特点:

• 可以对其元素进行随机存取
• 矩阵运算非常简单:存储密度为1

不适宜常规存储的矩阵: 值相同的元素很多且呈某种规律分布

矩阵的压缩存储: 为多个相同的非零元素只分配一个存储空间;0元素不分配空间

FAQ

1. 什么样的矩阵能够进行压缩?
   • 一些特殊的矩阵: 如: 对称矩阵,对角矩阵,三角矩阵,稀疏矩阵等等
2. 什么叫稀疏矩阵?
   • 矩阵中非零元素的个数较少

对称矩阵

特点: 在n*n的矩阵中,满足 Aij = Aji

存储方法: 只存储上三角或下三角的数据元素.共占用n(n+1)/2个元素空间

存储结构: 可以以行序作为主序将元素存放在一个一维数组sa[n(n+1)/2]当中,算法就是利用等差数列和

三角矩阵

**特点: ** 对角线以下(或者以上)的数据元素全都是常数

存储方法: 重复元素c共享一个元素存储空间,共占用n(n+1)/2 +1 个空间

对角矩阵

存储方法: 以二维数组的方法存储

稀疏矩阵

储存方法: 建立一个数组保存元素,数组的元素是一个三元组

三元组顺序表

上图0元素可以加入一些信息,(总行数,总列数,总个数)

三元组顺序表又称为有序的双下标法

三元组的顺序表的优点: 非零元素在表中按行序有序存储,因此便于进行依次顺序处理的矩阵运算

三元组顺序表的缺点: 不能随机存取. 若是按行号存取某一行中的非零元,则需从头开始进行查找

十字链表

• 优点: 它能够灵活地插入因运算而产生的新的非零元素,删除因运算而产生的新的零元素,实现矩阵的各种运算

• 在十字链表中,矩阵的每一个非零元素用一个结点表示,该结点除了三元组的那三个之外,还有两个域:

  • right: 用于链接同一行中的下一个非零元素
  • down: 用于链接同一列中的下一个非零元素
    

• 这个链表我们还需要额外建立两个指针域,一个是指向行的指针域,一个是指向列的指针域

举例:

4.5 广义表

简介

广义表(Lists)是n>=0个元素组成的有限序列,其中每一个元素可能是一个原子,也可能是一个广义表

说人话就是,数据类型可以不同,元素放数组也可以,里面想放什么就放什么

举例:

• 广义表通常记作: LS = (a1,a2…,an)
  • 其中LS为表名, n为表的长度,每一个ai为表的元素
• 习惯上,一般用大写字母表示广义表,用小写字母表示原子
• 表头,广义表的第一个元素就是表头
• 表尾: 除表头外的其他元素组成的表.
  • 记作: tail(LS) = ( a2,a3,…,an)
• 表头和表尾是可以重合的(当有一个元素的时候)

举例:

广义表的性质

1. 广义表中的数据元素有相对次序;一个直接前驱和一个直接后继

2. 广义表的长度定义为最外层所含元素的个数

3. 广义表的深度定义为该广义表展开后所含括号的重数

   1. 原子的深度是0,表的深度是1
   2. 例子:

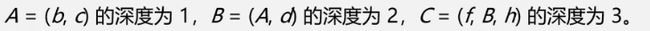
4. 广义表可以为其他广义表共享(就是可以套娃引用)

5. 广义表可以是一个递归的表(递归的深度是无穷值,但是长度是有限值)

6. 广义表是多层次的结构(就是里面怎么放都行)

广义表和线性表的区别?

广义表可以看成是线性表的推广, ** 线性表是广义表的特例**

• 广义表的结构相当灵活,它可以兼容线性表,数组,树和有向图等各种常用的数据结构
• 当二维数组的每行或每列作为子表处理时,二维数组即为一个广义表

广义表的基本运算

616839023836)]

广义表的性质

1. 广义表中的数据元素有相对次序;一个直接前驱和一个直接后继
2. 广义表的长度定义为最外层所含元素的个数
3. 广义表的深度定义为该广义表展开后所含括号的重数
   1. 原子的深度是0,表的深度是1
   2. 例子:[外链图片转存中…(img-lf1Sv5xv-1616839023838)]
4. 广义表可以为其他广义表共享(就是可以套娃引用)
5. 广义表可以是一个递归的表(递归的深度是无穷值,但是长度是有限值)
6. 广义表是多层次的结构(就是里面怎么放都行)

广义表和线性表的区别?

广义表可以看成是线性表的推广, ** 线性表是广义表的特例**

• 广义表的结构相当灵活,它可以兼容线性表,数组,树和有向图等各种常用的数据结构
• 当二维数组的每行或每列作为子表处理时,二维数组即为一个广义表

广义表的基本运算