西瓜书重温(二): 模型评估与选择
1. 写在前面
寒假在家的时间想重新阅读周志华老师的《机器学习》, 第一是找工作需要,第二是内在驱动,自己也确实想学习关于算法的一些底层知识了, 吴军老师在《数学之美》里面说: “技术分为道和术两种, 具体的做事方法是术, 做事的原理和原则是道, 追求术的人一辈子工作很辛苦,而只有掌握了事情的本质和精髓才能在工作中游刃有余”, 西瓜书我觉得应该就是道的层面去总结机器学习, 虽然我感觉这本书对初学者不是很友好 ,因为我第一次读这本书的时候是上一年比这早些时候, 那时候给我的体会是完全不知所云或者是停留在皮毛根本无法深入,即使理解了某些算法的公式推导,所以我并没有耐心看,感觉还不如吴恩达老师的课听得爽哈哈(那时候我并不知道原来机器学习这样学,只是停留在了门槛,连入门都不太算)。所以基于吴恩达老师的课, 这一年来通过一些项目和比赛,慢慢的用上了机器学习,期间时常窃喜原来机器学习算法也不是多么难嘛,调个包就实现了呀,直到一年后的现在,由于面试需要,我又不得不重新揭开这本书读的时候,才真正的发现了这本书的魅力,虽然目前只看完了第二章,但真的令我折服,也认识到了之前的无知, 仅仅掉包和使用这只能算ML的术,但讲真有些时候我根本不知道为啥要这么用,别人问我,也总是喜欢给它一个优雅的名字叫做“trick”或者称为“玄学”,但我通过这次读发现, 有些东西根本就不是玄学或者所谓的trick, 人家背后都有很强大的理论支撑,还有就是学习的算法目前也只是术层,根本不会结合着业务或算法原理去了解背后的所以然。所以现在学习的感觉就是知识和要做的项目越多,心里就越没有底,不踏实,毕竟玄学和trick不能陪伴我们太长。直到这次重新阅读西瓜书, 才慢慢的开始释然,也让我对机器学习有了新的认知。 所以接下来的这段时间,会重新阅读西瓜书,然后把里面的重要思想(原理层面),学习的笔记,还有通过这一年的实践对知识点的新理解等进行记录, 把知识进行沉淀, 后期再通过实践不断的补充, 真正去练一波算法内功 。
这篇文章对应《西瓜书》的第二章, 花了三个大晚上,终于把第二章啃完,给我的整体感觉就是醍醐灌顶,有点打通任督二脉。初读不知书中意,再读已是书中人哈哈, 果真,这种好书,随着知识的积累和实践,每次读都会发现新东西,当然也发现,通过练术,才能不断的得道。有点扯远了, 开始回归正文。这一篇是模型评估和选择,对应西瓜书第二章内容,下面依然是先梳理逻辑, 因为这一章概念很多,得先理清楚到底每一节说了一个啥事,各节之间有个什么样的联系,这样才能把知识拎起来。
第一节首先会介绍经验误差与过拟合是怎么回事, 在现实任务中,往往我们会有多种模型可选,即使一种模型也会有多种参数可调, 那么我们该怎么选择呢? 这时候我们往往通过评估模型的泛化误差,因为我们希望训练的模型泛化能力好,也就是希望在新样本上表现的很好。而通过第一节会发现我们不能得到泛化误差,那么这个泛化误差怎么衡量呢?
第二节评估方法给出了答案,通常我们可通过实验测试来对学习器的泛化误差进行衡量,具体做法是从数据集中划分出一个测试集出来,然后用测试集上的判别效果来估计模型在实际使用中的泛化能力,那这个过程又出来两个问题:①应该如何合理的划分数据集? ②判别效果又怎么度量,也就是用什么样的评价标准? 划分数据集有不同的方式,第二节会给出。
第三节性能度量给出了问题②的答案,不同的任务有不同的性能度量, 书中主要是以分类问题的性能度量进行展开,会学习所熟知的错误率,精度,查准率查全率, F1, ROC与AUC, 代价敏感错误率与代价曲线, 这几个具体是干啥的我们得知道,查准率和精度比较简单,给定一个数据集,给定确定的模型和阈值(大于这个值我预测为正例,小于这个值我预测反例),就很容易的做出预测,然后对比真实label就能计算, 但在类别极度不平衡的时候参考的意义不大,因为这种情况下模型只预测类别很多的那个类就能达到很好的精度,但显然没有意义。 于是乎,又出来了查准率,查全率,要求模型不仅能预测的准还要全, 但这俩往往矛盾,后面会拿个例子直观感受, 不能很好的“双高”,于是乎为了进行这俩的权衡,出了个F1进行调和平均这俩策略。 但要注意上面几个性能度量计算的前提训练集定了下来,模型的阈值定了下来,如果模型的阈值选择不同,我们就会得到不同的上面那些性能度量,这时候我们应该怎么选择模型呢? 这时候就会用到ROC/AUC或者PR曲线,往往我们希望选择的模型AUC更大。 而有时候我们又往往遇到一种问题,模型犯得不同错误所造成的的后果会不同,比如医疗诊断里面,模型把一个健康人预测成病人无非增加了进一步检查的麻烦,而如果把一个病人预测成健康人就可能错过了拯救生命的最佳时机,这时候后面这种代价我们一般是承受不起的,于是必须对这两种错误率加权, 这时候就会面临着非均等代价下的模型评估和阈值选择问题,代价曲线就可以帮助我们完成这个事情。
第四节比较检验讨论的一个问题是上面我们是用了一个测试集, 也用了各种性能度量评估出了我们的模型, 那么我们真的就能根据这个性能度量比较模型进行选择了吗? 我们可能忽视了一个问题,就是测试集也是在真实情景中采样出来的呀,我们怎么能够保证模型在这个测试集上的性能就接近于在真实世界数据里面的性能, 测试集的采样就不会出现偏差吗? 于是乎还得做一波统计假设检验,看是否能够通过上面的抽样测试来拒绝或者接受我们在真实世界中的做出的性能假设。
第五节方差和偏差是在解释泛化性能, 也就是上面我们通过实验估计出了模型的泛化性能, 也通过假设验证了这种泛化性能, 但模型为什么会出现这样的泛化性能呢? 这里会通过泛化误差的分解给出最后的具体答案,也帮助我们真正的理解为啥过拟合是方差大,需要解决方差问题,欠拟合是偏差大,需要解决偏差的问题了。
通过上面的梳理,希望能对第二章有个宏观的把握了, 下面就开始整理每一节的笔记了, 这篇文章依然是会超级长,光上面的逻辑串一遍都这么长了,如果再加上某个点细化,然后举例子辅助理解,尤其是AUC和代价敏感曲线那,西瓜书本身写的并不是很好理解,这一块得加一些例子和代码辅助操作,所以通篇下来,篇幅会很长,毕竟我也是方便以后复习的时候方便查阅, 都整理到一块,更成体系一些。 当然,还是各取所需即可哈哈
大纲如下:
- 经验误差与过拟合(这个简单的说几个概念,经验误差,泛化误差)
- 评估方法(这里面主要是划分数据集的三种方法,留出,交叉验证,自助和验证集的来历)
- 性能度量(分类任务常用的性能度量:错误率,精度,查准率查全率, F1, ROC与AUC, 代价敏感错误率与代价曲线)
- 比较检验(建设检验)
- 方差与偏差(泛化误差分解)
Ok, let’s go!
2. 经验误差与过拟合
这里面主要是知道几个关于误差的概念,所谓误差,就是学习器的实际预测输出与样本的真实输出之间的差异, 而误差又有经验误差和泛化误差之分:
- 经验误差: 也称训练误差, 是学习器在训练集上的误差
- 泛化误差: 学习器在新样本上的误差
显然,我们希望学习器的泛化误差小,而我们一开始,是不知道新样本长什么样,所以先想办法把训练误差降下来, 但这个学习的过程中,如果不把握好一个度,就很容易使得模型过分的去学习训练集的数据特点,这样很可能把训练样本自身的一些特点当做所有潜在样本都会具有的一般性质,导致如果将模型用于一个没有见过的新数据集, 模型预测的时候反而会产生犹豫,从而不能很好的预测新数据,也就是泛化能力(预测新数据的能力)下降,这种现象就在ML中称为过拟合现象。而显然,我们其实是希望模型在训练集里面学习潜在样本间的那种”普遍规律“,然后将这种规律用到新数据上,做出正确的预测。
所以在实际应用中模型学习的这个度把握是个难点,是我们重点要思考的东西,也就是学习到啥程度算是学习到了“普适规律”? 学习过了,就容易过拟合, 学习不好, 又容易学不到训练样本中的一般性质, 这种现象在ML中称为欠拟合, 与过拟合对应。周老师给了一个过拟合与欠拟合的对应感觉非常形象:
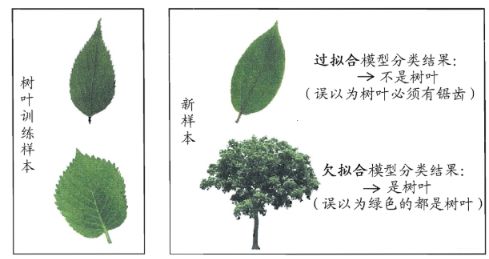
那么如何才能在实际中把握好这个学习的”度“呢? 首先得先明白过拟合和欠拟合发生的原因, 对于过拟合, 一般的原因就是学习器学习能力太强大,可观层面就是模型太复杂了, 以至于把训练集特有的那部分特点也学习到了; 而欠拟合,一般是模型学习能力不足, 这个一般好办,加大模型的复杂程度就可以解决,比如神经网络的话增加层数或神经单元个数,决策树的话增加分支,叶子,深度等,增加训练轮数等,而比较难办的就是过拟合, 如果你说, 这怎么难办了? 欠拟合了你增加模型复杂度,那过拟合来减少模型复杂度啊, 减少上面的那些不就行了? 哈哈,哪有这么简单, 咱又没有上帝的视角,咱知道要减少多少才正好, 减少的太多不就又欠拟合了? 这就又出来一个度的问题, 所以针对这个问题上, 各个模型又会有各种缓解过拟合的策略,比如正则呀,Dropout或者对叶子或分支约束啊等等,如果条件允许,加大数据集是更好的方法。注意这里是缓解而不是避免,这东西避免不了。
那么如何才能把握好这个度呢? 常用的策略就是监控学习器的学习过程, 一般会画模型的学习曲线, 类似于下面这种:

这样能够判断出啥时候模型是欠拟合,啥时候模型会过拟合, 只要我们知道了当前模型的问题,就可以采取相应的措施进行调整。 而这东西怎么看呢? 这个就会引出方差和偏差的概念, 这个具体的第五部分再详细看看。 总之有了这个东西,我们能判断出模型的学习状态,就可以采取相应措施进行调整。
下面再引出一个问题,就是模型的选择了,就像前面提到的, 对于某个任务,往往会有多种模型算法可供选择,即使一种模型, 不同的调参也会有不同的模型, 这时候,我们应该如何进行选择呢? 这就是ML中的模型选择问题,理想的方案就是对候选模型的泛化误差评估, 然后选择泛化误差较小的, 但是我们根本无法直接获得泛化误差,于是乎我们需要一些评估方法。
3. 评估方法
通常,我们是通过实验测试的方法对学习器的泛化误差进行评估,简单的做法就是从数据集里面划分出一部分“测试集”, 这部分模型不能见, 先用剩下的进行训练,然后用这个测试集测试,得到测试误差作为泛化误差的近似。 那么如何划分出这部分测试集,以及如何测试又成了一门学问。下面介绍了常用的三种方法:
3.1 留出法
这个非常简单,假设数据集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) . . . } D=\{(x_1,y_1), (x_2, y_2)...\} D={ (x1,y1),(x2,y2)...},有 m m m个样本, 留出法就是直接将 D D D分成两个互斥的集合,其中一个作为训练集 S S S, 另一个作为测试集 T T T, 这两个不能有交集,且并集就是整个数据集。 sklearn中的train_test_split函数就是做这个东西的。一般常用的划分比例6:4,7:3, 8:2等。
但是划分的时候注意一些问题, 第一个就是训练集/测试集划分要保证数据分布一致性,避免因数据划分过程引入额外的偏差对最终结果产生影响。 尤其是分类的数据, 这时候划分的时候要保持样本的类别比例相似, 比如一共1000个样本,500个正,500个负,按照7:3的比例划分数据集, 训练集700, 测试集300, 这时候划分的时候要保证两个数据集里面正负样本的比例,即需要分层抽样,即训练集里面的正负个数 ( 500 ∗ 7 / 10 , 500 ∗ 7 / 10 ) (500*7/10, 500*7/10) (500∗7/10,500∗7/10), 测试集里面的正负个数 ( 500 ∗ 3 / 10 , 500 ∗ 3 / 10 ) (500*3/10, 500*3/10) (500∗3/10,500∗3/10), 这个比例的计算可以用pandas的value_counts()乘以比例得到训练集和测试集里面正负样本的个数。划分的时候可以用sklearn的StratifiedShuffleSplit函数。 如果训练集和测试集样本类别比例差异很大,则误差估计将由于训练/测试数据的分布差异产生偏差。
另一个问题就是这样即使确定出了训练集和测试集的样本比例, 仍然存在多种划分方式对数据集分割,比如把D中的样本排序,然后取前350个正例放入训练集, 也可以取后350个正例放入训练集, 不同的划分方式又可以对模型评估产生影响。 所以, 单次使用留出法得到的估计结果往往不够稳定可靠, 使用留出法的时候,一般采用若干次随机划分, 重复进行实验评估然后取平均作为最终的结果。
3.2 交叉验证法
这个是将数据集D划分为 k k k个大小相似的互斥子集, D = D 1 ∪ D 2 ∪ … ∪ D k , D i ∩ D j = ∅ ( i ≠ j ) D=D_{1} \cup D_{2} \cup \ldots \cup D_{k}, D_{i} \cap D_{j}=\varnothing(i \neq j) D=D1∪D2∪…∪Dk,Di∩Dj=∅(i=j), 每个子集 D i D_i Di都尽可能保持数据分布一致性, 即从 D D D中通过分层抽样得到。 在一些比赛中,常常会见到这个操作:
from sklearn.model_selection import StratifiedKFold
skf = StratifiedKFold(n_split=10) # 10折交叉验证
for k, (trn_index, te_index) in enumerate(skf.split(data, target)):
x_train, x_test, y_train, y_test = data[trn_index], data[te_index], target[trn_index], target[test_index]
clf.fit(x_train, y_train)
clf.score(x_test, y_test)
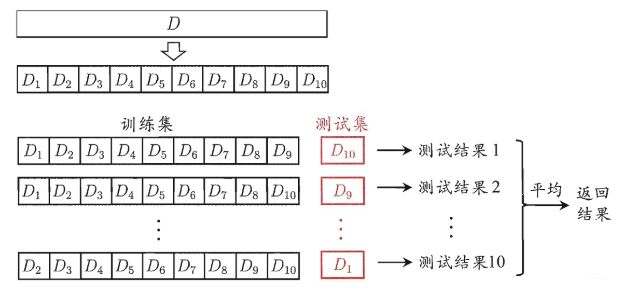
这个代码就是模拟的交叉验证方法, StratifiedKFold分层抽样用于交叉验证, split的时候使用的分层抽样,这样好保持数据分布一致。 看这个代码也了然了, 每次用 k − 1 k-1 k−1个子集的并集作为训练集, 余下的那个作为测试集; 这样可以获得 k k k组训练/测试集,可进行k次训练和测试集, 上面的n_split指定的就是这个 k k k, 最终返回 k k k个测试结果或者求个平均。 这种方法叫做“K折交叉验证”, 看下面图:
与留出法类似, 将数据集D划分为 k k k个子集同样存在多种划分方式,所以为了减少因样本划分不同而引入的差别, k折交叉验证通常随机使用不同的划分重复p次,最终的评估结果是p次k折交叉验证的均值。常见的有“10次10折交叉验证”, 而往往在比赛里面我们常常忽略这一点。
假定数据集 D D D中包含 m m m个样本, 若 k = m k=m k=m的话, 则得到了交叉验证的特例方法: 留一法(LOO).留一法不受随机样本划分方式的影响, 因为 m m m个样本只有唯一的方式划分为 m m m个子集(每个子集包含一个样本)。于是乎,留一法使用的训练集比初始的至少了一个样本,这就使得绝大多数情况下, 留一法评估结果往往认为比较准确。 当然缺陷就是数据集大的时候, 开销较大。 这个方法倒是没用过。
3.3 自助法
上面的两种方法里面有一个问题, 就是保留了一部分样本用于测试, 因此实际评估的模型所使用的训练集其实是比 D D D小的, 带来的问题就是因训练样本规模不同而导致的估计偏差,这个问题我之前没有考虑过。 而留一法中这个偏差的影响倒是小一些,但计算复杂度又太高。
所以自助法是一种减少训练样本规模不同造成的影响又可以高效实验估计的方法,是这么做的:
给定数据集 D D D, 对其进行采样产生数据集 D ′ D' D′: 每次随机从 D D D中选择一个样本, 拷贝到 D ′ D' D′, 再放回去, 再随机选择一个样本,拷贝,放回, 这个过程重复 m m m次, 就能够采出 m m m个样本到 D ′ D' D′, 这时候 D D D和 D ′ D' D′是一样大的。
但这两个不同的是, D D D中的一部分样本会在 D ′ D' D′中多次出现(有放回的抽样), 而有一部分不会出现在 D ′ D' D′中, 这里还做了一个简单估计, 样本在 m m m次采样中始终不会被采到的概率: ( 1 − 1 m ) m \left(1-\frac{1}{m}\right)^{m} (1−m1)m, 这个普通的概率计算了。 这个取极限:
lim m ↦ ∞ ( 1 − 1 m ) m ↦ 1 e ≈ 0.368 \lim _{m \mapsto \infty}\left(1-\frac{1}{m}\right)^{m} \mapsto \frac{1}{e} \approx 0.368 m↦∞lim(1−m1)m↦e1≈0.368
高数上两个重要极限的第二个的推论,不解释。也就是通过自采样, D中有 36.8 % 36.8\% 36.8%的样本没有出现在 D ′ D' D′中。 于是,我们可以将 D ′ D' D′作为训练集, 把没出现在 D ′ D' D′中的那约1/3的数据作为测试集。 这样的测试集叫“包外估计”。这时候,实际评估的模型和期望评估的模型用的都是 m m m个训练样本了。
这个方法在数据集小, 难以有效划分训练/测试集的时候很有用。另外,自助法能从初始数据集中产生多个不同的训练集, 对于集成学习等方法有很大好处。这一点倒是可以作为比赛中的trick。然而,自助法产生数据集改变了初始数据集的分布,会引入估计偏差, 数据量足够的时候, 一般不太常用还是。
3.4 调参与最终模型
大多数学习算法都有参数需要设定,也就是我们所说的超参, 参数配置不同,学得模型的性能往往差别显著, 所以在进行模型评估选择时,除了要对学习算法选择,还需要对算法参数设定,也就是“调参”。 本质上这俩东西没有区别。常用的调参方式, 一般是对每个参数选定范围和变化步长,然后得到具体的模型,然后去评估。
还要注意一点就是选择模型的过程中,我们其实是只用了一部分数据对训练的,另一部分进行的测试,所以并没有用到全量的训练集。 当把模型选择出来了, 参数也调好了,最后交付的时候,我们还需要用全量的数据对其训练, 这个才是我们最终期待的模型呀。这在比赛中往往会有体现,也就是线下测试和线上A榜测试。
想到这里也突然明白了为啥各大比赛里面会有A,B榜的数据了,就像开头说的,测试集也是从现实世界里面抽样出来的数据呀, 仅仅从A榜上表现好的模型,并不一定能说明从另一个测试集上也好。除非A榜的抽样结果能比较好的代表真实世界的数据分布情况。 这也就是kaggle上为啥A榜上排名非常靠前或者拼命拟合A榜数据的人到B榜结果并不太理想的原因。
另外还需要注意一个东西, 就是我们对模型调参的时候,我们所使用的的数据集叫做验证集, 也就是我们需要从训练集中再划分出一部分数据作为验证集,供我们模型调参使用。 于是这时候其实是将整个数据集分成三部分: 训练集,验证集和测试集。
训练集用于训练模型,验证集用于评估模型,测试集进行测试模型。通过训练集,损失函数等已经把模型的参数(权重)控制好了,接下来就是通过验证集,评估指标把模型的超参数定下来(控制变量法的意味)。这个调节过程本质上也是一种学习:在某个参数空间寻找良好的模型配置。 因此,如果基于模型在验证集上的性能来调节模型配置,会很快导致模型在验证集上过拟合(即使没有在验证集上训练模型)。 因为会有信息泄露。 每次基于验证集上的性能来调节模型超参,都会有关于验证数据的信息泄露到模型中。 如果对每个参数只调节一次,泄露的信息很少,验证集仍然可以可靠的评估模型,但是如果重复多次这个过程(运行一次实验,验证集评估,然后修改模型),那么会有越来越多验证集的信息泄露给模型。 最后模型会在验证集上的性能非常好,因为这是不断优化得到的,但是我们真正关心的在全新数据上的性能而不是在验证数据上的新能,因此需要一个模型完全没有见过的数据集评估模型,这就是测试集。测试集模型一定不能够看到, 所以如果基于测试集性能调节模型,泛化能力的衡量会不准确,这也就是为啥要分成3部分的原因了。
好了,下面就是重头戏了。
4. 性能度量
性能度量这个词听起来有点高大上, 其实就是指的衡量模型泛化能力的评价标准, 再说的白话一点就是均方误差,错误率这样的东西。这个东西反映了任务需求,在不同的任务下,使用不同的性能度量,往往导致不同的评判结果,所以判断模型的好坏, 算法,数据和任务需缺一不可。
回归任务中, 常用的就是“均方误差”
E ( f ; D ) = 1 m ∑ i = 1 m ( f ( x i ) − y i ) 2 E(f ; D)=\frac{1}{m} \sum_{i=1}^{m}\left(f\left(\boldsymbol{x}_{i}\right)-y_{i}\right)^{2} E(f;D)=m1i=1∑m(f(xi)−yi)2
这里主要讨论的是分类任务里面的性能度量。
这里约定好符号, 然后好好的看看下面这些概念了, 有些多, 一走神就容易上头,哈哈。
给定样例集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . ( x m , y m ) } D=\{(x_1,y_1),(x_2,y_2), ..(x_m,y_m)\} D={ (x1,y1),(x2,y2),..(xm,ym)}, y i y_i yi是第 i i i个样本的真实label, 要评估学习器 f f f的性能(学习器说白了就是一种函数,反映从输入到输出的映射关系), 就要把学习器的预测结果 f ( x ) f(x) f(x)与真实标记 y y y进行比较。
4.1 错误率和精度
这是分类任务中最常用且简单的两种性能度量,适用于二分类,也适用多分类。
- 错误率: 分类错误的样本数占样本总数的比例
E ( f ; D ) = 1 m ∑ i = 1 m I ( f ( x i ) ≠ y i ) E(f ; D)=\frac{1}{m} \sum_{i=1}^{m} \mathbb{I}\left(f\left(\boldsymbol{x}_{i}\right) \neq y_{i}\right) E(f;D)=m1i=1∑mI(f(xi)=yi)
这公式不用太解释, I ( f ( x i ) ≠ y i ) \mathbb{I}(f(x_i) \neq y_i) I(f(xi)=yi)是一个示性函数, 取值非0即1, 当后面这个条件为真,取值为1, 所以我们求的错误样本个数正好是 f ( x i ) ≠ y i f(x_i) \neq y_i f(xi)=yi的那些样本,这个东西正好把个数统计起来。 这里的 E E E是误差Error的缩写,不是期望。 - 精度: 分类正确的样本数占样本总数的比例
acc ( f ; D ) = 1 m ∑ i = 1 m I ( f ( x i ) = y i ) = 1 − E ( f ; D ) \begin{aligned} \operatorname{acc}(f ; D) &=\frac{1}{m} \sum_{i=1}^{m} \mathbb{I}\left(f\left(\boldsymbol{x}_{i}\right)=y_{i}\right) \\ &=1-E(f ; D) \end{aligned} acc(f;D)=m1i=1∑mI(f(xi)=yi)=1−E(f;D)
这个不解释了, 有了上面,这东西显然。
4.2 查准率,查全率和F1
在数据集不平衡时,上面那俩哥们将不能很好地表示模型的性能。可能会存在准确率很高,而少数类样本全分错的情况,此时应选择其它模型评价指标。
举个例子,对于机场安检中恐怖分子的判断,就不能采用准确率对模型进行评估。我们知道恐怖分子的比例是极低的,因此当我们用准确率做判断时,如果准确率高达 99.999%,就说明这个模型一定好么?
其实正因为现实生活中恐怖分子的比例极低,就算我们不能识别出一个恐怖分子,也会得到非常高的准确率。因为准确率的评判标准是正确分类的样本个数与总样本数之间的比例。因此非恐怖分子的比例会很高,就算我们识别不出来恐怖分子,正确分类的个数占总样本的比例也会很高,也就是准确率高。
实际上, 对于分类不平衡的情况,有两个指标非常重要, 就是精确率和召回率, 也叫查准率和查全率。要想定义这俩东西, 得先来一个混淆矩阵的东西:
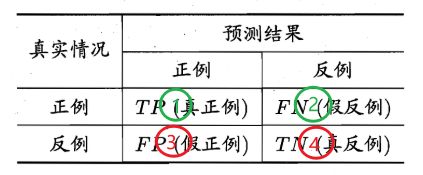
主要看标号, 因为这些字母玩意根本记不住,越记越乱,干脆就直接换成编号。 这①②③④分别代表的对应的样本个数。那么查准率和查全率是啥呢? 我试着用语言描述描述能看出区别不,细品:
- 查准率(precision): 在模型预测为真的样本里面,真实情况中也是真的样本所占的比例, 关注模型预测的准确性,分母就是模型预测为真的样本的总个数,而分子就是模型预测为真且真实情况也为真的样本个数, 即 ① ① + ③ \frac{①}{①+③} ①+③①
- 查全率(recall): 在真实情况为真的样本里面, 模型真正预测为真的样本所占的比例,表示了模型预测的全面性,分母是真实情况为真的样本个数, 分子是真实情况为真模型预测为真的样本个数,即 ① ① + ② \frac{①}{①+②} ①+②①
这俩概念确实有点绕,感觉还是记编号比较好,不要记这TP,FN啥的,这容易记乱套, 并且真实情况用的时候,只要记好这个混淆矩阵,记住这几个编号, 上面这俩指标就非常容易求出来了。因为只要模型定了,阈值定了, 每个编号对应的样本个数就定住了。这里埋个点,如果还是感觉依据公式不会算指标,sklearn给你服务的妥妥的:
from sklearn.metrics import confusion_matrix
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.metrics import f1_score
像上面恐怖分子的例子, 如果此时模型识别不出恐怖分子,那么它的查全率是0, 这样就不会让它在这里滥竽充数了。
下面说一下那个不太好理解的事情,就是查准率和查全率是一对矛盾的度量,一般来说,查准率高时,查全率往往偏低,而查全率高时, 查准率往往偏低。书上有个例子其实挺好理解的,这里也可以再拿上面恐怖分子的例子举一下。
查准率就是我模型预测的恐怖分子里面,是真的恐怖分子所占的比例, 如果想让这个高, 那我模型完全可以把阈值门槛设置的很高,挑最有把握的预测,比如我所有样本按照预测概率从小到大排序,只挑概率最大的前两个,这俩假设真都是恐怖分子。这时候我查准率达到了最大1,但是有可能预测不全,即并没有把恐怖分子都预测出来,查全率低;
而如果我想让查全率高的话, 就是尽可能把恐怖分子都预测出来,那我最极端的情况, 把阈值设置最低, 所有的样本都预测为恐怖分子, 这时候真恐怖分子肯定都预测出来了,查全率达到最大1, 而查准率显然降低了。
如果还是感觉抽象, 那么我们只能上例子了,把上面这个恐怖分子的例子可视化出来了, 灵魂画手出来了
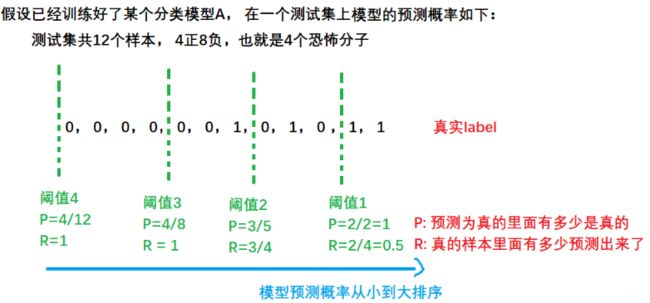
这里按照了预测概率从小到大排的序, 二分类我们都用过, 一般原始输出的sigmoid是直接输出预测概率的, 而最后到底模型预测1还是0往往都是我们根据阈值定的,也就是当概率大于多少的时候,预测为1,否则预测0, 这个多少就是阈值,上面我选了四个阈值,然后在每个阈值下求了一下查准率P和查全率R。至少有两点发现:
- 随着阈值从右往左走,也就是这个门槛慢慢降低的时候, P会慢慢的减小而R会慢慢的增大
- 第二点就是这个R的分母始终没变,P的分母不断变化, 这意味着R与负样本其实没有关系, 而P是受正负样本两类的影响。
通过这样可视化, 应该也能看出为啥往往查准率和查全率是一个矛盾体了。上面埋了个点说模型定了,阈值定了,混淆矩阵就定了, 而这里会发现如果阈值变化的话,其实会对应不同的混淆矩阵,同样会对应不同的查准率和查全率。假设上面图里面,我们从右往左,每过一个样本,就画一条阈值线,算一个P和R的话,到最后,我们是可以得到一个PR曲线的, 也就是查准率随查全率变化曲线如下:
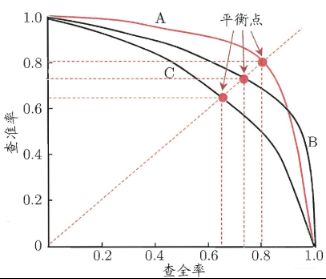
P-R图直观的显示学习器在样本总体上的查全率和查准率。 进行比较时, 如果发现一个学习器的P-R曲线完全被另一个包住, 那么肯定后者优于前者呀,毕竟都包住意味着查准率和查全率都好,又准又全。而如果发生交叉呢? 比如上面的A和B, 这时候如果要比较高低,可以计算各自下面的面积, 但不太好计算,而又想比较A和B怎么办呢? 这时候就用到了综合考虑权衡的指标F1值了。这时候要注意, 目前讨论的都是模型预测为真和真实情况真的情况比较, 还没有考虑反例的情况,后面的roc曲线才一般的用于这种情况下的评估, P-R曲线貌似用的也很少,因为有局限性,下面在roc的时候分析, 下面先看看F1值如何权衡PR的,后面再研究roc这哥们。
F1是基于查准率和查全率的调和平均, 公式如下:
1 F 1 = 1 2 ⋅ ( 1 P + 1 R ) \frac{1}{F 1}=\frac{1}{2} \cdot\left(\frac{1}{P}+\frac{1}{R}\right) F11=21⋅(P1+R1)
看这个公式感觉比较好理解, 调和平均更重视较小值, 如果结合上面P和R的编号公式的话, 这里其实取了倒数使得分母保持了一致, 可以更好的相加了,在一些应用中, 对查准率和查全率的重视程度有所不同, 比如商品推荐系统中, 为了尽可能少打扰用户, 希望推荐内容更准, 而恐怖分子检测中, 希望查的更全,所以往往使用调和平均:
1 F β = 1 1 + β 2 ⋅ ( 1 P + β 2 R ) \frac{1}{F_{\beta}}=\frac{1}{1+\beta^{2}} \cdot\left(\frac{1}{P}+\frac{\beta^{2}}{R}\right) Fβ1=1+β21⋅(P1+Rβ2)
还是感觉这个式子比较清晰一些, 这时候如果 β > 1 \beta>1 β>1, 对查全率有更大影响, 小于1对查准率更大影响。
还有种情况是多次训练和测试的时候(二分类任务), 或者是将一个多分类转成了多个二分类,往往会得到多个混淆矩阵, 这时候如果估算全局性能, 就需要从多个混淆矩阵综合考察查准率和查全率。
两种思路: 一种是先在各个混淆矩阵分别计算P和R, 然后计算平均值, 然后再计算F1, 这叫宏系列:
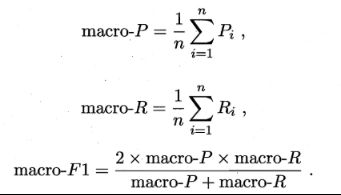
还有种微系列, 就是先将各个混淆矩阵对应元素平均, 得到一个平均系列的混淆矩阵, 然后取出对应的P和R:

目前还没有用到过,先大体了解到这里。 下面来个重头戏了:
4.3 ROC与AUC
这个绝对是比较重要的内容了,AUC在面试中都非常喜欢考, 这里先抛一个问题热热身,假设对于m个样本, 我模型根据预测的概率从小到大排序了,如下图, 这时候, AUC等于几?

脑瓜子瞬间嗡嗡了, AUC,不是一个面积嘛, 怎么成了这样子算AUC? 哈哈, 说明咱对AUC理解的还是不够呀, 下面一起来看看这俩哥们吧。
这两种情况都是一种测试集, 不同阈值下的情况, 上面说过, 不同的阈值选择往往会使得模型的泛化结果不同, 那么就可以根据具体任务需求来合理的调整阈值, 如果更重视查准率, 那么阈值就调的高一点, 如果更重视查全率,就调的低一点。 那这时候, 随着阈值的变化,我们就能得到不同的混淆矩阵。
那么对于模型来讲, 我不同的阈值会有不同的泛化能力, 那这时候,如果想比较两个模型的泛化能力, 这个阈值的高低也会受到影响呀, 这时候,我们就希望能够综合考虑着所有阈值下的模型的泛化性能,这样还可以使得模型适应与不同的任务, 那这时候应该怎么评估模型呢? ROC曲线是常用的工具。
这个曲线其实和PR曲线类似,只不过两个坐标轴不是查准率和查全率了,而是计算真正例率(TPR)和假正例率(FPR), 这俩东西也是借助混淆矩阵计算。这里记录一下子ROC曲线与PR曲线的区别, 来自《百面机器学习》
相比PR曲线,ROC曲线有个特点就是,当正负样本的分布发生变化时, ROC曲线的形状能够基本保持不变, 而P-R曲线的形状一般会发生剧烈的变化, 这个特点让ROC曲线能够尽量降低不同测试集带来的干扰, 更加客观的衡量模型本身的性能。
很多实际问题中, 正负样本的数量往往不均衡,比如计算广告中,正样本往往是负样本的1/10000, 若选择不同的测试集,P-R曲线的变化就会非常大, 而ROC曲线则能够更加稳定的反映模型的好坏,这也是为啥ROC曲线应用广泛的原因。
当然, 选择PR曲线还是ROC曲线还是应该因实际问题而定, 如果希望更多的看到模型在特定数据集上的表现, PR曲线则能够更加直观的反映性能。
这里分析一下ROC曲线为啥能够更加稳定,顺便模拟一下为啥上面两个指标成正比例的关系:
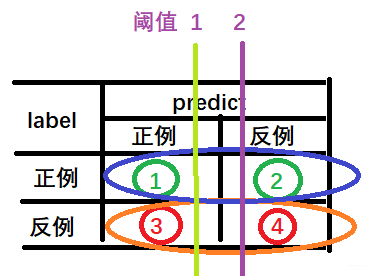
- 真正例率TPR: 这个就是查全率, 真实情况为正的样本中,模型预测为正的比例,公式 ① ① + ② \frac{①}{①+②} ①+②①
- 负正例率FPR: 这个就是真实情况为负的样本中,模型预测为正的比例, 公式 ③ ③ + ④ \frac{③}{③+④} ③+④③
上面分析查全率的时候就说过,这个东西的分母是不变的, 同样的, 下面这个分母也不变, 都是真实情况的正负样本个数。那变的就是分子了(而PR曲线里面的P是受到正反例样本同时的影响的), 看上面这两条阈值, 无论这个阈值从绿色到蓝色还是从蓝色到绿色, 这个①和③都是同步的增加或者减小, 而分母不变, 这也就是为啥ROC曲线是一个正比例曲线的原因,只不过增加或者减少的幅度不一样。下面也是拿上面恐怖分子的例子画一下就了然了:
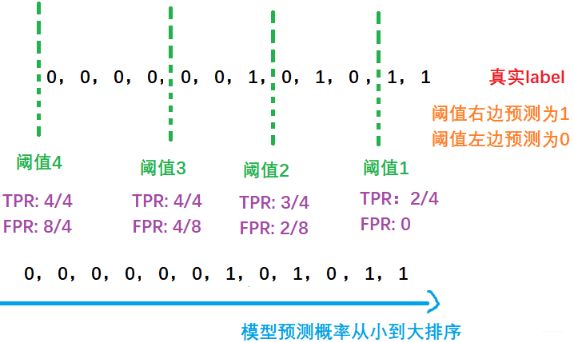
和上面PR类似, 假设我们从右边开始, 每过一个样本画一条阈值线, 计算一个TPR和FPR, 这样过完了所有样本,就会得到ROC曲线了:
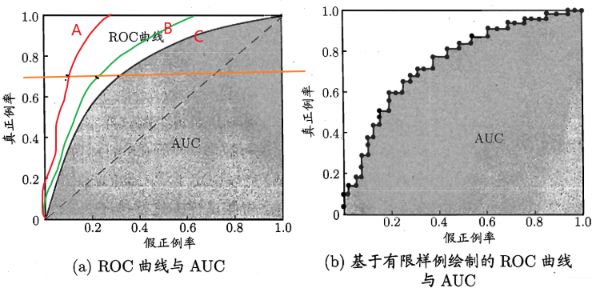
我们上面那个例子画出来是右边这种,左边这种是假设所有样本下的理想值。我们知道ROC曲线越靠近左上方, 表示模型的性能越好,为啥? 看ABC三条线, 性能是A>B>C。 原因是当我们固定住真正例率的时候, 会发现A的假正例率最小或者说,随着真正例率早增加,A假正例率增长最缓慢, 而假正例率是啥? 模型预测为真,实际上人家是假,也就是模型预测错了, 我们当然希望这个增长越缓慢越好了。另一个问题,就是书中解释的右边这个图的画法

这个绘图方式拿上面那个例子一看就非常清楚了:
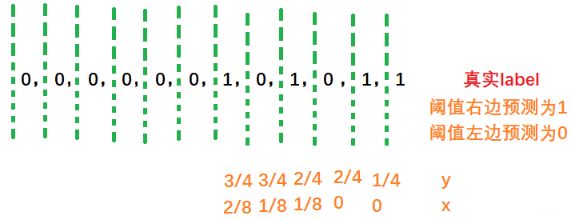
而AUC代表的是下面阴影的面积,显然,这个也是越大越好。 那么AUC真实代表的啥东西呢? AUC表示模型预测样本为正样本的概率大于模型预测样本为负样本的概率的概率值。 AUC越大, 表示模型预测样本为正样本的概率比模型预测样本为负样本的概率大, 书上说的样本预测排序质量的度量,与排序误差有紧密关系,借着来个这样的公式计算 l r a n k l_{rank} lrank, 这个东西一开始没弄明白啥意思,后来整明白了,纸老虎:
ℓ rank = 1 m + m − ∑ x + ∈ D + ∑ x − ∈ D − ( I ( f ( x + ) < f ( x − ) ) + 1 2 I ( f ( x + ) = f ( x − ) ) ) \ell_{\text {rank }}=\frac{1}{m^{+} m^{-}} \sum_{\boldsymbol{x}^{+} \in D^{+}} \sum_{\boldsymbol{x}^{-} \in D^{-}}\left(\mathbb{I}\left(f\left(\boldsymbol{x}^{+}\right)
这个东西代表的是排序损失, 假设模型预测概率从小到大已经排好序,实际上看的就是如果是正样本,理应模型的预测概率要尽量大,也就是尽量的正样本排在负样本前面,这样说明模型预测的准确, 但如果发现正样本前面有负样本了,这时候会产生损失,如果它前面有1个负样本,就产生1的损失, 有两个就产生2, 依次类推, 于是乎公式表示就 I ( f ( x + ) < f ( x − ) ) \mathbb{I}\left(f\left(\boldsymbol{x}^{+}\right)
如果实在不理解也不要紧,会算才是王道, 通过上面的例子,会发现计算非常简单,先上图:
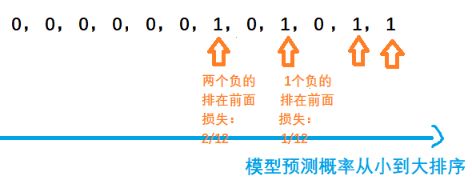
上面这个 l r a n k = 3 / 32 l_{rank}=3/32 lrank=3/32,上图里面的分母有点小错误,公式里面是正样本的个数乘以负样本的个数,也就是 4 × 8 = 32 4\times 8=32 4×8=32, 一开始那个 m + m^+ m+看成个加号了。 注意下。 换成伪代码描述可能会更简单, 从左往右遍历,如果发现正例了,那么就看看他前面有多少个负例, 进行累加,最后除
summ = 0
m1 = 8 # 样本个数
m2 = 4
for i in range(len(nums)):
# 遇到正例了
if nums[i] == 1:
# 看他前面有多少负的
summ += nums[i+1:].count(0)
l_rank = summ / (m1*m2)
而AUC的计算就是:
A U C = 1 − ℓ r a n k \mathrm{AUC}=1-\ell_{\mathrm{rank}} AUC=1−ℓrank
这时候计算得到 A U C = 29 / 32 AUC=29/32 AUC=29/32。 当然根据这个排序关系,也可以直接计算AUC, 那就是从右往左遍历,如果遇到正例, 就看他左边有多少个负例, 然后进行累加:
for i in range(len(nums)-1, -1, -1):
if nums[i] == 1:
summ += nums[:i].count(0)
auc = summ / (m1*m2)
这时候计算就是 ( 8 + 8 + 7 + 6 ) / 32 (8+8+7+6) /32 (8+8+7+6)/32。这就是之前的那个面试题目了。
下面再根据南瓜书上的对35页的这个公式进行解释,也就是AUC的那个面积是怎么算的:
A U C = 1 2 ∑ i = 1 m − 1 ( x i + 1 − x i ) ⋅ ( y i + y i + 1 ) \mathrm{AUC}=\frac{1}{2} \sum_{i=1}^{m-1}\left(x_{i+1}-x_{i}\right) \cdot\left(y_{i}+y_{i+1}\right) AUC=21i=1∑m−1(xi+1−xi)⋅(yi+yi+1)
拿下面的例子概括:
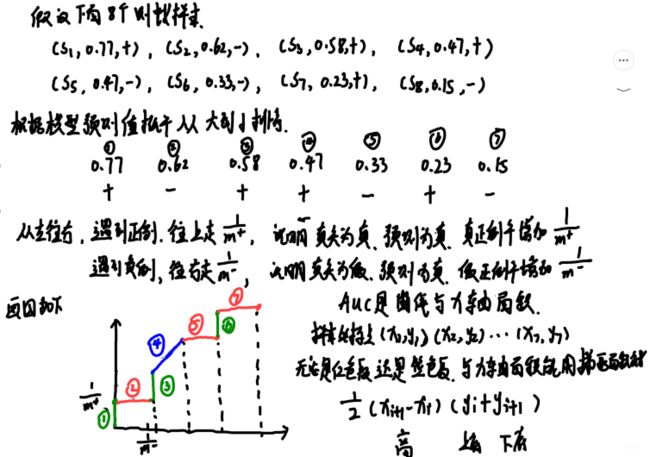
这样,对于所有红色和蓝色围成的面积加和,就是AUC了。而 l r a n k l_{rank} lrank值,在几何上看,其实是上面那个曲线与 y y y轴的面积。 南瓜书的第5也也对这个进行了化简和相关解释,感兴趣的看南瓜书吧, 这里不写了,有点复杂,也是计算梯形的面积,是绿色线和蓝色线与y轴围成面积的计算。
下面再说代价敏感错误率与代价曲线。
4.4 代价敏感错误率与代价曲线
现实任务中会遇到这样的情况: 不同类型的错误所造成的后果不同。 就像上面说的医疗诊断, 本来是健康人预测成病人和本来是病人预测成健康人,这俩的代价是不一样的。 故这种权衡不同类型错误的不同损失, 可为错误加个“非均等代价”。
这样, 代价矩阵就变成了下面这个样子:
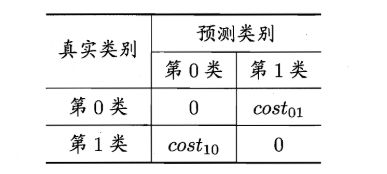
一般情况下 c o s t 01 cost_{01} cost01和 c o s t 10 cost_{10} cost10是不一样的,就是模型判断错误的这两种代价不一样。这里就看出不同了, 之前的那些性能度量隐式的假设了均等代价, 而这里考虑了不同错误造成的不同后果。 我们依然是希望最小化“总体代价”, 那么这个总体代价直观上怎么算呢? 这里需要画个图分析一下子了, 这里书上写的可能迷迷糊糊,不知道在干啥, 这里查了一些资料,才大体上明白了一点, 我们一点点的来推:
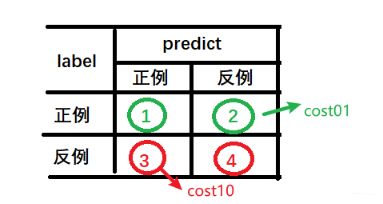
首先先把混淆矩阵拿出来, 上面说希望最小化“总体代价”, 那么这个代价到底怎么表示呢? 其实比较简单,就是
② ① + ② × c o s t 01 + ③ ③ + ④ × c o s t 10 \frac{②}{①+②} \times cost_{01} + \frac{③}{③+④} \times cost_{10} ①+②②×cost01+③+④③×cost10
上式应该比较好理解, 就是犯两类错误的概率乘以相应的代价。 但是我们知道正例和反例的出现也是有一定概率的,也就是上面这两个错误的出现还得基于一定的概率。毕竟②号错误的发生必须先基于正例的出现, ③号错误的发生基于反例的出现。假设某训练集有 m m m个样本, 其中 m + m^+ m+个正样本, m − m^- m−个负样本, 那么正样本出现的概率 p = m + m p=\frac{m^+}{m} p=mm+, 负样本出现的概率就是 1 − p 1-p 1−p, 于是乎我们就得到了“总体代价”的初步形式:
c o s t = p × ② ① + ② × c o s t 01 + ( 1 − p ) × ③ ③ + ④ × c o s t 10 cost=p\times \frac{②}{①+②} \times cost_{01} + (1-p)\times \frac{③}{③+④} \times cost_{10} cost=p×①+②②×cost01+(1−p)×③+④③×cost10
我们的目标就是最小化这个东西。 这里的 p p p表示的某个训练集中正样本的比例。 那这里就先看看这俩带标号的东西是啥, ③ ③ + ④ \frac{③}{③+④} ③+④③这个东西就是前面的 F P R FPR FPR, 也就是假正例率, 而 ② ① + ② \frac{②}{①+②} ①+②②这个东西叫做假反例率FNR,等于 1 − T P R 1-TPR 1−TPR, 这个东西显然了吧。所以上面的式子化简一下:
c o s t = p × F N R × c o s t 01 + ( 1 − p ) × F P R × c o s t 10 cost= p\times FNR \times cost_{01} + (1-p)\times FPR\times cost_{10} cost=p×FNR×cost01+(1−p)×FPR×cost10
那么这时候, 有意思的事情发生了, 在ROC的时候, 我们发现对于某个模型, 如果测试集确定了,那么模型在不同阈值下会对应不同的 ( T P R , F P R ) (TPR, FPR) (TPR,FPR), 这时候如果确定了某个阈值,就能够计算出一组 ( F N R , F P R ) (FNR, FPR) (FNR,FPR), 而这个东西会对应着一个cost值。 所以也就是如果测试集确定了的话,即p确定,此时,如果阈值再确定,就能够得到一个唯一的cost。 那如果再换一个测试集呢, 换p,在同一阈值下,模型会得到另外一个cost, 这样随着换不同的测试集,就会出现很多个cost点,把这些点连起来了, 就组成了一条非归一化的代价曲线。如果切换不同的阈值, 就会得到不同的代价曲线, 所以这个图应该就清楚含义了:
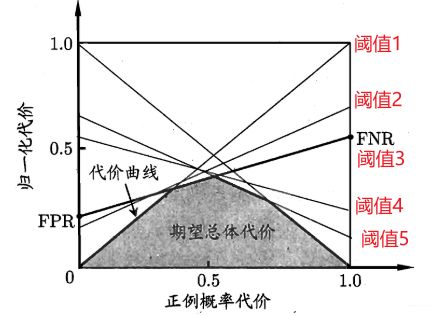
只不过我们这里的代价没有归一化, 横轴目前用的是p,不是p_cost,纵轴用的是cost。 但至少这个应该能明白含义了,那这个东西到底干嘛用呢? 帮助我们在测试集确定的情况下选择模型合适的阈值。 比如某个测试集固定了(p固定), 这时候,对于某个模型应该怎么确定阈值呢? 那就是选择cost最低的那个点的阈值(上图中竖着切一刀肯定有个最低cost)。 有了阈值之后, 模型的各种指标才能算呀。这样就能在这种非均等代价的情况下评估模型了。
这个其实就是代价曲线在做的事情, 书上这个地方说的迷迷糊糊的,不知道在干啥,这是听了一个B站小姐姐的分析之后才get到的。那么接下来就是那几个细节了, 第一个横轴用的自变量不是 p p p, 而是一个叫做正例概率代价的东西:
P ( + ) cos t = p × cost 01 p × cost 01 + ( 1 − p ) × cos t 10 P(+) \cos t=\frac{p \times \operatorname{cost}_{01}}{p \times \operatorname{cost}_{01}+(1-p) \times \cos t_{10}} P(+)cost=p×cost01+(1−p)×cost10p×cost01
下面是个归一化操作,目前先不用管, 上面这个东西当做横轴的自变量,为啥?原因是为了让cost和横轴是线性关系, 而不是非线性, 下面这个图是p和p_cost分别横纵的cost曲线图:
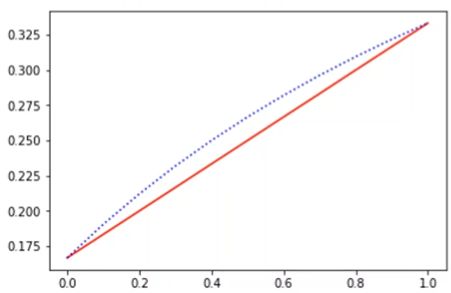
红线这个是p_cost做横轴, 而虚线那个是p做横轴的时候。 线性关系有利于更好的判断, 且这两个就相差一个系数, c o s t 01 cost_{01} cost01是个确定的数。
第二个细节,归一化操作,假设我们不归一化, 那么会发现, 当p=1的时候, c o s t = c o s t 01 × F N R cost = cost_{01} \times FNR cost=cost01×FNR, 但p=0的时候, c o s t = c o s t 10 F P R cost = cost_{10}FPR cost=cost10FPR, 这时候如果 c o s t 10 cost_{10} cost10和 c o s t 01 cost_{01} cost01相差非常大的时候, 画出来的曲线由于量纲的不同,会呈现这样的形状:
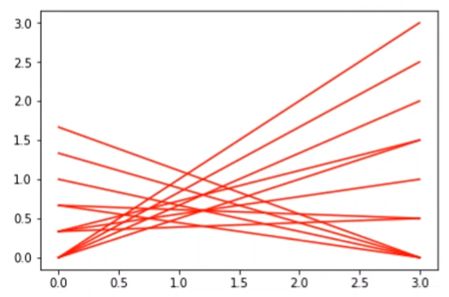
这时候最左边对应的 c o s t 10 cost_{10} cost10的量纲, 右边对应的 c o s t 01 cost_{01} cost01的量纲, 横轴是 c o s t 01 cost_{01} cost01的量纲, 量纲都没有统一起来,这时候图像会倾斜的厉害, 如果我们把量纲进行统一, 也就是横走和纵轴都除以一个 p × cost 01 + ( 1 − p ) × cos t 10 p \times \operatorname{cost}_{01}+(1-p) \times \cos t_{10} p×cost01+(1−p)×cost10, 这时候就变成了下面这种图像:
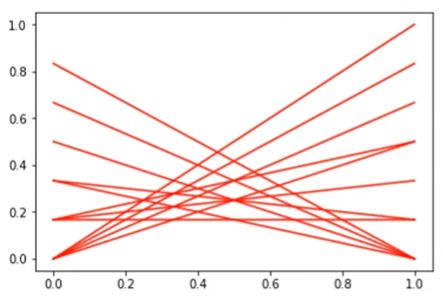
这个具体的程序代码可以去参考上面b站小姐姐的视频, 这里本来想走一遍代码的, 发现实在没时间了,光这东西就写了一天的时间, 耗不起呀实在是。这地方感觉懂原理就行了。 于是乎就得到了书上的 c o s t n o r m cost_{norm} costnorm:
cost n o r m = F N R × p × cos t 01 + F P R × ( 1 − p ) × cost 10 p × cos t 01 + ( 1 − p ) × cos t 10 \operatorname{cost}_{n o r m}=\frac{\mathrm{FNR} \times p \times \cos t_{01}+\mathrm{FPR} \times(1-p) \times \operatorname{cost}_{10}}{p \times \cos t_{01}+(1-p) \times \cos t_{10}} costnorm=p×cost01+(1−p)×cost10FNR×p×cost01+FPR×(1−p)×cost10
代价曲线这个东西差不多理清楚了, 还有个叫做“代价敏感”错误率的, 这里看下公式:
E ( f ; D ; c o s t ) = 1 m ( ∑ x i ∈ D + I ( f ( x i ) ≠ y i ) × cost 01 + ∑ x i ∈ D − I ( f ( x i ) ≠ y i ) × cost 10 ) \begin{aligned} E(f ; D ; c o s t)=& \frac{1}{m}\left(\sum_{\boldsymbol{x}_{i} \in D^{+}} \mathbb{I}\left(f\left(\boldsymbol{x}_{i}\right) \neq y_{i}\right) \times \operatorname{cost}_{01}\right. &\left.+\sum_{\boldsymbol{x}_{i} \in D^{-}} \mathbb{I}\left(f\left(\boldsymbol{x}_{i}\right) \neq y_{i}\right) \times \operatorname{cost}_{10}\right) \end{aligned} E(f;D;cost)=m1(xi∈D+∑I(f(xi)=yi)×cost01+xi∈D−∑I(f(xi)=yi)×cost10)
这个东西到这里应该是挺清楚了, 预测错误的样本个数乘以相应的代价权重,然后求个平均。
5. 比较检验
上面我们做评估,都是基于某个测试集上, 去评估各个模型的性能, 可是这个东西真的准吗?假设我们测出了一个模型在给定测试集的错误率是 ϵ ^ \hat{\epsilon} ϵ^, 我们有多大把握保证模型在我们真实世界里面的数据错误率 ϵ \epsilon ϵ呢? 可别忘了,这个测试集也是采样出来的, 这个测试集上的性能可不一定能代表真实数据的泛化性能,而后者才是我们想要的。 换一个测试集,说不定测试性能又不一样了。那么这时候又面临的一个问题, 我们如何评估模型在真实世界数据中的泛化性能呢?
这里就需要统计假设检验了, 这时候才发现, 研一学习应用数理统计的重要性, 只可惜,忘得妥妥的了, 不过既然学过了,这里多多少少还是能知道在说啥的。
这里做假设检验的思想是这样的, 先假设模型在真实世界中有个泛化错误率 ϵ \epsilon ϵ, 这个也就是学习器在真实数据里面一个样本犯错的概率。 而模型在给定的测试集上的错误率假设是 ϵ ^ \hat{\epsilon} ϵ^,这个我们是能算出来的, 这个也就意味着模型在测试集样本中有 ϵ ^ × m \hat{\epsilon} \times m ϵ^×m个样本误分类了。这时候,其实如果我们知道了真实世界中泛化错误率之后, 我们是能求出从分类错误数为1到 ϵ ^ × m \hat{\epsilon} \times m ϵ^×m个样本的概率的, 因为二分类中,假设的数据是二项分布, 那么概率分布为:
P ( X = k ) = C m k ϵ k ( 1 − ϵ ) m − k , k = 0 , 1 , 2 , … , ϵ ^ × m P(X=k)=C_{m}^{k} \epsilon^{k}(1-\epsilon)^{m-k}, k=0,1,2, \ldots, \hat{\epsilon} \times m P(X=k)=Cmkϵk(1−ϵ)m−k,k=0,1,2,…,ϵ^×m
根据这个公式, 我们从 k = 0 , 1 , 2 , … , ϵ ^ × m k=0,1,2, \ldots, \hat{\epsilon} \times m k=0,1,2,…,ϵ^×m分别计算上面的概率, 就会得到这样的一个图像, 这里假设了 m = 10 , ϵ = 0.3 m=10, \epsilon=0.3 m=10,ϵ=0.3:
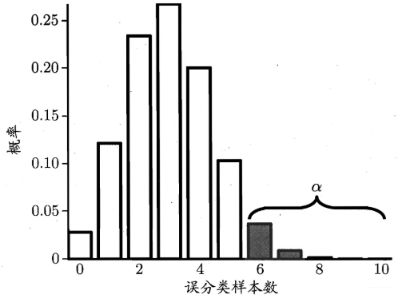
这时候, 我们可以使用“二项检验”来对 ϵ ⩽ 0.3 \epsilon \leqslant 0.3 ϵ⩽0.3的假设进行检验,在 1 − α 1-\alpha 1−α概率内所能观测到的最大错误率:
ϵ ˉ = max ϵ s.t. ∑ i = ϵ 0 × m + 1 m ( m i ) ϵ i ( 1 − ϵ ) m − i < α \bar{\epsilon}=\max \epsilon \quad \text { s.t. } \quad \sum_{i=\epsilon_{0} \times m+1}^{m}\left(\begin{array}{c} m \\ i \end{array}\right) \epsilon^{i}(1-\epsilon)^{m-i}<\alpha ϵˉ=maxϵ s.t. i=ϵ0×m+1∑m(mi)ϵi(1−ϵ)m−i<α
这里的 1 − α 1-\alpha 1−α反映了结论的置信度。此时,若测试错误率 ϵ ^ \hat{\epsilon} ϵ^小于临界值 ϵ ˉ \bar{\epsilon} ϵˉ, 则可根据二项检验得出结论: α \alpha α的显著程度下, 接收零假设,即 ϵ ⩽ 0.3 \epsilon \leqslant 0.3 ϵ⩽0.3, 这样就能得到了真实世界中泛化误差范围。
在很多时候, 我们会进行多次训练/测试, 得到多个测试错误率, 这时候就可以利用"t检验"去判断真实数据的泛化误差。 具体操作是先提出假设 μ = ϵ 0 \mu=\epsilon_{0} μ=ϵ0, 然后构造检验统计量去进行验证。 这里可以构造t分布, 双边检验的思想。 具体的看书吧, 这里确实需要先补一波应用数理统计的思想才可以, 但思想没变。
后面还有多个测试集两个算法的检验方法交叉验证t检验, 一个测试集两种算法的McNemar检验,多个测试集多种算法的Friedman检验和Nemenyi后续检验, 具体用到的时候再说吧, 太难了, 没大看明白这里, 且讲真,不知道咋用, 所以先不看, 等以后用到的时候再回来补充。
6. 方差与偏差
上面我们通过实验估计出了模型的泛化性能, 也通过假设验证了这种泛化性能, 但模型为什么会出现这样的泛化性能呢? 这里把学习器的期望泛化错误率进行拆解。 算法在不同训练集上的结果很可能不同, 那这时候通过不同的测试集训练, 就会得到学习算法的期望预测:
f ˉ ( x ) = E D [ f ( x ; D ) ] \bar{f}(\boldsymbol{x})=\mathbb{E}_{D}[f(\boldsymbol{x} ; D)] fˉ(x)=ED[f(x;D)]
那么就能算的,使用样本数相同的不同训练集产生的方差为
var ( x ) = E D [ ( f ( x ; D ) − f ˉ ( x ) ) 2 ] \operatorname{var}(\boldsymbol{x})=\mathbb{E}_{D}\left[(f(\boldsymbol{x} ; D)-\bar{f}(\boldsymbol{x}))^{2}\right] var(x)=ED[(f(x;D)−fˉ(x))2]
噪声为
ε 2 = E D [ ( y D − y ) 2 ] \varepsilon^{2}=\mathbb{E}_{D}\left[\left(y_{D}-y\right)^{2}\right] ε2=ED[(yD−y)2]
期望输出与真实标记的差别称为偏差, 即公式表示
bias 2 ( x ) = ( f ˉ ( x ) − y ) 2 \operatorname{bias}^{2}(\boldsymbol{x})=(\bar{f}(\boldsymbol{x})-y)^{2} bias2(x)=(fˉ(x)−y)2
于是就是对期望泛化误差进行了分解, 具体的看书(南瓜书对西瓜书的公式作了更详细的推导), 最后的结论很重要:
E ( f ; D ) = bias 2 ( x ) + var ( x ) + ε 2 E(f ; D)=\operatorname{bias}^{2}(\boldsymbol{x})+\operatorname{var}(\boldsymbol{x})+\varepsilon^{2} E(f;D)=bias2(x)+var(x)+ε2
即泛化误差可以分解为偏差,方差和噪声之和。
- 偏差度量了学习算法的期望预测与真实结果的偏离程度,刻画学习算法本身的拟合能力
- 方差度量同样大小的训练集的变动所导致的学习性能的变化,刻画数据扰动所造成的的影响
- 噪声表达了当前任务上任何学习算法所能达到的期望泛化误差的下界,即刻画了学习问题本身的难度
这个分解式说明泛化性能是由学习算法的拟合能力, 数据的充分性以及学习任务本身难度共同决定, 给定学习任务, 为了取得良好的泛化性能,既需要模型充分拟合数据(偏差小), 也需要使得数据的扰动产生的影响小(方差小)。
一般来说, 偏差和方差是有冲突的, 给定学习任务,假设我们能控制学习算法的训练程度, 则在训练不足的时候, 学习器的拟合能力不够强,训练数据的扰动不足以使得学习器发生显著变化,此时偏差主导泛化错误率;
随着训练程度的加深, 学习器的拟合能力逐渐增强, 训练数据发生的扰动渐渐能被学习器学习到, 方差主导了泛化错误率;
训练充足之后, 学习器的拟合能力非常强, 训练数据发生轻微扰动都会导致学习器发生显著变化, 若训练数据自身的,非全局特性被学习到了, 就会发生过拟合。
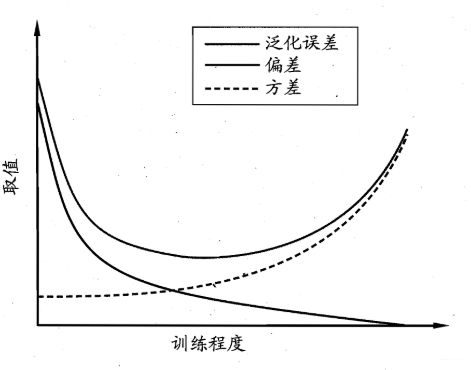
这个过拟合发生的过程我详细记录了一下,因为这个地方我之前的理解有误区, 总弄不太清楚偏差,方差和欠拟合,过拟合的关系,现在真正体会到了高偏差欠拟合和高方差过拟合的真正含义。也知道了原来模型的泛化性能是与偏差和方差同时有关系的, 需要两者都小, 之前谈到模型的泛化能力差,总以为是模型过拟合导致的方差大, 而并没有悟到后面的方差占主导。
7. 小总
这篇文章的梳理用了一天的时间, 不过感觉还是挺有价值的, 第二章讲的这些东西其实之前很多都用过, 可就是不知道原因, 还有一些是很重要且一直容易混了的东西, 这次通过梳理逻辑, 画图又进行理解, 对模型的性能度量方法,以及之间的关系有了更加深刻的体会, 对方差偏差的理解也有了新的体会, 还学习到了数据集划分的一种自助方法,说不定以后用到集成的时候真可以试一波哈哈。 第二章就到这里了,知识点还是很多很杂的, 但这些东西都是非常底层,原理的东西,学习完了之后,感觉踏实多了哈哈。 后面西瓜书就是各种具体的机器学习算法了, 这次要放慢速度, 慢慢去品味每个算法。 Rush!
参考:
- 周志华 - 《机器学习》
- 谢文睿 - 《机器学习公式详解》