拓展 欧几里得算法 求逆元_ECC椭圆曲线加密算法：有限域和离散对数

Hi all，我来翻译第二篇啦。若大家发现那些翻译的不够准确还望指出，不胜感激。首先放上原文链接：

http://andrea.corbellini.name/2015/05/23/elliptic-curve-cryptography-finite-fields-and-discrete-logarithms/​andrea.corbellini.name

在上一篇文章里，我们已经展示了在实数域上的椭圆曲线在“群”上是如何使用的。尤其是，我们还针对“加”(point addition) 定义了一个规则：对于在一条线上的三个点，他们的和是0（P+Q+R=0）. 我们也推出了一个几何方法和代数方法去计算这些点的加法。

然后呢，我们介绍了标量积(scalar multiplication) （nP=P+P+...+P），我们还发现了一个“简单的”算法去计算这些标量积。double and add

整数域模p

首先，有限域是一个带有有限元素的集合。比如，有一个有限域是整数模p的集合（integers mod p,p是素数），可表示为

或

,我们一般用后者。

在这个有限域中，我们有两个二元操作：加（+）和乘( * )。这两种操作都是封闭的，满足结合律和交换律，[这块的封闭应当这样理解：在有限域中，两个数的加和乘的结果仍然在这个有限域中。--译者注] 且含有一个独一无二的单位元，对于所有的有限域里的元素，都有一个独一无二的相反数。最后，乘法还满足分配律：

。

整数模p的集合包含所有从0到

的整数。加法和乘法都按模数运算规则去计算。这里有一些

的例子：

• 加：
• 减：
• 乘：
• 加法逆元：
  的确：
• 乘法逆元：
  的确：

如果这些式子你觉得不太能理解，那么你可能需要一些关于模运算的入门指导，请参考：Khan Academy.

就如我前面提到的，整数模p是一个域，因此上面列的所有属性都是满足的。请注意p是素数这个条件很重要！比如 整数模4的集合就不是域：2没有乘法逆元（

无解）。

模p的除法

我们即将定义在

上的椭圆曲线，但是在这之前我们需要弄清在

上

代表什么？可以简单表示为：

，

等于x 乘上 y的逆元。这个解释给了我们基本的做除法的方法：1.求逆元，2.做乘法。

用欧几里得拓展算法来计算乘法逆元非常的“简单易做”，它的时间复杂度是

(或者是

如果考虑bit长度的话) 在最坏的情况下。 这里不会给出欧几里得拓展算法的细节，但是放上Python的代码：

def 

在

上的椭圆曲线

现在，所有的必要元素都已就位，用来在

上定义椭圆曲线，它的形式是点集，在上一篇文章中我们是这样写的：

现在，可以写成：

这里的0仍然是无限远的点，a和b是

上的两个整数。

图1

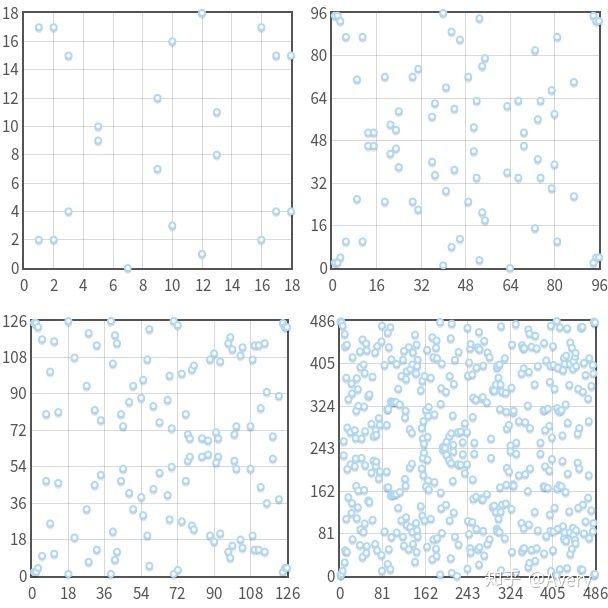
图1：曲线

且

. 请注意，对于每一个

，至多有两个对称的点满足：

.

图2

图2：曲线

是一个奇点，并且在

处有三个点，这是一个无效的椭圆曲线。

图1是连续的椭圆曲线在xy轴平面上表现为不相交的点集。在

上的椭圆曲线仍然可以形成阿贝尔群。（elliptic curves in

still form an abelian group. ）

点加

显然，我们需要改变一点点关于加法的定义，为了使它能更好的工作在

。 在实数域上，我们约定俗成三个对齐的点的和是0（

）。在实数域上这个定义没有问题，就是共线。但是在

上，我们如何定义三个点的对齐？

我们可以说，如果一条直线连接了三个点，这三个点就是对齐的。当然，

上的直线不同于

上的直线。也就是说，

上的直线就是点集(

)，这个点集满足

(这是带有"

"的标准的线性方程式)

请见注释1（方程式在这里长的不标准...）

注释1: 上图的所有点都在

，

请注意连接某些点的一次方程

在图中不停的“重复（因为有mod 127...）”自己。

鉴于这已经是一个群，所以点加具备一些通用的属性:

• (单位元的定义)
• 给定一个非零点Q, 逆元-Q和它具有相同的横坐标，但是纵坐标相反。或者还有一种方式，
  。举个例子，如果曲线在
  上有一个点
  ，逆元是
  。
• （相反数的定义）

代数和

点加的计算和上篇文章中基本差不多，除了要在每个等式后加上“

”。因此，鉴于

和

，我们可以计算

，如下：

如果

，假设斜率是：

如果

，斜率是：

这个式子长的和在实数域的点加差不多吧，这不是个巧合，事实上，以上的方程式适用于任一域，无论是有限域还是无限域（除了

和

）。有个问题是：证明这些法则通常要引入一些复杂的数学概念。但是我发现Stefan Friedl给出的证明浅显易懂。如果你对“为什么这个方程式几乎适用于所有环境”很感兴趣，read it!

言归正传，由于在几何方法上有一些问题，所以我们不会定义一个几何方法。比如，在第一篇稿子中，我们说 要计算

我们需要在曲线

上正切，但是如果不是一条线的话（without continuity, 即没有连续性），“正切”没有任何意义。确实我们可以权衡利弊后做一些变通，但是这种纯几何方法太复杂而且不实用。

椭圆曲线的阶

我们之前说到每个在有限域上的椭圆曲线都由有限个点组成。那么我们不禁要问：到底是多少个点？

首先，我们要定义一下 在一个群有多少个点就叫做这个群的“阶”（order）【在此放上wiki关于order的解释】。

群举从

到

所有可能的值去数有多少个点不太可行，因为它的时间复杂度是

，当

很大的时候，这算下来就很慢很慢。

还好，有一个更快的算法来计算阶：Schoof算法。在此不展细节，我们只需要知道他的复杂度是多项式时间(大名鼎鼎的Polynomial-Time.在此奉上wiki)

数乘和循环子群

在实数域乘法的定义是：

我们可以用倍加算法（请见上一篇）去做乘法，时间复杂度是

（或者

，这里的

是

的二进制倍数）。

在

上的椭圆曲线的乘法有个很有意思的属性。取一个曲线：

和点

，现在来计算P的所有倍数：

p=(3,6)的所有倍乘的取值只有5个点(0, P, 2P, 3P, 4P )然后不停的循环重复。我们能很容易的发现椭圆曲线上的数乘和模运算的加法非常相似。

• ...

到此，我们发现了两个事情：第一，P的倍乘只有5个取值，永远不会出现第6个。第二，他们是循环重复的。我们可以写成这样： （

取任意整数）

所以呢，这五个式子可以被“压缩”成一个（模运算）：

。

不仅如此，我们可以立即验证：P的加法是个闭环。（These five points are closed under addition. ）这意味着：不论我加的是0, P, 2P, 3P 还是 4P， 结果永远都是这五个点中的一个。Again, 其他点永远不会出现在这根椭圆曲线的结果里。

这个规则同样适用于所有的点，不仅仅是对

。事实上，对于任意的

:

这意味着：如果我们将n倍的P进行相加，我们获得的仍然是P的倍数(If we add two multiples of P, we obtain a multiple of P)【由于这个定理太重要了，我把英文也放上来】。（比如，nP的相加是个闭环。）这足够来证明：nP的集合是椭圆曲线形成的群里的一个具有循环性质的子群（the set of the multiples of P is a cyclic subgroup of the group formed by the elliptic curve.）。这里的点

叫做循环子群的 生成器 或者 基点。

子群的阶

我们可以扪心自问下，由P生成子群的阶到底是什么？（或者，P的阶是什么？）为了回答这个问题，我们不能使用Schoolf的算法，因为这个算法只能在整个的椭圆曲线上生效，在子群上无效。在解决这个问题之前，我们需要打点地基：

• 到现在为止，我们已经定义了：阶，就是一个群的点的数量。这个定义仍然是有效的，但是在循环的子群里我们可以下一个新的，与前面的定义相等的定义：
  的阶是最小的正整数
  ，
  满足的条件是
  。事实上，我们回顾前面的例子，
  。
• 的阶和椭圆曲线是有联系的，拉格朗日定理告诉我们，子群的阶是父群的阶的因子。换句话说，如果一个椭圆曲线包含
  个点，它的一个子群包含
  个点，那么
  是
  的因子。

以上两条规则结合起来给我们指了一条明路，如何根据基点

找到子群的阶：

1. 使用Schoof的算法去计算椭圆曲线的阶
   。
2. 找到
   所有的因子。
3. 对于
   的每一个因子
   ,计算
   。
4. 找到最小的且满足
   的
   ,
   就是子群的阶。

举个栗子，在

上的曲线

的阶是

。它的子群的阶可能是

。如果我们代入曲线上的点

我们可以发现

。因此，

的阶是7。

请注意，很重要的一点是一定一定要是最小的因子，而不是随机的一个因子。如果我们随机处理一下，我们可能取

，但它不是子群的阶，仅仅是一个倍数。

另一个例子：定义在

椭圆曲线上的方程式

的阶是

，这是一个素数，所以它的子群的阶可能只含有1和37. 很容易我们就可以猜出来，当

的时候，子群仅包含一个点，就是0（参考上篇文章的point at infinity）。当

时，子群包含椭圆曲线的所有的点。

找基点

在ECC算法中，我们想找到一个阶数比较大的子群。所以通常呢，我们会选择一条椭圆曲线，然后去计算它的阶（

）, 选择一个以较大的因子作为子群的阶（

），最终，依此找到一个合适的基点。也就是说，我们不会选择一个基点然后去计算它的阶，我们会反着来操作一波。

首先，我们要介绍一个术语。拉格朗日定理说，

里的

永远是一个整数（因为

是

的因子）。这里的

有个名字：辅因子（cofactor of the subgroup）。

现在，思考一下对于椭圆曲线中的每一个点，我们有

，且

是任意一个

的倍数。借助辅因子的概念，我们可以写成：

。

假设

是素数，这个方程式告诉我们：点

生成了一个阶为

的子群（除了当

，在这个例子中子群的阶是1）。

现在我们总结一下算法：

1. 计算椭圆曲线的阶
   。
2. 选择一个阶为
   的子群。n必须是素数且必须是
   的因子。【至于为什么一定是素数，请见下一篇文章】
3. 计算辅因子
   。
4. 在曲线上选择一个随机的点
   。
5. 计算
   。
6. 如果
   是0，那么回到步骤4。否则我们就已经找到了阶为
   和辅因子是
   的子群的生成器/基点。

请注意，上面这个算法仅仅适用于

是素数的情况下。如果

不是素数，那么

的阶可以是

的任何一个因子。

离散对数

当有一条连续的椭圆曲线，我们现在要讨论的问题是：如果我们已知

，要想得到

，我们应该怎么去计算这个

?

这个问题，就是椭圆曲线中大名鼎鼎的离散对数问题，它被认为是个很难很难的问题！【插一句，这也是ECC的核心的核心，也是为什么ECC安全的原因】。到目前为止，没有找到一个能在多项式时间内解出来的算法。因此，也没有数学证明。

这个难题同样也是其他涉及离散对数问题的加密算法的难题，比如DSA算法，D-H密钥交换算法，ElGamal算法。不同点在于，上述算法使用了模幂算法而不是数乘。模幂算法的离散对数问题可以简述为：当我们知道

，

，那么如何求

?

这两个问题中，值都是“离散”的，因为他们都取自于有限的集合（循环的子群）。而且都是“对数”，就是普通意义上的对数运算。

ECC有趣的地方在于，到今天为止，它的离散问题看上去比其他密码学中的离散问题难多了。这就说明我们可以用更少的位数的整数

做到和其他加密算法一样安全级别的加密效果。

其他

下一篇会介绍：键值对的生成，ECDH和ECDSA算法。

【我已经尽量的还原文章了，其中加了一点点个人见解和wiki的简介。阅读愉快:)--xiaopei】