无标题文章

Lab 1 Homework 1.4 1.5

Based on the knowledge of discrete system properties, we analyzed several systems and proved our predictions with MATLAB.

1.4(a) The system y[n] = sin((π/2)x[n]) is not linear. Use the signals x1[n] =δ[n] and x2[n] = 2δ[n] to demonstrate how the system violates linearity.

MATLAB code

 %1.4 problem (a）
n = [-3 : 3];
x1 = [0 0 0 1 0 0 0];
% let x1 be an unit impulse signal
x2 = 2*x1;
% use x2 to testify the system
y1 = sin((pi/2)*x1);
y2 = sin((pi/2)*x2);

% plot x1 x2 y1 and y2
subplot(4,1,1);
stem(n,x1)
title('x1[n]');

subplot(4,1,2);
stem(n,y1)
title('y1[n]');

subplot(4,1,3);
stem(n,x2)
title('x2[n]');

subplot(4,1,4);
stem(n,y2)
title('y2[n]');

Result

1.4a.png

Observe the second and the forth image. If the system is linear, then for x2[n] = 2x1[n], y2[n] should be 2y1[n], however, the result doesn't match the assumption.

1.4(b) The system y[n] = x[n] + x[n+1] is not causal. Use x[n] = u[n] to demonstrate this.

MATLAB code

% 1.4 problem(b)
n1 = [-5:9];
x = [zeros(1,5) ones(1,10)];
subplot(3,1,1);
stem(n1,x)
title('x[n]')
x1 = [zeros(1,4) ones(1,11)];
subplot(3,1,2);
stem(n1,x1) 
title('x[n+1]')
y = [x] + [x1];
subplot(3,1,3);
stem(n1,y)
title('y[n]')

Result

1.4b.png

For example, for y[-1]=x[-1]+x[0], the system requires future data x[0], so it is not causal.

1.4(c) Prove the system y[n] = log(x[n]) is not stable

MATLAB code

%1.4 problem(c)
n = [0:50];
x = 2*sin(n);
y = log(x);
subplot(2,1,1);
stem(n,x)
subplot(2,1,2);
stem(n,y)

Result

1.4c.png

The upper one is x[n] = sin[n] which is a bounded signal, while the lower one is the output of this signal by the system, we can tell the output is not bounded. So the system is not stable.

1.4(d) Prove the system in part (a) is not invertible.

MATLAB code

%1.4 problem(d)
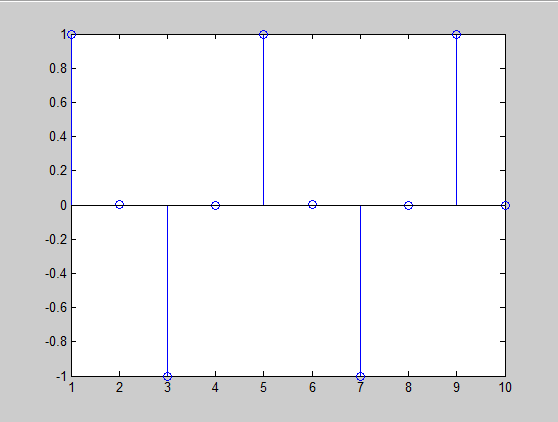
n = [1:10];
x = [1 2 3 4 5 6 7 8 9 0];
y = sin((pi/2)*x);
stem(n,y)

Result

1.4d.png

When the input n includes 2 4 6 ... and 2k, the system gives the same output: zero. So the system is not inversible.

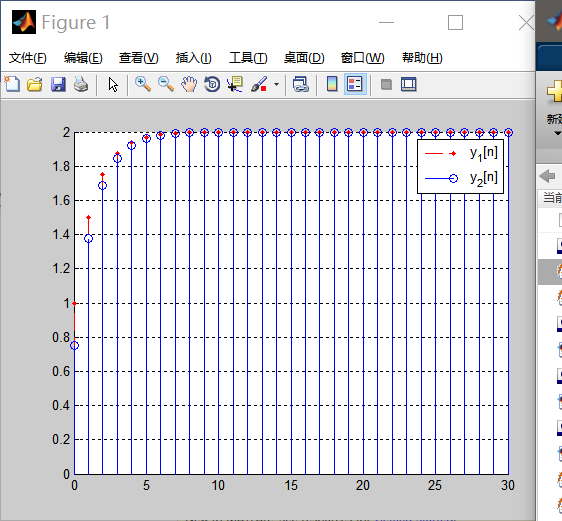
1.4(e) Analyze y[n] = x^3[n] and state whether it is linear, time invariant, causal, stable and invertible.

The conclusion

for y[n] = x^3[n] , it is not linear, but is time invariant, causal, stable and invertible.

MATLAB code

n = [-2 : 2];
x1 = [-1 0 1 0 1]; x2 = 2*x1;
y1 = x1.^3; y2 = x2.^3;
subplot(4,1,1); stem(n,x1)
title('x1[n]');
subplot(4,1,2); stem(n,y1)
title('y1[n]');
subplot(4,1,3); stem(n,x2)
title('x2[n]');
subplot(4,1,4); stem(n,y2)
title('y2[n]');