常用涡识别方法的Tecplot实现（Q准则、λ2 准则、delta准则、Omega准则）

惯例声明：本人没有相关的工程应用经验，只是纯粹对相关算法感兴趣才写此博客。所以如果有错误，欢迎在评论区指正，不胜感激。本文主要关注于算法的实现，对于实际应用等问题本人没有任何经验，所以也不再涉及。

本来想写一个拉格朗日结构LSC的文章，但是不知道是算法理解有问题还是计算参数设置问题，自己搞的结果总是神似形不似，所以放弃，改写一个偏实际应用方面的。

0 前言

0.1 欧拉法涡识别

欧拉法涡识别基于函数与场论的思想，对流场的信息进行计算加工，得到描述涡的函数。之后对涡函数取截面或等值面等方法，展示涡的结构。

大多数欧拉法涡识别都具有平移不变性，即涡识别结果不会因为场的平移而变化。
但是大多数欧拉法涡识别都不具备旋转不变性，即涡识别结果会因为坐标系定义的方向变化而变化（尤其是旋转坐标系下的涡识别）。

常用的涡识别方法有涡量法、Q方法、λ2方法（Lambda-2）、Δ方法（Delta）、λci方法（Lambda-ci)、Ω方法(Omega）。具体的原理不再细说，本文只介绍最终结果。

本文的参考文献以及术语定义来源为：
[1]第三代涡识别方法及其应用综述（王义乾, 桂南）2019
[2]A review of methods for vortex identification in hydroturbines（张宇宁）2018
[3]Tecplot官方Github：https://github.com/Tecplot/handyscripts/tree/master/macro

0.2 Tecplot中的涡识别

Tecplot在新版本中陆续添加了很多新的涡识别方法，以Q准则为例。

第一步，点击Analyze中的Calculate Variables

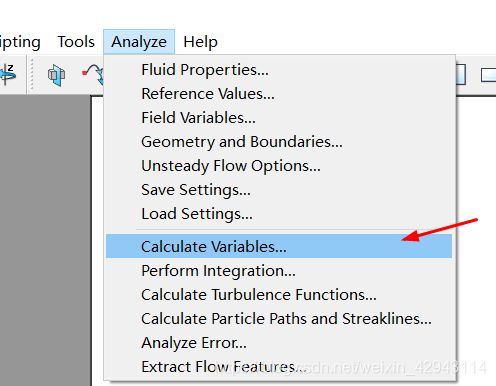
第二步，点击Select，选择Q Criterion，选择Ok。然后点击Calculate计算即可。

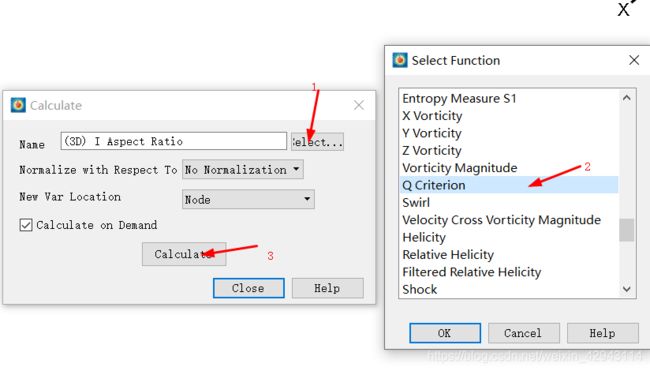
如果由于Tecplot的版本太低，或者想要计算的涡识别方法没有被Tecplot收录，就需要自己计算编辑计算了。当然，优先用Tecplot自带的函数计算，那些函数计算经过优化更省时间。
那么可以采取下面的方法：
第一步，点击Data里的Alter，选择Specify Equations

第二步：输入公式，点击Compute计算（这里用到的公式在后面会给出，不用抄）

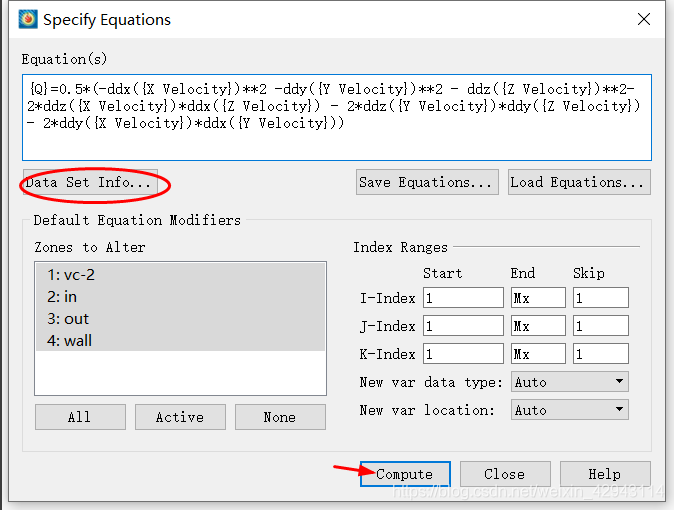
这里注意Tecplot的公式格式：
1 次方用的不是^，而是**
2 变量用花括号{}括起来，具体变量名称参考Data Set Info里面，不同软件不同设置得到的变量名称往往不一样。（也可以用V3来的形式，来表示第3个变量，变量顺序同样参考Data Set Info）

1 涡量法

涡量法是描述涡最简单的方法，但是难以区分旋转导致的涡与剪切导致的涡（比如会把边界层识别出来）。而且难以识别虽然涡量较小但是结构清晰的涡。

Tecplot内Analyze中的Calculate Variables中，自带函数Vorticity Magnitude计算涡量。
由于内置函数计算速度远大于自己编辑的公式，所以不再给出函数。

2 Q方法

这个是最经典的方法，计算量小，而且结果也很不错，推荐使用。

一般选择Q>0的某个等值面作为涡。

Tecplot内Analyze中的Calculate Variables中，自带函数Q Criterion
由于内置函数计算速度远大于自己编辑的公式，所以尽可能用Tecplot内的函数。

公式为
$$Q=0.5\ast (\Vert B{\Vert }_F^2-\Vert A{\Vert }_F^2)$$
其中，$\Vert B{\Vert }_F^2$表示矩阵B的范数的平方，等同于矩阵B所有元素的平方和。
而矩阵A和矩阵B分别为速度梯度的对称张量和反对称张量，即：
$$A=0.5\ast (\Delta V+\Delta V^T)$$
$$B=0.5\ast (\Delta V-\Delta V^T)$$
其中T代表矩阵的转置。速度张量的定义如下：
$$\Delta V=\left(\begin{array}{ccc}\text{Ux}& \text{Uy}& \text{Uz}\\ \text{Vx}& \text{Vy}& \text{Vz}\\ \text{Wx}& \text{Wy}& \text{Wz}\end{array}\right)$$

2.1 2D的Tecplot公式

{Ux}=ddx({X Velocity})
{Uy}=ddy({X Velocity})
{Vx}=ddx({Y Velocity})
{Vy}=ddy({Y Velocity})
{Q}=0.5*(-{Ux}**2 -{Vy}**2-2*{Uy}*{Vx})

2.2 3D的Tecplot公式

{Ux}=ddx({X Velocity})
{Uy}=ddy({X Velocity})
{Uz}=ddz({X Velocity})
{Vx}=ddx({Y Velocity})
{Vy}=ddy({Y Velocity})
{Vz}=ddz({Y Velocity})
{Wx}=ddx({Z Velocity})
{Wy}=ddy({Z Velocity})
{Wz}=ddz({Z Velocity})
{Q}=0.5*(-{Ux}**2 -{Vy}**2 - {Wz}**2- 2*{Uz}*{Wx} - 2*{Vz}*{Wy} - 2*{Uy}*{Vx})

3 λ2方法

该方法是利用当地的压强最低点来判定涡的位置，因为涡核处压强比较小。经过输运方程的无粘不可压假设推导，可以得到λ2方法的计算公式。

相比较Q方法，λ2方法的公式比较复杂。首先需要计算A^2+B^2，然后再计算其特征根，按照大小排序选择第2个特征值，作为涡的判据。这里λ2方法中的λ2就是指的是这个特征值。

这里参考博客：流体中相干涡结构在tecplot中的可视化-Q判据及λ2判据

一般选择λ2<0的某个等值面作为涡。

其中，A^2+B^2的公式可以化简为

$$\begin{gathered} A^2+B^2= \\ \left(\begin{array}{ccc}U{x}^2+UyVx+UzWx& \frac{1}{2}\left(\left(Ux+Vy\right)\left(Uy+Vx\right)+VzWx+UzWy\right)& \frac{1}{2}\left(UyVz+\left(Ux+Wz\right)\left(Uz+Wx\right)+VxWy\right)\\ \frac{1}{2}\left(\left(Ux+Vy\right)\left(Uy+Vx\right)+VzWx+UzWy\right)& V{y}^2+UyVx+VzWy& \frac{1}{2}\left(UzVx+UyWx+\left(Vy+Wz\right)\left(Vz+Wy\right)\right)\\ \frac{1}{2}\left(UyVz+\left(Ux+Wz\right)\left(Uz+Wx\right)+VxWy\right)& \frac{1}{2}\left(UzVx+UyWx+\left(Vy+Wz\right)\left(Vz+Wy\right)\right)& W{z}^2+UzWx+VzWy\end{array}\right) \end{gathered}$$
转换为Tecplot语法：

{Ux}=ddx({X Velocity})
{Uy}=ddy({X Velocity})
{Uz}=ddz({X Velocity})
{Vx}=ddx({Y Velocity})
{Vy}=ddy({Y Velocity})
{Vz}=ddz({Y Velocity})
{Wx}=ddx({Z Velocity})
{Wy}=ddy({Z Velocity})
{Wz}=ddz({Z Velocity})
{T11}={Ux}**2+{Uy}*{Vx}+{Uz}*{Wx}
{T12}=0.5*(({Ux}+{Vy})*({Uy}+{Vx})+{Vz}*{Wx}+{Uz}*{Wy})
{T13}=0.5*(({Uz}+{Wx})*({Ux}+{Wz})+{Uy}*{Vz}+{Vx}*{Wy})
{T22}={Uy}*{Vx}+{Vy}**2+{Vz}*{Wy}
{T23}=0.5*(({Vy}+{Wz})*({Vz}+{Wy})+{Uy}*{Wx}+{Uz}*{Vx})
{T33}={Uz}*{Wx}+{Vz}*{Wy}+{Wz}**2

这里还需要计算特征根，然而Tecplot内没有相应的函数，只能利用Tool工具栏下的Tensor Eigensystem进行计算。

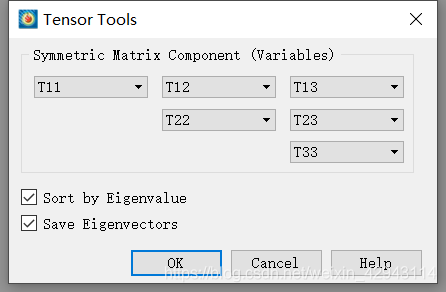
在Tensor Eigensystem里，按照顺序选择刚才计算的矩阵各个元素，点击Ok计算。此时Tecplot会自动生成一大堆和特征值相关的变量。当然别的特征值我们不关心，我们只关心λ2。

之后在绘图界面中，选择EgnVal2变量，进行等值面的绘图。

4 Δ方法

Q判据为涡的地方，Δ方法也会判定为涡。但Q判据不是涡的地方，有可能根据Δ方法也会判定为涡。

一般选取Δ>0的某个值的等值面，作为涡的展示。

这里参考的是Tecplot官网给出的计算
https://kb.tecplot.com/2019/05/02/calculate-delta-criterion/

{Ux}=ddx({X Velocity})
{Uy}=ddy({X Velocity})
{Uz}=ddz({X Velocity})
{Vx}=ddx({Y Velocity})
{Vy}=ddy({Y Velocity})
{Vz}=ddz({Y Velocity})
{Wx}=ddx({Z Velocity})
{Wy}=ddy({Z Velocity})
{Wz}=ddz({Z Velocity})
{P} = -({Ux}+{Vy}+{Wz})
{Q} = (-{Uy}*{Vx}-{Uz}*{Wx}-{Vz}*{Wy}+{Ux}*{Vy}+{Wz}*{Ux}+{Wz}*{Vy})
{R} = ({Ux}*({Vz}*{Wy}-{Vy}*{Wz})+{Uy}*({Vx}*{Wz}-{Wx}*{Vz})+{Uz}*({Wx}*{Vy}-{Vx}*{Wy}))
{R2} = ({R}+(2/27)*{P}**3-{Q}*{P}/3)
{Q2} = ({Q}-{P}**2/3)'
{Delta} = ({Q2}/3)**3+({R2}/2)**2

5 λci方法

λci方法是在Δ方法的基础上进行计算得到的。
原理是当Δ>0时，速度梯度张量存在2个复数特征根，其特征根的虚部就是λci。

一般选取λci>0的某个值的等值面，作为涡的展示。

具体的计算方法本人能力有限，没有看懂。
这里参考的是Tecplot官网给出的计算（同上面的Δ方法）
https://kb.tecplot.com/2019/05/02/calculate-delta-criterion/

{Ux}=ddx({X Velocity})
{Uy}=ddy({X Velocity})
{Uz}=ddz({X Velocity})
{Vx}=ddx({Y Velocity})
{Vy}=ddy({Y Velocity})
{Vz}=ddz({Y Velocity})
{Wx}=ddx({Z Velocity})
{Wy}=ddy({Z Velocity})
{Wz}=ddz({Z Velocity})
{P} = -({Ux}+{Vy}+{Wz})
{Q} = (-{Uy}*{Vx}-{Uz}*{Wx}-{Vz}*{Wy}+{Ux}*{Vy}+{Wz}*{Ux}+{Wz}*{Vy})
{R} = ({Ux}*({Vz}*{Wy}-{Vy}*{Wz})+{Uy}*({Vx}*{Wz}-{Wx}*{Vz})+{Uz}*({Wx}*{Vy}-{Vx}*{Wy}))
{R2} = ({R}+(2/27)*{P}**3-{Q}*{P}/3)
{Q2} = ({Q}-{P}**2/3)'
{Delta} = ({Q2}/3)**3+({R2}/2)**2
{Beta2} = IF ({Delta}>=0 ,(ABS(SQRT(ABS({Delta}))-{R2}/2))**(1/3),0)
{Beta3} = IF ({Delta}>=0 ,(ABS(SQRT(ABS({Delta}))+{R2}/2))**(1/3),0)
{LambdaCi}=(SQRT(3)/2)*({Beta2}+{Beta3})

6 Ω方法

Ω方法被认为是最新一代涡识别方法。

其具有归一化阈值的特点，不像前面的各种方法需要调试不同的阈值，Ω方法的阈值被归一化到了0-1之间。
而且Ω方法被认为可以同时展示强涡核弱涡。

一般参考文献里推荐取Ω=0.52作为等值面来展示涡。

Ω方法和Q方法公式类似：

$$\Omega =\frac{\Vert B{\Vert }_F^2}{\Vert A{\Vert }_F^2+\Vert B{\Vert }_F^2+ϵ}$$
其中小量$ϵ$目的是防止零除以零的现象出现，它理论上只要是大于零的某个量就行。参考文献里给出了推荐值，为：
$$ϵ=1/1000\ast max(\Vert B{\Vert }_F^2-\Vert A{\Vert }_F^2)$$
结合上面Q准则的公式，可以知道大约等于500分之一的最大的Q准则计算值。
$$ϵ=max(Q)/500$$
当然要想知道最大的Q准则计算值需要先计算一遍Q准则（感觉有点奇怪）。实际应该没有那么严格，大约是那个量级附近的数就行了。

6.1 2D的Tecplot公式

{Ux}=ddx({X Velocity})
{Uy}=ddy({X Velocity})
{Vx}=ddx({Y Velocity})
{Vy}=ddy({Y Velocity})
{A2}={Ux}**2+0.5*({Uy}+{Vx})**2+{Vy}**2
{B2}=0.5*({Uy}-{Vx})**2
{Omega}={B2}/({A2}+{B2}+1/500*替换成最大Q值)

6.2 3D的Tecplot公式

{Ux}=ddx({X Velocity})
{Uy}=ddy({X Velocity})
{Uz}=ddz({X Velocity})
{Vx}=ddx({Y Velocity})
{Vy}=ddy({Y Velocity})
{Vz}=ddz({Y Velocity})
{Wx}=ddx({Z Velocity})
{Wy}=ddy({Z Velocity})
{Wz}=ddz({Z Velocity})
{A2}={Ux}**2+0.5*({Uy}+{Vx})**2+{Vy}**2+0.5*({Uz}+{Wx})**2+0.5*({Vz}+{Wy})**2+{Wz}**2
{B2}=0.5*(({Uy}-{Vx})**2+({Uz}-{Wx})**2+({Vz}-{Wy})**2)
{Omega}={B2}/({A2}+{B2}+1/500*替换成最大Q值)

7 不同方法对比

这里我用Fluent简单计算了一个射流流场，网格量比较少，比较丑。但是大概比较不同涡识别方法，大概够用了，也具有足够多的涡结构。


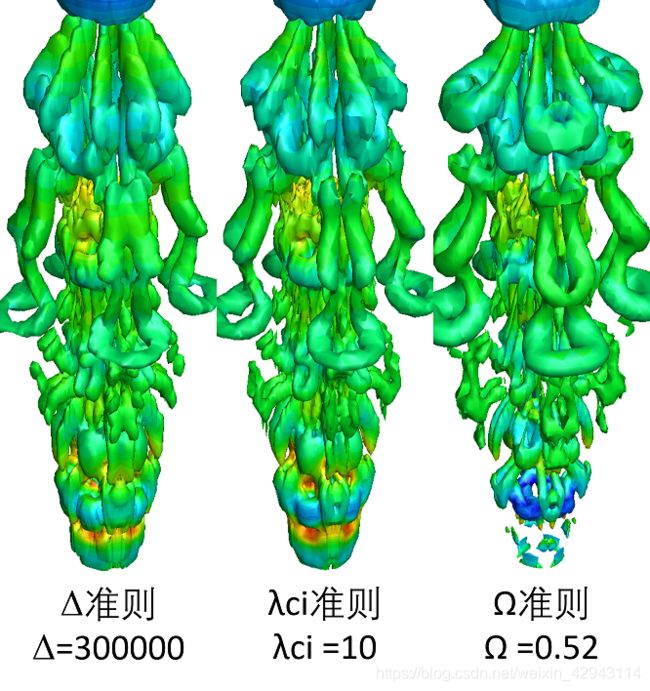
可以看到其实各种涡识别方法其实大同小异，调一下参数大多长得也比较像。

个人感觉，平时默认用Q准则就足够了，其余算法计算量大，但是和Q比起来没有特别明显的优势。

不过Ω准则识别出的马蹄涡基本没有断的，而且阈值无脑选文献中推荐的0.52也不需要做过多修改，比较方便。可以说是这里面效果最好的。