0.简介
不稳定的四个排序算法
选择排序: 0(n2)
希尔排序: 0(n1.3)
快速排序:0(nlog2n)
堆排序:0(nlog2n)
稳定的三个排序算法
插入排序: 0(n2
冒泡排序:0(n2)
归并排序: 0(nlog_2n)
所谓稳定和不稳定:
稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
Note:以下动图均来自网络
1.选择排序:
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置。然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到全部待排序的数据元素排完。
__author__ = '__yuanlei__'
def select():
for i in range(0, len(s) - 1):
index = i
for j in range(i + 1, len(s)):
if s[index] > s[j]:
index = j
s[i], s[index] = s[index], s[i]
# 打出输出结果.
if __name__ == "__main__":
arr = [3,4,5,7,6,8,0,9,1,-1,-4]
output = select(arr)
print output
2.希尔排序
希尔排序的思路就是:
先把待排序的序列分成若干个子序列,并对这若干个子序列分别进行插入排序。这若个子序列的元素间隔是不断减小的,直到间隔为1(此时对序列进行排序就等同于插入排序了)。
__author__ = '__yuanlei__'
def shellsort(arr):
gaps = [5,3,1]
#对于每一个gap都执行一次插入排序
for gap in gaps:
for i in range(gap,len(arr)):
preIndex = i - gap
curr = arr[i]
while preIndex>=0 and arr[preIndex]>curr:
arr[preIndex+gap] = arr[preIndex]
preIndex -= gap
arr[preIndex+gap] = curr
return arr
# 打出输出结果.
if __name__ == "__main__":
arr = [3,4,5,7,6,8,0,9,1,-1,-4]
output = shellsort(arr)
print output
3.快速排序
#快速排序的思想:设置一个基准,对基准左右两边进行分别的排序
__author__ = '__yuanlei__'
def QuickSort(array, left, right):
if left < right:
#第一步定好那个基准
#然后在基准的左边右边用递归的形式使用QuickSort
IndexBaseline = ZoneDivision(array, left, right)
#表示当前Indexbaseline的值就是一个中间值,不用再Sort
#所以下面两个函数的结束和开始为IndexBaseline-1 和 IndexBaseline+1
QuickSort(array, left, IndexBaseline-1)
QuickSort(array, IndexBaseline+1, right)
return array
def ZoneDivision(array, left, right):
baseline = left
index = baseline + 1
for i in range(index, right+1):
if array[i]4.堆排序
堆:程序运行过程中动态分配的内存,比如c中的malloc和c++中的new。这种效率会比较慢,但不用预先定义。
栈:操作系统在建立某个进程或线程时,为其创建的内存空间,该内存空间具有FIFO的特性。当程序结束时,只需要修改栈的头指针就可以直接释放内存了,因此这种效率较快,但需要预先定义。
堆排序的思想:堆是一种数据结构,在这里我们可以将这个堆看成是一种特殊的完全二叉树,该二叉树的特点是其非叶子节点的数必定要大于(或者)小于其子节点上的数。堆排序就是一个构建最大堆或最小堆的过程(本例子只讲建立最大堆),每次构建一个最大堆后,将该最大堆的根节点和最右边的叶子节点进行交换,并脱离堆。然后对剩下的len-1个节点的堆再进行构建最大堆的过程,直到所有的节点都脱离堆之后排序完成。
在模仿堆的数据结构的时候(完全二叉树),对于节点的编码利用最直观的层序遍历。可以利用一维数组实现,这种情况下对于起始索引为0的一维数组来说:
- 父节点i的左孩子索引为2i+1;
- 右孩子索引为2i+1+1;
- 子节点i对应的父节点索引为floor( (i-1)/2 ),表示向下取整。
__author__ = '__yuanlei__'
def build_max_head(arr,heapsize,root_index):
#根据给定的根节点计算左右节点的index
left_index = 2*root_index+1
right_index = left_index+1
max_num_index = root_index
#如果左节点大于根节点,那么max_num_index=left_index
if left_indexarr[max_num_index]:
max_num_index=left_index
#如果右节点大于根节点,那么max_num_index=right_index
if right_indexarr[max_num_index]:
max_num_index=right_index
if max_num_index != root_index:
arr[root_index],arr[max_num_index] = arr[max_num_index],arr[root_index]
#进行下一个节点的build_max
build_max_head(arr,heapsize,max_num_index)
def head_sort(arr):
#从最后一个节点开始,对整个堆(完全二叉树)进行build_max
for i in range((len(arr-1)-1)/2,-1,-1):
build_max_head(arr,len(arr),i)
#对从最后一个节点开始往前遍历
for i in range(len(arr)-1, -1, -1):
#这个时候最大值就在根节点
#所以把这个最大值放到有序队列中
#简单来说就是把最大值放到最后
arr[i],arr[0] = arr[0],arr[i]
#互换之后,堆中就少了一个元素,所以当前堆的个数变了,变为i
#此时由于堆只变了根节点,因此只需要对根节点进行build_max
build_max_head(arr,i,0)
if __name__ == '__main__':
arr = [1,3,5,7,9,2,8,0,-1,-2]
output = merge_sort(arr)
print output
5.插入排序
__author__ = '__yuanlei__'
def InsertSort(arr):
for i in range(1,len(arr)):
preIndex = i -1
current = arr[i]
while (preIndex>=0 and arr[preIndex]> current):
arr[preIndex+1] = arr[preIndex]
preIndex -= 1
#此时preIndex已经被挪到-1了,所以要对第一个元素赋值的话
#就要对preIndex+1进行操作
arr[preIndex+1]=current
return arr
if __name__ == '__main__':
arr = [0,5,3,6,9,7,1,2,8]
output = InsertSort(arr)
print output
6.冒泡排序
__author__ = '__yuanlei__'
def maopaosort(arr):
for i in range(len(arr)):
for j in range(len(arr)-i-1):
if arr[j] > arr[j+1]:
arr[j],arr[j+1]=arr[j+1],a[j]
return arr
if __name__ == '__main__':
input = [2,4,1,3,6,0]
output = maopaosort(input)
print(output)
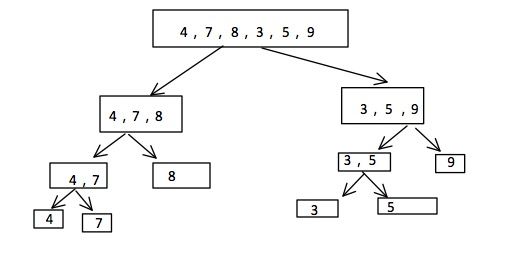
7.归并排序
归并的思路在于先分再和,分的过程如下:
先将数组进行一半一半的拆分,直到不能再拆分未知。
之后进行合并的操作,这个合并的操作主要是合并另个有序数组。我们先比较两个有序数组的第一个元素,将小的放到一个空数组中,然后将这个小的数据原始所在的那个数组的指针往后移一个。继续与另一个数组进行比较,继续将小的放到空数组的下一个中。直到任何一个数组全部的元素出完之后,将另一个数组的所有元素放到空数组接下来的位置。
def merge(left_arr, right_arr);
empty = []
left_index = right_index = 0
#当两个数组都有元素的时候
while left_index < len(left_arr) and right_index < len(right_arr):
if left_arr[left_index] < right_arr[right_index]:
empty.append(left_arr[left_index])
left_index += 1
else:
empty.append(right_arr[right_index])
right_index+= 1
#当left数组的元素归并完了
if left_index == len(left_arr):
for num in right_arr[right_index:]:
empty.append(num)
#当right数组的元素归并完了
else:
for num in left_arr[left_index:]:
empty.append(num)
def merge_sort(arr):
if len(arr)<=1:
return arr
middle_index = len(arr)/2
left_arr = merge_sort(arr[:middle_index])
right_arr = merge_sort(arr[middle_index:])
return merge(left_arr, right_arr)
if __name__ == '__main__':
arr = [1,3,5,7,9,2,8,0,-1,-2]
output = merge_sort(arr)
print output
给自己打个小广告
本人211硕士毕业生,目前从事深度学习,机器学习计算机视觉算法行业,目前正在将我的各类学习笔记发布在我的公众号中,希望感兴趣一起学习的同学们可以关注下~~~
本人微信公众号:yuanCruise