1.1. 数组拷贝(掌握)
需求:定义一个方法arraycopy完成int类型数组的拷贝
1.1.1. 实现int类型数组元素拷贝(掌握)
从指定源数组中从指定的位置开始复制指定数量的元素到目标数组的指定位置。
src - 源数组
srcPos - 源数组中的开始索引位置
dest - 目标数组
destPos - 目标数据中的开始索引位置
length - 要复制元素的数量
代码如下:
package cn.wolfcode.array;
public class ArrayCopyDemo {
public static void main(String[] args) {
int[] a = new int[] { 10, 20, 30, 40, 50, 60, 70 };
int[] b = new int[10];
System.out.println(java.util.Arrays.toString(b));;// 打印拷贝前的数组
ArrayCopyDemo.arraycopy(a, 2, b, 4, 3);
System.out.println(java.util.Arrays.toString(b));;// 打印拷贝后的数组
}
static void arraycopy(int[] src, int srcPos, int[] dest, int destPos, int length)
{
for (int index = 0; index < length; index++) {
dest[destPos + index] = src[srcPos + index];
}
}
}
输出结果:
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 30, 40, 50, 0, 0, 0]
1.1.2. java.lang.System类(会调用)
System类中提供了数组元素拷贝的方法,并且支持任意类型的数组拷贝,而不仅仅是int类型数组。
如果还看不懂,使用鼠标左键点击该方法名称,进入该方法的详细:
操作代码:
package cn.wolfcode.array;
public class ArrayCopyDemo {
public static void main(String[] args) {
int[] a = new int[] { 10, 20, 30, 40, 50, 60, 70 };
int[] b = new int[10];
System.out.println(java.util.Arrays.toString(b));// 打印拷贝前的数组
System.arraycopy(a, 2, b, 4, 3);
System.out.println(java.util.Arrays.toString(b));// 打印拷贝后的数组
}
}
1.2. 排序操作(掌握原理)
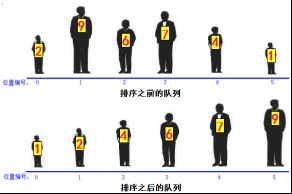
需求:完成对int[] arr = new int[]{2,9,6,7,4,1}数组元素的升序排序操作.
1.2.1. 冒泡排序原理(掌握原理)
对未排序的各元素从头到尾依次比较相邻两个元素的大小关系,如果前一个元素大于后一个元素则交换位置,经过第一轮比较后可以得到最大值,同理第二轮比较后出现第二大值等。
针对int[] arr = new int[]{ 2, 9, 6, 7, 4, 1 }数组元素做排序操作:
该数组有6个元素,只需要5轮比较。
第1轮比较:需要比较5次,比较完出现最大值。
第2轮比较:需要比较4次,比较完出现第二大值。
第3轮比较:需要比较3次,比较完出现第三大值。
...
可以看出如有N个元素,则需要N-1轮比较,第M轮需要N-M次比较。
交换数组中两个元素的方法
static void swap(int[] arr, int index1, int index2) {
int temp = arr[index1];
arr[index1] = arr[index2];
arr[index2] = temp;
}
排序代码:
package cn.wolfcode.array;
public class ArraySortDemo{
public static void main(String[] args) {
int[] arr = new int[] { 2, 9, 6, 7, 4, 1 };
System.out.println(Arrays.toString(arr));//排序前
ArraySortDemo.sort(arr);
System.out.println(Arrays.toString(arr));//排序后
}
static void sort(int[] arr) {
//第一轮:
for (int i = 1; i <= arr.length-1; i++) {
if (arr[i - 1] > arr[i]) {
ArraySortDemo.swap(arr, i - 1, i);
}
}
//第二轮:
for (int i = 1; i <= arr.length - 2; i++) {
if (arr[i - 1] > arr[i]) {
ArraySortDemo.swap(arr, i - 1, i);
}
}
//第三轮:
for (int i = 1; i <= arr.length - 3; i++) {
if (arr[i - 1] > arr[i]) {
ArraySortDemo.swap(arr, i - 1, i);
}
}
}
}
寻找规律,优化上述代码:
static void sort(int[] arr) {
for (int times = 1; times <= arr.length - 1; times++) {
//times表示第几轮比较,值为:1,2,3,4,5
for (int i = 1; i <= arr.length - times; i++) {
if (arr[i - 1] > arr[i]) {
App.swap(arr, i - 1, i);
}
}
}
}
1.2.2. Arrays类中的排序方法(会调用)
Arrays类中已经提高了数组排序的方法sort,并且是调优之后的,性能非常优异,在开发中只需要我们直接调用该方法即可即可。
package cn.wolfcode.array;
public class ArraySortDemo{
public static void main(String[] args) {
int[] arr = new int[] { 2, 9, 6, 7, 4, 1 };
System.out.println(Arrays.toString(arr));//排序前
java.util.Arrays.sort(arr);
System.out.println(Arrays.toString(arr));//排序后
}
}
1.3. 二分法查找(掌握原理)
查找数组元素的算法:
线性查找:从头找到尾,性能比较低。
二分法查找(折半查找):前提数组元素是有序的,性能非常优异。
1.3.1. 二分法搜索原理(掌握原理)
猜数字游戏:
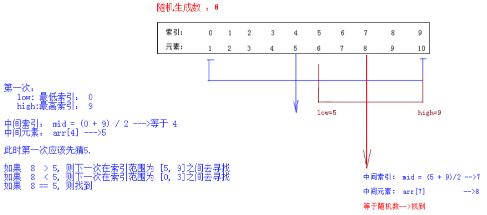
电脑随机生成一个[ 1 , 100 ]之间的整数a,等玩家来猜,猜之后,电脑提示出三种结果:你猜的数偏大,偏小和猜中了。此时为了使用最少次数猜中,玩家必定先猜(1+100)/2的商50,如果此时电脑提示猜的偏小了,那就能推断出该随机数在[ 51 , 100 ]之间,此时再猜(51+100)/2的商75,如果电脑提示猜大了,那么该随机数必在[ 51 , 74 ]之间,那么继续猜(51+74)/2的商,如此每次都可以排除剩下结果一半的可能性,直到猜到为止。
代码如下:
package cn.wolfcode.array;
public class ArraySearchDemo{
public static void main(String[] args) {
int[] arr = new int[] { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
int index = ArraySearchDemo.binarySearch(arr, 8);
System.out.println(index);
}
static int binarySearch(int[] arr, int key) {
int low = 0;
int high = arr.length - 1;
while (low <= high) {
int mid = (low + high) / 2;
int midVal = arr[mid];
if (midVal < key) {
low = mid + 1;
} else if (midVal > key) {
high = mid - 1;
} else {
return mid;
}
}
return -1; // 没有找到
}
}
1.3.2. Arrays类中的二分法查找方法(会调用)
package cn.wolfcode.array;
public class ArraySearchDemo{
public static void main(String[] args) {
int[] arr = new int[] { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
int index = java.util.Arrays.binarySearch(arr, 8);
System.out.println(index);
}
}
小结:排序和二分法查找的原理需要掌握,会调用Arrays类中方法完成相关功能。
若要获得最好的学习效果,需要配合对应教学视频一起学习。需要完整教学视频,请参看https://ke.qq.com/course/272077。