机器学习(六)——XGBoost算法
XDBoost算法
- 1 XGBoost算法原理
-
- 1.1 算法推导
- 1.2 优缺点
1 XGBoost算法原理
XGBoost算法在Gradient Boosting框架下实现,是一个优化的分布式梯度增强库,旨在实现高效,灵活和便携,本质上还是一个GBDT。Xgboost算法以CART决策树为子模型,通过Gradient Tree Boosting实现多棵CART树的集成学习,得到最终模型。 XGBoost提供了并行树提升(也称为GBDT,GBM),可以解决超过数十亿个样例的问题。
1.1 算法推导
这里引用陈天奇的论文进行推导,设我们的数据集为 D = { ( x i , y i ) } ( ∣ D ∣ = n , x i ∈ R m , y i ∈ R ) \mathcal{D}=\left\{\left(\mathbf{x}_{i}, y_{i}\right)\right\}\left(|\mathcal{D}|=n, \mathbf{x}_{i} \in \mathbb{R}^{m}, y_{i} \in \mathbb{R}\right) D={ (xi,yi)}(∣D∣=n,xi∈Rm,yi∈R)
(1)首先我们来构建目标函数:
假设有K棵树,那么第 i i i个样本的最终输出为 y ^ i = ϕ ( x i ) = ∑ k = 1 K f k ( x i ) , f k ∈ F \hat{y}_{i}=\phi\left(\mathrm{x}_{i}\right)=\sum_{k=1}^{K} f_{k}\left(\mathrm{x}_{i}\right), \quad f_{k} \in \mathcal{F} y^i=ϕ(xi)=∑k=1Kfk(xi),fk∈F,其中 F = { f ( x ) = w q ( x ) } ( q : R m → T , w ∈ R T ) \mathcal{F}=\left\{f(\mathbf{x})=w_{q(\mathbf{x})}\right\}\left(q: \mathbb{R}^{m} \rightarrow T, w \in \mathbb{R}^{T}\right) F={ f(x)=wq(x)}(q:Rm→T,w∈RT)。( w q ( x ) w_{q(\mathbf{x})} wq(x)为每个叶子结点的预测值,在后边我们会进一步定义)。
因此,目标函数可构建为: L ( ϕ ) = ∑ i l ( y ^ i , y i ) + ∑ k Ω ( f k ) \mathcal{L}(\phi)=\sum_{i} l\left(\hat{y}_{i}, y_{i}\right)+\sum_{k} \Omega\left(f_{k}\right) L(ϕ)=i∑l(y^i,yi)+k∑Ω(fk)其中 ∑ i l ( y ^ i , y i ) \sum_{i} l\left(\hat{y}_{i}, y_{i}\right) ∑il(y^i,yi)为损失函数, ∑ k Ω ( f k ) \sum_{k} \Omega\left(f_{k}\right) ∑kΩ(fk)为正则化项。
(2)叠加式的训练
由于XGBoost本质上还是一个GBDT,因此我们采用加法模型和前向逐步计算的方式进行训练,但是(1)中的目标函数针对的是模型整体,不只与当前步有关,还有前边已建立的树模型有关,因此还不能进行逐步计算。那么我们能否将其优化到目标函数只与当前步有关呢?
对于给定的样本 x i x_i xi,初始预测值 y ^ i ( 0 ) = 0 \hat{y}_i^{(0)} = 0 y^i(0)=0,向前计算则 y ^ i ( 1 ) = y ^ i ( 0 ) + f 1 ( x i ) \hat{y}_i^{(1)} = \hat{y}_i^{(0)} + f_1(x_i) y^i(1)=y^i(0)+f1(xi), y ^ i ( 2 ) = y ^ i ( 0 ) + f 1 ( x i ) + f 2 ( x i ) = y ^ i ( 1 ) + f 2 ( x i ) \hat{y}_i^{(2)} = \hat{y}_i^{(0)} + f_1(x_i) + f_2(x_i) = \hat{y}_i^{(1)} + f_2(x_i) y^i(2)=y^i(0)+f1(xi)+f2(xi)=y^i(1)+f2(xi),以此类推,最终的结果为 y ^ i ( K ) = y ^ i ( K − 1 ) + f K ( x i ) \hat{y}_i^{(K)} = \hat{y}_i^{(K-1)} + f_K(x_i) y^i(K)=y^i(K−1)+fK(xi)。 y ^ i ( K − 1 ) \hat{y}_i^{(K-1)} y^i(K−1)为前 K − 1 K-1 K−1棵树的预测结果, f K ( x i ) f_K(x_i) fK(xi)为第K棵树的预测结果。由此可见,可以分解为前 K − 1 K-1 K−1步与当前步,因此对目标函数的损失和正则化项进一步分解为: L ( K ) = ∑ i = 1 n l ( y i , y ^ i ( K − 1 ) + f K ( x i ) ) + ∑ k Ω ( f k ) = ∑ i = 1 n l ( y i , y ^ i ( K − 1 ) + f K ( x i ) ) + ∑ k = 1 K − 1 Ω ( f k ) + Ω ( f K ) \mathcal{L}^{(K)}=\sum_{i=1}^{n} l\left(y_{i}, \hat{y}_{i}^{(K-1)}+f_{K}\left(\mathrm{x}_{i}\right)\right)+\sum_{k} \Omega\left(f_{k}\right)\\ =\sum_{i=1}^{n} l\left(y_{i}, \hat{y}_{i}^{(K-1)}+f_{K}\left(\mathrm{x}_{i}\right)\right)+\sum_{k=1} ^{K-1}\Omega\left(f_{k}\right)+\Omega\left(f_{K}\right) L(K)=i=1∑nl(yi,y^i(K−1)+fK(xi))+k∑Ω(fk)=i=1∑nl(yi,y^i(K−1)+fK(xi))+k=1∑K−1Ω(fk)+Ω(fK)
由于进行到当前步时,前边的树模型已经固定,因此前 K − 1 K-1 K−1步的正则化项 ∑ k = 1 K − 1 Ω ( f k ) \sum_{k=1} ^{K-1}\Omega\left(f_{k}\right) ∑k=1K−1Ω(fk)此时是一个固定的已知常数,可以省去。进一步优化为: L ( K ) = ∑ i = 1 n l ( y i , y ^ i ( K − 1 ) + f K ( x i ) ) + Ω ( f K ) \mathcal{L}^{(K)}=\sum_{i=1}^{n} l\left(y_{i}, \hat{y}_{i}^{(K-1)}+f_{K}\left(\mathrm{x}_{i}\right)\right)+\Omega\left(f_{K}\right) L(K)=i=1∑nl(yi,y^i(K−1)+fK(xi))+Ω(fK)
第 K K K步前的树模型已经固定,它们的正则化项固定,那么前 K − 1 K-1 K−1步的损失是否固定,是什么样的呢?
(3)用泰勒级数近似目标函数:
根据泰勒级数 f ( x ) = f ( x 0 ) 0 ! + f ′ ( x 0 ) 1 ! ( x − x 0 ) + f ′ ′ ( x 0 ) 2 ! ( x − x 0 ) 2 + … + f ( n ) ( x 0 ) n ! ( x − x 0 ) n + O ( f ( n + 1 ) ) f(x)=\frac{f\left(x_{0}\right)}{0 !}+\frac{f^{\prime}\left(x_{0}\right)}{1 !}\left(x-x_{0}\right)+\frac{f^{\prime \prime}\left(x_{0}\right)}{2 !}\left(x-x_{0}\right)^{2}+\ldots+\frac{f^{(n)}\left(x_{0}\right)}{n !}\left(x-x_{0}\right)^{n}+O(f^{(n+1)}) f(x)=0!f(x0)+1!f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+…+n!f(n)(x0)(x−x0)n+O(f(n+1))对目标函数进行近似: L ( K ) ≃ ∑ i = 1 n [ l ( y i , y ^ ( K − 1 ) ) + g i f K ( x i ) + 1 2 h i f K 2 ( x i ) ] + Ω ( f K ) \mathcal{L}^{(K)} \simeq \sum_{i=1}^{n}\left[l\left(y_{i}, \hat{y}^{(K-1)}\right)+g_{i} f_{K}\left(\mathrm{x}_{i}\right)+\frac{1}{2} h_{i} f_{K}^{2}\left(\mathrm{x}_{i}\right)\right]+\Omega\left(f_{K}\right) L(K)≃i=1∑n[l(yi,y^(K−1))+gifK(xi)+21hifK2(xi)]+Ω(fK)其中 g i = ∂ y ^ ( t − 1 ) l ( y i , y ^ ( t − 1 ) ) g_{i}=\partial_{\hat{y}(t-1)} l\left(y_{i}, \hat{y}^{(t-1)}\right) gi=∂y^(t−1)l(yi,y^(t−1))是一阶导数, h i = ∂ y ^ ( t − 1 ) 2 l ( y i , y ^ ( t − 1 ) ) h_{i}=\partial_{\hat{y}^{(t-1)}}^{2} l\left(y_{i}, \hat{y}^{(t-1)}\right) hi=∂y^(t−1)2l(yi,y^(t−1))是二阶导数。此时我们看到前 K − 1 K-1 K−1步的损失函数也被分离出来,在树模型固定的情况下,其损失函数值也是固定的已知常数,因此可以将其省去进一步优化: L ~ ( K ) = ∑ i = 1 n [ g i f K ( x i ) + 1 2 h i f K 2 ( x i ) ] + Ω ( f K ) \tilde{\mathcal{L}}^{(K)}=\sum_{i=1}^{n}\left[g_{i} f_{K}\left(\mathbf{x}_{i}\right)+\frac{1}{2} h_{i} f_{K}^{2}\left(\mathbf{x}_{i}\right)\right]+\Omega\left(f_{K}\right) L~(K)=i=1∑n[gifK(xi)+21hifK2(xi)]+Ω(fK)这样目标函数被优化为只与当前树的划分有关,那么就可以进行逐步计算了。
(4)定义一棵树
对目标函数优化到只与当前步有关时,接下来我们需要关注就是在当前步如何定义一棵树。此时我们先定义几个概念以方便后续的推导:第一个概念是样本所在的节点位置 q ( x ) q(x) q(x),第二个概念是有哪些样本落在节点 j j j上 I j = { i ∣ q ( x i ) = j } I_{j}=\left\{i \mid q\left(\mathbf{x}_{i}\right)=j\right\} Ij={ i∣q(xi)=j},第三个概念是每个结点的预测值 w q ( x ) w_{q(x)} wq(x),第四个概念是由叶子节点的个数以及节点函数值构建的模型复杂度 Ω ( f K ) = γ T + 1 2 λ ∑ j = 1 T w j 2 \Omega\left(f_{K}\right) = \gamma T+\frac{1}{2} \lambda \sum_{j=1}^{T} w_{j}^{2} Ω(fK)=γT+21λ∑j=1Twj2。
如下图例子:
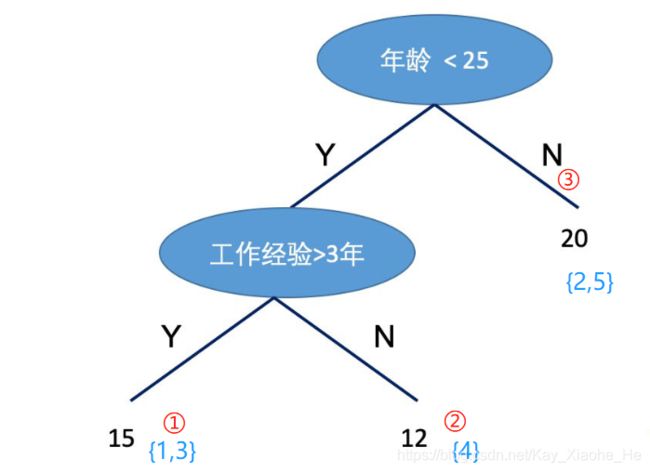
q ( x 1 ) = 1 , q ( x 2 ) = 3 , q ( x 3 ) = 1 , q ( x 4 ) = 2 , q ( x 5 ) = 3 q(x_1) = 1,q(x_2) = 3,q(x_3) = 1,q(x_4) = 2,q(x_5) = 3 q(x1)=1,q(x2)=3,q(x3)=1,q(x4)=2,q(x5)=3, I 1 = { 1 , 3 } , I 2 = { 4 } , I 3 = { 2 , 5 } I_1 = \{1,3\},I_2 = \{4\},I_3 = \{2,5\} I1={ 1,3},I2={ 4},I3={ 2,5}, w = ( 15 , 12 , 20 ) w = (15,12,20) w=(15,12,20)
因此,目标函数可写为
L ~ ( K ) = ∑ i = 1 n [ g i f K ( x i ) + 1 2 h i f K 2 ( x i ) ] + γ T + 1 2 λ ∑ j = 1 T w j 2 = ∑ j = 1 T [ ( ∑ i ∈ I j g i ) w j + 1 2 ( ∑ i ∈ I j h i + λ ) w j 2 ] + γ T \begin{aligned} \tilde{\mathcal{L}}^{(K)} &=\sum_{i=1}^{n}\left[g_{i} f_{K}\left(\mathrm{x}_{i}\right)+\frac{1}{2} h_{i} f_{K}^{2}\left(\mathrm{x}_{i}\right)\right]+\gamma T+\frac{1}{2} \lambda \sum_{j=1}^{T} w_{j}^{2} \\ &=\sum_{j=1}^{T}\left[\left(\sum_{i \in I_{j}} g_{i}\right) w_{j}+\frac{1}{2}\left(\sum_{i \in I_{j}} h_{i}+\lambda\right) w_{j}^{2}\right]+\gamma T \end{aligned} L~(K)=i=1∑n[gifK(xi)+21hifK2(xi)]+γT+21λj=1∑Twj2=j=1∑T⎣⎡⎝⎛i∈Ij∑gi⎠⎞wj+21⎝⎛i∈Ij∑hi+λ⎠⎞wj2⎦⎤+γT
对于当前这颗树,我们的目标就是要最小化目标函数,使它的误差尽量小。现在的目标函数是一个关于 w w w的二次函数。由二次函数 y = a x 2 + b x + c y=ax^2+bx+c y=ax2+bx+c的性质:对称轴 x = − b 2 a x=-\frac{b}{2 a} x=−2ab和极值 y = 4 a c − b 2 4 a y=\frac{4 a c-b^{2}}{4 a} y=4a4ac−b2可知,目标函数的极小值点在: w j ∗ = − ∑ i ∈ I j g i ∑ i ∈ I j h i + λ w_{j}^{*}=-\frac{\sum_{i \in I_{j}} g_{i}}{\sum_{i \in I_{j}} h_{i}+\lambda} wj∗=−∑i∈Ijhi+λ∑i∈Ijgi极小值为: L ~ ( K ) ( q ) = − 1 2 ∑ j = 1 T ( ∑ i ∈ I j g i ) 2 ∑ i ∈ I j h i + λ + γ T \tilde{\mathcal{L}}^{(K)}(q)=-\frac{1}{2} \sum_{j=1}^{T} \frac{\left(\sum_{i \in I_{j}} g_{i}\right)^{2}}{\sum_{i \in I_{j}} h_{i}+\lambda}+\gamma T L~(K)(q)=−21j=1∑T∑i∈Ijhi+λ(∑i∈Ijgi)2+γT
这样就可以对一棵树进行评价了,可是这只是对一棵树整体的评价,我们还不知道怎么构建一棵树,即如何划分结点的方式呢?
(5)构建树:
我们需要像学习决策树一样寻找树的形状,因此我们借助决策树的学习方式,使用目标函数的变化来作为分裂节点的标准。我们使用一个例子来说明:
 例子中有8个样本,分裂方式如图,因此:
例子中有8个样本,分裂方式如图,因此:
L ~ ( o l d ) = − 1 2 [ ( g 7 + g 8 ) 2 H 7 + H 8 + λ + ( g 1 + . . . + g 6 ) 2 H 1 + . . . + H 6 + λ ] + 2 γ L ~ ( n e w ) = − 1 2 [ ( g 7 + g 8 ) 2 H 7 + H 8 + λ + ( g 1 + . . . + g 3 ) 2 H 1 + . . . + H 3 + λ + ( g 4 + . . . + g 6 ) 2 H 4 + . . . + H 6 + λ ] + 3 γ L ~ ( o l d ) − L ~ ( n e w ) = 1 2 [ ( g 1 + . . . + g 3 ) 2 H 1 + . . . + H 3 + λ + ( g 4 + . . . + g 6 ) 2 H 4 + . . . + H 6 + λ − ( g 1 + . . . + g 6 ) 2 h 1 + . . . + h 6 + λ ] − γ \tilde{\mathcal{L}}^{(old)} = -\frac{1}{2}[\frac{(g_7 + g_8)^2}{H_7+H_8 + \lambda} + \frac{(g_1 +...+ g_6)^2}{H_1+...+H_6 + \lambda}] + 2\gamma \\ \tilde{\mathcal{L}}^{(new)} = -\frac{1}{2}[\frac{(g_7 + g_8)^2}{H_7+H_8 + \lambda} + \frac{(g_1 +...+ g_3)^2}{H_1+...+H_3 + \lambda} + \frac{(g_4 +...+ g_6)^2}{H_4+...+H_6 + \lambda}] + 3\gamma\\ \tilde{\mathcal{L}}^{(old)} - \tilde{\mathcal{L}}^{(new)} = \frac{1}{2}[ \frac{(g_1 +...+ g_3)^2}{H_1+...+H_3 + \lambda} + \frac{(g_4 +...+ g_6)^2}{H_4+...+H_6 + \lambda} - \frac{(g_1+...+g_6)^2}{h_1+...+h_6+\lambda}] - \gamma L~(old)=−21[H7+H8+λ(g7+g8)2+H1+...+H6+λ(g1+...+g6)2]+2γL~(new)=−21[H7+H8+λ(g7+g8)2+H1+...+H3+λ(g1+...+g3)2+H4+...+H6+λ(g4+...+g6)2]+3γL~(old)−L~(new)=21[H1+...+H3+λ(g1+...+g3)2+H4+...+H6+λ(g4+...+g6)2−h1+...+h6+λ(g1+...+g6)2]−γ
根据逐步计算的方式,我们现在需要求解的是new的划分,而old树的划分已完成 L ~ ( o l d ) \tilde{\mathcal{L}}^{(old)} L~(old)就成为了一个固定的已知数,因此我们需要最小化 L ~ ( n e w ) \tilde{\mathcal{L}}^{(new)} L~(new)。而 L ~ ( o l d ) − L ~ ( n e w ) \tilde{\mathcal{L}}^{(old)} - \tilde{\mathcal{L}}^{(new)} L~(old)−L~(new)是当前步需要求解的目标函数,因此就需要 m a x { L ~ ( o l d ) − L ~ ( n e w ) } max\{\tilde{\mathcal{L}}^{(old)} - \tilde{\mathcal{L}}^{(new)} \} max{ L~(old)−L~(new)},即:
L split = 1 2 [ ( ∑ i ∈ I L g i ) 2 ∑ i ∈ I L h i + λ + ( ∑ i ∈ I R g i ) 2 ∑ i ∈ I R h i + λ − ( ∑ i ∈ I g i ) 2 ∑ i ∈ I h i + λ ] − γ \mathcal{L}_{\text {split }}=\frac{1}{2}\left[\frac{\left(\sum_{i \in I_{L}} g_{i}\right)^{2}}{\sum_{i \in I_{L}} h_{i}+\lambda}+\frac{\left(\sum_{i \in I_{R}} g_{i}\right)^{2}}{\sum_{i \in I_{R}} h_{i}+\lambda}-\frac{\left(\sum_{i \in I} g_{i}\right)^{2}}{\sum_{i \in I} h_{i}+\lambda}\right]-\gamma Lsplit =21[∑i∈ILhi+λ(∑i∈ILgi)2+∑i∈IRhi+λ(∑i∈IRgi)2−∑i∈Ihi+λ(∑i∈Igi)2]−γ
其中 I L I_L IL为分割节点后左子树的样本集合, I R I_R IR为右子树的样本集合, I I I为根节点的样本集合。
(6)确定最优特征和最优切分点
分割结点的标准确定后就是按照这个标准去寻找最优的特征及最优切分点了,然后依据最优特征和最优切分点对结点进行分裂,形成新的子树。节点分裂是XGBoost在生成新树的过程中,最基本的操作。下面有两种思路。
(6.1)精确贪心分裂算法:
首先找到所有的候选特征及所有的候选切分点, 一一求得其 L s p l i t L_{split} Lsplit , 然后选择 L s p l i t L_{split} Lsplit最大的特征及对应切分点作为最优特征和最优切分点。我们称此种方法为精确贪心算法。该算法是一种启发式算法, 因为在节点分裂时只选择当前最优的分裂策略, 而非全局最优的分裂策略。
精确贪心算法计算过程如下:
输入: 当前结点的样本集 I I I,特征维度 d d d。
输出: 最优分裂
1)初始化分裂收益和梯度统计:
g a i n = 0 , G = ∑ i ∈ I g i , H = ∑ i ∈ I h i gain = 0,\;G=\sum_{i \in I}g_i,\;H=\sum_{i \in I}h_i gain=0,G=i∈I∑gi,H=i∈I∑hi
2)对每个特征 k = 1 , 2 , … , m k=1,2,\dots,m k=1,2,…,m,执行以下步骤:
2.1)初始化左子节点的一阶梯度统计和二阶梯度统计:
G L = 0 , H L = 0 G_L=0,\;H_L=0 GL=0,HL=0
2.2)对结点包含的所有样本在该特征下的取值进行排序,然后遍历每个取值 j j j
a.计算左子节点和右子节点的梯度统计:
G L = G L + g j , H L = H L + h j G R = G − G L , H R = H − H L G_L=G_L+g_j,\;H_L=H_L+h_j\\G_R=G-G_L,\;H_R=H-H_L GL=GL+gj,HL=HL+hjGR=G−GL,HR=H−HL
b.计算最终分裂收益,选取收益最大的:
g a i n = m a x ( g a i n , G L 2 H L + λ + G R 2 H R + λ − G 2 H + λ gain=max(gain,\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda}-\frac{G^2}{H+\lambda} gain=max(gain,HL+λGL2+HR+λGR2−H+λG2
3)按照最大收益的特征及其分裂点进行分裂。
精确贪心算法在选择最优特征和最优切分点时是一种十分有效的方法。它计算了所有特征、所有切分点的收益, 并从中选择了最优的, 从而保证模型能比较好地拟合了训练数据。但是当数据不能完全加载到内存时,精确贪心算法会变得 非常低效,算法在计算过程中需要不断在内存与磁盘之间进行数据交换,这是个非常耗时的过程, 并且在分布式环境中面临同样的问题。
(6.2)基于直方图的近似算法:
为了能够更高效地选择最优特征及切分点,提出了一种基于直方图的近似算法。主要思想是:对某一特征寻找最优切分点时,首先对该特征的所有切分点按分位数 (如百分位) 分桶, 得到一个候选切分点集。特征的每一个切分点都可以分到对应的分桶; 然后,对每个桶计算特征统计 G G G和 H H H得到直方图, G G G为该桶内所有样本一阶特征统计 g g g之和, H H H为该桶内所有样本二阶特征统计 h h h之和; 最后,选择所有候选特征及候选切分点中对应桶的特征统计收益最大的作为最优特征及最优切分点。
基于直方图的近似算法的计算过程如下:
- 对于每个特征 k = 1 , 2 , ⋯ , m , k=1,2, \cdots, m, k=1,2,⋯,m,,按分位数对特征 k k k分桶 Θ \Theta Θ, 可得候选切分点, S k = { S k 1 , S k 2 , ⋯ , S k l } 1 S_{k}=\left\{S_{k 1}, S_{k 2}, \cdots, S_{k l}\right\}^{1} Sk={ Sk1,Sk2,⋯,Skl}1
- 对于每个特征 k = 1 , 2 , ⋯ , m , k=1,2, \cdots, m, k=1,2,⋯,m,,有: G k v ← = ∑ j ∈ { j ∣ s k , v ≥ x j k > s k , v − 1 } g j H k v ← = ∑ j ∈ { j ∣ s k , v ≥ x j k > s k , v − 1 } h j \begin{array}{l} G_{k v} \leftarrow=\sum_{j \in\left\{j \mid s_{k, v} \geq \mathbf{x}_{j k}>s_{k, v-1\;}\right\}} g_{j} \\ H_{k v} \leftarrow=\sum_{j \in\left\{j \mid s_{k, v} \geq \mathbf{x}_{j k}>s_{k, v-1\;}\right\}} h_{j} \end{array} Gkv←=∑j∈{ j∣sk,v≥xjk>sk,v−1}gjHkv←=∑j∈{ j∣sk,v≥xjk>sk,v−1}hj
- 类似精确贪心算法,依据梯度统计找到最大增益的候选切分点。
假设有一个年龄特征,其特征的取值为18、19、21、31、36、37、55、57,我们需要使用近似算法找到年龄这个特征的最佳分裂点:

近似算法实现了两种候选切分点的构建策略:全局策略和本地策略。全局策略是在树构建的初始阶段对每一个特征确定一个候选切分点的集合, 并在该树每一层的节点分裂中均采用此集合计算收益, 整个过程候选切分点集合不改变。本地策略则是在每一次节点分裂时均重新确定候选切分点。全局策略需要更细的分桶才能达到本地策略的精确度, 但全局策略在选取候选切分点集合时比本地策略更简单。在XGBoost系统中, 用户可以根据需求自由选择使用精确贪心算法、近似算法全局策略、近似算法本地策略, 算法均可通过参数进行配置。
1.2 优缺点
XGBoost的主要优点:
1、简单易用。相对其他机器学习库,用户可以轻松使用XGBoost并获得相当不错的效果。
2、高效可扩展。在处理大规模数据集时速度快效果好,对内存等硬件资源要求不高。
3、鲁棒性强。相对于深度学习模型不需要精细调参便能取得接近的效果。
4、XGBoost内部实现提升树模型,可以自动处理缺失值。
XGBoost的主要缺点:
1、相对于深度学习模型无法对时空位置建模,不能很好地捕获图像、语音、文本等高维数据。
2、在拥有海量训练数据,并能找到合适的深度学习模型时,深度学习的精度可以遥遥领先XGBoost。