“泰迪杯”挑战赛 - 基于非侵入式负荷检测与分解的电力数据挖掘（附详细数据及代码）

目录

1. 挖掘背景与目标
   1.1 挖掘背景
   1.2 挖掘目标

2. 问题分析
   2.1 问题 1 的分析
   2.2 问题 2 的分析
   2.3 问题 3 的分析
   2.4 问题 4 的分析

3. 基本假设及符号说明
   3.1 基本假设
   3.2 符号说明

4. 分析方法与过程
   4.1 问题 1 分析方法与过程
   4.1.1 稳态特征库
   4.1.2 暂态特征库
   4.1.3 实时用电量
   4.2 问题 2 分析方法与过程
   4.2.1 模型建立与求解
   4.2.2 结果分析
   4.2.3 实时用电量
   4.3 问题 3 分析方法与过程
   4.3.1 模型建立与求解
   4.3.2 结果分析
   4.3.3 实时用电量
   4.4 问题 4 分析方法与过程
   4.4.1 结果分析
   4.4.2 实时用电量

5. 总结

参考文献

附录

1.挖掘背景与目标

1.1 挖掘背景

随着智能电网的迅速发展，自动化监测各用电设备的不同状态及时段的耗能情况有利于电网方案的制定，进而降低能源消耗，提高能源利用效率。电力分项计量可以对连接到入户线后的建筑物内各个用电设备所消耗的电能进行独立计量，将电器识别作为重要研究方向，从物理层面去查看设备情况，能够实现各用电设备的不同状态及时段的耗能情况的监测。

电力分项计量技术主要分为两种：一种是侵入式电力负荷监测(Intrusive residential load monitoring, ILM)，通过在总负荷内部为每个用电设备配备一个带有数字传感器采集各设备的用电信息。但是安装需要进入到负荷内部，投入较大，效率低，不宜全面推广与应用；另一种是非侵入式电力负荷与分解(Non-IntrusiveLoad Monitoring and Decomposition, NILMD)，其仅需要在用户入口安装一个传感器，通过采集和分析用户的用电总功率或电力掳爱监测每个或每类用电设备的功率及工作状态。为此，NILMD 技术的分项计量技术具有更加简单、经济、可靠等优势，更适用于全面推广与应用。

NILMD 传感器采集到的数据可能是多用电设备耗电数据的叠加结果，如何从海量的、复杂的测量数据中分析并得到各用电设备的运行状态及耗能情况是技术的关键。为此，针对数据特点，利用数据挖掘技术研究非侵入式负荷检测与分解具有重要的意义。

1.2 挖掘目标

(1)根据单一态数据分析各用电设备的运行特征，包括稳态特征和暂态特征，挖掘能够代表数据独特特征的统计量构成设备状态的特征矢量，以此构建特征库。

(2)结合稳态及暂态特征设计特征矢量匹配模型，以实现单一态或者叠加态时各用电设备的识别及相应耗电情况。

2.问题分析

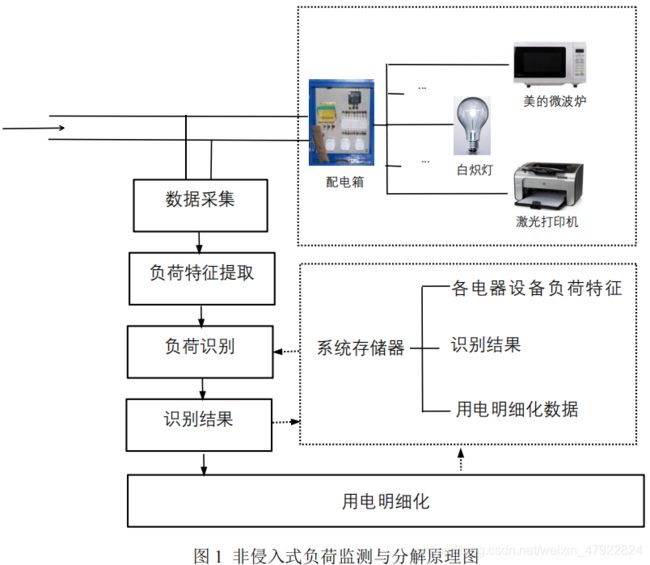
图 1 为非侵入式负荷检测与分解的原理。根据图 1 可知，非侵入式负荷检测与分解的重点即负荷特征提取与识别。

2.1 问题 1 的分析

根据已知数据提取设备及其状态的有效特征并估计实时用电量。附件一中给出了各个设备处于单一态环境下的运行数据，包括电流、电压、功率、周波及谐波等。结合设备操作对各个状态数据的特征进行分析，得到能够代表设备所处状态独特特征的统计量形成特征矢量，以此作为负荷印记，以此构建特征库。其中，稳态负荷印记共同组成了稳态特征库，暂态负荷印记共同组成了暂态特征库。

2.2 问题 2 的分析

根据未知设备的单一态数据，自动识别设备并估计实时用电量。附件二中给出了未知设备处于单一态环境下的运行数据，首先，根据问题 1 中各设备中各个状态特征矢量的统计量提取测试数据的负荷印记，并将其与特征库中的数据进行匹配，认为未知设备即为匹配度最高的那一设备。该问题的难点在于，特征库中只有描述设备中各个状态的负荷印记，没有明确表示设备的印记，为此，在构建未知设备与已知设备匹配度的模型时需要把设备中的所有状态看做一个整体来讨论。

2.3 问题 3 的分析

设备组成分已知，根据设备组叠加态数据，自动识别各设备的状态、操作及操作时间，并估计实时用电量。附件 3 中给出了设备组的运行数据，该数据为不同设备不同状态共同作用的数据，本文称为叠加态数据。该问题的难点在于如何在叠加态数据中剥离出单一态数据，进而完成状态、及操作的匹配，进而确定操作时间。此外，附件 3 中还包含具有操作及操作时间的数据，本文将其视为标准数据，对提出模型的求解结果进行定量分析。

2.4 问题 4 的分析

设备组成分未知情况下，根据设备组叠加态数据，自动识别各设备的状态、操作及操作时间，并估计实时用电量。附件 4 中给出了设备组的运行数据，运用问题 3 中的方法对附件 4 中的数据进行分析，得到各设备的状态、操作及操作时间，并估计实时用电量。

3.基本假设及符号说明

3.1 基本假设

(1)假设数据的绝对准确性，即不考虑温度、湿度等因素对电流、电压以及功率等的影响。

(2)假设待识别设备来自于附件 1 中所给设备。

(3)假设叠加态数据的起始状态无任何设备打开。

3.2 符号说明

4.分析方法与过程

4.1 问题 1 分析方法与过程

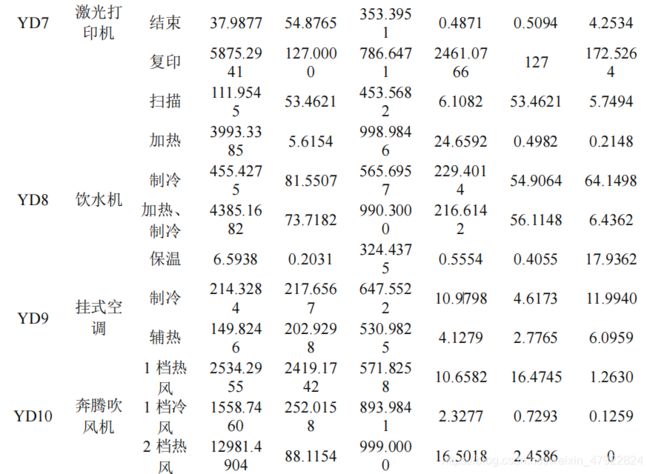
各用电设备由于其构成元件、功能等不同，使设备在运行过程中体现出独特的负荷特性。根据设备的操作及状态可将负荷特性分为稳态特性和暂态特性。稳态特性是用电设备在稳定运行状态时表现出的特性，暂态特性指设备在开、关或状态切换时所表现出的特性。本节将详细讨论附件 1 中各设备的稳态及暂态特性。设备的设备类型及工作参数如表 2 所示。

4.1.1 稳态特征库

(1) 电流电压特性
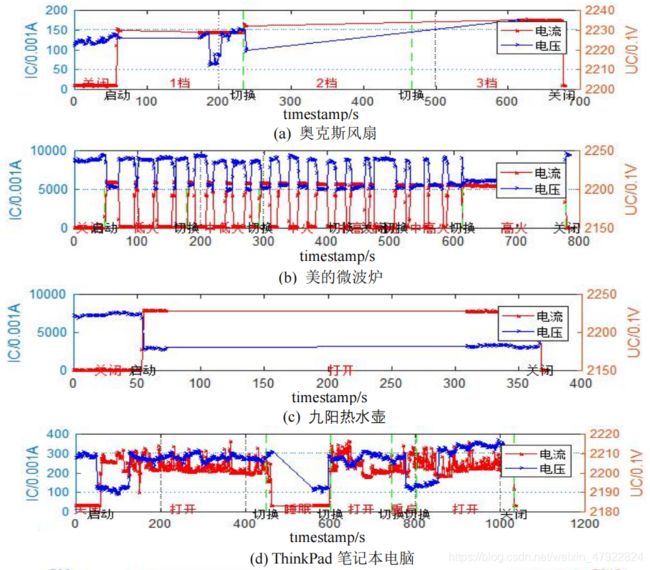
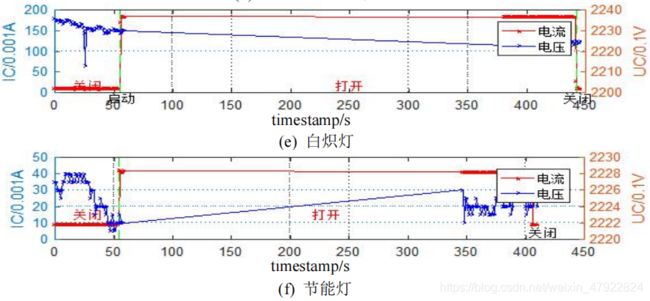
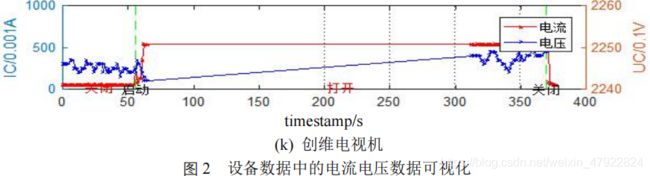
将表 1 中各设备数据中的电流电压数据可视化如图 2 所示，其中(a)-(k)分别表示设备 YD1-YD11。

由图 2 可以看出，各设备的电流及电压波形存在明显差异性，其中，美的微波炉和 ThinkPad 笔记本电脑的电流具有明显的周期性波动的特征，激光打印机、饮水机、挂式空调和奔腾电吹风的电流会随着操作的切换经过一定时间的波动后达到稳定，而奥克斯风扇、九阳热水壶、白炽灯、节能灯和创维电视机的电流均会在切换操作后立即稳定到稳态特征。此外，通过电流纵坐标可以看出，各设备工作的稳态所处的电流具有较大幅度的差异性，例如，具有相似电流波形特征的九阳热水壶、白炽灯和节能灯，其稳态电流分别处于 8000(0.001A)、200(0.001A)和 40(0.001A)。具有明显的可区分性，为此能够用来识别设备及状态。但是，电压波形虽然具有明显差异性，但其波动范围较小，均在 2200(0.1V)左右上下波动，对设备的可区分性较小，为此，本文不单独对电压就行统计分析。

为了反应各设备电流波形之间的差异，对电流波形进行统计分析，利用平均值、均方根、最大值以及范围值等统计量来象征该波形，具体量化公式如下，

平均值：$I(\mu {)}_{ij}=\frac{1}{N}{\sum }_{t=1}^N{I}_{ij}(t),$, 其中，$N$ 为该状态所跨越的时间长度。 (1)

均方根：$I(\sigma {)}_{ij}=\sqrt{\frac{1}{N}{\sum }_{t=1}^N{I}_{ij}(t{)}^2}$。 (2)

最大值：$I(m{)}_{ij}=max{I}_{ij}(t),t=1,...,N$。 （3）

范围值：$I(R{)}_{ij}=max\{I_{ij}(t)\}-min\{I_{ij}(t)\},t=1,...,N$。 （3）

提取的量化结果的特征值如表 3 所示，

(2) PQ 特性
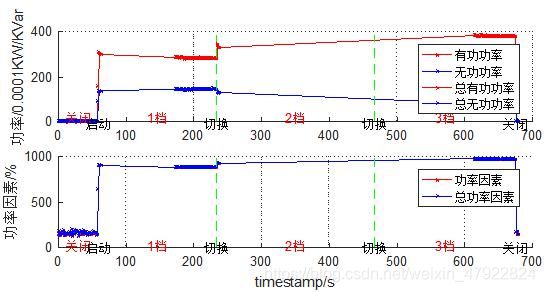
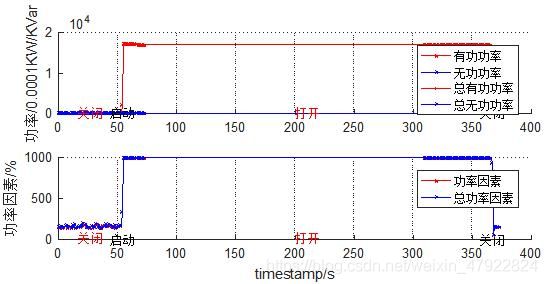
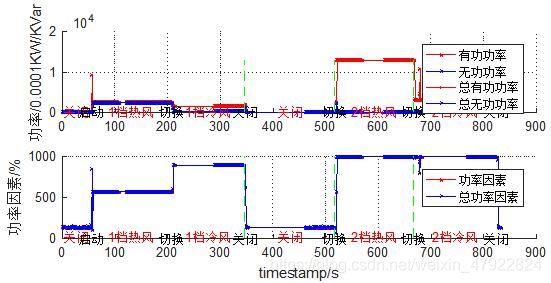
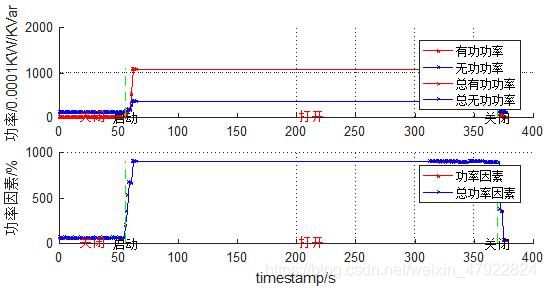
有功功率、无功功率和功率因数是描述设备用电情况必不可少的数据，根据附件 1 中的已知数据将其可视化如图 3 所示，其中(a)-(k)分别表示设备YD1-YD11。

(a) 奥斯卡风扇

(b) 美的微波炉

© 九阳热水壶

(d) ThinkPad 笔记本电脑
(f) 节能灯

(g) FUJI 打印机

==

(h) 饮水机=

(j) 奔腾电吹风

(k) 创维电视机

图 3 设备数据中的有功功率、无功功率和功率因数可视化

由图 3 可知，各设备的有功功率与总有功功率、无功功率与总无功功率、功率因数与总功率因数几乎完全重合，为此，我们只需分析有功功率、无功功率和功率因数就能代表该设备的功率特征。由有功功率、无功功率和功率因数曲线可知，当设备状态处于稳态时，其功率特征是平滑的，只有在状态发生改变时具有波动性，并且其功率各不相同，为此具有可区分性。虽然美的微波炉、ThinkPad笔记本电脑和打印机的功率不平稳，但是其周期性的波段也是能够区别其与其他用电器的重要特点。为了反应各设备功率波形之间的差异，对功率进行统计分析，选取有功功率 P、无功功率 Q 和功率因数 F 组成特征向量，采用稳态时时间序列数据的均值和标准差刻画相应特征，具体量化公式如下，

有功功率平均值: $P_{(\mu )ij}=\frac{1}{N}{\sum }_{t=1}^N{P}_{ij}(t)$, 标准差：$P_{(\sigma )ij}=\sqrt{\frac{1}{N}{\sum }_{t=1}^N(P_{ij}(t)-P_{(\mu )ij}{)}^2}$。（5）

无功功率平均值：$Q_{(\mu )ij}=\frac{1}{N}{\sum }_{t=1}^N{Q}_{ij}(t)$, 标准差：$Q_{(\sigma )ij}=\sqrt{\frac{1}{N}{\sum }_{t=1}^N(Q_{ij}(t)-Q_{(\mu )ij}{)}^2}$。（6）

功率因数平均值：$F_{(\mu )ij}=\frac{1}{N}{\sum }_{t=1}^N{F}_{ij}(t)$, 标准差：$F_{(\sigma )ij}=\sqrt{\frac{1}{N}{\sum }_{t=1}^N(F_{ij}(t)-F_{(\mu )ij}{)}^2}$。（7）

根据状态稳定时的功率均值 P(μ)、Q(μ)、F(μ)和方差 P(σ)、Q(σ)、F(σ)构建功率特征矢量如表 4 所示，

为了探究提取特征的可信度，将提取后的特征矢量在三维坐标中表示如图 4所示，其中不同形状表示不同设备，不同颜色表示该设备所处的不同状态。

由图 4 可知，不同设备的不同状态的功率具有聚类的性质，为此采用均值代替该状态特征的行为是有效的，通过图 4 分析可知，功率特征矢量对大多数设备的状态均能实现较好区分。

(3) 瞬时功率特性
根据物理学定义，瞬时功率定义为电压与电流的乘积，
$P_{ij}(t)=U_{ij}\cdot I_{ij}(t)$。（8）

根据附件已知数据，绘制各设备各状态的瞬时功率曲线如图 5 所示，

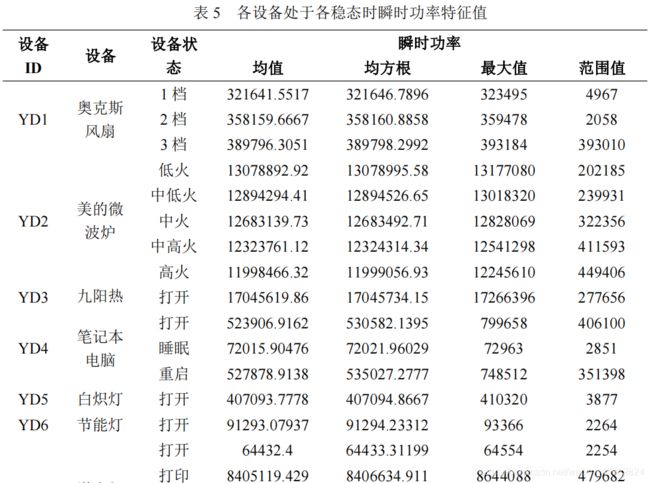
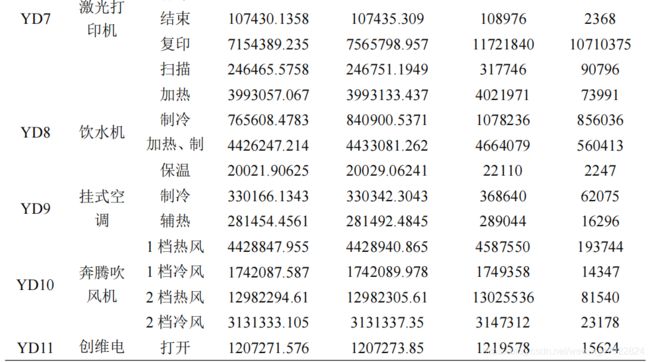
由图 5 可知，各设备各状态的瞬时功率具有明显的差异性，提取曲线特征得到特性值列于表 5

(4) 周波 U-I 特性

首先对周波数据进行预处理，然后将处理后的电压数据作为 x 轴，电流数据作为 y 周，时间序列为 z 轴绘制 U-I 曲线，单位分别为 0.1V 和 0.0001A，U-I 曲线可以从图形角度反应出设备谐波含量的高低。每一时间点有 128 个采样点，可以构成一个几何图像，不同状态的曲线的几何特征不同，为此通过分析周波曲线U-I 特性，构建特征矢量进而区分设备及状态是可行的。例如，对于电阻负载其U-I 图像是一条直线；感性容性负载其 U-I 曲线是一个椭圆；则每一个用电设备的操作对应的 U-I 曲线如下图 6 所示，其中，其中(a)-(k)分别表示设备 YD1-YD11。


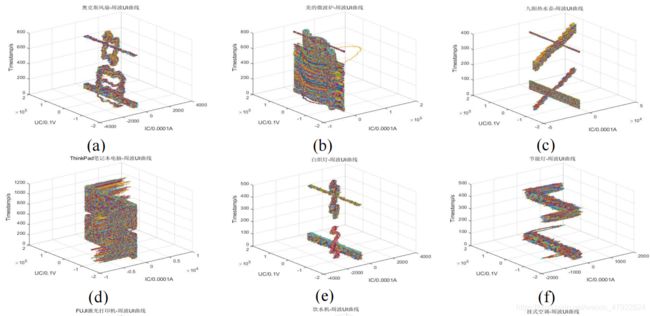
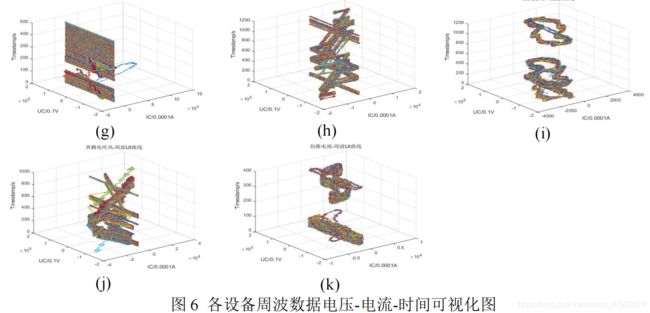
由图 6 可知，U-I 曲线特征子啊同一状态的多个时间点上的曲线特性一只，随着状态的改变，曲线特性也随之变化，将其时间序列简化到一个时刻刻的 U-I曲线如图 7 所示。



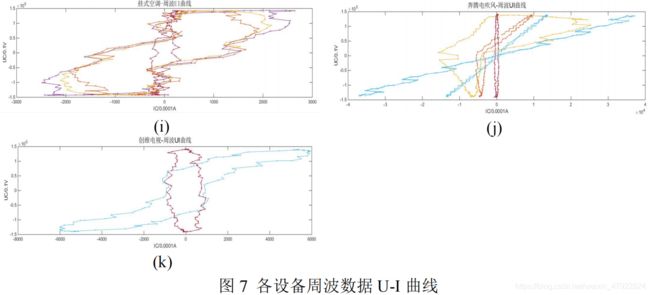
由图 7 可以看出不同用电设备的不同操作 U-I 曲线具有明显的差异，采用矩形对曲线划分并进行量化。选取电压差，电流差及其比值作为区分不同设备得一个特征。以创维电视为例，如图 8 所示，红框和绿框分别表示 U、I 范围值，中间的斜对角连线为其斜率。

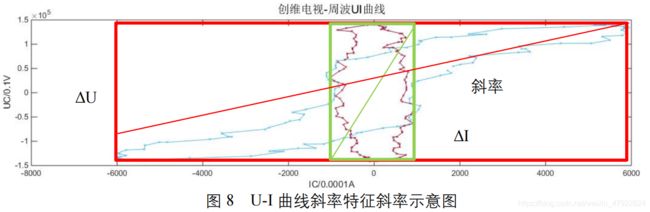
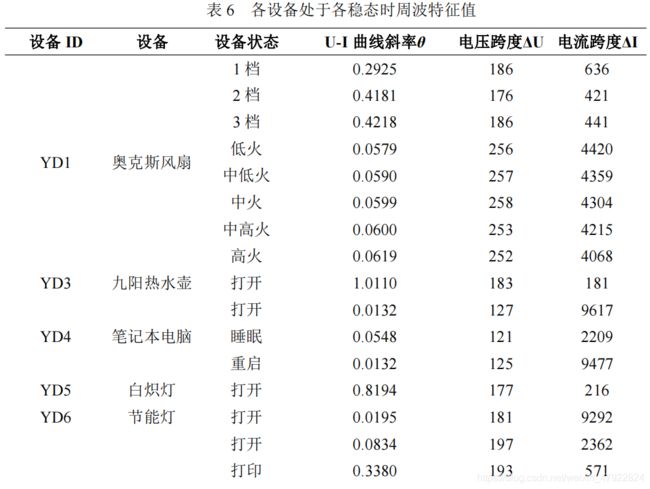
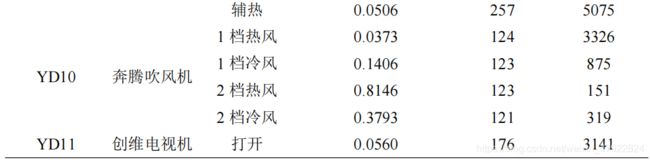
结合 U-I 曲线斜率及坐标跨度，构建周波特征矢量如表 6 所示，其计算方式如下：

电流跨度：$\Delta I_{ij}=max\{\mu [C_{I_{ij}}^l(t)]-min\{\mu [C_{I_{ij}}^l(t)],t=1,...,N,l=1,...,{128_{ij}}^l(t)$, 其中，$C_{I_{ij}}^l(t)$表示设备 $i$ 第$j$个状态周波中第 $l$ 次的电流数据，$\mu [\cdot ]$表示均值操作符。 (9)

电压跨度：$\Delta U_{ij}=max\{\mu [C_{U_{ij}}^l(t)]-min\{\mu [C_{U_{ij}}^l(t)],t=1,...,N,l=1,...,128$, 其中，$C_{U_{ij}}^l(t)$表示设备 $i$ 第$j$个状态周波中第 $l$ 次的电压数据。(10)

U-1曲线斜率：${\theta }_{ij}=\frac{\Delta U_{ij}}{\Delta I_{ij}}$。 （11）

提取的量化结果的特征值如表 6 所示，



(5) 谐波特性

谐波表示电流信息的畸变程度，电流畸变程度越大，谐波含量越丰富，不同设备的谐波含量不同，通过分析可知，偶次谐波含量较差，不足够反应设备特性。由于数据量较大，能够反映谐波特性的有效点有限，为了避免冗余数据的影响，需要将原始谐波数据进行 PCA 降维处理，然后取前 3 个主成分用来代替该数据特征。

首先，计算每个时刻点的谐波数据的均值$\overline{H_i}=\frac{1}{T}{\sum }_{t=1}^T{H}_i(t)$, 其中，T 表示时间长度。根据均值计算特征协方差矩阵，

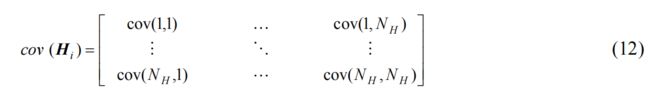
其中，$N_H$表示数据维度。然后，计算协方差矩阵的特征值λ和特征向量ξ，将特征向量按特征值从小到大进行排序，取得前 3 个向量构成特征向量矩阵，然后将原数据投影到选取的特征向量上得到 PCA 降维后的结果。将降维结果展示在三维空间如图 9 所示。

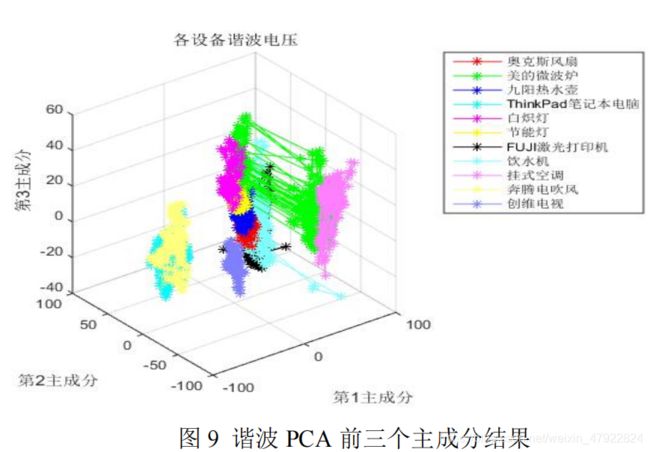
由图 9 可知，同一设备的状态空间可能较为分散，例如，绿色的所表示的美的微波炉。针对此现象，本文根据高斯混合模型原理(Gaussian Minxture Model, GMM)结合 Mean-Shift 算法对各主成分进行了浓缩。假设该设备有 $N_p$ 个混合模型分量，则$P_i={\sum }_p^{N_p}{\pi }_p{P}_{ip}$, 其中，$P_i$表示第 $i$个设备的谐波信息，$P_{ip}$表示第 $i$ 个设备的第 $p$ 个混合模型分量，${\pi }_p$为第 $p$ 个混合分量的权重。

Mean-Shift 算法是一种高效的统计迭代聚类算法，由非参数密度估计公式推导获得，能在特征空间中沿着采样点密度分布上升的方向搜索到局部密度极值点，收敛到同一极值的点聚为一类。如图 10 直观的刻画了 Mean-Shift 算法的聚类过程，$x_i^0$表示初始数据集迭代中心点，通过 Mean-Shift 算法计算以$x_i^0$为中心的圆形区域内的 Mean-Shift 向量，即 $x_i^0$点移动的步长，$x_i^0$点通过计算移动到点$x_i^1$的位置，相同的算法使 $x_i^1$移动到点 $x_i^2$，通过反复计算，最终初始点 $x_i^0$移动到密度最大点 $x_i^n$处。而聚类过程中主要是寻找聚类中心点，即特征空间的密度的局部最大值点，由 Mean-Shift 基本原理可知，Mean-Shift 方法能够在任何特征
空间的数据中通过 Mean-Shift 矢量迭代来定位密度的最大值点，并且在聚类过程中不需要假设数据符合特定的分布，也不需要我们预先设置聚类中心的个数，并且 Mean-Shift 聚类结果也不依赖于初始点的选取，具有一定的确定性。

如果样本点 $x_i$是从一个概率密度函数 f(x)中采样得到，那么由于非零的概率密度梯度指向概率密度增加最大的方向，因此从平均上来说，$S_h$区域内的样本点更多的落在沿概率密度梯度方向。综上所述，偏移向量相应的也指向概率密度梯度的方向，如图 11 所示。

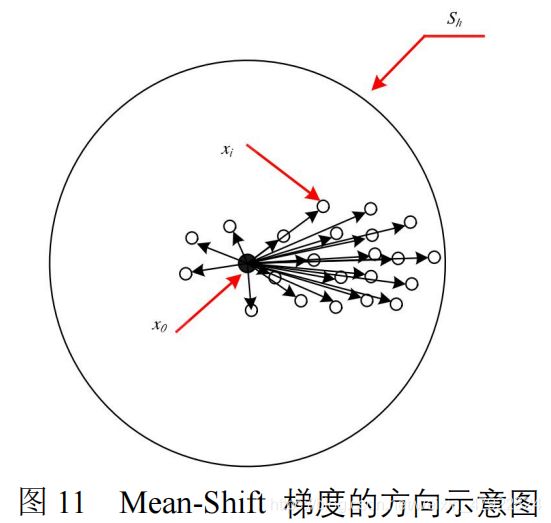
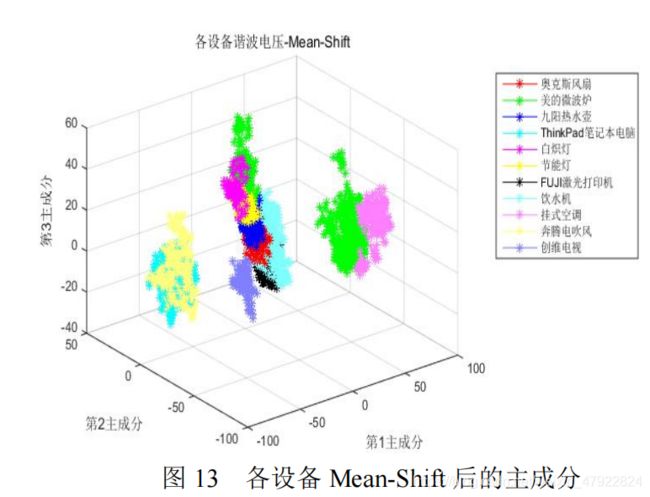
图 12 为各设备主成分经 Mean-Shift 后各分量的结果，其中不同颜色表示不同混合模型分量。各设备的经 Mean-Shift 处理后的数据显示结果如图 13 所示。并将数据列于表 7。由表 7 可知，设备运行时耗电数据越复杂，其混合模型分量越多。

4.1.2 暂态特征库

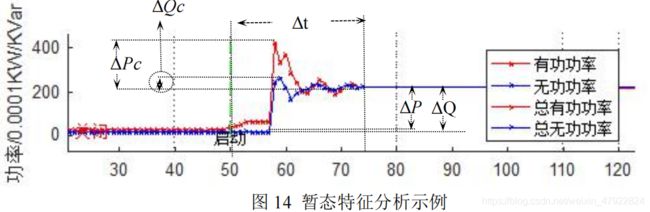
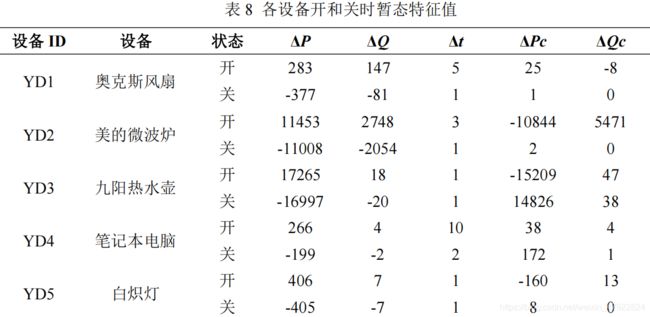
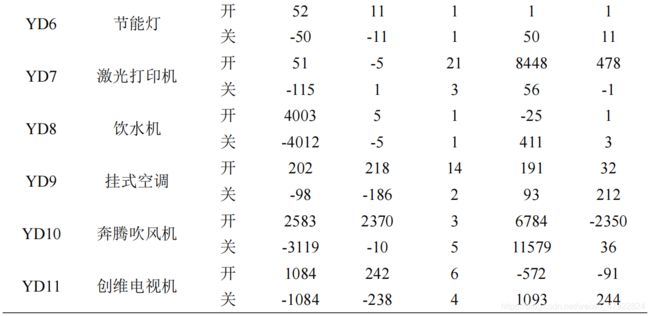
根据 4.2.1 节中各设备数据的可视化结果可知，各用电设备开启到达稳定具有一定的过程，我们称之为暂态。如图 14 所示，以挂式空调启动时的功率为例，分析暂态特性。这个过程所需的时间各不相同，并且过程中功率等变化也具有独特的特征，设备开和关时的功率变化尤为明显。结合暂态所需时间Δt，有功功率跳变量ΔP，无功功率跳变量ΔQ，以及暂态中最大有功功率与暂态后有功功率之差ΔPc 及暂态中最大无功功率与暂态后无功功率之差ΔQc 定义暂态特征矢量，构建暂态特征库。提取量化结果特征值如表 8 所示。

4.1.3 实时用电量

根据物理学定义，用电量的计算公式为，
$W_i(t)=U_i(t)\cdot I_i(t)\cdot t_i$。（13)

其中，$U_i(t)$为第 $i$ 个设备 $t$ 时刻的电压，$I_i(t)$为第 $i$ 个设备 $t$ 时刻的电流，$t_i$第 $i$ 个设备的时间。

附件中所给数据在部分时间点上存在空缺，针对在时间序列上采集的功率数据会出现的空缺值的问题，通过分析，空缺值并不是真的没有负载，而是因为采集设备的特性导致的。由此可以得出，排除开始时间段的未负载情况，在用电设备经负载之后出现空缺值时刻是处于工作状态的，如下图 15 用电模拟图所示，其中白色表示未工作，红色表示负载有数据，黄色表示负载无数据，并用 0 表示无数据，1 表示有数据。在[0，1]时间内用电器处于未工作状态，在[2，10]时间段内是处于工作状态，空缺值为 4，7 和 8 时刻。

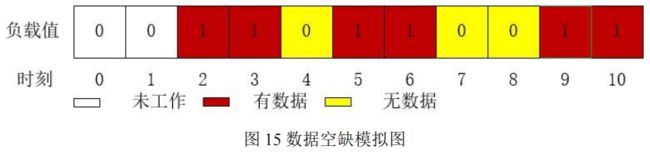
为了解决负载情况下出现的空缺值问题，本文设计了线性插值算法，如下图 16插值模拟图所示，

其中左图为线性插值示意图，7，8 时刻为空缺值，利用已有的数据即 5，6 时刻的值求解空缺值，建立数学表达式为，

$\frac{h_6-h_5}{x_6-x_5}=\frac{h_7-h_6}{x_7-x_6}$。 （14）

其中时间序列差值为 1 秒，即 x6-x5和 x7-x6为 1 秒，利用已知量 h6，h5求解 h7的值，采用该方法可以有效解决空缺值问题。

将空缺值解决之后，实时用电量表示为，
$W_i(t)=U_i(t)\cdot I_i(t)\cdot t_i\times 10000÷3600$。（15）

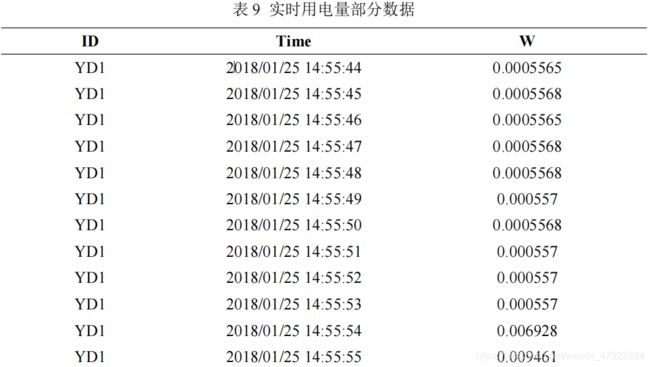
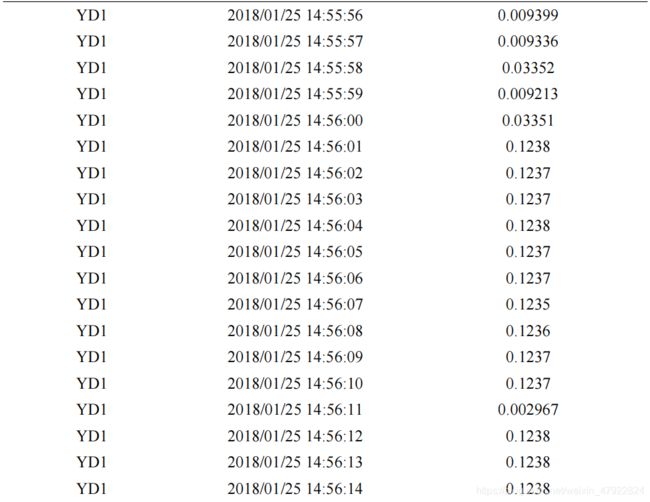
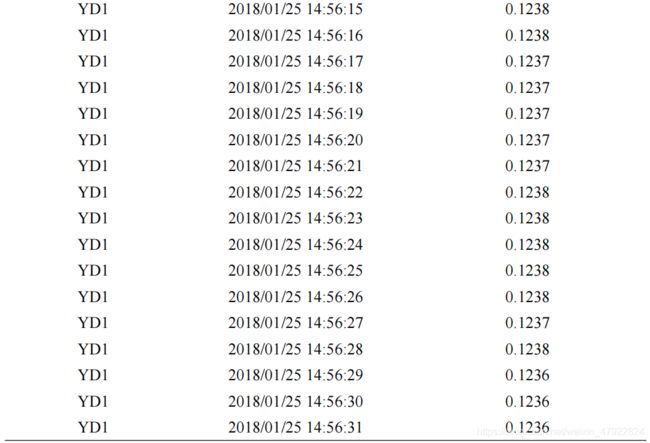
其中，$W_i(t)$为第 $i$ 个设备的实时用电量，单位为 0.001KWh。由题意知电流的单位 0.001A，电压的单位是 0.1V，故在计算实时用电量时还需要单位转换，如公式(15)所示。最后将各设备的实时用电量的具有代表性的时刻列与表 9，整体实时用电量见附件。

4.2 问题 2 分析方法与过程

本节的主要任务是根据已知时间序列的电流、电压、功率、周波和谐波等数据自动识别用电设备。首先利用最小生成树原理确定未知设备时间序列数据中哪部分是稳态，哪部分是暂态，然后提取相应稳态及暂态负荷印记，利用多维空间欧氏距离定义非相似性测度，将其与问题 1 构建的稳态及暂态特征库中的数据进行匹配，距离值越小，说明匹配率越高。认为未知设备属于匹配率最高的那一设备，以此完成用电设备的自定识别。

4.2.1 模型建立与求解

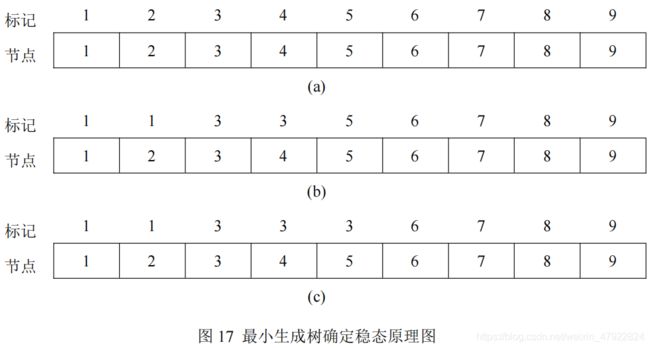
已知一未知设备的时间序列测试数据，将时间序列 $T=T_t,t=1,...,T$中的 $T_t$视为最小生成树中的节点，相邻时间节点上的有功功率的差值与时间间隔的比作为边的权重，即，$w_{tt’}=P(t)-P(t’)$，其中，t’ = t+1。按顺序对每个生成树的节点进行标记，即 $L=L_t,t=1,...,T$，且 $L_t\in 1,...,T$，将权值 $w_{t{t}^{\prime }}$由小到大排列，并依次合并权值最小的两个节点，其原理如图 17 所示，其中图 17(a)为节点及其标记的初始状态，图 17(b)为合并第 1、2 个节点时的标记状态，图 17©为依次合并节点 3、4、5 时的标记状态。合并条件为合并后两个节点所处状态的功率的方差σ($P_{tt’}$)与合并前二者方差σ($P_t$)、σ($P_t’$)的和的差值是否小于给定阈值δ，即
$\sigma (P_{t{t}^{\prime }})-(\sigma (P_t))+\sigma (P_{t^{\prime }})<\delta$。（16）

其中，Ptt’表示合并后两节点的功率。

当所有节点均合并完毕后，原始时间序列会被划分为若干个稳态段及暂态段，如图 18所示。图中蓝色为测试数据时间序列的功率走势图，绿色为采用最小生成树法检测到的稳态时间段。

假设从测试数据 $i’$中识别出了 $k$ 个稳态，$S_i’=S_{i’h},h=1,...,k$，其中，$h$ 为稳态状态索引，$S_{i’h}$为测试数据 $i’$处于第 $h$ 个稳态时的稳态特征矢量。利用多维空间欧氏距离测度定义测试数据 $i’$与已知设备 i 之间的非相似性 $d_{i’i}$为，

$d_{i’i}$值越小，说明测试数据 $i’$与已知设备 $i$ 匹配度越高，则测试数据 $i’$的 ID 为，

4.2.2 结果分析

根据上述方法，得到设备 1 中有 4 个稳态(其中第一个状态变化太小，图中显示不明显)，设备 2 中有 3 个稳态，如图 19 所示。


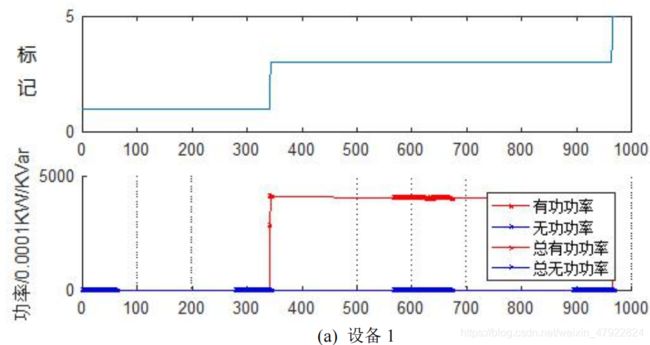
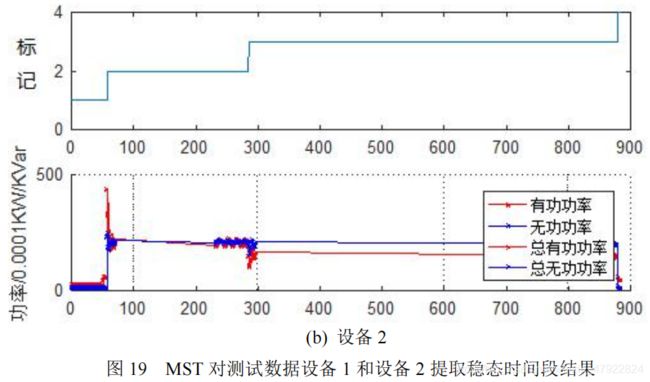
去除开启前和关闭后的关闭状态，各设备包含 2 个稳态特征。提取各设备的稳态特征矢量如表 10 所示。由于谐波数据均为 0，不能提供信，所以本次特征矢量中不考虑谐波特征。考虑到电流和瞬时功率均值与均方根较接近，为此在均方根和均值中选取均方根作为特征量。

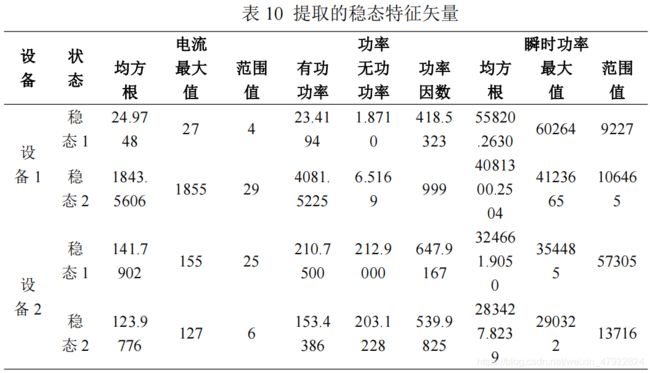
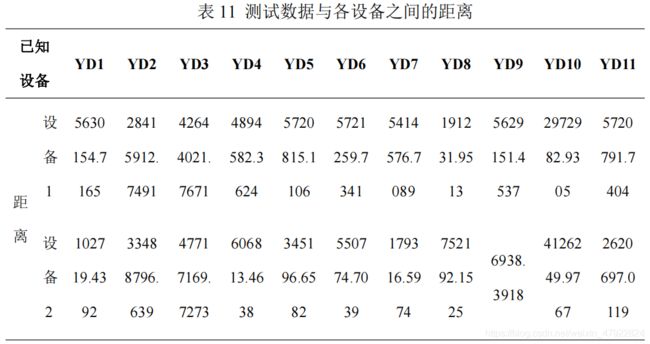
将上述特征与第一问中的各设备的稳态特征库按照公式（17）进行匹配，得到测试数据与各设备之间的距离如表 11 所示。由表 11 可知，其中设备 1 和设备2 与各已知设备的距离最小值为 191231.9513 和 6938.3918，分别对应于设备 YD8和 YD9，因此，我们认为设备 1 为 YD8，即饮水机，设备 2 为 YD9，即挂式空调。

4.2.3 实时用电量

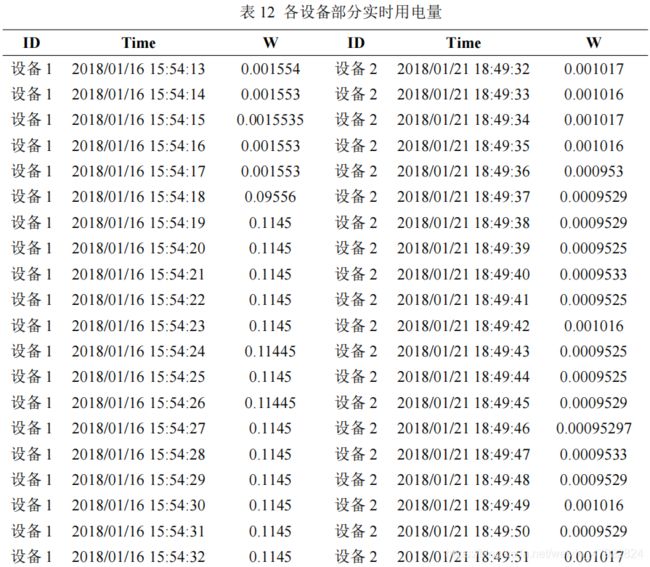
根据问题 1 中估计实时用电量的方法，得到设备 1 和设备 2 的部分实时用电量如表 12 所示。(整体见附件)

4.3 问题 3 分析方法与过程

由于在叠加态数据中最具明显变化特征的即功率，通过分析发现，功率随着状态的改变呈现加性叠加关系，在叠加态中容易剥离得到各个设备的单一态信息，为此本节将重点基于功率研究各设备的状态与操作识别。

4.3.1 模型建立与求解

本节的主要任务是在叠加态数据中识别出各设备的运行状态，首先根据问题2 中的最小生成树方法检测各设备的稳态时间区间，如图 20 所示。其中，图20(a)-(f)分别表示设备组 1-6。





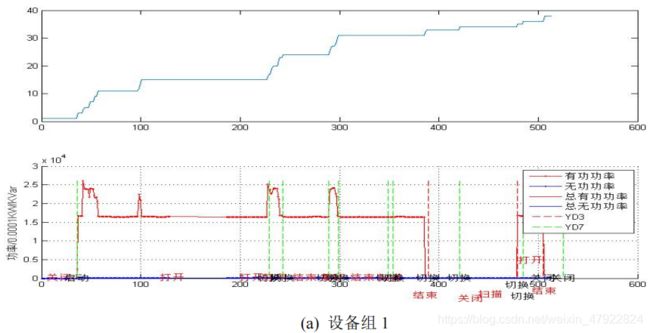
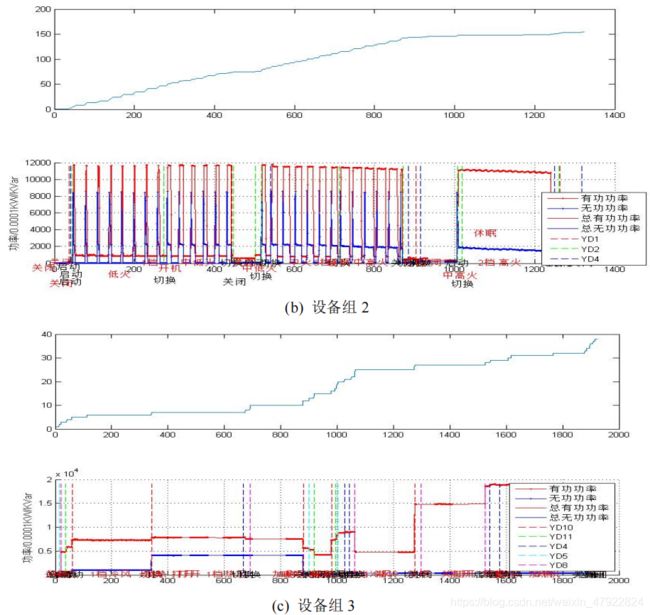
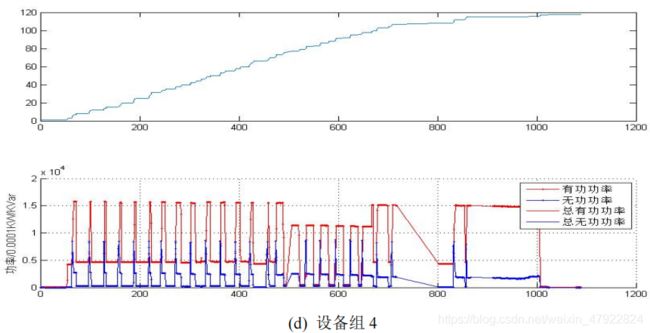
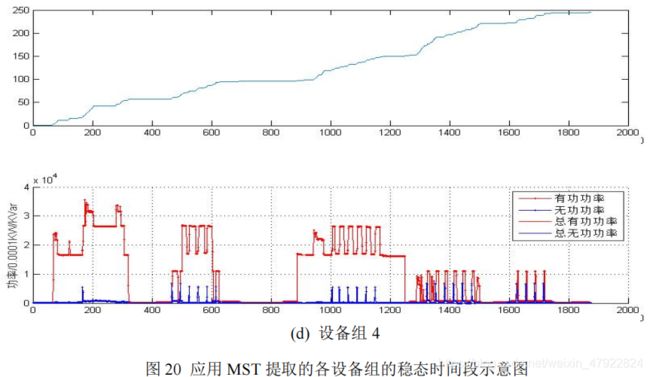
假设各设备的各个状态的功率服从均值为μ，标准差为σ的高斯分布，即
$p(x|\mu ,\sigma )=\frac{1}{\sqrt{2\pi \sigma }}exp\{-\frac{(x-\mu {)}^2}{2{\sigma }^2}\}$。 （19）

假设对于一个未知设备的时间序列数据，共检测出 $k$ 个平滑稳态，$S_i^{\prime }=\{S_{i’h},h=1,...,k\}$，其中，$h$ 为稳态状态索引。计算平滑稳态中的功率数据 $P_{Si}$ 属于各个设备的状态的概率，即

$p(P{s}_i|\mu (P_{ij}),\sigma (P_{ij}))=\frac{1}{\sqrt{2\pi }\sigma (P_{ij})}exp\{-\frac{(P{s}_i-\mu (P_{ij}){)}^2}{2\sigma (P_{ij}{)}^2}\}$。 （20）

其中，μ($P_{ij}$)和σ($P_{ij}$)分别为第 $i$ 个设备中第 $j$个状态的功率的均值及方差。则该平滑状态属于概率最大的那一状态，即

4.3.2 结果分析

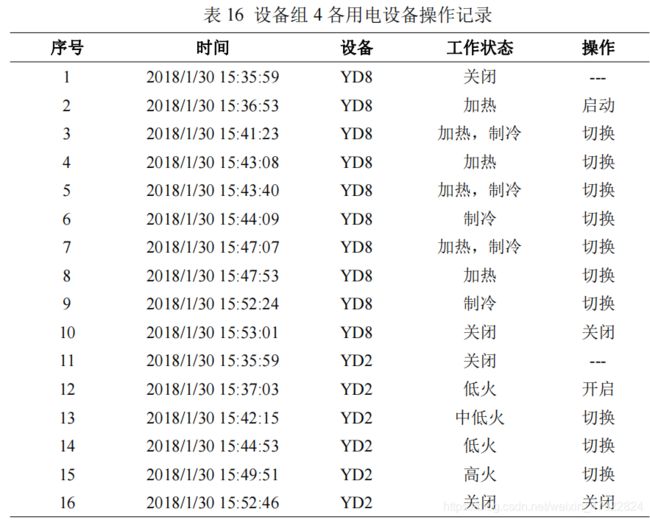
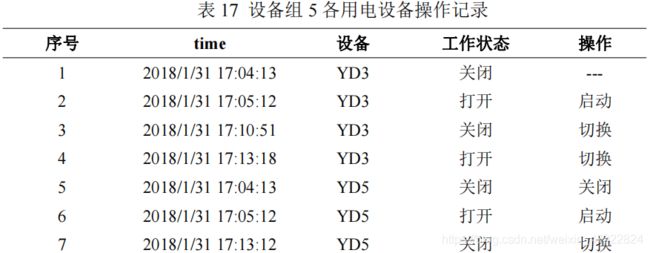
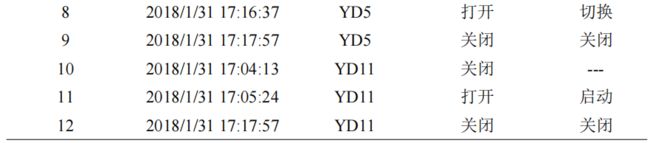
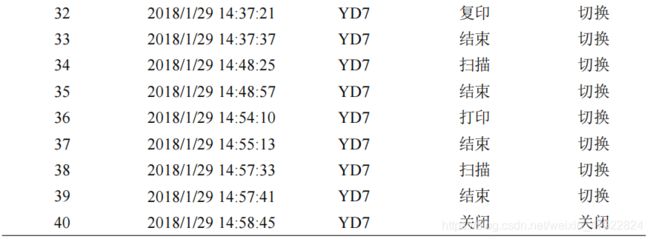
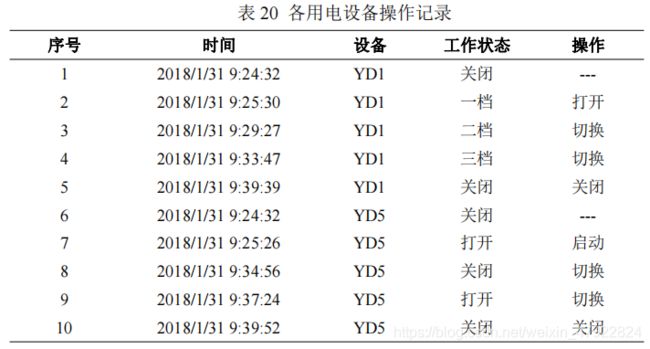
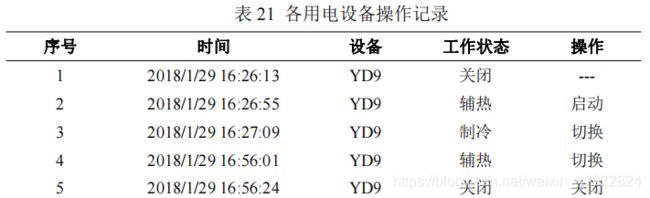
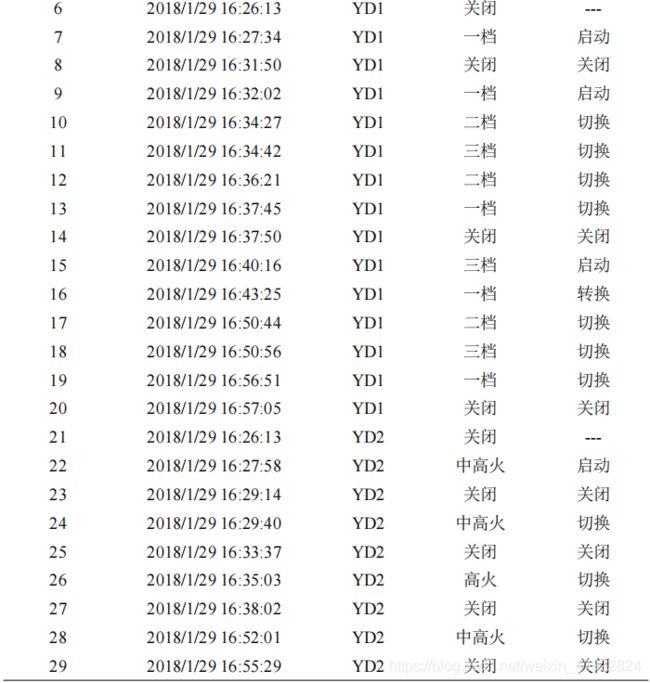
根据公式(20)和(21)解译各设备的状态、操作及操作时间如表 13-18 所示。

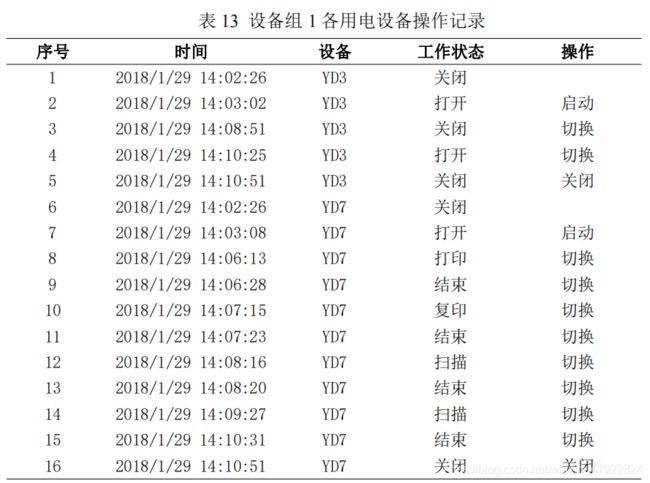
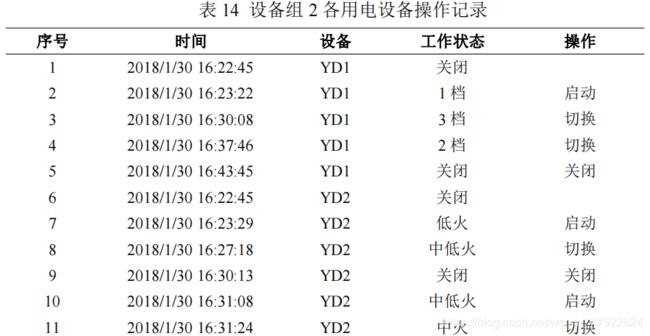
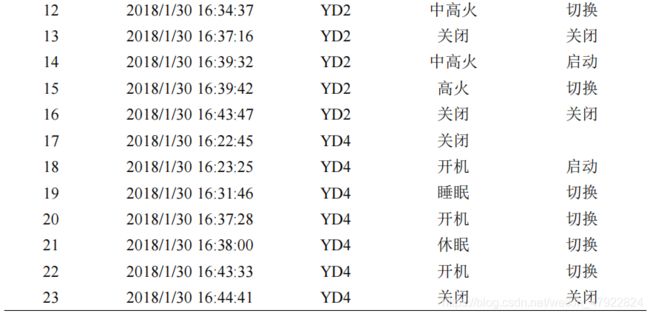
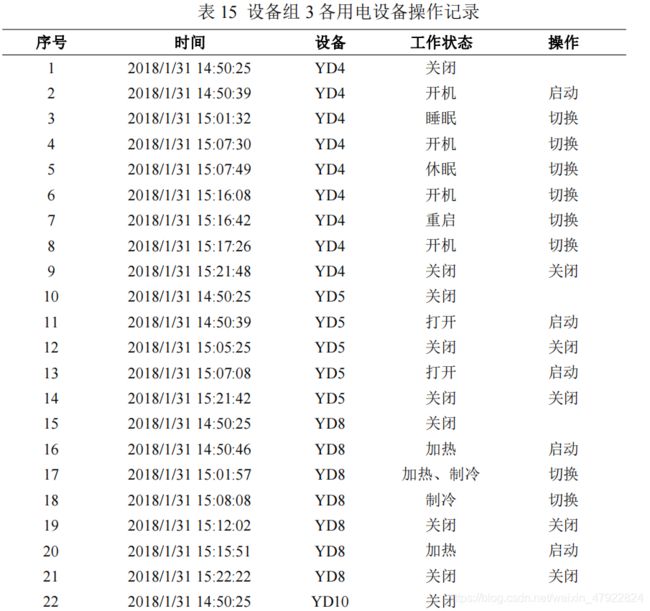
4.3.3 实时用电量

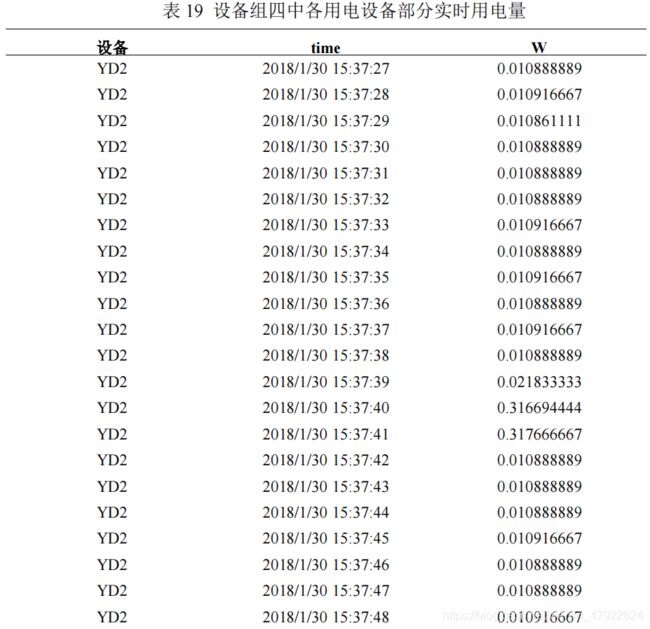
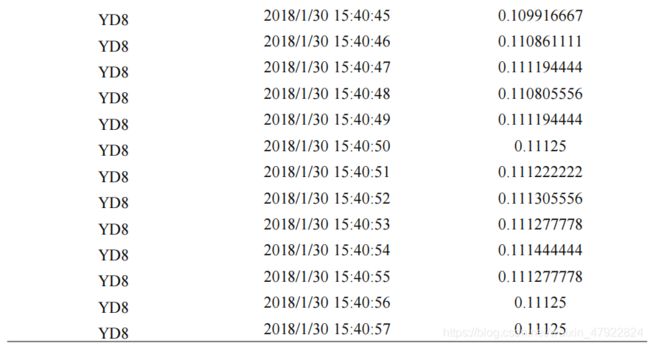
由于叠加态的特性，本节采用 W=Pt 估计设备的实时用电量。结合设备及其操作，得到设备组中各设备的实时用电量如表 19 所示(以设备组四为例)。

4.4 问题 4 分析方法与过程

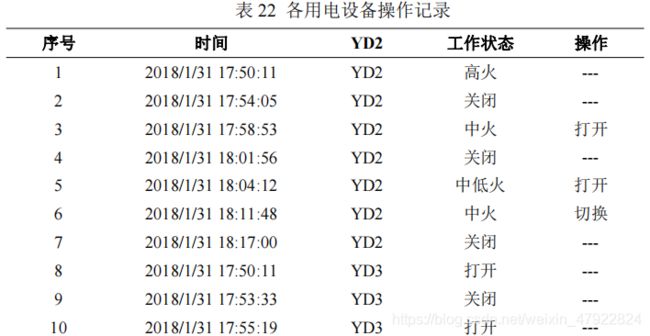
4.4.1 结果分析

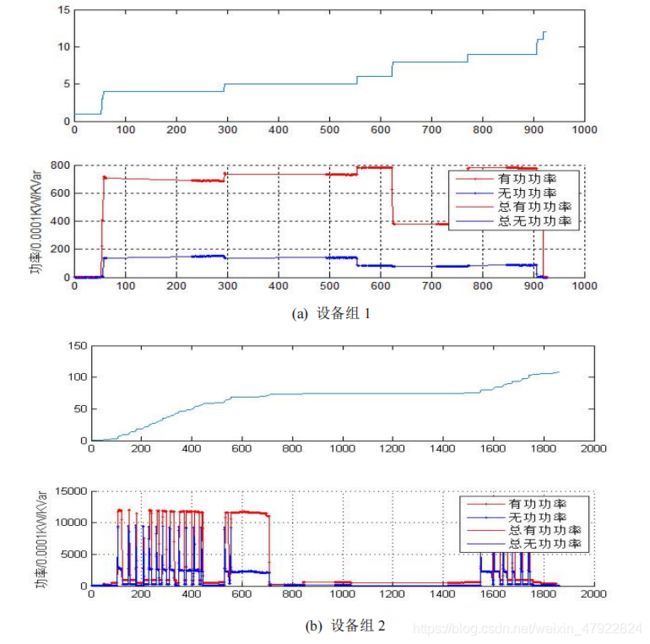
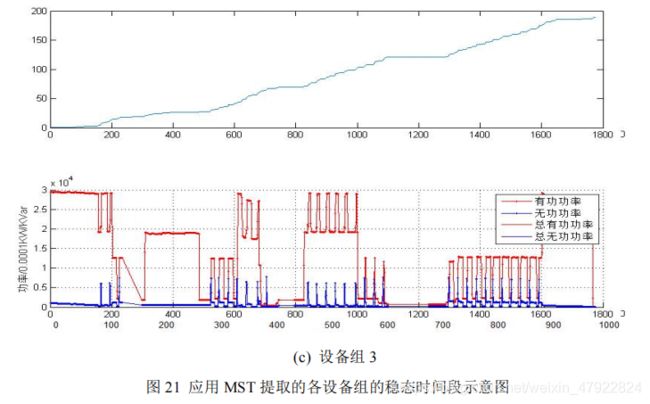
利用最小生成树方法检测各设备的稳态时间区间，如图 21 所示。其中，图21(a)-©分别表示设备组 1-3。

4.4.2 实时用电量

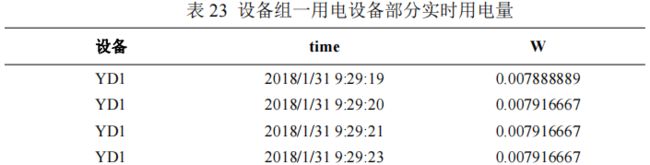
以设备组一为例。设备组一中各设备部分实时用电量如表 23 所示。

5.总结

本文的主要目的利用数据挖掘与数学建模技术实现非侵入式负荷检测与分解。首先，通过对各设备的电流、电压、功率、周波、谐波等数据进行可视化，然后从中提取能够代表各数据独特特征的统计量共同构成负荷印记特征库。为后续设备及其状态识别做准备。

对于未知设备的时间序列数据，首先，利用 MST 原理实现对测试数据稳态时间段的检测，将各个时间视为生成树的节点，利用功率变化量描述两节点连接边的权重，通过判断一次连接权重较小的节点，最后得到若干个时间序列段，即检测到的稳态时间段。然后，提取稳态时间段上数据的特征量，将其与稳态特征库进行匹配，以完成设备及其状态的识别。对于单一态数据的设备的识别需考虑识别出的稳态特征与各个设备内状态的特征的关系，进而定义未知设备与已知设备的距离，我们认为该设备属于距离最小的那一设备。对于叠加态数据，首先需要剥离出各设备的单一态的功率，假设同一状态的数据服从一类高斯分布，判断提取出的平稳状态属于已知设备状态的概率，认为该平稳状态属于概率最大的那一状态。最后，得出各用电设备及其状态、操作合操作时间，并结合操作估计各用电设备的实时用电量。

参考文献

[1] 李雨轩. 非侵入式负荷分解算法的综合研究[D].北京交通大学,2016.

[2] 余 贻 鑫 ,刘 博 ,栾 文 鹏 .非 侵 入 式 居 民 电 力 负 荷 监 测 与 分 解 技 术 [J]. 南 方 电 网 技术,2013,7(04):1-5.

[3] Liang J, Simon K.K.Ng, et al. Load Signature Study–Part I: Basic Concept, Structure, and Methodology [J]. IEEE Transactions on Power Delivery, April 2010, 25(2): 551-560.

[4] 黎灿兵, 曲芳, 王晓宁等. 基于模糊聚类的电力系统负荷特性分 析[J]. 郑州大学学报
(工学版), 2010, 31(01): 107-110.

[5] 丁世敬,王晓静,雍静等.基于事件检测的非侵入式负荷识别方法研究 [J]. 建筑电气, 2017, 36(07): 57-64.

[6] Lam H.Y, Fung G.S.K. A Novel Method to Construct Taxonomy of Electrical Appliances Based on Load Signatures [J]. IEEE Transactions on Consumer Electronics, 2007, 53: 653 -660.

[7] 李刚, 于长海, 王天军等. 居民负荷设备的非侵入式识别方法研究 [J].电力信息与通信
技术, 2017, 15(05): 54-60.

[8] 杨甲甲, 赵俊华, 文福拴等. 智能电网环境下基于大数据挖掘的居民负荷设备识别与负
荷建模 [J].电力建设, 2016, 37(12): 11-23.

[9] Lee K.D. Electrical Load Information System Based on Non-intrusive Power Monitoring [D]. Department of Mechanical Engineering, Massachusetts Institute of Technology, 2003.

[10] Hart G.W. Residential Energy Monitoring and Computerized Surveillance Via Utility Power Flows [J]. IEEE Technology and Society, June 1989: 12-16.

附录

function DataReader()
%% 读取所有数据
%读取附件 1 数据
sheet1 = {
     '设备数据','周波数据','谐波数据','操作记录'};
sheet2 = {
     '设备数据','周波数据','谐波数据'};
Att1 = cell(11,1);%附件 1 数据
Equipment.FileName = 'YD1';
Equipment.Name = '奥克斯风扇';
Equipment.Desc = '220V,60W';
Att1{
     1} = Equipment;
Equipment.FileName = 'YD2';
Equipment.Name = '美的微波炉';
Equipment.Desc = '220V,输入：1150W，输出：700W';
Att1{
     2} = Equipment;
Equipment.FileName = 'YD3';
Equipment.Name = '九阳热水壶';
Equipment.Desc = '220V,1800W';
Att1{
     3} = Equipment;
Equipment.FileName = 'YD4';
Equipment.Name = 'ThinkPad 笔记本电脑';
Equipment.Desc = '220V,3.25A/4.5A';
Att1{
     4} = Equipment;
Equipment.FileName = 'YD5';
Equipment.Name = '白炽灯';
Equipment.Desc = '220V,40W';
Att1{
     5} = Equipment;
Equipment.FileName = 'YD6';
Equipment.Name = '节能灯';
Equipment.Desc = '220V,5W';
Att1{
     6} = Equipment;
Equipment.FileName = 'YD7';
Equipment.Name = 'FUJI 激光打印机';
Equipment.Desc = '220~240V,50~60Hz，4.6A';
Att1{
     7} = Equipment;
Equipment.FileName = 'YD8';
Equipment.Name = '饮水机';
Equipment.Desc = '220V,制热：430W，制冷：70W，总：500W';
Att1{
     8} = Equipment;
Equipment.FileName = 'YD9';
Equipment.Name = '挂式空调';
Equipment.Desc = '220V,2600W';
Att1{
     9} = Equipment;
Equipment.FileName = 'YD10';
Equipment.Name = '奔腾电吹风';
Equipment.Desc = '220V,50Hz,1400W';
Att1{
     10} = Equipment;
Equipment.FileName = 'YD11';
Equipment.Name = '创维电视';
Equipment.Desc = '220V,50Hz,150W';
Att1{
     11} = Equipment;
clear Equipment;

for i = 1:size(Att1,1)
Att1{
     i} = DataReader1(Att1{
     i},sheet1);
end

%读取附件 2 数据
Att2 = cell(2,1);
Att2{
     1}.FileName = '设备 1';
Att2{
     1}.Name = '设备 1';
Att2{
     1}.Desc = '';
Att2{
     2}.FileName = '设备 2';
Att2{
     2}.Name = '设备 2';
Att2{
     2}.Desc = '';
for i = 1:size(Att2,1)
Att2{
     i} = DataReader2(Att2{
     i},sheet2);
end

%读取附件 3 数据
Att3 = cell(6,1);
Att3{
     1}.FileName = '设备组 1-YD3+YD7';
Att3{
     1}.Name = ['设备组 1-',Att1{
     3}.Name,'+',Att1{
     7}.Name];
Att3{
     1}.Desc = '';
Att3{
     2}.FileName = '设备组 2-YD1+YD2+YD4';
Att3{
     2}.Name = ['设备组 2-',Att1{
     1}.Name,'+',Att1{
     2}.Name,'+',Att1{
     4}.Name];
Att3{
     2}.Desc = '';
Att3{
     3}.FileName = '设备组 3-YD4+YD5+YD8+YD10+YD11';
Att3{
     3}.Name = [' 设 备 组
3-',Att1{4}.Name,'+',Att1{5}.Name,'+',Att1{8}.Name,'+',Att1{10}.Name,'+',Att1{
     11}.Name];
Att3{
     3}.Desc = '';
Att3{
     4}.FileName = '设备组 4-YD2+YD8';
Att3{
     4}.Name = ['设备组 4-',Att1{
     2}.Name,'+',Att1{
     8}.Name];
Att3{
     4}.Desc = '';
Att3{
     5}.FileName = '设备组 5-YD3+YD5+YD11';
Att3{
     5}.Name = ['设备组 5-',Att1{
     3}.Name,'+',Att1{
     5}.Name,'+',Att1{
     11}.Name];
Att3{
     5}.Desc = '';
Att3{
     6}.FileName = '设备组 6-YD1+YD2+YD3+YD6+YD7';
Att3{
     6}.Name = [' 设 备 组
6-',Att1{1}.Name,'+',Att1{2}.Name,'+',Att1{3}.Name,'+',Att1{6}.Name,'+',Att1{
     7}.Name];
Att3{
     6}.Desc = '';

for i = 1:3
Att3{
     i} = DataReader1(Att3{
     i},sheet1);
end

for i = 4:6
Att3{
     i} = DataReader2(Att3{
     i},sheet2);
end

%读取附件 4 数据
Att4 = cell(3,1);
Att4{
     1}.FileName = '设备组 1';
Att4{
     1}.Name = '设备组 1';
Att4{
     1}.Desc = '';
Att4{
     2}.FileName = '设备组 2';
Att4{
     2}.Name = '设备组 2';
Att4{
     2}.Desc = '';
Att4{
     3}.FileName = '设备组 3';
Att4{
     3}.Name = '设备组 3';
Att4{
     3}.Desc = '';

for i = 1:size(Att4,1)
Att4{
     i} = DataReader2(Att4{
     i},sheet2);
end
save data.mat Att1 Att2 Att3 Att4
end
function Eq = DataReader1(Eq,sheet1)

% 读取四个表数据，并去除字段行和第一列
%设备数据
[~,~,SBSJ] = xlsread([Eq.FileName,'.xlsx'],sheet1{
     1});
SBSJ(1,:) = [];
TStr = SBSJ(:,1);
SBSJ(:,1) = [];
SBSJ = cell2mat(SBSJ);
%周波数据
[~,~,ZBSJ] = xlsread([Eq.FileName,'.xlsx'],sheet1{
     2});
ZBSJ(1,:) = [];
TStr1 = ZBSJ(:,1);
ZBSJ(:,1) = [];
ZBSJ = cell2mat(ZBSJ);
%谐波数据
[~,~,XBSJ] = xlsread([Eq.FileName,'.xlsx'],sheet1{
     3});
XBSJ(1,:) = [];
TStr2 = XBSJ(:,1);
XBSJ(:,1) = [];

XBSJ = cell2mat(XBSJ);
%操作记录
[~,~,CZJL] = xlsread([Eq.FileName,'.xlsx'],sheet1{
     4});
CZJL(1,:) = [];
Eq.t0 = datevec(TStr{
     1},'yyyy/mm/dd HH:MM:SS');%基准时间/起始时间

for i = 1:size(TStr,1)
str = TStr{
     i};%'March 28, 2012 11:51:00';
t = datevec(str,'yyyy/mm/dd HH:MM:SS');
Eq.Delay(i,1) = etime(t,Eq.t0);%时间戳
end

for i = 1:size(TStr1,1)
str = TStr1{
     i};%'March 28, 2012 11:51:00';
t = datevec(str,'yyyy/mm/dd HH:MM:SS');
Eq.Delay1(i,1) = etime(t,Eq.t0);%时间戳
end

for i = 1:size(TStr2,1)
str = TStr2{
     i};%'March 28, 2012 11:51:00';
t = datevec(str,'yyyy/mm/dd HH:MM:SS');
Eq.Delay2(i,1) = etime(t,Eq.t0);%时间戳
end

Eq.IC = SBSJ(:,1);%电流
Eq.UC = SBSJ(:,2);%电压
Eq.PC = SBSJ(:,3);%有功功率
Eq.QC = SBSJ(:,4);%无功功率
Eq.PFC = SBSJ(:,5);%功率因素
Eq.P = SBSJ(:,6);%总有功功率数据
Eq.Q = SBSJ(:,7);%总无功功率数据
Eq.PF = SBSJ(:,8);%总功率因素数据
%处理周波数据
ZBIC = ZBSJ(:,1:128);
ZBUC = ZBSJ(:,129:end);
idx = ZBIC>1000000;
ZBIC(idx) = ZBIC(idx) - 1666665;
idx = ZBUC>1000000;
ZBUC(idx) = ZBUC(idx) - 1666665;
Eq.ZBIC = ZBIC;
Eq.ZBUC = ZBUC;
%处理谐波数据
Eq.XBIC = XBSJ(:,2:21);
Eq.XBUC = XBSJ(:,52:71);
% 操作记录表
[SBMC,~,Idx] = unique(CZJL(:,3));
if size(SBMC,1)>1

for i = 1:size(SBMC,1)
CZJLtem = CZJL(Idx==i,:);
Eq.OP{
     i,1}.Name = SBMC{
     i};
opNum = size(CZJLtem,1);
ops = [];

for j = 2:opNum
str = CZJLtem{
     j,2};
t = datevec(str,'yyyy/mm/dd HH:MM:SS');
op.time = etime(t,Eq.t0);
op.workstate = CZJLtem{
     j,4};
op.oper = CZJLtem{
     j,5};
ops{
     j-1,1} = op;
op = [];
end

Eq.OP{
     i,1}.ops = ops;
end
else
opNum = size(CZJL,1);
ops = [];
for i = 2:opNum
str = CZJL{
     i,2};
t = datevec(str,'yyyy/mm/dd HH:MM:SS');
op.time = etime(t,Eq.t0);
% timeIdx = find(op.time == Eq.Delay);
% if isempty(timeIdx)
% else
% op.timeIdx = timeIdx;
% end
op.workstate = CZJL{
     i,4};
op.oper = CZJL{
     i,5};
ops{
     i-1,1} = op;
op = [];
end
Eq.OP = ops;
end
%计算实时用电量
edtime = Eq.Delay(end);
t = datetime(Eq.t0(1),Eq.t0(2),Eq.t0(3),Eq.t0(4),Eq.t0(5),Eq.t0(6):Eq.t0(6)+edtime);
t1 = datestr(t,'yyyy/mm/dd HH:MM:SS');
SSYDL.ID = cell(edtime+1,1);%实时用电量
for i = 1:size(SSYDL.ID,1)
SSYDL.ID{
     i} = Eq.FileName;
end
SSYDL.timestr = t1;
SSYDL.ydl(Eq.Delay+1,1) = Eq.UC .* Eq.IC / 36000000;%单位 W
idx = SSYDL.ydl == 0;
IBs = [];
j = 0;
k = 1;
while j < size(idx,1)
j = j+1;
if idx(j)
IBs{
     k,1}.st = j - 1;
while 1
j = j + 1;
if ~idx(j)
break;
end
end
IBs{
     k,1}.ed = j;
k = k + 1;
end
end
for j = 1:size(IBs,1)
st = IBs{
     j}.st;
ed = IBs{
     j}.ed;
ptnum = ed - st - 1;
delta = (SSYDL.ydl(ed) - SSYDL.ydl(st))/(ptnum+1);
for k = 1:ptnum
SSYDL.ydl(st+k) = SSYDL.ydl(st) + k*delta;
end
end
Eq.SSYDL = SSYDL;
end
function Eq = DataReader2(Eq,sheet2)
% 读取四个表数据，并去除字段行和第一列
%设备数据
[~,~,SBSJ] = xlsread([Eq.FileName,'.xlsx'],sheet2{
     1});
SBSJ(1,:) = [];
TStr = SBSJ(:,1);
SBSJ(:,1) = [];
SBSJ = cell2mat(SBSJ);
%周波数据
[~,~,ZBSJ] = xlsread([Eq.FileName,'.xlsx'],sheet2{
     2});
ZBSJ(1,:) = [];
TStr1 = ZBSJ(:,1);
ZBSJ(:,1) = [];

ZBSJ = cell2mat(ZBSJ);
%谐波数据
[~,~,XBSJ] = xlsread([Eq.FileName,'.xlsx'],sheet2{
     3});
XBSJ(1,:) = [];
TStr2 = XBSJ(:,1);
XBSJ(:,1) = [];
XBSJ = cell2mat(XBSJ);
Eq.t0 = datevec(TStr{
     1},'yyyy/mm/dd HH:MM:SS');%基准时间/起始时间
for i = 1:size(TStr,1)
str = TStr{
     i};%'March 28, 2012 11:51:00';
t = datevec(str,'yyyy/mm/dd HH:MM:SS');
Eq.Delay(i,1) = etime(t,Eq.t0);%时间戳
end
for i = 1:size(TStr1,1)
str = TStr1{
     i};%'March 28, 2012 11:51:00';
t = datevec(str,'yyyy/mm/dd HH:MM:SS');
Eq.Delay1(i,1) = etime(t,Eq.t0);%时间戳
end
for i = 1:size(TStr2,1)
str = TStr2{
     i};%'March 28, 2012 11:51:00';
t = datevec(str,'yyyy/mm/dd HH:MM:SS');
Eq.Delay2(i,1) = etime(t,Eq.t0);%时间戳
end
Eq.IC = SBSJ(:,1);%电流
Eq.UC = SBSJ(:,2);%电压
Eq.PC = SBSJ(:,3);%有功功率
Eq.QC = SBSJ(:,4);%无功功率
Eq.PFC = SBSJ(:,5);%功率因素
Eq.P = SBSJ(:,6);%总有功功率数据
Eq.Q = SBSJ(:,7);%总无功功率数据
Eq.PF = SBSJ(:,8);%总功率因素数据
%处理周波数据
ZBIC = ZBSJ(:,1:128);
ZBUC = ZBSJ(:,129:end);
idx = ZBIC>1000000;
ZBIC(idx) = ZBIC(idx) - 1666665;
idx = ZBUC>1000000;
ZBUC(idx) = ZBUC(idx) - 1666665;
Eq.ZBIC = ZBIC;
Eq.ZBUC = ZBUC;
%处理谐波数据
Eq.XBIC = XBSJ(:,2:21);
Eq.XBUC = XBSJ(:,52:71);

%计算实时用电量
edtime = Eq.Delay(end);
t = datetime(Eq.t0(1),Eq.t0(2),Eq.t0(3),Eq.t0(4),Eq.t0(5),Eq.t0(6):Eq.t0(6)+edtime);
t1 = datestr(t,'yyyy/mm/dd HH:MM:SS');
SSYDL.ID = cell(edtime+1,1);%实时用电量
for i = 1:size(SSYDL.ID,1)
SSYDL.ID{
     i} = Eq.FileName;
end
SSYDL.timestr = t1;
SSYDL.ydl(Eq.Delay+1,1) = Eq.UC .* Eq.IC / 36000000;%单位 W
idx = SSYDL.ydl == 0;
IBs = [];
j = 0;
k = 1;
while j < size(idx,1)
j = j+1;
if idx(j)
IBs{
     k,1}.st = j - 1;
while 1
j = j + 1;
if ~idx(j)
break;
end
end
IBs{
     k,1}.ed = j;
k = k + 1;
end
end
for j = 1:size(IBs,1)
st = IBs{
     j}.st;
ed = IBs{
     j}.ed;
ptnum = ed - st - 1;
delta = (SSYDL.ydl(ed) - SSYDL.ydl(st))/(ptnum+1);
for k = 1:ptnum
SSYDL.ydl(st+k) = SSYDL.ydl(st) + k*delta;
end
end
Eq.SSYDL = SSYDL;
end