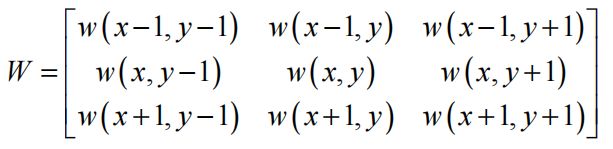“泰迪杯”挑战赛 - 通过数据挖掘技术实现道路缺陷自动识别

目 录

1. 挖掘目标
2. 分析方法与过程
   2.1. 总体流程
   2.2. 具体步骤
   2.2.1 缺陷图像预处理
   2.2.2 缺陷图像分割
   2.2.3 缺陷图像特征提取
   2.2.4 BP 神经网络模式识别
   2.3. 结果分析
3. 结论
4. 参考文献
5. 附 录

1. 挖掘目标

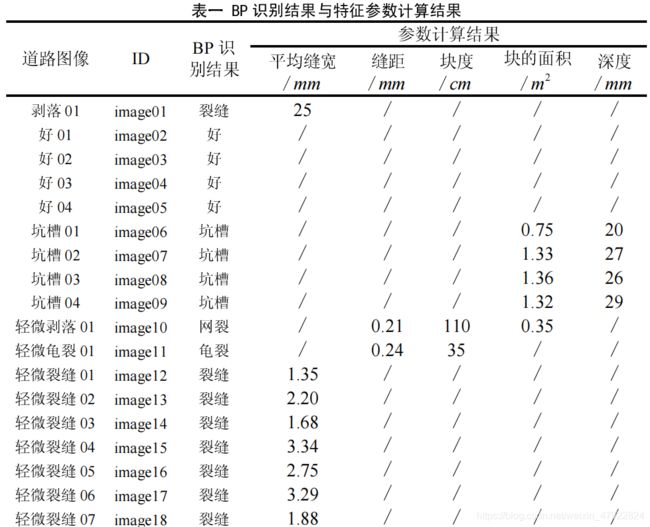
本次建模目标是利用附件所提供的道路缺陷图像，主要类型有：裂缝，龟裂，网裂，坑槽等缺陷。首先结合图形图像处理技术，对各类型图像进行特征提取和参数计算，并采用数据挖掘技术进行模式识别，以实现不同道路缺陷类别的自动识别。随着数字图像处理和模式识别技术的快速发展，不少研究人员开始试图利用图像识别技术来实现道路缺陷数据的调查研究。基于数字图像处理的道路路面病害自动识别技术可以及时掌握路面的破损情况，为路面的及时养护赢得时间的同时，也为养护资料的积累提供了方便，也充实了自动识别系统的数据库数据，从而为进一步制定道路养护规划决策提供科学依据。

2. 分析方法与过程

2.1. 总体流程

本次建模主要包括 3 个模块，分别是数据库查询模块、图像处理模块、参数计算模块。其中数据库查询模块主要实现从前端数据库读取缺陷图像，以及图像处理完成并且参数提取以后的参数统计等功能；图像处理模块主要实现图像灰度变换、图像去噪、图像分割等功能；参数计算模块主要实现对缺陷图像类型的判断，以及对线性裂缝长度的计算和网状裂缝的面积计算等功能，具体实现过程如图 1 所示。

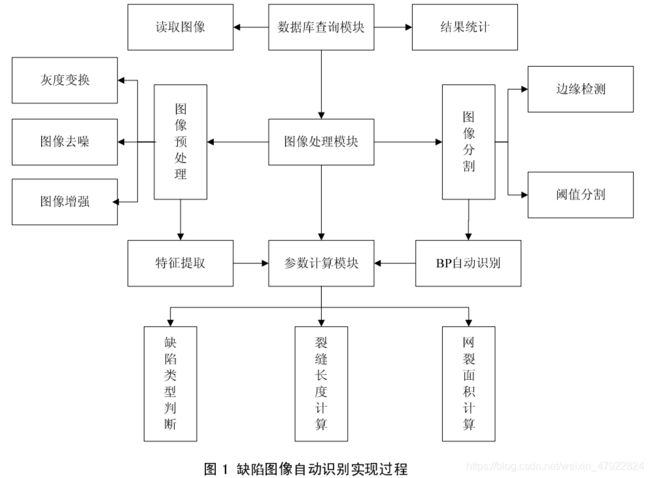
步骤一：利用 MATLAB 图形图像处理工具箱进行图像读取；
步骤二：编程进行图像处理模块的实现；
步骤三：对缺陷图像判断标准的参数进行计算并输出。
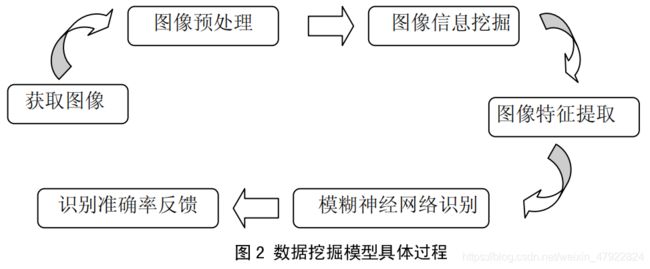
挖掘模型的具体流程如图 2 所示。

2.2. 具体步骤

2.2.1 缺陷图像预处理

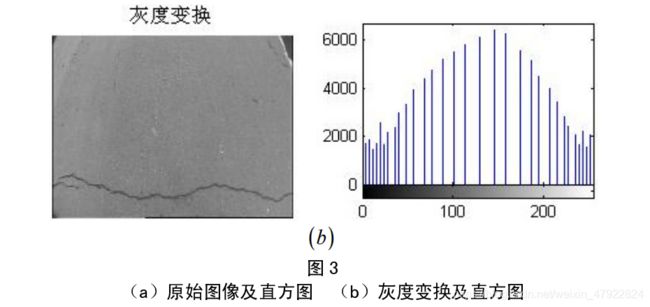
(1) 灰度变换
图像在形成、传输和记录的过程中，会由于成像系统、传输媒介和记录设备的不完善，使图像质量下降，形成退化图像，造成比较差的视觉效果和计算机处理上的困难。影响图像质量下降的因素包括成像系统和环境以及成像特点等，因此很难用一个显式的数学表达式来表征。

我们假设道路图像 $I(x,y)$ 由非均匀灰度(光照)的背景$I_b(x,y)$, 裂缝病害$I_n(x,y)$以
及石子、沥青等构成的噪声$I_c(x,y)$三部分相加组成，即
$$I(x,y)=I_b(x,y)+I_n(x,y)+I_c(x,y)$$

因此，如果可以找出背景信号，用原始图像减去背景就可以纠正灰度不均这一问题。从以上分析可以看出，关键在于背景图像的提取。在实际应用中，我们很难直接得到没有裂缝的背景，有时即使能得到，在时间轴上面的位置相距比较大，光照分布也往往不均匀。

经分析，我们考虑对背景子集双线性插值的方法来抽取拟合背景，算法步骤为：

Step 1 由原图像求取背景子集。对原图像分块，每块取一个背景点。光照不均在整幅图像表现明显，但在局部可以认为是近似均匀的。

Step 2 由子集做插值得到背景图像。由于图像的灰度变化是一个渐变的过程，考 虑利用双线性插值来对四个相邻的像素进行插值，因为这样产生的表面是连续的。


(2) 图像去噪

中值滤波是一种非线性处理技术，能抑制图像中的噪声，由于它在实际运算过程中并不需要图像的统计特性，所以使用比较方便。它是基于图像的这样一种特性：噪声往 往以孤立的点的形式出现，这些点对应的像素数很少，而图像则是由像素数较多、面积较大的小块构成。

中值滤波法虽然可以很好的去除图像中的孤立的噪声点，但是在抑制噪声的同时，也会对图像的边缘及细节有比较大的损害，使图像的边沿及细节变模糊。基于此，在本次挖掘建模中，提出一种梯度倒数加权平均滤波算法。

在一帧离散图像中，图像在一个区域内的灰度变化要比在区域之间的变化小，在边 缘处的梯度绝对值要比在区域内部的梯度绝对值高。在一个$n\times n$ 的窗口内，若把中心像素点与其各邻点之间的梯度绝对值的倒数定义为各邻点的加权值，则在区域内部的邻点，加权值最大；而在一条边缘附近的和位于区域外的邻点，加权值最小。这样对加权后的邻域进行局部平均，可使图像得到平滑，又不至于使边缘和细节明显模糊。为使平 滑后像素的灰度值在原图像的灰度范围内，应采用归一化的梯度倒数作为加权系数。具体实现算法如下：

设点( x, y) 的灰度值为 f( x, y) , n = 3。在它的3×3 的邻域内，定义梯度倒数为
$$g(x,y;i,j)=\frac{1}{|f(f(x+i,y+i)-f(x,y))|}$$

这里 i, j = -1,0,1，但 i 和 j 不能同时为 0 。计算(x,y)八个邻点的 g( x, y;i ,j ) 值，若 f(x+i,y+1)=f(x,y)，梯度为0 ，则定义 g( x,y; i,j ) 的范围在[0,2]之间，定义一个归一化的权重矩阵W 作为平滑的模板。其中，

规定中心元素 w(x,y ) ，其余八个加权元素之和为0.5，使得个元素总和等于1。于是有：
$$w(x+i,y+i)=\frac{1}{2}+\frac{g(x,y,i,j)}{{\sum }_i{\sum }_{j}g(x,y,i,j)}$$

其中，i ,j=-1,0,1 ，但i 和 j 不能同时为0 。

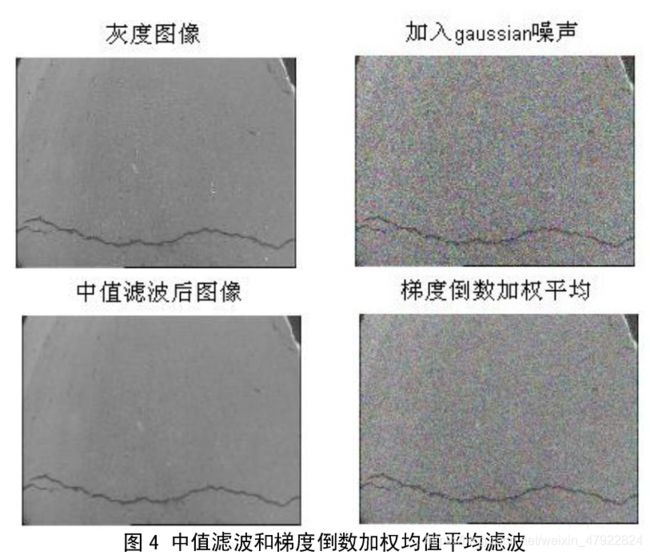
从图中可以看出，算法对图像噪声的滤除有一定效果，平滑了背景中的部分噪声， 一些细小的噪声已经被去除，大的噪声也有一定的减弱，并且保留了裂缝的边缘信息，在一定程度上有较好效果，尤其对裂缝和背景差别较大的图像效果会更明显。

(3) 图像增强

直方图是多种空间域处理技术的基础。直方图操作能够有效地应用于图像增强。灰度直方图的模型化处理，是指将图像的灰度值按照规定的灰度分布进行变换处理。这种变换方法适用于图像对比度较差、过于明亮或者过于黑暗，以及图像的灰度分布集中在明、暗两端的情况。直方图均衡化是其中一种非常有效的方法。也就是说，变换后的图像灰度值的分布是均匀的，所以图像的整体对比度得到了改善。应用数学公式来描述直方图均衡化如下：

$$g(x,y)=INT(\frac{v(u)-v_{min}}{1=v_{min}}(L-1))$$

其中， g( x, y) 为变换后图像的灰度值，u 为变换前图像的灰度值，v为灰度分布频度，$v_{min}$ 为灰度分布频度的最小值， INT 为取整。对图像严重裂缝 01.jpg，分别给出路面的原始直方图和均衡化后的直方图。

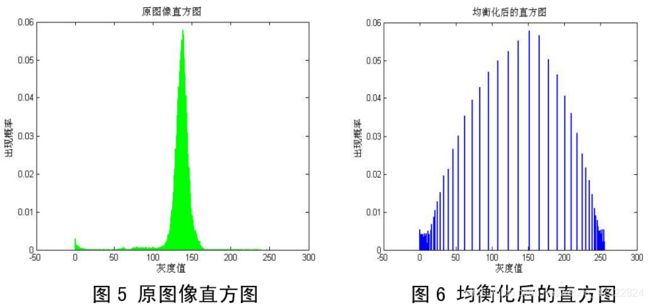
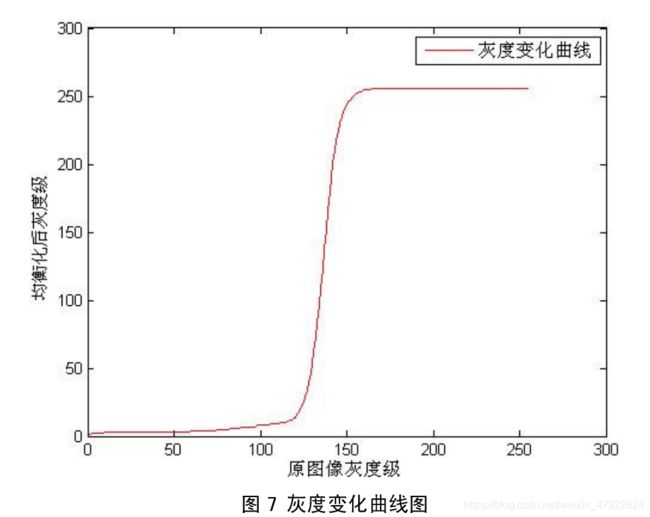
从均衡后之后裂缝图像的直方图可以看出，直方图的动态范围变大了，但与原始图
像直方图的“单峰”特性相比，直方图均衡化之后的图像的直方图的“单峰”特性不是
很明显。这是因为，图像的边缘在成像过程中曝光不均匀，造成图像增强以后直方图变
得有些“混乱”。

2.2.2 缺陷图像分割

(1) 边缘检测

图像边缘对图像识别和计算机分析十分有用。边缘能够勾划出目标物体，使观察者一目了然；边缘蕴含了丰富的内在信息，是图像识别中重要的图像特征之一。从本质上，图像边缘是图像局部特性不连续的反映，它标志着一个区域的终结和另一个区域的开始。

由于路面裂缝灰度变化更大，可以采用边缘检测的方法，对路面裂缝进行识别。对于路面裂缝检测来说，边缘检测算法在很大程度上影响着识别和检测的效果与精度。最简单的边缘检测方法是对原始图像按像素的某领域构造边缘检测算子。目前，提取边缘常用的方法主要包括：模版匹配法、曲面拟合法、边缘算子法等。

边缘检测的实质是采用某种算法来提取出图像中对象与背景间的交界线。我们将边缘定义为图像中灰度发生急剧变化的区域边界。图像灰度的变化情况可以用图像灰度分布的梯度来反映，因此我们可以用局部图像微分技术来获得边缘检测算子。经典的边缘检测方法，是对原始图像中像素的某小邻域来构造边缘检测算子。

若记，$▽f(x,y)=\frac{\delta f}{\delta x}i+\frac{\delta f}{\delta y}j$为图像的梯度，$\delta f(x,y)$ 包含灰度变化信息，设$e(x,y)+\sqrt{f_x^2+f_y^2}$为$f(x,y)$的梯度，e (x, y) 可以用作边缘检测算子。为了简化计算，也可以将 e( x,y ) 定义为偏导数 $f_x$ 与 $f_y$ 的绝对值之和：

$$e(x,y)+|f_x(x,y)|+|f_y(x,y)|$$

以这些理论为依据，提出了许多算法，常用的边缘检测方法有： Roberts 边缘检测算子、Sobel 边缘检测算子、Prewitt 边缘检测算子、Canny 边缘检测算子、Laplace边缘检测算子等。

从图中可以看出，Roberts算子提取边缘的结果边缘较粗，边缘定位不很准确，Sobel算子和Prewitt 算子对边缘的定位就准确了一些，而采用拉普拉斯高斯算子进行边缘提取的结果要明显优于前三种算子，特别是边缘比较完整，位置比较准确。相比而言，Canny算子提取的边缘最为完整，而且边缘的连续性很好，效果优于以上其他算子，这主要是因为它进行了“非极大值抑制”和形态学连接操作的结果。

上面几种基于微分的经典边缘提取算子，它们共同的优点是计算简单、速度较快，缺点是对噪声的干扰都比较敏感。在实际应用中，由于图像噪声的影响，总要将经典的 算法进行改善结合其他一些算法对一幅含噪声的图像进行处理，然后再采用经典的边缘提取算子提取图像边缘。

(2) 阈值分割
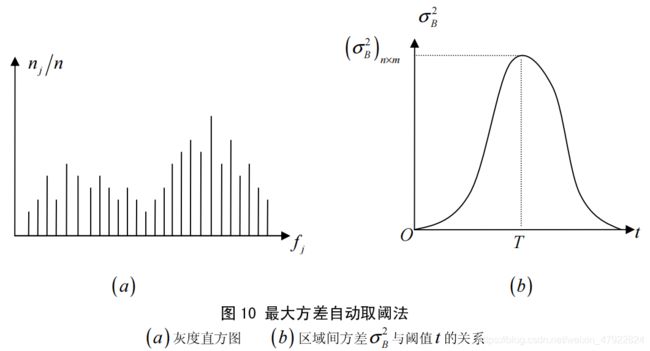
图像灰度直方图的形状是多变的，有双峰但无明显低谷或者是双峰与低谷都不明显，而且两个区域的面积比也难以确定的情况经常出现，采用最大方差自动取阈法往往能够得到较满意的结果。

图 10 (a)为包含有两类区域的图像的灰度直方图，设t 为分离两个区域的阈值。由直方图经过统计可以得到被t 分离后的区域 A 、区域 B 占整个图像的面积比以及整幅图像、区域 A、区域 B 的平均灰度为

$$区域A面积比{\delta }_1=\sum _{j=0}^t\frac{n_j}{n}$$
$$区域B面积比{\delta }_2=\sum _{j=t+1}^{G-1}\frac{n_j}{n}$$

或者

$$整幅图像的平均灰度\delta =\sum _{j=0}^{G-1}(f_j\times \frac{n_j}{n})$$
$$区域A的平均灰度\delta =\frac{1}{{\delta }_1}\sum _{j=0}^t(f_j\times \frac{n_j}{n})$$
$$区域B的平均灰度\delta =\frac{1}{{\delta }_2}\sum _{j=t+1}^t(f_j\times \frac{n_j}{n})$$

式中，G 为图像的灰度级数。

中，G 为图像的灰度级数。
由此，可以得到整幅图像平均灰度与区域 A、区域 B 平均灰度值之间的关系为
$$\mu ={\mu }_1{\delta }_1+{\mu }_2{\delta }_2$$

同一区域常常具有灰度相似特性，而不同区域之间则表现为明显的灰度差异，当被阈值
t 分离的两个区域间灰度差异较大时，两个区域的平均灰度${\mu }_1{\mu }_2$与整图像平均灰度 $\mu$之
差也较大，区域间的方差就是描述这种差异的有效参数，其表达式为
$${\sigma }_B^2={\delta }_1({\mu }_1-\mu {)}^2+{\delta }_2(t)({\mu }_2(t)-\mu {)}^2$$

其中，${\sigma }_B^2$表示图像被阈值t 分割后两个区域之间的方差。显然，不同的阈值t ，就会得到不同的阈值间方差，也就是说，区域间方差、区域 A均值、区域 B 均值、区域 A面积比、区域 B 面积比都是阈值t 的函数，因此，可以得到下式
$${\sigma }_B^2={\delta }_1[({\mu }_1(t)-\mu {)}^2]+{\delta }_2(t)[({\mu }_2(t)-\mu {]}^2$$

显然，被分割的两个区域间方差达到最大时，被认为是两个区域的最佳分离状态，由此确定阈值T (如图 10(b) )
$$T=Max\{{\sigma }_B^2(t)\}$$

以最大方差决定阈值不需要认为设定其他参数，是一种自动选择阈值的方法，它不仅适用于两个区域的单阈值选择，也可扩展到多区域的多阈值选择中去。

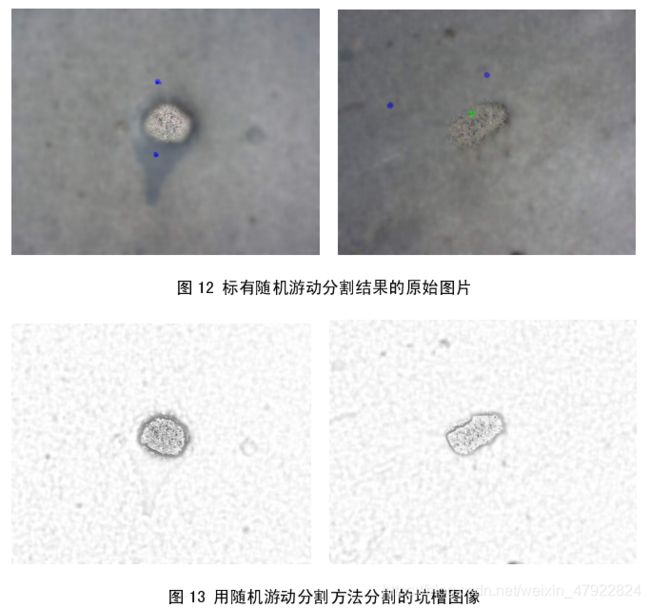
(3) 基于随机游动方法的道路缺陷图像分割

随机游动的前提是游动前需要确定种子点，来确定随机游动的终点，否则只能无止境地游动而不能被吸收。但是由于路面图像的数量较多，需要分析大量的图片才能知道路面的损坏情况，所以采用人工交互的方式确定种子点的方法是不可行的，这就要求通过分析图像自动确定种子点的位置。针对道路坑槽的区域性特点，提出如下算法：

因为最终图像将被分割成背景和目标，所以需要两类种子点分别代表目标和背景。

通过仔细分析路面坑槽的图像可以知道，坑槽属于块状病害，它在图像中的特点是：病害成块出现，形成一个不同于路面背景的区域。这就决定了坑槽区域的像素值区别于其他区域的像素值，并且坑槽内部像素分布均匀。根据这一特点，首先对路面图像采用了分块的方法得到路面图像的特征子图，再对特征子图采用投影法来确定坑槽的大致位置，找到目标内的种子点。

具体做法是：

首先根据不均匀图像中包含的信息比较多，比如目标与背景分界处的图像块，而评价某区域信息是否丰富的简单合理依据是判断方差是否足够大，并且坑槽的边缘基本是连续的，这样就使得图像的特征子图在 x 方向和 y 方向上方差较大的值集中在一个区域，基于此，我们在 x 和 y 方向上分别对坑槽特征子图做投影，取每行和每列的最大值。

由于坑槽的边缘出现较大的灰度变化，那么所在子块的方差较大，所以方差较大的点是我们重点研究的对象。但是，我们需要去掉离群点，才能比较容易地确定坑槽的大 体位置。

从图像分割结果可以看出来，在图像质量不高，噪声影响较大的情况下，随机游动可以清晰地分出路面坑槽图像，随机游动的方法在分割路面图像中体现了其优越性。

目前，在图像特征提取方面已经有了很成熟的理论如纹理特征、几何特征、统计特征，并且现在还不断地有新的理论在产生，例如，数学形态特征、分形特征、投影特征、 三维特征等。路面裂缝特征的提取主要包括缺陷类型的判断以及平均缝宽、长度、面积的计算等。如何快速、准确地提取出这些参数，是研究的一个重点，也是一个难点。

(1) 裂缝类型的初级判断

裂缝类型主要分为网状裂缝、块状裂缝、横向裂缝和纵向裂缝。为研究的方便，本文将网状裂缝和块状裂缝划分为网状裂缝，将横向裂缝和纵向裂缝划分为线性裂缝。常用的裂缝判别方法主要是投影法，但是该方法对于网状裂缝的判断误差较大，所以本文采用一种阈值判定的方法，有效地减小了类型判断的误差。

本文判别路面裂缝类型的步骤：
Step 1 根据设定阈值判断裂缝为网裂还是线性裂缝；
Step 2 若是网裂，则根据块度判断是轻微网裂还是严重网裂；若不是网裂，则进 行 Step 3；
Step 3 根据投影判别法判断裂缝是纵向裂缝还是横向裂缝，并根据平均缝宽识别其是轻微裂缝还是严重裂缝。

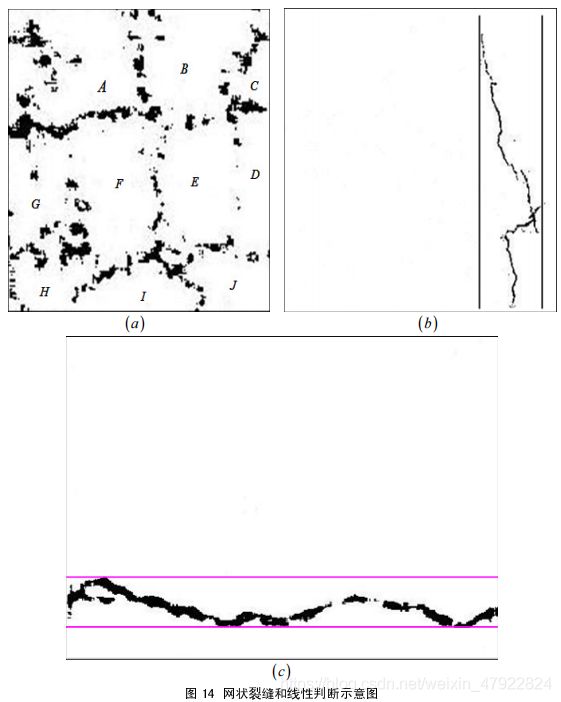
对于路面裂缝类型的判断，首先设定一个阈值，然后计算像素点为0 的连通区域个数，根据求得的连通区域个数与设定的阈值进行比较，若连通区域个数大于该阈值，则判定该裂缝图像为网状裂缝，否则，判定该裂缝为线性裂缝。

由于路面裂缝图像一般噪音点很多，结合多次试验结果，设定初试阈值为 20 。如图14(a)，图像(a)是网裂类型的一部分。经过分析，我们得到连通区域个数大于阈值20 ，由此判断此裂缝为网状裂缝。否则若小于该阈值，则判定为线性裂缝，如图 ( ) ( ) 14 , b c 。

根据实际需要，还需对线性裂缝进一步判别，判断出横向裂缝以及纵向裂缝。下面讨论这两种裂缝的判别方法。

对于横向裂缝、纵向裂缝的判别，可以对裂缝图像分别向 x 轴， y 轴投影，然后分别计算两个方向上投影的长度并进行对比分析，如果 x 轴像素投影长度大于 y 轴像素投影长度，则说明裂缝沿 x 轴方向长度大于沿 y 轴方向长度，可判定该裂缝图像为横向裂缝，反之，对于沿 y 轴像素投影长度大于沿 x 轴像素投影长度的，可以判定为纵向裂缝，如图 14 (b) © 。

图15给出了坑槽缺陷图像在各个方向上的灰度投影，从图中可以看出，蓝色、绿色、红色曲线已经明显分离。

(2) 面积的计算过程

根据坑槽路面破损图像子块特征值的识别结果，通过搜索法确定待测量坑槽的边 缘。首先将坑槽子块图像特征值矩阵四周扩充各一行或一列，设定扩充值全部为0 。搜 索扩充后的路面破损子块特征值矩阵各行或各列，如果其中一行或一列不全部为0 而其外部的各行各列却全部为0 ，则此行或列即为路面破损子块特征值的边缘。接着，对由坑槽边缘所组成的长方形中的子块图像进行计数。最后进行坑槽面积的计算。

设 S 为待测量的坑槽面积，N 为长方形内子块图像的个数，a 为单个路面子块图像所对应的实际面积。则 S=Na 。

网裂为一系列相互交叉连接的裂缝，将道路分为块度较小的裂块。通常缝距为0.2~0.3m ，块的面积为0.1 ~ 10m2。由于面积较大，因此，对于网裂的道路，整幅道路缺陷图像所包含的面积都属于破损面积，即网裂的破损面积为：$S=(x_2-x_1)(y_2-y_1)$。

(3) 平均缝宽的计算过程
在公路路基路面现场测试规程《JTJ095-95》中规定：裂缝块度是评价单根裂缝的破损程度的主要评价依据。因此，有必要对单根裂缝的平均宽度进行测量。道路缺陷图像测量过程需要经过预处理、二值化、测量等步骤。

假设，二值化后裂缝子块图像中裂缝区域的像素沿着水平方向或纵轴方向投影计数值为$t_i$，每个像素代表的实际路面宽度为 w，则裂缝宽度 L 为
$$L=\frac{{\sum }_{i=1}^n{t}_i}{n}w$$

记单根裂缝的面积为$S_{sig}$,则
$$S_{sig}=L\times 0.2(m)=\frac{{\sum }_{i=1}^n{t}_i}{n}w\times 0.2(m)$$

(4) 路面破损块度的计算

块度(Blockness Size) 是矿石、岩石经爆破、破碎后形成碎块的大小程度。其一般以 碎片的三向长度的平均值或碎块的最大长度表示。为方便计算，本文采取后一种计算方法，即道路分成块的最大直径。缝距，是指裂缝之间的最小距离。块度和缝距是区别“龟 裂”和“网裂”的度量标准。

2.2.4 BP 神经网络模式识别

由于路面缺陷子块图像特征值分布没有明显的规律，采用线性分类器难以实现路面缺陷子块图像的正确分类，因此我们选用BP 神经网络分类器。

测量路面破损，首先应对路面图像进行二值化等图像处理，以确定路面破损边缘。由于路面图像内容复杂，加之受光照、路面噪声等因素的干扰，依据路面破损图像的全局直方图特征进行路面破损识别存在着较大的难度。因此，我们对复杂图像进行分割的处理方法，即将整幅路面图像分块，提取子块图像的灰度方差作为特征值，并设计分类器进行子块图像模式的识别。

(1) 路面缺陷子块图像划分

将图15所示的路面图像等分为32 32 × 像素的子块图像，并计算出各个子块图像灰度标准差矩阵如图16所示。从图中，我们发现，连线部分标准差值与图片中的裂纹部分基本对应。如果子块图像灰度标准差越大，则该子块路面破损越严重。因此，采用分块处理路面缺陷图像特征分析的方法较为合理。

(2) 路面缺陷子块图像特征值的选取

根据前文介绍，我们采用选取子块路面图像原始灰度值的直方图特征作为子块路面图像特征。常用的直方图统计信息如下：
灰度均值：$\mu ={\sum }_{i=0}^{L-1}i\times p(i)$
灰度方差：$\eta ={\sigma }^2{\sum }_{i=0}^{L-1}(i-\mu {)}^2\times p(i)$
扭曲度：$S=\frac{1}{{\sigma }^3}{\sum }_{i=0}^{L-1}(i-\mu {)}^3\times p(i)$
峰度：$Energy={\sum }_{i=0}^{L-1}(p(i){)}^2$
熵：$Entropy=-{\sum }_{i=0}^{L-1}p(i)\times logp(i)$

其中， L 为量化层数，即灰度级数，这里 L = 256； p(i)为灰度级i 的概率。

在这里，灰度方差是灰度分布的分散性的度量；扭曲度（又称偏度）是对分布偏离对称情况的度量；峰度是描述一个分布的倾向是聚集于均值附近还是散布于两端的度量；而对于等概率的分布则具有最小的能量而同时又具有最大的熵。

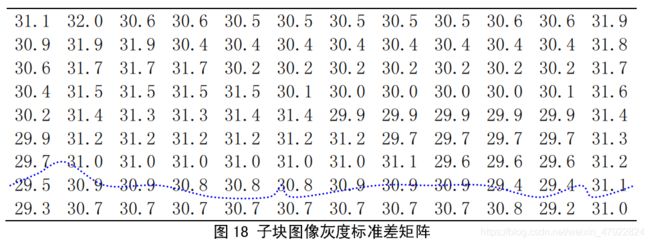
从图18可以看出，子块图像灰度标准差矩阵基本可以表征路面破损图像特征，而有灰度方差${\sigma }^2$ 的计算方法，可知用子块图像方差值作为特征值会加大不同类别的子块图像灰度特征值之间的差别，因此，选择子块图像灰度方差作为图像特征值。

(3) 路面缺陷子块图像的模式识别

Step 1 我们把路面子块图像的模式分为：好的路面子块图像模式，用0 表示；路面破损子块图像，用1表示。

Step 2 分类器输入值的确定

由前面的分析知道，对于不同路面图像的子块图像，只根据灰度方差${\eta }_j$，并不能很好地判别子块图像模式，即使两幅代表不同的路面的子块图像模式，但子块图像的灰度方差可能相同。由于同一张路面图像中所有子块图像的灰度方差均值$\overline{{\eta }_j}$，能够反映同一幅路面图像的总体信息；同一幅路面图像中所有子块图像灰度方差的最小值$({\eta }_j{)}_{min}$，能够反映出同一幅路面图像中破损程度最小的子块图像信息。因此，选用向量$I_j=[\eta ,\overline{{\eta }_j},({\eta }_j{)}_{min}]$, 作为分类器的输入值。

Step 3 分类器训练与子块图像模式识别

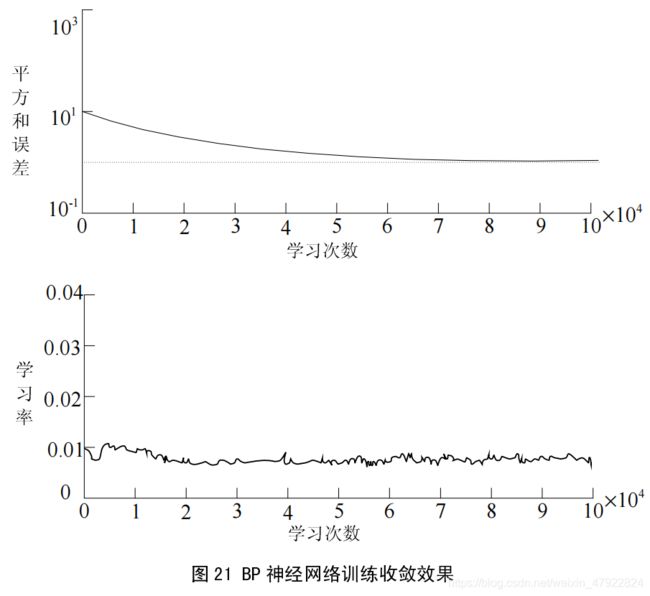
本文选用的BP 网络分类器采用1个隐层，输入层为3个，输出层节点为1个。经过试算，隐层选用9个节点。

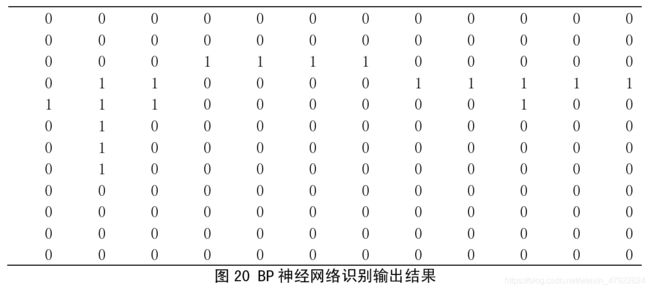
采用250 个路面子块图像的样本对BP 网络进行训练，若目标误差设定为0.015，则经过100000次训练后学习过程收敛。BP 网络训练成功后，对图19所示的路面图像的子块图像模式进行识别实验。在判断结果时，网络实际输入值大于0.5取整为1，小于0.5取 整为0 ，结果见图18。对两幅图对比分析，可以看出路面破损区域所在的位置与图20 中 1的位置基本吻合。实验表明，采用神经网络分类器可较好地识别路面破损子块图像模式。

2.3. 结果分析

本文首先介绍数字图像处理技术，然后利用图像预处理方法，对路面裂缝图像首先进行了灰度化处理；对处理后的灰度图像进行去噪处理，包括图像平滑，如中值滤波、均值滤波等；然后根据路面图像中的裂缝模糊不清晰的情况，进行了图像增强处理。在图像分割部分，首先介绍基于边缘检测的方法，比较分析了几种常用的边缘检测算法。然后介绍了灰度阈值分割方法，并将裂缝从背景中较好地得到分离。最后对二值图像进行细化，得到单像素的裂缝，为后续裂缝的长度、缝宽和面积的计算打下了基础。
对经过预处理和阈值分割后的裂缝首先进行了类型判断，归类出网状裂缝、纵向裂缝以及横向裂缝。然后介绍网状裂缝外接矩的面积计算方法，以及横向和纵向长度的计算方法。通过对采集来的图像进行实验测试，表明该方法是可行和有效的，并且实验效果可以达到后续道路养护施工的要求。

3. 结论

随着我国经济的快速发展，公路的建设也取得了巨大成就，同时，随着我国道路网络体系的日趋完善，为了提高公路使用寿命，公路的养护工作就变得越来越重要，仅仅依靠传统的人工检测公路破损情况的方法已经不能适应公路的发展需要了，因此，公路路面破损的自动检测和识别系统的研究与开发就显得极为迫切，是目前在模式识别领域研究的热点和难点。

本次数据挖掘建模的目标是根据所采集到的道路缺陷图像，包括裂缝、网裂、龟裂、坑槽四种类型，运用图像处理技术，对不同道路缺陷类别进行特征提取，并采用数据挖掘技术进行模式识别，最终实现缺陷类型的自动识别。在建模过程中，我们运用 MATLAB的图像处理工具箱，进行道路缺陷图像的预处理、图像分割等研究，特别地，我们提出了随机游动分割算法对坑槽图像进行图像分割，与其他分割方法相比，此算法具有分割背景清晰、快速的特点，以及各类评价参数的计算，通过实验，可以看出，基于BP 神经网络的道路缺陷图像的模式识别具有较高的识别准确率和识别效率。

通过本次建模的研究，希望能为政府工作人员提供较为合理的理论支撑和科学依据，为我国的道路养护工作的发展做出应有的贡献。

4. 参考文献

[1] 张全升，荆根强，杨峰.高速公路路面破损与路基病害三维一体化检测技术研究[J].公路交通科技(应用技术版)，2006-09：37-41

[2] 王士清，韩力群.用于公路路面状况自动检测的图像处理技术[J].科技情报开发与经济，2003，13(8)：167-168

[3] 魏丹，陈淑珍，陈彬等.梯度倒数加权平滑算法的改进与实现[J].计算机应用研究，2005，3：153-154

[4] 周伟，王承训.焊接缺陷自动识别系统的研究和应用[J].焊接学报，1992,13(1)：45-50

[5] 赵珂.路面裂缝图像自动识别系统研究[J].长安大学硕士学位论文，2009

[6] 刑荣军.高速公路路面破损自动识别与智能评价[J].重庆交通大学硕士学位论文，2011

[7] 初秀民，王荣本，储江伟，王超.沥青路面破损图像分割方法研究[J].中国公路学报，2003,16(3)：11-14

[8] 蒋彬，刘淑荣.基于图像识别的公路路面破损自动检测研究进展[J].东北公路，2002,25(3)：19-21

[9] 胡曦.路面病害自动检测技术研究与系统实现[J].南京理工大学硕士学位论文，2003

[10] 王晓明，冯鑫，党建武.路面病害检测中的背景处理和断点连接算法[J].兰州理工大学学报，2012,38(4)：63-67

[11] 马旭.种子法特征图像提取实例及其 MATLAB 实现[J].计算机与数字工程，2010,38(12)：116-120

[12] 杨劲夫.高速公路车辙检测数据分析方法[J].东北公路，2002,25(1)：8-9

[13] 付海燕.基于纹理分析的板带材表面缺陷分类与检测识别方法研究[J].东北大学硕士学位论文，2004

[14] 甄庆龙.沥青混凝土路面缺陷的检测方法[J].长春：中国电子商务，2010.11

5. 附 录

%%===================================================================%% 
reci_gradu_weighted.m 
a=imread('image26.jpg'); 
figure(1); 
subplot(221) 
imshow(a); 
title('原始图像') 
a=imnoise(a,'gaussian',0.005); 
subplot(222); 
imshow(a); 
title('加入gaussian噪声') 
a=double(a); 
[dep,wide]=size(a); 
new_image=ones(size(a)); 
 
r=0.5; 
for i=2:dep-1 
 for j=2:wide-1 
 g=0; 
 for m=-1:1 
 for n=-1:1 
 if(a(i+m,j+n)-a(i,j)==0) 
 g(m+2,n+2)=0; 
 else 
 g(m+2,n+2)=1/abs(a(i+m,j+n)-a(i,j)); 
 end 
 end 
 end 
 
 G=sum(sum(g)); 
 for m=-1:1 
 for n=-1:1 
 w(m+2,n+2)=g(m+2,n+2)/G; 
 end 
 end 
 
 
new_image(i,j)=a(i,j)*r+(w(-1+2,-1+2)*a(i-1,j-1)+w(-1+2,0+2)*... 
 
a(i-1,j)+w(-1+2,1+2)*a(i-1,j+1)+w(0+2,-1+2)*a(i,j-1)+w(0+2,1+2)*... 
 
a(i,j+1)+w(1+2,-1+2)*a(i+1,j-1)+w(1+2,0+2)*a(i+1,j)+w(1+2,1+2)*... 
 a(i+1,j+1))*(1-r); 
 
 end 
end 
 
for i=2:dep-1 
 new_image(i,1)=new_image(i,2); 
 new_image(i,wide)=new_image(i,wide-1); 
end 
 
new_image(1,:)=new_image(2,:);
new_image(dep,:)=new_image(dep-1,:); 
 
 
 subplot(223); 
 imshow(uint8(a)) 
 title('梯度加权') 
 subplot(224) 
 imshow(uint8(new_image)) 
 title('梯度倒数加权平均') 
 %%===================================================================
%% 
%%===================================================================%% 
FCM.m 
clear all 
I0=imread('image09.jpg');%读入图像文件
I=rgb2gray(I0);%转换为灰度图像
figure(1); 
imshow(I); 
title('原始图像'); %显示原来的图像
count=imhist(I); %灰度频率
[m,n]=size(I); %测矩阵的大小
h=count/(m*n) %求灰度级数
V1=zeros(2); %确定对称矩阵A 
V2=zeros(2); 
U1=zeros(2,256); %设定分区矩阵U 
m1=2; %确定加权指数m 
V1(1)=20; %初始化聚类中心V，C=2 
V1(2)=250; 
l=length(h) 
I=double(I);%转换变量的类型
diedai=1; 
while (diedai==1) 
 for i=1:l %修改迭代过程中的分区矩阵
 if (i-V1(1))^2>0.01&(i-V1(2))^2>0.01 
 tep1=(i-V1(1))^2; 
 tep2=(i-V1(2))^2; 
 U1(1,i)=1.0/(1+(tep1/tep2)^(1.0/(m1-1))); 
 U1(2,i)=1.0/(1+(tep2/tep1)^(1.0/(m1-1))); 
 else 
 if (i-V1(1))^2<0.01 
 U1(1,i)=1.0; 
 else 
 U1(2,i)=0.0; 
 end 
 if (i-V1(2))^2<0.01 
 U1(1,i)=0.0; 
 else 
 U1(2,i)=1.0; 
 end 
 end 
 end 
 tep1=0.0; 
 tep2=0.0; 
 tep3=0.0; 
 tep4=0.0;
for i=1:l %求迭代过程中的聚类中心
 tep1=tep1+h(i)*(i)*U1(1,i)^m1; 
 tep2=tep2+h(i)*U1(1,i)^m1; 
 tep3=tep3+h(i)*(i)*U1(2,i)^m1; 
 tep4=tep4+h(i)*U1(2,i)^m1; 
 end 
 V2(1)=tep1/tep2; 
 V2(2)=tep3/tep4; 
 if (V1(1)-V2(1))^2<0.01&(V1(2)-V2(2))^2<0.01 
 diedai=0; %迭代停止判断，阈值取0.01 
 else 
 V1(1)=V2(1); 
 V1(2)=V2(2); 
 end 
end 
 
I1=zeros(m,n); % m,n为图像的尺度
for i=1:m %二值化图像
 for j=1:n 
 if (I(i,j)-V2(1))^2>(I(i,j)-V2(2))^2 % 距离聚类中心近，则将二值图数值置% 为1，否则，置为0 
 I1(i,j)=250; 
 else I1(i,j)=0; 
 end 
 end 
end 
figure(2); 
I1=uint8(I1); % 转换为无符号型整数，8表示8位二进制整数，范围0~255 
imshow(I1);title('分割后的图像'); %显示分割后的图
%%===================================================================%% 
%%===================================================================%% 
Medfilter.m 
clc; 
clear all; 
img=imread('image26.jpg'); 
img_0=rgb2gray(img); 
img_1=imnoise(img_0,'salt & pepper',0.02); 
img_2=medfilt2(img_1); 
subplot(2,2,1);imshow(img);title('原始图像'); 
subplot(2,2,2);imshow(img_0);title('灰度图像'); 
subplot(2,2,3);imshow(img_1);title('加入噪声后图像'); 
subplot(2,2,4);imshow(img_2);title('中值滤波后图像'); 
%%===================================================================%% 
%%===================================================================%% 
findwhite.m 
%% step 1 
clear all 
clc 
I=imread('image26.jpg');%读入图像
bwI=im2bw(I,0.5);%转化为二值图像
bwI 
L=bwlabel(bwI,4);%将四连通区域进行标记
[r,c]=find(L==1); 
%查找其中的白色区域，r是白点所在行组成的向量，c是白点所在的列组成的向量
[r,c] 
%% step 2 %去除r中重复的数
new_r=[]; 
for i=1:length(r) 
 nn=find(new_r==r(i)); 
 if isempty(nn),new_r=[new_r r(i)];end 
end 
%% step 3 
sum_zeros=0;%轮廓中总的点个数
for i=1:length(new_r) 
 n=find(bwI(new_r(i),:)==1);%查找有白点的行中白点所在的位置
 if length(n)==1,continue;end%如果该行中只有一个白点，则返回
 num_zeros=n(end)-n(1)+1-length(n);%否则计算夹在白点之间的黑点的个数
 sum_zeros=sum_zeros+num_zeros; 
end 
%%===================================================================%% 
%%===================================================================%% 
rangefilt.m 
I = imread('image24.jpg');%读取图像
figure; imshow(I);%显示原图像
E = entropyfilt(I);%创建纹理图像
Eim = mat2gray(E);%转化为灰度图像
figure; subplot(121) 
imshow(Eim);%显示灰度图像
BW1 = im2bw(Eim, .8);%转化为二值图像
subplot(122); imshow(BW1);%显示二值图像
BWao = bwareaopen(BW1,2000);%提取底部纹理
figure; subplot(121) 
imshow(BWao);%显示底部纹理图像
nhood = true(9); 
closeBWao = imclose(BWao,nhood);%形态学关操作
subplot(122); imshow(closeBWao)%显示边缘光滑后的图像
roughMask = imfill(closeBWao,'holes');%填充操作
figure; subplot(121) 
imshow(roughMask);%显示填充后的图像
I2 = I; 
I2(roughMask) = 0;%底部置为黑色
subplot(122); imshow(I2);%突出显示图像的顶部
E2 = entropyfilt(I2);%创建纹理图像
E2im = mat2gray(E2);%转化为灰度图像
figure; subplot(121) 
imshow(E2im);%显示纹理图像
BW2 = im2bw(E2im,graythresh(E2im));%转化为二值图像
subplot(122); imshow(BW2)%显示二值图像
mask2 = bwareaopen(BW2,1000);%求取图像顶部的纹理掩膜
figure; imshow(mask2);%显示顶部纹理掩膜图像
texture1 = I; texture1(~mask2) = 0;%底部置为黑色
texture2 = I; texture2(mask2) = 0;%顶部置为黑色
figure; subplot(121)%显示图像顶部

imshow(texture1); subplot(122), 
imshow(texture2);%显示图像底部
boundary = bwperim(mask2);%求取边界
segmentResults = I; 
segmentResults(boundary) = 255;%边界处设置为白色
figure; imshow(segmentResults);%显示分割结果
S = stdfilt(I,nhood);%标准差滤波
figure; subplot(121) 
imshow(mat2gray(S));%显示标准差滤波后的图像
R = rangefilt(I,ones(5));%rangefilt滤波
subplot(122); imshow(R);%显示rangefilt滤波后的图像
%%===================================================================%% 
%%===================================================================%% 
edgetest.m 
I = imread('image26.jpg');%读取图像
figure; imshow(I);%显示原图像
Eim=rgb2gray(I);%转化为灰度图像
im1=edge(Eim,'roberts');%使用 roberts 方法检测边缘
im2=edge(Eim,'sobel');%使用 sobel 方法检测边缘
im3=edge(Eim,'prewitt');%使用 prewitt 方法检测边缘
im4=edge(Eim,'log');%使用 log 方法检测边缘
im5=edge(Eim, 'canny');%使用 canny 方法检测边缘
subplot(331), imshow(Eim);title('灰度图像');%显示灰度图像
subplot(332), imshow(im1);title('Roberts 方法检测'); 
%显示 roberts 方法检测的边缘
subplot(333), imshow(im2);title('Sobel 方法检测'); 
%显示 sobel 方法检测的边缘
subplot(334), imshow(im2);title('Prewitt 方法检测'); 
%显示 prewitt 方法检测的边缘
subplot(335), imshow(im4);title('Log 方法检测');%显示 log 方法检测的边缘
subplot(336), imshow(im5);title('Canny 方法检测'); 
%显示 canny 方法检测的边缘
%%===================================================================%% 
%%===================================================================%% 
Cutandsave.m 
%得到图片，并将图片分成相等的区域，然后得到每个区域分别保存：
I=imread('image26.jpg'); 
Im=rgb2gray(I); 
imshow(Im) 
hold on 
L = size(Im); 
height=32; 
width=32; 
max_row = floor(L(1)/height); 
max_col = floor(L(2)/width); 
seg = cell(max_row,max_col); 
%分块
for row = 1:max_row 
 for col = 1:max_col 
 seg(row,col)=
  end 
end 
for i=1:max_row*max_col 
imwrite(seg{
     i},strcat('m',int2str(i),'.bmp')); %把第i帧的图片写为'mi.bmp'
保存
end 
%画出分块的边界
for row = 1:max_row 
 for col = 1:max_col 
 rectangle('Position',[32*(col-1),32*(row-1),32,32],... 
 'LineWidth',2,'LineStyle','-','EdgeColor','r'); 
 end 
end 
hold off 
%%===================================================================%%