动态规划-树形DP-习题
文章目录
- AcWing 1072. 树的最长路径
-
- 题目
- 题解
- 代码
- AcWing 1073. 树的中心
-
- 题目
- 题解
- 代码
- AcWing 1075. 数字转换
-
- 题目
- 题解
- 代码
- AcWing 1074. 二叉苹果树
-
- 题目
- 题解
- 代码
- AcWing 323. 战略游戏
-
- 题目
- 题解
- 代码
- AcWing 1077. 皇宫看守
-
- 题目
- 题解
- 代码
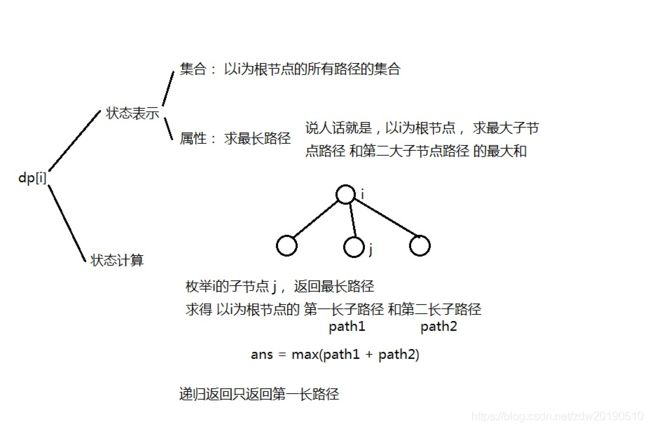
AcWing 1072. 树的最长路径
题目
6
5 1 6
1 4 5
6 3 9
2 6 8
6 1 7
输出样例:
22
题解
代码
// https://www.acwing.com/activity/content/code/content/1215928/
#include AcWing 1073. 树的中心
题目
5
2 1 1
3 2 1
4 3 1
5 1 1
输出样例:
2
题解
代码
// https://www.acwing.com/activity/content/code/content/1219105/
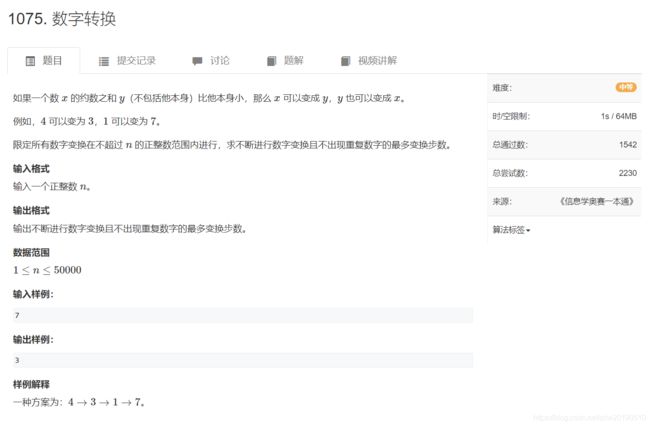
#include AcWing 1075. 数字转换
题目
题解
代码
// https://www.acwing.com/activity/content/code/content/1219611/
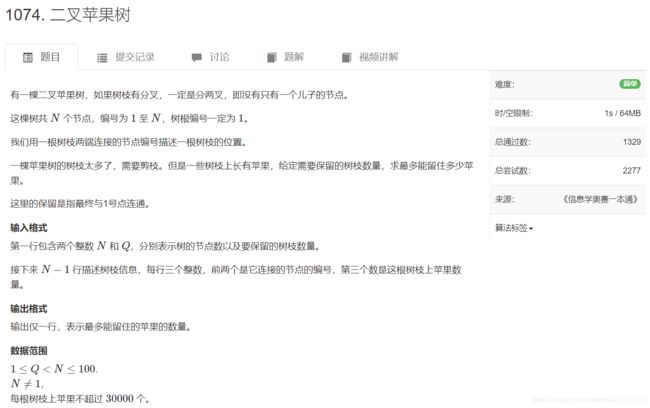
#include AcWing 1074. 二叉苹果树
题目
5 2
1 3 1
1 4 10
2 3 20
3 5 20
输出样例:
21
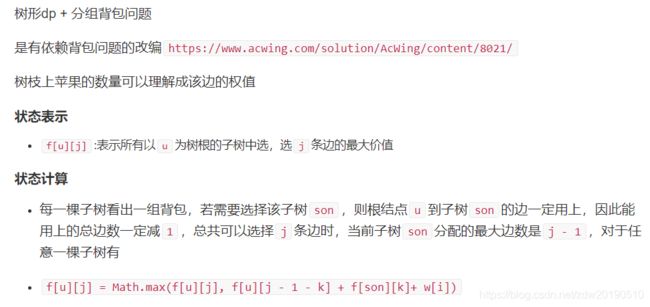
题解
代码
// https://www.acwing.com/activity/content/problem/content/1305/1/
#include AcWing 323. 战略游戏
题目
4
0:(1) 1
1:(2) 2 3
2:(0)
3:(0)
5
3:(3) 1 4 2
1:(1) 0
2:(0)
0:(0)
4:(0)
输出样例:
1
2
题解
代码
#include AcWing 1077. 皇宫看守
题目
6
1 30 3 2 3 4
2 16 2 5 6
3 5 0
4 4 0
5 11 0
6 5 0
输出样例:
25
样例解释:
在2、3、4结点安排护卫,可以观察到全部宫殿,所需经费最少,为 16 + 5 + 4 = 25。
题解
这个题初看与AcWing 323. 战略游戏 ,但是仔细分析,发现战略游戏的不选的点中间最多只能空一个,所以只需要记录两个状态,但是这个题可以出现不选的点中间只能空;两个,例如A->B->C->D,可以选择A和D,所以这里需要记录三个状态
* 分为3种状态
* f[i][0] 表示节点i被父结点看到的所有情况中的最小花费
* f[i][1] 表示节点i被子节点看到的所有情况中的最小花费
* f[i][2] 表示节点i上摆放侍卫的所用情况中的最小花费
*
* 状态计算:
* f[i][0] = min (f[j][2], f[j][1]) 点i是没有侍卫的,因此子节点只能有这两种情况
* f[i][2] = min (f[j][2], f[j][0], f[j][1]) 点i有侍卫,子节点可以被i影响到,因此有3种情况
*
* f[i][1] = min(f[j][1], f[j][2]) + f[k][2]
* 第3种情况较为复杂:如果结点i被子节点看到,那么说明,子节点有侍卫,i没有侍卫
* 那么在所有的集合情况中,应该找到子节点有侍卫的最小花费假定为f[k][2], 再加上其他子节点的花费情况,
* 而其他子节点的情况为min(f[j][1], f[j][2])(由于i没有侍卫,子节点可以表示为放侍卫或者被子节点影响)
*
* 观察第一种状态的计算,f[i][0] = min (f[j][2], f[j][1]),
* 其实可以得出第3种状态中的min(f[j][1], f[j][2])就相当于f[i][0] 减去 找到的某一个子节点的最小花费
* (因为第一种状态是包含了所有子节点的情况, 而当前找出除开某个子节点的其他情况)
* (在这种情况下,要除去的子节点的最小花费下相当于min(f[j][1], f[j][2]), 因为父亲节点是没有侍卫的)
* 因此 f[i][1] = min (f[i][1], f[i][0] - min(f[j][1], f[j][2]) + f[j][2])
代码
// https://www.acwing.com/activity/content/code/content/1222553/
#include