一、作用
在图中寻找从起点到终点的最优路径
二、使用
1.思路
A* 算法是启发式搜索,是一种尽可能基于现有信息的搜索策略。在搜索最短路径上下一个节点时利用估价函数对节点进行评估,选择可能性大的节点,从而提高了搜索过程的效率。
1)估价函数
g(j):从起点到节点 j 的实际路径代价
h*(j):节点 j 到目的节点的估计代价
2)h*(j) 的设计
欧几里得距离
计算量大,不适用于海量数据的路径规划。-
曼哈顿距离
此估价函数计算量小,虽然不是严格的方向优先,但基本能保证最短路径的搜索方向向目标点的方向进行。
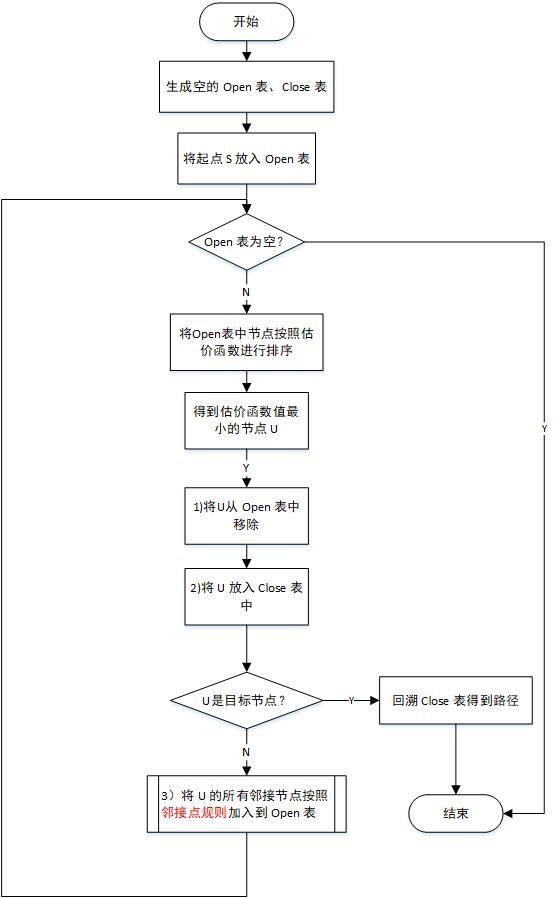
2.算法流程
A* 算法在搜索中设置两个表:
- Open 表
存储可被访问的节点 - Close 表
存储已被访问过的节点(最优路径上的节点)
Q:算法结束条件?
Open 表为空(想找最优路径但是已经无路可找了)或终点已经加入到了 Close 表中(说明最优路径已经找到)
Q:每次从 Open 表中取出 f 值最小的点出来所需做的操作?
Step1. 将该节点从 Open 表中移除;
Step2. 将该节点加入到 Close 表中;
Step3. 将该节点的所有邻接节点按照邻接点规则加入到 Open 表中
Q:什么是邻接点规则?
当前节点n
for (当前节点n的每个邻接子节点X) {
if (X 在 Close 表中) {
continue;
} else {
if (X 在 Open 表中) {
if (X的G值 > n的G值 + edges[n][X]) {
更新X的G值;
将X的父节点设置为n;
}
} else {
// 不在 Close && 不在Open
将X的父节点设置为n;
求出相应的 G、 H、 F;
将节点加入到Open表;
}
}
}
Q:如何得到从起点到终点的路径?
路径的存储结构类似于树的双亲存储结构。在Close 表中从终点回溯到起点得到最终路径。
3.题目
用 A* 算法求下图中 0 节点到 5 节点的最优路径。
各个节点坐标及边权值图示
用下面代码构造图
1)数学建模
a)Open 表中的节点信息存储结构
- 保存父节点
- G、H、F值
- 节点编号
/**
* 存储 Open 表中节点
*/
public static class AStarNode implements Comparable < AStarNode > {
// 节点在数组中编号
int nodeIndex;
// 实际距离
double gDis;
// 估计距离
double hDis;
// f(j)估价函数
double fj;
// 父节点
AStarNode parentNode;
public AStarNode() {}
public AStarNode(int nodeIndex, double gDis, double hDis, AStarNode parentNode) {
this.nodeIndex = nodeIndex;
this.gDis = gDis;
this.hDis = hDis;
this.fj = gDis + hDis;
this.parentNode = parentNode;
}
public AStarNode(int nodeIndex, double g, double h) {
this.nodeIndex = nodeIndex;
this.gDis = g;
this.hDis = h;
this.fj = g + h;
parentNode = null;
}
@Override
public int compareTo(AStarNode o) {
if (o == null) return -1;
if (fj > o.fj)
return 1;
else if (fj < o.fj) {
return -1;
} else {
return 0;
}
}
}
2)A* 算法代码
代码中图的存储结构是“前向关联边存储结构”
package com.whw.service.impl;
import com.whw.dao.EdgeDao;
import com.whw.dao.NodeDao;
import com.whw.model.Edge;
import com.whw.model.MyGraph;
import com.whw.model.NavPath;
import com.whw.model.Node;
import com.whw.service.NavigateService;
import com.whw.util.NavigationUtil;
import org.springframework.stereotype.Service;
import org.springframework.transaction.annotation.Transactional;
import javax.annotation.Resource;
import java.util.*;
/**
* 最短路径相关算法
*/
@Service
@Transactional
public class NavigateServiceImpl implements NavigateService {
/**
* 得到 startNodeNum 到 endNodeNum 之间的最短路径(A*算法)
*
* @param startNodeIndex:起点在数组中编号
* @param endNodeIndex:终点在数组中编号
* @return
*/
public NavPath getShortestRoad_AStar(MyGraph g, int startNodeIndex, int endNodeIndex) {
PriorityQueue < AStarNode > open = new PriorityQueue < > ();
List < AStarNode > close = new ArrayList < > ();
List < Double > gj = new ArrayList < > ();
// 将起始节点加入到 open 表中
double man = calManhattan(g, startNodeIndex, endNodeIndex);
open.add(new AStarNode(startNodeIndex, 0, man));
while (!open.isEmpty()) {
// 1.将 open 表中 fj 最小的节点从open中移除
AStarNode temp = open.remove();
// 2.加入到 Close 中
close.add(temp);
// 加入到 Close 的同时,更新 gj 中相应节点对应的值
if (gj.isEmpty()) {
gj.add(0.0);
} else {
gj.add(gj.get(gj.size() - 1) + NavigationUtil.getEdgeWight(g, close.get(close.size() - 1).nodeIndex, close.get(close.size() - 2).nodeIndex));
}
// 判断是否找到终点
if (temp.nodeIndex == endNodeIndex) {
// 找到终点
NavPath res = getNavPath(g, close, gj);
return res;
}
// 3.将该节点 temp 的所有邻接节点按照邻接点规则加入到 Open 表中
int beginIndex = g.nodes[temp.nodeIndex].getLinkEdgesBeginIndex();
int count = g.nodes[temp.nodeIndex].getCount();
if (beginIndex == -1) {
continue;
}
for (int i = beginIndex; i < beginIndex + count; i++) {
// 邻接节点
Node adjNode = g.edges[i].getExitNode();
int adjIndex = NavigationUtil.getIndex(g, adjNode.getNodeId());
// 邻接点规则
if (nodeIsInClose(adjIndex, close)) {
continue;
} else {
// adjNode 不在 close 表中
AStarNode p = getNodeInOpen(adjIndex, open);
if (p != null) {
// adjNode 在 Open 表
// 更新估价函数
double tempGDis = temp.gDis + NavigationUtil.getEdgeWight(g, temp.nodeIndex, adjIndex);
p.fj = tempGDis < p.gDis ? tempGDis + p.hDis : p.fj;
// 更新父节点
p.parentNode = temp;
} else {
// adjNode 不在 Open 表:将 adjNode 加入到 Open 表
double gDis = temp.gDis + NavigationUtil.getEdgeWight(g, temp.nodeIndex, adjIndex);
double mDis = calManhattan(g, adjIndex, endNodeIndex);
open.add(new AStarNode(adjIndex, gDis, mDis, temp));
}
}
}
}
return null;
}
/**
* 判断节点 adjIndex(节点在数组中编号) 是否在 Close 表中
* @param adjIndex
* @param close
* @return
*/
private boolean nodeIsInClose(int adjIndex, List < AStarNode > close) {
for (int i = 0; i < close.size(); i++) {
if (close.get(i).nodeIndex == adjIndex) {
return true;
}
}
return false;
}
/**
* 从 Open 表中得到 数组编号为 adjIndex 的节点,若 Open表中没有该节点则返回 null
* @param adjIndex
* @param open
* @return
*/
private AStarNode getNodeInOpen(int adjIndex, PriorityQueue < AStarNode > open) {
if (open != null && open.size() != 0) {
Iterator < AStarNode > iterator = open.iterator();
while (iterator.hasNext()) {
AStarNode node = iterator.next();
if (adjIndex == node.nodeIndex) {
return node;
}
}
}
return null;
}
/**
* 得到导航路径:从起始点到目标节点
*
* @param close
* @param gj
* @return
*/
private NavPath getNavPath(MyGraph g, List < AStarNode > close, List < Double > gj) {
NavPath path = new NavPath();
Stack < Node > stack = new Stack < > ();
if (close != null && close.size() != 0) {
// 输出路径
// Node parent = gDis.nodes[.nodeIndex];
AStarNode parent = close.get(close.size() - 1);
while (parent != null) {
stack.add(g.nodes[parent.nodeIndex]);
parent = parent.parentNode;
}
List < Node > nodes = new ArrayList < > ();
while (!stack.isEmpty()) {
nodes.add(stack.pop());
}
path.nodeList = nodes;
path.weight = gj.get(gj.size() - 1);
return path;
}
return null;
}
/**
* 计算两点间的曼哈顿距离
*
* @param g
* @param startNodeIndex
* @param endNodeIndex
* @return
*/
private double calManhattan(MyGraph g, int startNodeIndex, int endNodeIndex) {
Node p1 = g.nodes[startNodeIndex];
Node p2 = g.nodes[endNodeIndex];
return Math.abs(p1.getLatitude() - p2.getLatitude()) + Math.abs(p1.getLongtitude() - p2.getLongtitude());
}
}
3)构造图
public static MyGraph createMyGraph() {
// 节点数
int N = 8;
// 边数
int M = 16;
MyGraph g = new MyGraph(N, M);
// 节点信息
String[] nodeInfo = {
"10 C 0 0",
"11 D 1 2",
"12 E 2 3",
"13 F 3 4",
"14 G 4 4",
"15 H 5 5",
"16 I 2 1",
"17 J 3 2"
};
for (int i = 0; i < N; i++) {
Node node = new Node();
String[] info = nodeInfo[i].split(" ");
node.setNodeId(info[0]);
node.setNodeName(info[1]);
node.setLatitude(Double.parseDouble(info[2]));
node.setLongtitude(Double.parseDouble(info[3]));
g.nodes[i] = node;
}
// 边信息
String[] edgeInfo = {
"10 11 2",
"11 10 2",
"11 12 1",
"11 16 1",
"12 11 1",
"12 13 1",
"13 12 1",
"13 14 0.5",
"14 13 0.5",
"14 17 2",
"14 15 1",
"15 14 1",
"16 11 1",
"16 17 1",
"17 16 1",
"17 14 2"
};
for (int i = 0; i < M; i++) {
String[] info = edgeInfo[i].split(" ");
String id1 = info[0];
String id2 = info[1];
double weight = Double.parseDouble(info[2]);
Edge edge = new Edge();
edge.setEnterNode(new Node(id1));
edge.setExitNode(new Node(id2));
edge.setWeight(weight);
g.edges[i] = edge;
}
// 边关联信息
// 将节点按照节点编号升序排列,边集按照起始节点的编号升序排列
Arrays.sort(g.edges);
int k = 0; // linkedEdges[]中可用的最新位置
int index = 0; // 上一节点搜索结束后在弧集中的索引
for (int i = 0; i < N; i++) {
// 对于每一个节点:从弧集中找出从该节点发出的弧
Node node = g.nodes[i];
int count = 0;
int beginIndex = k;
while (index < g.edges.length && g.edges[index].getEnterNode().getNodeId().equals(node.getNodeId())) {
// 如果是该节点发出的弧
count++; // 个数加1
// g.linkedEdges[k++]=g.edges[index].edgeId;// 将该弧存起来
g.linkedEdges[k++] = index; // 将该弧在数组中的下标存起来
index++; // 判断下一个弧如何
}
// 所有的弧都判断完后
if (count == 0) {
// 该节点没有任何弧发出
node.setCount(0);
node.setLinkEdgesBeginIndex(-1);
} else {
node.setCount(count);
node.setLinkEdgesBeginIndex(beginIndex);
}
}
return g;
}
导航路径规划之五 A*算法
A星算法(Java实现)