重排九宫——C++实现BFS DFS搜索

重排九宫——C++实现BFS DFS搜索

参考链接:暴力美学之广度搜索求解重排九宫格问题.

你好！ 这是我第一次使用 Markdown编辑器 所展示的欢迎页。重排九宫问题，是人工智能领域涉及搜索策略的经典问题，即在3X3的正方形方格中排列八个元素，利用空位将其一步步移动从而寻找最优解路径的过程，其中最为常见解决这个问题的算法是广度优先算法，其优点是具有完备性。而且总是能找到最优解，缺点是面对过于复杂的情况，计算量较大，受制于计算资源。我的工作主要是在godgreen暴力美学的基础上进一步优化架构，并实现深度优先算法对九宫格实现重排。DFS的思想是从一个顶点V0开始，沿着一条路一直走到底，如果发现不能到达目标解，那就返回到上一个节点，然后从另一条路开始走到底。

关键代码段

1、OPEN表

（1）OPEN表节点放入CLOSE表

				//与广度优先不同的关键点1
				for (int i = 0; i <= 2; i++) {
     
					for (int j = 0; j <= 2; j++)
						close[closenumber].jiugongge[i][j] = open[opennumber].jiugongge[i][j];
				}
				close[closenumber].deepnumber = open[opennumber].deepnumber;
				close[closenumber].father = open[opennumber].father;

BFS从OPEN表头开始，DFS从OPEN表尾（刚刚放入的节点开始）

（2）OPEN表节点的删除

				//与广度优先不同的关键点2
				open[opennumber] = open[opennumber + 1];
				opennumber--;

2、CLOSE表

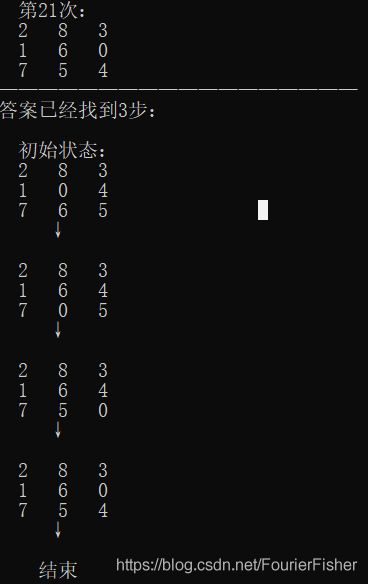
路径展示

				printf_s("  第%d次：\r\n",closenumber+1);
				show(close[closenumber].jiugongge);

CLOSE表的队列顺序实际就是搜索顺序

3、成果展示

样例一

P145例题——机械工程出版社的《人工智能导论》
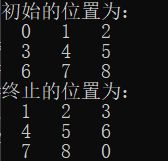
输入：
初始的位置为：
2 8 3
1 0 4
7 6 5
终止的位置为：
2 8 3
1 6 0
7 5 4

BFS输出：

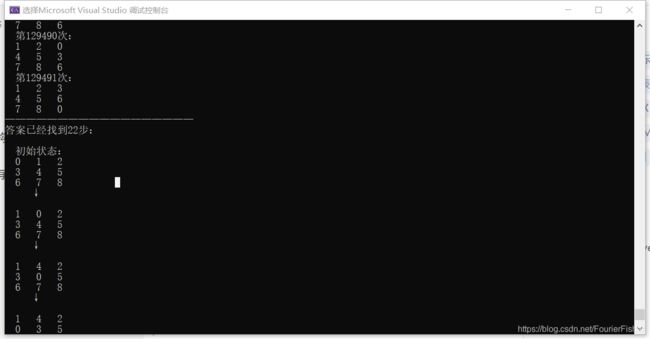
样例二

输入：

输出：

完整代码

// 重排九宫问题.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
#include 
#include 
#include
using namespace std;
//定义广度搜索深度为8
int deepnum = 50;
//close表中的标记
int closenumber = 0;
//定义九宫格结构体
struct Jiugong {
     
	//搜索深度
	int deepnumber;
	//九宫格字符组
	char jiugongge[3][3] ;
	struct Jiugong* father;
};
struct Jiugong open[1000000];
struct Jiugong close[1000000];
//定义两个数组储存初始和终止九宫格状态
char start[3][3];
char final[3][3];
//定义九宫格初始状态函数
int opennumber;
//显示是否可以拓展
bool flag;
//检查是否到达结束状态
bool checked(char str[3][3], char str2[3][3]) {
     
	for (int i = 0; i < 3; i++) {
     
		for (int j = 0; j < 3; j++) {
     
			if (str[i][j] != str2[i][j]) {
     
				return false;
			}
		}
	}
	return true;
}
//判断九宫格是否已经存在
bool alreadyexit(struct Jiugong a, struct Jiugong b) {
     
	if (checked(a.jiugongge, b.jiugongge)) {
     
		return true;
	}
	else return false;
}
//寻找0所在位置
int findzero(char s[3][3]) {
     
	for (int i = 0; i <= 2; i++) {
     
		for (int j = 0; j <= 2; j++) {
     
			if (s[i][j] == '0')
				return i * 3 + j;
		}
	}
}

//打印九宫格
void show(char square[3][3]) {
     
	int i, j;
	for (i = 0; i <= 2; i++) {
     
		for (j = 0; j <= 2; j++) {
     
			printf_s("  %c ", square[i][j]);
		}
		printf_s("\r\n");
	}
}//展示需要完成移动的路径
void ShowRequire() {
     
	printf_s("初始的位置为：\r\n");
	show(start);
	printf_s("终止的位置为：\r\n");
	show(final);
}
//判断是否在close表中
bool inclose(char s[3][3]) {
     
	for (int m = 0; m <= closenumber; m++) {
     
		if (checked(s, close[m].jiugongge))
			return true;
	}
	return false;
}
//顺序输出
void inorder(struct Jiugong* root) {
     
	if (root == nullptr) {
     
		return;
	}
	else
		inorder(root->father);
	show(root->jiugongge);
	printf_s("     ↓  \r\n\r\n");

}
//判断是否可扩展 
bool able(char o[3][3]) {
     
	if (inclose(o)) {
     
		return false;
	}
	//当不在close表中时，放入open表中 
	else{
     
		opennumber++;
		for (int k = 0; k <= 2; k++) {
     
			for (int h = 0; h <= 2; h++) {
     
				open[opennumber].jiugongge[k][h] = o[k][h];
			}
		}
		open[opennumber].deepnumber = close[closenumber].deepnumber + 1;
		open[opennumber].father = &close[closenumber];
		return true;
	}
}
//初始化
void init() {
     
	//定义两个字符串存储用户输入
	string str1, str2;
	cout << "————当前局势————" << endl;
	cin >> str1;
	cout << "————目标局势————" << endl;
	cin >> str2;

	//初始化九宫格条件
	int index = 0;
	for (int i = 0; i < 3; i++)
	{
     
		for (int j = 0; j < 3; j++)
		{
     
			start[i][j] = str1[index];
			final[i][j] = str2[index];
			index++;
		}
	}
	//展示问题
	ShowRequire();
}
void BFS()
{
     
	//广度优先搜索
	//把初始节点放入open表中
	open[0].deepnumber = 0;
	for (int i = 0; i <= 2; i++) {
     
		for (int j = 0; j <= 2; j++)
			open[0].jiugongge[i][j] = start[i][j];
	}
	opennumber = 0;
	while (true)
	{
     
		//判断open表是否为空 
		if (!open[0].jiugongge) {
     
			printf_s("问题 无解在第0步停止");
			exit(100);
		}        //不为空
		else {
     
			while ((open[0].jiugongge[0][0] + open[0].jiugongge[2][2]) >= 1)
			{
     
				//将节点n放入close表中
				closenumber++;
				//close[closenumber].deepnumber = open[0].deepnumber;
				for (int i = 0; i <= 2; i++) {
     
					for (int j = 0; j <= 2; j++)
						close[closenumber].jiugongge[i][j] = open[0].jiugongge[i][j];
				}
				close[closenumber].deepnumber = open[0].deepnumber;
				close[closenumber].father = open[0].father;
				//显示搜索路径
				printf_s("  第%d次：\r\n", closenumber);
				show(close[closenumber].jiugongge);
				//删除open表中元素
				for (int l = 0; l < opennumber; l++) {
     
					open[l] = open[l + 1];
				}
				opennumber--;
				//判断节点n是否为目标节点
				if (checked(close[closenumber].jiugongge, final) == true) {
     
					printf_s("——————————————————\r\n");
					printf_s("答案已经找到%d步：\r\n\r\n", close[closenumber].deepnumber);
					printf_s("  初始状态：\r\n");
					inorder(&close[closenumber]);
					printf_s("    结束  \r\n\r\n");
					exit(100);
				}
				else {
     
					//拓展节点n
					int zero = findzero(close[closenumber].jiugongge);
					char check[3][3];
					//向左拓展
					if ((zero) % 3 != 0) {
     
						for (int k = 0; k <= 2; k++) {
     
							for (int h = 0; h <= 2; h++) {
     
								check[k][h] = close[closenumber].jiugongge[k][h];
							}
						}
						check[(zero / 3)][(zero % 3)] = check[zero / 3][zero % 3 - 1];
						check[(zero / 3)][(zero % 3 - 1)] = '0';
						flag = able(check);
					}
					//向上拓展
					if ((zero) / 3 != 0) {
     
						for (int k = 0; k <= 2; k++) {
     
							for (int h = 0; h <= 2; h++) {
     
								check[k][h] = close[closenumber].jiugongge[k][h];
							}
						}
						check[(zero / 3)][(zero % 3)] = check[zero / 3 - 1][zero % 3];
						check[(zero / 3) - 1][(zero % 3)] = '0';
						flag = able(check);
					}
					//向右拓展
					if ((zero) % 3 != 2) {
     

						for (int k = 0; k <= 2; k++) {
     
							for (int h = 0; h <= 2; h++) {
     
								check[k][h] = close[closenumber].jiugongge[k][h];
							}
						}
						check[(zero / 3)][(zero % 3)] = check[zero / 3][zero % 3 + 1];
						check[(zero / 3)][(zero % 3 + 1)] = '0';
						flag = able(check);
					}
					//向下拓展
					if ((zero) / 3 != 2) {
     
						for (int k = 0; k <= 2; k++) {
     
							for (int h = 0; h <= 2; h++) {
     
								check[k][h] = close[closenumber].jiugongge[k][h];
							}
						}
						check[(zero / 3)][(zero % 3)] = check[zero / 3 + 1][zero % 3];
						check[(zero / 3) + 1][(zero % 3)] = '0';
						flag = able(check);
					}
				}
				if (open[0].deepnumber > deepnum) {
     
					printf_s("\r\n很遗憾当前的搜索深度为%d，没有解！\r\n", deepnum);
					exit(100);
				}
			}

		}
	}
}
void DFS()
{
     
	//广度优先搜索
	//把初始节点放入open表中
	open[0].deepnumber = 0;
	for (int i = 0; i <= 2; i++) {
     
		for (int j = 0; j <= 2; j++)
			open[0].jiugongge[i][j] = start[i][j];
	}
	opennumber = 0;
	while (true)
	{
     
		//判断open表是否为空 
		if (!open[0].jiugongge) {
     
			printf_s("问题 无解在第0步停止");
			exit(100);
		}        //不为空
		else {
     
			while (true)
			{
     
				//将节点n放入close表中
				//与广度优先不同的关键点1
				for (int i = 0; i <= 2; i++) {
     
					for (int j = 0; j <= 2; j++)
						close[closenumber].jiugongge[i][j] = open[opennumber].jiugongge[i][j];
				}
				close[closenumber].deepnumber = open[opennumber].deepnumber;
				close[closenumber].father = open[opennumber].father;
				//显示搜索路径
				printf_s("  第%d次：\r\n",closenumber+1);
				show(close[closenumber].jiugongge);

				//删除open表中元素
				//与广度优先不同的关键点2
				open[opennumber] = open[opennumber + 1];
				opennumber--;
				//判断节点n是否为目标节点
				if (checked(close[closenumber].jiugongge, final) == true) {
     
					printf_s("——————————————————\r\n");
					printf_s("答案已经找到%d步：\r\n\r\n", close[closenumber].deepnumber );
					printf_s("  初始状态：\r\n");
					inorder(&close[closenumber]);
					printf_s("    结束  \r\n\r\n");
					exit(100);
				}
				else {
     
					//拓展节点n
					int zero = findzero(close[closenumber].jiugongge);
					char check[3][3];
					//向左拓展
					if ((zero) % 3 != 0) {
     
						for (int k = 0; k <= 2; k++) {
     
							for (int h = 0; h <= 2; h++) {
     
								check[k][h] = close[closenumber].jiugongge[k][h];
							}
						}
						check[(zero / 3)][(zero % 3)] = check[zero / 3][zero % 3 - 1];
						check[(zero / 3)][(zero % 3 - 1)] = '0';
						flag = able(check);
					}
					//向上拓展
					if ((zero) / 3 != 0) {
     
						for (int k = 0; k <= 2; k++) {
     
							for (int h = 0; h <= 2; h++) {
     
								check[k][h] = close[closenumber].jiugongge[k][h];
							}
						}
						check[(zero / 3)][(zero % 3)] = check[zero / 3 - 1][zero % 3];
						check[(zero / 3) - 1][(zero % 3)] = '0';
						flag = able(check);
					}
					//向右拓展
					if ((zero) % 3 != 2) {
     

						for (int k = 0; k <= 2; k++) {
     
							for (int h = 0; h <= 2; h++) {
     
								check[k][h] = close[closenumber].jiugongge[k][h];
							}
						}
						check[(zero / 3)][(zero % 3)] = check[zero / 3][zero % 3 + 1];
						check[(zero / 3)][(zero % 3 + 1)] = '0';
						flag = able(check);
					}
					//向下拓展
					if ((zero) / 3 != 2) {
     
						for (int k = 0; k <= 2; k++) {
     
							for (int h = 0; h <= 2; h++) {
     
								check[k][h] = close[closenumber].jiugongge[k][h];
							}
						}
						check[(zero / 3)][(zero % 3)] = check[zero / 3 + 1][zero % 3];
						check[(zero / 3) + 1][(zero % 3)] = '0';
						flag = able(check);
					}
				}
				if (open[0].deepnumber > deepnum) {
     
					printf_s("\r\n很遗憾当前的搜索深度为%d，没有解！\r\n", deepnum);
					exit(100);
				}
				closenumber++;
			}

		}
	}
}
int main() {
     
	init();
	printf_s("————广度优先————\r\n");
	BFS();
	printf_s("————深度优先————\r\n");
	DFS();
}

感悟

1、实现流程：节点表示（结构体）——构造树（指针）——查找策略（比对，对OPEN表节点的选择）
2、排序策略：OPEN表（待筛选队列，有顺序），CLOSE表（路径拓展，表内记录查询顺序）