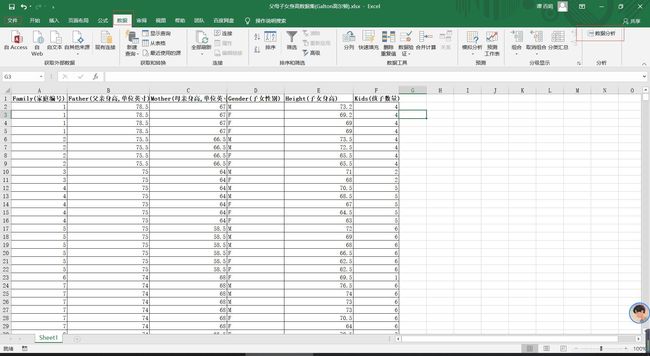
”父母子女身高“数据集(高尔顿数据集)进行线性回归分析实验
”父母子女身高“数据集(高尔顿数据集)进行线性回归分析实验
- 一、配置Excel
- 二、对数据做线性回归分析
- 三、父亲母亲分别与儿子做回归方程分析
-
- 1、父亲与儿女数据分析
- 2、母亲与儿女身高数据分析
一、配置Excel
实验将使用到Excel的数据分析工具,一般情况下是没有的,需要添加
选择‘文件’——>‘选项’——>‘加载项’——>‘分析工具库’——>‘确定’添加至数据版面中
二、对数据做线性回归分析
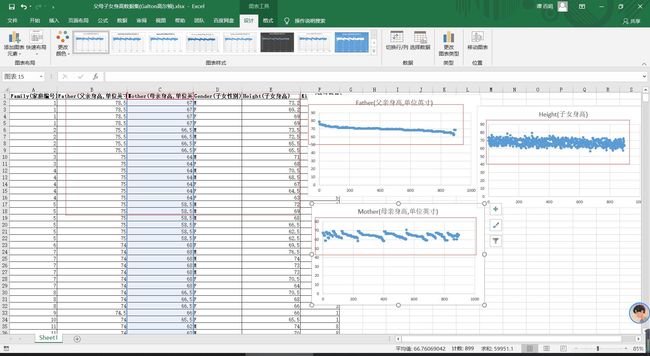
1、对数据散点图分析
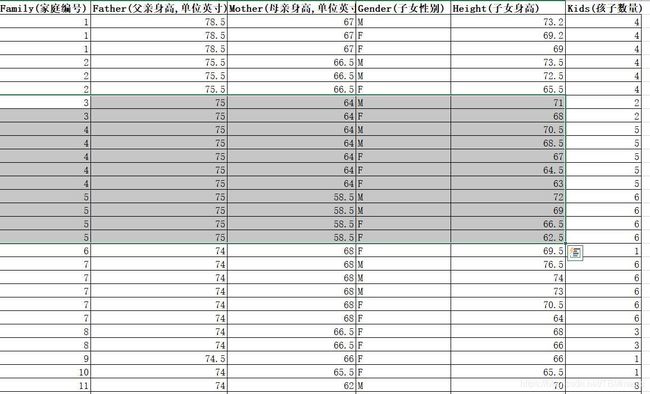
初步看出散点图中父母的身高数据还比较有迹可循,说明这组数据集是有规律的;同时,数据中有许多数据是重复的,我们先对数据进行去除重复的处理
在数据工具栏中找到删除重复值,同时选择所有的数据
2、做数据回归分析
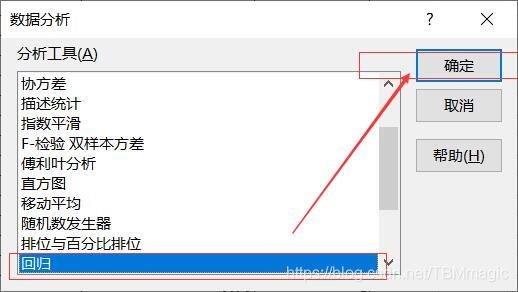
在数据分析工具中选择回归
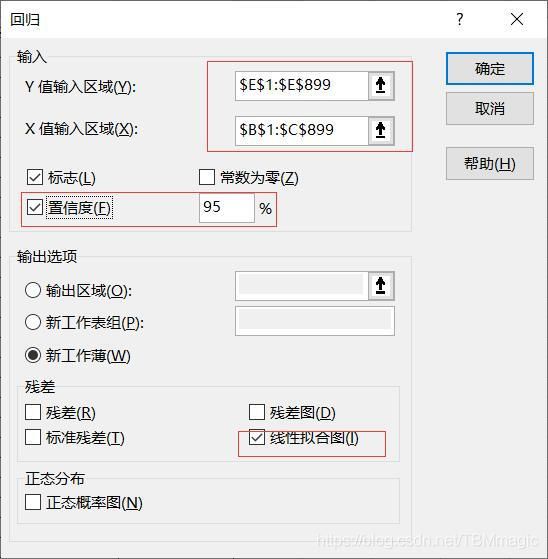
选择好X、Y数据的区域,如果要选择标题,则添加标志打勾,否则在所选数据中出现非数值会报错
分析完成后如图所示
我们先对几个表格的数据进行一些认识
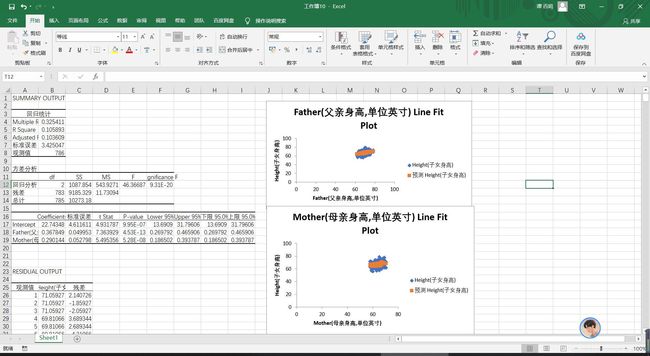
(1)第一部分:回归统计表
这一部分给出了相关系数、测定系数、校正测定系数、标准误差和样本数目如下
| 回归统计 | |
|---|---|
| Multiple R | 0.325411452 |
| R Square | 0.105892613 |
| Adjusted R Square | 0.103608814 |
| 标准误差 | 3.425046607 |
| 观测值 | 786 |
逐行说明如下:
Multiple对应的数据是相关系数(correlation+coefficient),即R=0.325411452。
R Square对应的数值为测定系数(determination+coefficient),或称拟合优度(goodness+of+fit),它是相关系数的平方,即有R2=0.3254114522=0.105892613。
Adjusted对应的是校正测定系数(adjusted+determination+coefficient)
标准误差(standard error)对应的即所谓标准误差
最后一行的观测值对应的是样本数目,即有n=786
(2)第二部分:方差分析表
方差分析部分包括自由度、误差平方和、均方差、F值、P值等
| 方差分析 | |||||
|---|---|---|---|---|---|
| df | SS | MS | F | Significance F | |
| 回归分析 | 2 | 1087.854 | 543.9271 | 46.36687 | 9.31238E-20 |
| 残差 | 783 | 9185.329 | 11.73094 | ||
| 总计 | 785 | 10273.18 |
逐列、分行说明如下:
第一列df对应的是自由度(degree of freedom),第一行是回归自由度dfr,等于变量数目,即dfr=m;第二行为残差自由度dfe,等于样本数目减去变量数目再减1,即有dfe=n-m-1;第三行为总自由度dft,等于样本数目减1,即有dft=n-1。对于本例,m=1,n=10,因此,dfr=1,dfe=n-m-1=8,dft=n-1=9。
第二列SS对应的是误差平方和,或称变差。第一行为回归平方和或称回归变差SSr;第二行为剩余平方和(也称残差平方和)或称剩余变差SSe,它表征的是因变量对其预测值的总偏差,这个数值越大,意味着拟合的效果越差。上述的y的标准误差即由SSe给出。第三行为总平方和或称总变差SSt;它表示的是因变量对其平均值的总偏差。容易验证1087.854+9185.329=10273.18
第三列MS对应的是均方差,它是误差平方和除以相应的自由度得到的商。第一行为回归均方差MSr;第二行为剩余均方差MSe
第四列对应的是F值,用于线性关系的判定。
第五列Significance F对应的是在显著性水平下的Fα临界值,其实等于P值,即弃真概率。所谓“弃真概率”即模型为假的概率,显然1-P便是模型为真的概率。可见P值是越小越好,其置信度随之越高
(3)第三部分,回归参数表
回归参数表包括回归模型的截距、斜率及其有关的检验参数
| Coefficients | 标准误差 | t Stat | P-value | Lower 95% | Upper 95% | 下限 95.0% | 上限 95.0% | |
|---|---|---|---|---|---|---|---|---|
| Intercept | 22.7434805 | 4.611611 | 4.931787 | 9.95E-07 | 13.69089635 | 31.79606 | 13.6909 | 31.79606 |
| Father(父亲身高,单位英寸) | 0.367848789 | 0.049953 | 7.363929 | 4.53E-13 | 0.269791545 | 0.465906 | 0.269792 | 0.465906 |
| Mother(母亲身高,单位英寸) | 0.290144236 | 0.052798 | 5.495356 | 5.28E-08 | 0.186501698 | 0.393787 | 0.186502 | 0.393787 |
第一列Coefficients对应的模型的回归系数,包括截距a=22.7434805和分别的斜率b=0.367848789/0.290144236,由此可以建立回归模型
第二列为回归系数的标准误差,误差值越小,表明参数的精确度越高
第三列t Stat对应的是统计量t值,用于对模型参数的检验,需要查表才能决定
第四列P value对应的是参数的P值。当P<0.05时,可以认为模型在α=0.05的水平上显著,或者置信度达到95%;当P<0.01时,同理可以认为置信度达到了99%;当P<0.001时,可以认为模型的置信度达到了99.9%。
(4)第四部分,残差输出结果
这一部分为选择输出内容,如果在“回归”分析选项框中没有选中有关内容,则输出结果不会给出这部分结果。
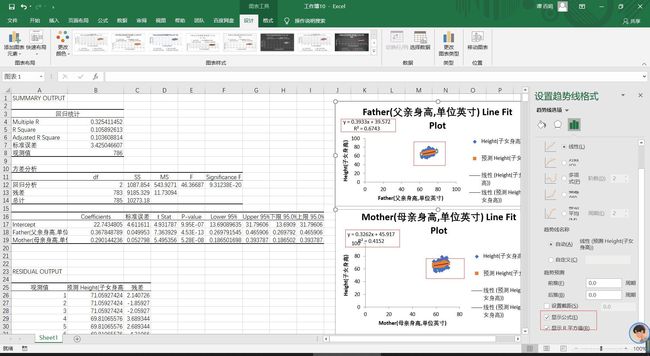
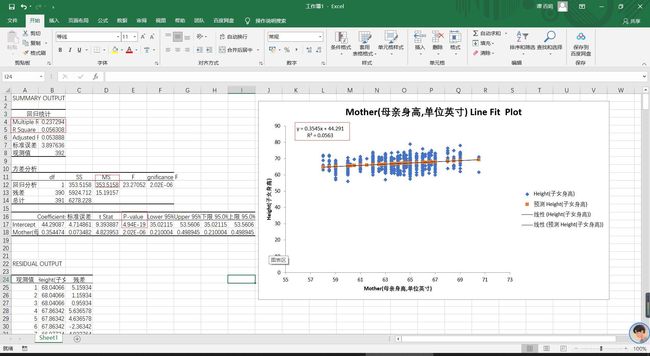
认识完了之后,我们点击生成的回归散点图进行绘制趋势线,并显示出来回归方程和R平方值
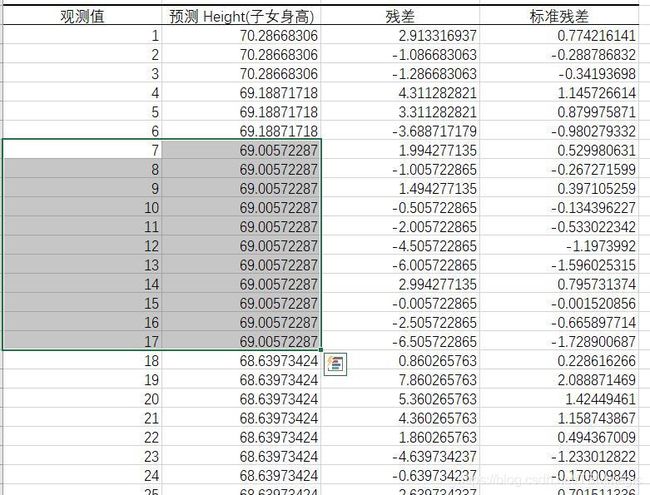
由表和图可读出
相关系数R=0.325411452、均方差为MS=543.9271、P值为9.95^-7。由上我们便可以得出父母与儿子的回归方程y=22.743+0.367x1+0.29x2
三、父亲母亲分别与儿子做回归方程分析
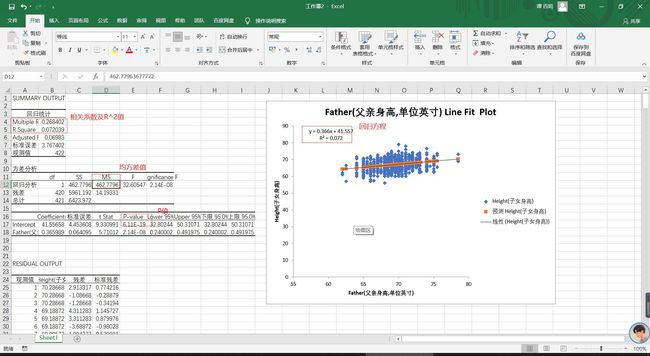
1、父亲与儿女数据分析
与上同样的做数据重复删除处理
同样做数据分析后得出回归方程及R2的值
由此图的R^2值可以看出,父亲身高与子女身高的线性相关性较弱。P值远小于0.01,其表明得到的回归方程是可靠的
由原数据表和得出的预测值表相对比,我们可以预测到如果父亲的身高为75英寸,则女儿身高为69.005
2、母亲与儿女身高数据分析
同上做删除重复数据处理
做同上操作,数据处理后如下图显示
其中P值远小于0.01,其方程是可靠的。其中R^2值0.05,表明其线性相关程度不高
综上我们可以知道,父母身高对儿女身高的影响度并没有太大的关系