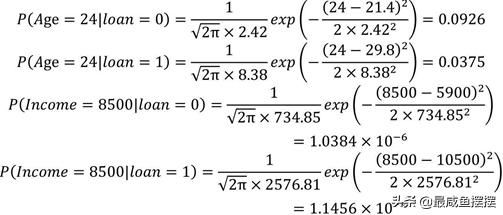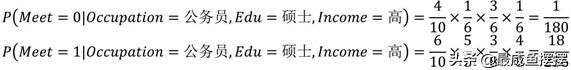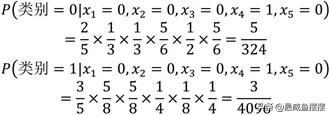基于朴素贝叶斯分类器的西瓜数据集 2.0 预测分类_第十章:利用Python实现朴素贝叶斯模型
免责声明:本文是通过网络收集并结合自身学习等途径合法获取,仅作为学习交流使用,其版权归出版社或者原创作者所有,并不对涉及的版权问题负责。若原创作者或者出版社认为侵权,请联系及时联系,我将立即删除文章,十分感谢!
注:来源刘顺祥《从零开始学Python数据分析与挖掘》,版权归原作者或出版社所有,仅供学习使用,不用于商业用途,如有侵权请留言联系删除,感谢合作。
10.1 朴素贝叶斯理论基础
在介绍如何使用贝叶斯概率公式计算后验概率之前,先回顾一下概率论与数理统计中的条件概率和全概率公式:
如上等式为条件概率的计算公式,表示在已知事件A的情况下事件B发生的概率,其中P(AB)表示事件A与事件B同时发生的概率。所以, 根据条件概率公式得到概率的乘法公式:P(AB)=P(A)P(B|A)=P(B)P(A|B)。
如上等式为全概率公式,其中事件B1,B2,…,Bn构成了一个完备的事件组,并且每一个P(Bi)均大于0。该公式表示,对于任意的一个事件A来说,都可以表示成n个完备事件组与其乘积的和。
在具备上述的基础知识之后,再来看看贝叶斯公式。如前文所说, 贝叶斯分类器的核心就是在已知X的情况下,计算样本属于某个类别的概率,故这个条件概率的计算可以表示为:
其中,Ci表示样本所属的某个类别。假设数据集的因变量y一共包含k个不同的类别,故根据全概率公式,可以将上式中的分母表示成
;再根据概率的乘法公式,可以将上式中的分子重新改写为P(Ci)P(X|Ci)。对于上面的条件概率公式而言,样本最终属于哪个类别Ci,应该将计算所得的最大概率值P(Ci|X)对应的类别作为样本的最终分类,所以上式可以表示为:
如上公式所示,对于已知的X,朴素贝叶斯分类器就是计算样本在各分类中的最大概率值。接下来详细拆解公式中的每一个部分,为获得条件概率的最大值,寻找最终的影响因素。分母是一个常量,它与样本属于哪个类别没有直接关系,所以计算P(Ci|X)的最大值就转换成了计算分子的最大值,即argmax P(Ci)P(X|Ci);如果分子中的P(Ci)项未知的话,一般会假设每个类别出现的概率相等,只需计算P(X|Ci)的最大值,然而在绝大多数情况下,P(Ci)是已知的,它以训练数据集中类别Ci的频率作为先验概率, 可以表示为NCi/N。所以,现在的主要任务就是计算P(X|Ci)的值,即已知某个类别的情况下自变量X为某种值的概率。假设数据集一共包含p个自变量,则X可以表示成(x1,x2,…,xp),进而条件概率P(X|Ci)可以表示为:P(X|Ci)=P(x1,x2,…,xp|Ci)很显然,条件联合概率值的计算还是比较复杂的,尤其是当数据集的自变量个数非常多的时候。为了使分类器在计算过程中提高速度,提出了一个假设前提,即自变量是条件独立的(自变量之间不存在相关 性),所以上面的计算公式可以重新改写为:
P(X|Ci)=P(x1,x2,…,xp|Ci)=P(x1|Ci)P(x2|Ci)…P(xp|Ci)
如上式所示,将条件联合概率转换成各条件概率的乘积,进而可以大大降低概率值P(X|Ci)的运算时长。但问题是,在很多实际项目的数据集中,很难保证自变量之间满足独立的假设条件。根据这条假设,可以得到一般性的结论,即自变量之间的独立性越强,贝叶斯分类器的效果就会越好;如果自变量之间存在相关性,就会在一定程度提高贝叶斯分类器的错误率,但通常情况下,贝叶斯分类器的效果不会低于决策树。
接下来的章节将介绍如何计算P(Ci)P(x1|Ci)P(x2|Ci)…P(xp|Ci)的最大概率值,从而实现一个未知类别样本的预测。
10.2 几种贝叶斯模型
自变量X的数据类型可以是连续的数值型,也可以是离散的字符 型,或者是仅含有0-1两种值的二元类型。通常会根据不同的数据类型选择不同的贝叶斯分类器,例如高斯贝叶斯分类器、多项式贝叶斯分类器和伯努利贝叶斯分类器,下面将结合案例详细介绍这几种分类器的使用方法。
10.2.1 高斯贝叶斯分类器
如果数据集中的自变量X均为连续的数值型,则在计算P(X|Ci)时会假设自变量X服从高斯正态分布,所以自变量X的条件概率可以表示成:
其中,xj表示第j个自变量的取值,μji为训练数据集中自变量xj属于类别Ci的均值,σji为训练数据集中自变量xj属于类别Ci的标准差。所以, 在已知均值μji和标准差σji时,就可以利用如上的公式计算自变量xj取某种值的概率。
为了使读者理解P(xj|Ci)的计算过程,这里虚拟一个数据集,并通过手工的方式计算某个新样本属于各类别的概率值。
如表10-1所示,假设某金融公司是否愿意给客户放贷会优先考虑两个因素,分别是年龄和收入。现在根据已知的数据信息考察一位新客 户,他的年龄为24岁,并且收入为8500元,请问该公司是否愿意给客户放贷?手工计算P(Ci|X)的步骤如下:
(1) 因变量各类别频率
P(loan=0)=5/10=0.5
P(loan=1)=5/10=0.5
(2) 均值
μAge0=21.40 μAge1=29.8
μIncome0=5900 μIncome1=10500
(3) 标准差
σAge0=2.42 σAge1=8.38
σIncome0=734.85 σIncome12576.81
(4) 单变量条件概率
(5) 贝叶斯后验概率
P(loan=0|Age=24,Income=8500)
=P(loan=0)×P(Age=24|loan=0)×P(Income=8500|loan=0)
=0.5×0.0926×1.0384×10-6=4.8079×10-8
P(loan=1|Age=24,Income=8500)
=P(loan=1)×P(Age=24|loan=1)×P(Income=8500|loan=1)
=0.5×0.0375×1.1456×10-4=2.1479×10-6
经过上面的计算可知,当客户的年龄为24岁,并且收入为8500时, 被预测为不放贷的概率是4.8079×10-8,放贷的概率为2.1479×10-6,所以根据argmax P(Ci)P(X|Ci)的原则,最终该金融公司决定给客户放贷。
高斯贝叶斯分类器的计算过程还是比较简单的,其关键的核心是假设数值型变量服从正态分布,如果实际数据近似服从正态分布,分类结果会更加准确。sklearn模块提供了实现该分类器的计算功能,它就是naive_bayes子模块中的GaussianNB类。首先介绍一下该“类”的语法和参数含义:
GaussianNB(priors=None)priors:用于指定因变量各类别的先验概率,默认以数据集中的类别频率作为先验概率。
由于该“类”仅包含一个参数,且参数的默认值是以各类别的频率作为先验概率,因此在调用GaussianNB类构造高斯贝叶斯分类器时,可以不传递任何参数值,接下来利用该分类器实现面部皮肤区分的判别。
10.2.2 高斯贝叶斯分类器的应用
面部皮肤区分数据集来自于UCI网站,该数据集含有两个部分,一部分为人类面部皮肤数据,该部分数据是由不同种族、年龄和性别人群的图片转换而成的;另一部分为非人类面部皮肤数据。两个部分的数据集一共包含245 057条样本和4个变量,其中用于识别样本是否为人类面部皮肤的因素是图片中的三原色R、G、B,它们的值均落在0~255;因变量为二分类变量,表示样本在对应的R、G、B值下是否为人类面部皮肤,其中1表示人类面部皮肤,2表示非人类面部皮肤。
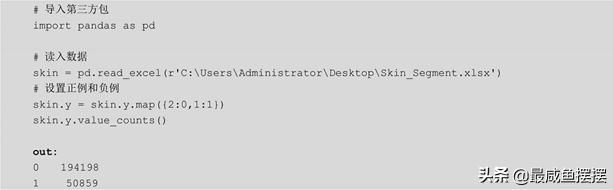
通常情况下,研究人员会对样本是否为人类面部皮肤更加感兴趣, 所以需要将原始数据集中因变量为1的值设置为正例、因变量为2的值设置为负例,代码如下:
如上结果所示,因变量0表示负例,说明样本为非人类面部皮肤, 一共包含194198个观测;因变量1表示正例,说明样本为人类面部皮肤,一共包含50 859个观测;因变量值为0和1之间的比例为5:1。接下来将该数据集拆分为训练集和测试集,分别用于模型的构建和模型的评 估,代码如下:
如上结果所示,通过构建高斯朴素贝叶斯分类器,实现测试数据集上的预测,经统计,预测为负例的一共有50 630条样本、预测为正例的一共有10 635条样本。为检验模型在测试数据集上的预测效果,需要构建混淆矩阵和绘制ROC曲线,其中混淆矩阵用于模型准确率、覆盖率、精准率指标的计算;ROC曲线用于计算AUC值,并将AUC值与0.8相比,判断模型的拟合效果,代码如下:
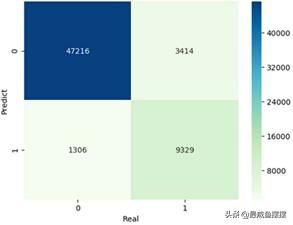
见图10-1。
如图10-1所示,将混淆矩阵做了可视化处理,其中主对角线的数值表示正确预测的样本量,剩余的4720条样本为错误预测的样本。经过对混淆矩阵的计算,可以得到模型的整体预测准确率为92.30%;进一步可以得到每个类别的预测精准率(precision=正确预测某类别的样本量/该类别的预测样本个数)和覆盖率(recall=正确预测某类别的样本量/该类别的实际样本个数),通过准确率、精准率和覆盖率的对比,模型的预测效果还是非常理想的。接下来绘制ROC曲线,用于进一步验证得到的结论,代码如下:
见图10-2。
如图10-2所示的ROC曲线,计算得到的AUC值为0.94,超过用于评判模型好坏的阈值0.8,故可以认为构建的贝叶斯分类器是非常理想的,进而验证了前文所得的结论。最后需要强调的是,利用高斯贝叶斯分类器对数据集进行分类时要求输入的数据集X为连续的数值型变量。
10.2.3 多项式贝叶斯分类器
如果数据集中的自变量X均为离散型变量,就无法使用高斯贝叶斯分类器,而应该选择多项式贝叶斯分类器。在计算概率值P(X|Ci)时,会假设自变量X的条件概率满足多项式分布,故概率值P(X|Ci)的计算公式可以表示为:
其中,xjk表示自变量xj的取值;Nik表示因变量为类别Ci时自变量xj取xjk的样本个数;Ni表示数据集中类别Ci的样本个数;α为平滑系数,用于防止概率值取0可能,通常将该值取为1,表示对概率值做拉普拉斯平 滑;n表示因变量的类别个数。
同样,为了使读者理解P(xj=xjk|Ci)的计算过程,这里虚拟一个离散型自变量的数据集,并通过手工方式计算某个新样本属于各类别的概率值。
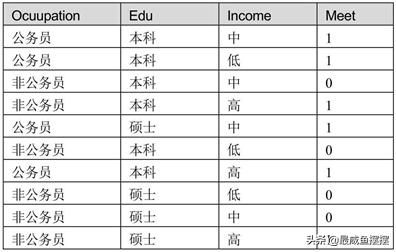
如表10-2所示,假设影响女孩是否参加相亲活动的重要因素有三 个,分别是男孩的职业、受教育水平和收入状况;如果女孩参加相亲活动,则对应的Meet变量为1,否则为0。请问在给定的信息下,对于高收入的公务员,并且其学历为硕士的男生来说,女孩是否愿意参与他的相亲?接下来通过手动的方式,计算女生是否与该男生见面的概率,步骤如下:
(1) 因变量各类别频率
P(Meet=0)=4/10=0.4 P(Meet=1)=6/10=0.6
(2) 单变量条件概率
(3) 贝叶斯后验概率
经计算发现,当男生为高收入的公务员,并且受教育水平也很高 时,女生愿意见面的概率约为0.0703、不愿意见面的概率约为0.0056。所以根据argmaxP(Ci)P(X|Ci)的原则,最终女生会选择参加这位男生的相亲。
需要注意的是,如果在某个类别样本中没有出现自变量xj取某种值的观测时,条件概率P(xj=xjk|Ci)就会为0。例如,当因变量Meet为0时, 自变量Occupation中没有取值为公务员的样本,所以就会导致单变量条件概率为0,进而使得P(Ci)P(X|Ci)的概率为0。为了避免贝叶斯后验概率为0的情况,会选择使用平滑系数α,这就是为什么自变量X的条件概率写成P(xj=xjk|Ci)= 的原因。
多项式贝叶斯分类器的计算过程也同样比较简单,读者如需使用Python实现该分类器的构造,可以直接导入sklearn的子模块naive_bayes 模块,然后调用MultinomialNB类。有关该“类”的语法和参数含义如 下:
MultinomialNB(alpha = 1.0, fit_prior = True, class_prior = Nalpha:用于指定平滑系数α的值,默认为1.0。fit_prior:bool类型参数,是否以数据集中各类别的比例作为P(Ci)的先验概率,默认为True。
class_prior:用于人工指定各类别的先验概率P(Ci),如果指定该参数,则参数fit_prior不再有效。
为了使读者理解多项式贝叶斯分类器的功效,接下来将使用MultinomialNB类进行项目实战,实战的内容就是根据蘑菇的各项特征判断其是否有毒。
10.2.4 多项式贝叶斯分类器的应用
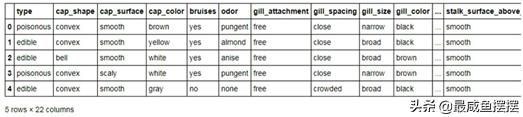
蘑菇数据集来自于UCI网站,一共包含8 124条观测和22个变量,其中因变量为type,表示蘑菇是否有毒,剩余的自变量是关于蘑菇的形 状、表面光滑度、颜色、生长环境等。首先将该数据集读入Python,并预览前5行数据,代码如下:
# 读取数据mushrooms = pd.read_csv(r'C:甥敳獲AdministratorDesktopmus # 数据的前5行,见表10-3mushrooms.head()如表10-3所示,表中的所有变量均为字符型的离散值,由于Python 建模过程中必须要求自变量为数值类型,因此需要对这些变量做因子化处理,即把字符值转换为对应的数值。接下来利用pandas模块中的factorize函数对离散的自变量进行数值转换,代码如下:
# 将字符型数据做因子化处理,将其转换为整数型数据columns = mushrooms.columns[1:] for column in columns:mushrooms[column] = pd.factorize(mushrooms[column])[0] mushrooms.head()见表10-4。
如表10-4所示,所有的字符型变量全部转换成了数值,而且每一列中的数值都代表了各自不同的字符值。需要注意的是,factorize函数返回的是两个元素的元组,第一个元素为转换成的数值,第二个元素为数值对应的字符水平,所以在类型转换时,需要通过索引方式返回因子化的值。接着就可以使用多项式贝叶斯分类器对如上数据集进行类别的预测,为了实现模型的验证,需要将该数据集拆分为训练集和测试集,代码如下:
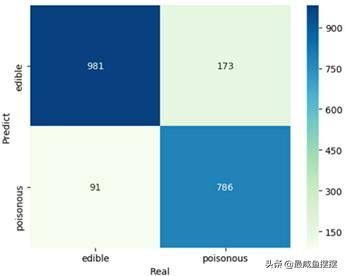
见图10-3。
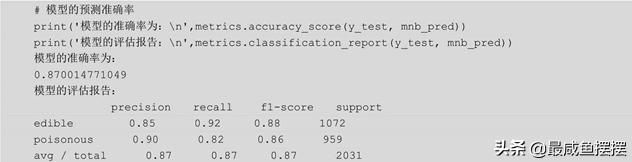
在如上的混淆矩阵图中,横坐标代表测试数据集中的实际类别值, 纵坐标为预测类别值,正确预测无毒的有981个样本,正确预测有毒的有786个样本。基于混淆矩阵的进一步运算,可以得到如上所示的两部分结果,并从中发现,模型在测试数据集上的整体预测准确率为87%, 而且从各类别值来看,无毒蘑菇的预测覆盖率为92%、有毒蘑菇的预测覆盖率为82%。总体来说,模型的预测效果还是非常理想的,接下来继续绘制ROC曲线,查看对应的AUC值的大小,代码如下:
见图10-4。
如图10-4所示,ROC曲线下的面积为0.94,超过阈值0.8,可以认为模型的效果是可以接受的。需要注意的是,当因变量为字符型的值时, 子模块metrics中的函数roc_curve必须传入数值型的因变量(如代码所 示,将字符值和数值做了映射),否则会报错误信息。对于离散型自变量的数据集而言,在分类问题上并非都可以使用多项式贝叶斯分类器,如果自变量在特定y值下的概率不服从多项式分布的话,分类器的预测效果就不会很理想。通常情况下,会利用多项式贝叶斯分类器作文本分类,如一份邮件是否垃圾邮件、用户评论是否为正面等。
10.2.5 伯努利贝叶斯分类器
当数据集中的自变量X均为0-1二元值时(例如在文本挖掘中,判断某个词语是否出现在句子中,出现用1表示,不出现用0表示),通常会优先选择伯努利贝叶斯分类器。利用该分类器计算概率值P(X|Ci)时,会假设自变量X的条件概率满足伯努利分布,故概率值P(X|Ci)的计算公式可以表示为:
P(xj|Ci)=pxj+(1-p) (1-xj)
其中,xj为第j个自变量,取值为0或1;p表示类别为Ci时自变量取1 的概率,该概率值可以使用经验频率代替,即
其中,Ni表示类别Ci的样本个数;Nxj表示在类别为Ci时,xj变量取1 的样本量;α为平滑系数,同样是为了避免概率为0而设置的;n为因变量中的类别个数。
下面举一个通俗易懂的例子,并通过手工计算的方式来说明伯努利贝叶斯分类器在文本分类中的应用。
假设对10条评论数据做分词处理后,得到如表10-5所示的文档词条矩阵,矩阵中含有5个词语和1个表示情感的结果,其中类别为0表示正面情绪,1表示负面情绪。如果一个用户的评论中仅包含“还行”一词, 请问该用户的评论属于哪种情绪?接下来通过手动的方式,计算该用户的评论属于正面和负面的概率,步骤如下:
(1) 因变量各类别频率
P(类别=0)=4/10=2/5 P(类别=1)=6/10=3/5
(2) 单变量条件概率
P(x1=0|类别=0)=(1+1)/(4+2)=1/3 P(x1=0|类别=1)=(4+1)/(6+2)=5/8 P(x2=0|类别=0)=(1+1)/(4+2)=1/3 P(x2=0|类别=1)=(4+1)/(6+2)=5/8 P(x3=0|类别=0)=(4+1)/(4+2)=5/6 P(x3=0|类别=1)=(1+1)/(6+2)=1/4 P(x4=1|类别=0)=(2+1)/(4+2)=1/2
P(x4=1|类别=1)=(0+1)/(6+2)=1/8 P(x5=0|类别=0)=(4+1)/(4+2)=5/6 P(x5=0|类别=1)=(1+1)/(6+2)=1/4
(3) 贝叶斯后验概率
如上结果所示,当用户的评论中只含有“还行”一词时,计算该评论为正面情绪的概率约为0.015,评论为负面情绪的概率约为0.00073,故根据贝叶斯后验概率最大原则将该评论预判为正面情绪。
伯努利贝叶斯分类器的计算与多项式贝叶斯分类器的计算非常相 似,在文本分类问题中,如果构造的数据集是关于词语出现的次数,通常会选择多项式贝叶斯分类器进行预测;如果构造的数据集是关于词语是否会出现的0-1值,则会选择伯努利贝叶斯分类器进行预测。当读者需要构造伯努利贝叶斯分类器时,可以直接调用sklearn子模块naive_bayes中的BernoulliNB类。有关该“类”的语法和参数含义如下:
BernoulliNB (alpha = 1.0, binarize=0.0, fit_prior = True, clalpha:用于指定平滑系数α的值,默认为1.0。
binarize:如果该参数为浮点型数值,则将以该值为界限,当自变量的值大于该值时,自变量的值将被转换为1,否则被转换为0;如果该参数为None时,则默认训练数据集的自变量均为0-1 值。
fit_prior:bool类型参数,是否以数据集中各类别的比例作为P(Ci)的先验概率,默认为True。
class_prior:用于人工指定各类别的先验概率P(Ci),如果指定该参数,则参数fit_prior不再有效。
接下来将利用Python中的BernoulliNB类对用户的评价数据进行分 类,分类的目的是预测用户的评价内容所表达的情绪(积极或消极)。
10.2.6 伯努利贝叶斯分类器的应用
用户对其购买的蚊帐进行评论,该数据集是通过爬虫的方式获得, 一共包含10 644条评论,数据集中的Type变量为评论所对应的情绪。首先将爬虫获得的数据集读入Python中,并预览前几行数据,代码如下:
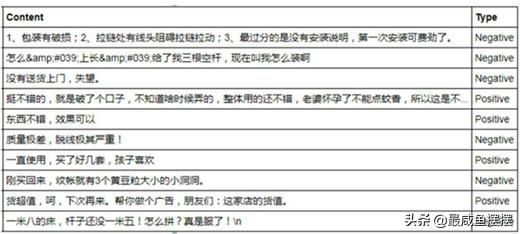
# 读入评论数据evaluation = pd.read_excel(r'C:甥敳獲AdministratorDesktop # 查看数据前10行,见表10-6evaluation.head(10)如表10-6所示,数据集包含4个字段,分别是用户昵称、评价时间、评价内容和对应的评价情绪。从评价内容来看,会有一些“脏”文本在内,如数字、英文等,所以需要将这些“脏”文本删除,代码如下:
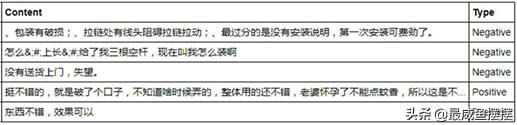
# 运用正则表达式,将评论中的数字和英文去除evaluation.Content = evaluation.Content.str.replace('[0-9a-z evaluation.head()见表10-7。
经过数据的初步清洗后,下一步要做的就是对文本进行切词,但在切词前,通常需要引入用户自定义的词库和停止词。利用词典的目的是将无法正常切割的词实现正确切割(如“沙瑞金书记”会被切词为“沙”“瑞金”“书记”,为了避免这种情况,就需要将类似“沙瑞金”这样的词组合为词库),使用停止词的目的是将句子中无意义的词语删除(如“的”“啊”“我们”等)。
如上结果所示,通过调入第三方包jieba实现中文的切词,并在切词过程中加入自定义词库和删除停止词。接下来利用如上的切词结果,构造文档词条矩阵,矩阵的每一行代表一个评论内容,矩阵的每一列代表切词后的词语,矩阵的元素为词语在文档中出现的频次。代码如下:
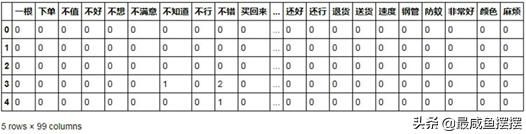
见表10-8。
如表10-8所示,将文档词条矩阵转换为数据框后得到一个庞大的稀疏矩阵,即数据框中的大部分值为0。为了避免数据框的列数过多,在构造文档词条矩阵时做了相应的限制条件,即代码中的CountVectorizer(min_df = 0.01),表示词语所对应的文档数目必须在所有文档中至少占1%的比例,最终得到表10-8中所呈现的99个变量。有了如上的数据框,接下来要做的就是将数据集拆分为训练集和测试集,并利用训练集构建伯努利贝叶斯分类器,利用测试集对分类器的预测效果进行评估,具体代码如下:
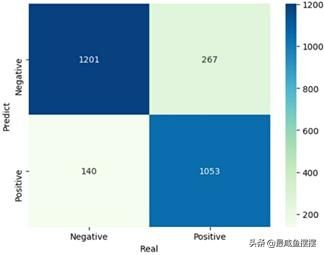
见图10-5。
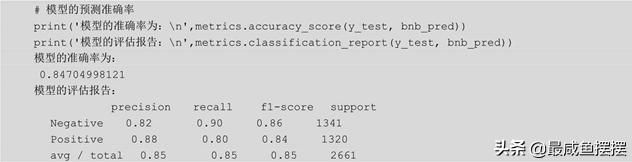
如上结果所示,从混淆矩阵图形来看,伯努利贝叶斯分类器在预测数据集上的效果还是非常棒的,绝大多数的样本都被预测正确(因为主对角线上的数据非常大),而且总的预测准确率接近85%;从模型的评估报告来看,预测为消极情绪的覆盖率0.9相比于积极情绪的覆盖率0.8 要更高一些,但总体来说模型的预测效果还是不错的。同理,再绘制一下关于模型在测试数据集上的ROC曲线,代码如下:
见图10-6。
如图10-6所示,绘制的ROC曲线所对应的AUC值为0.93,同样是一个非常高的数值,再结合模型准确率、覆盖率等指标,可以认为该模型在测试数据集上的预测效果是非常理想的。需要说明的是,如果训练数据集是关于词语在各文档中出现的频次,直接调用BernoulliNB类是没有问题的,因为该“类”中参数binarize默认值为0,即如果词的频次大于0,则对应的变量值在模型运算时会转换成1,否则转换为0。
10.3 本章小结
本章介绍了有关三种朴素贝叶斯分类器,这三种分类器的选择主要依赖于自变量X数据的类型。如果自变量X均为连续的数值型,则需要选择高斯贝叶斯分类器;如果自变量X均表示为离散的数据类型,则需要选择多项式贝叶斯分类器;如果自变量X为0-1二元值,则需要选择伯努利贝叶斯分类器。朴素贝叶斯分类器的核心假设为自变量之间是条件独立的,该假设的主要目的是为了提高算法的运算效率,如果实际数据集中的自变量不满足独立性假设时,分类器的预测结果往往会产生错 误。
本章的主要内容包含了三种朴素贝叶斯分类器的理论思想、运算过程和应用实战,通过本章内容的学习,读者可以对比三者的差异和应用场景,并从中选择合理的是算法完成工作中的实际需求。
为了使读者掌握有关本章内容所涉及的函数和“方法”,这里将其重新梳理一下,以便读者查阅和记忆。