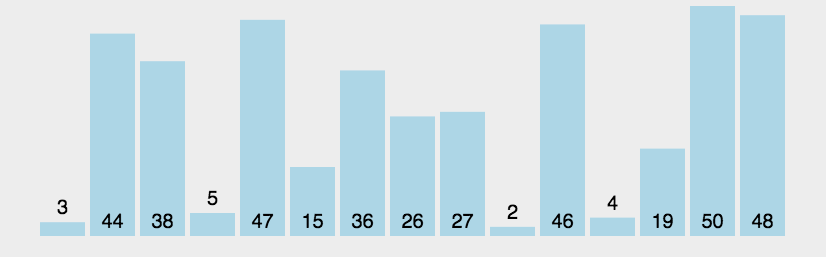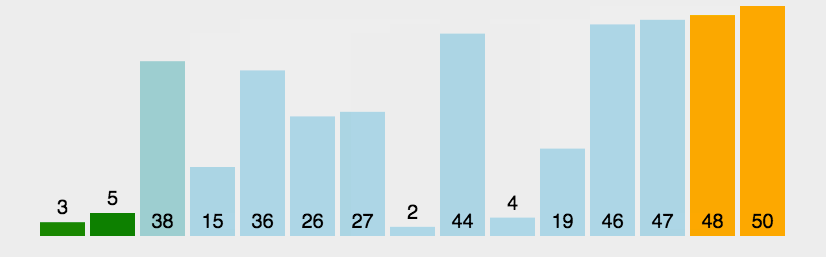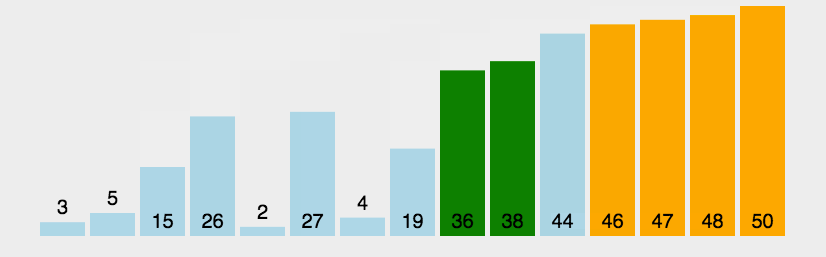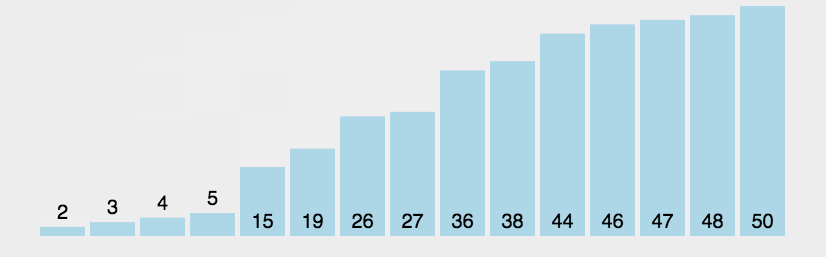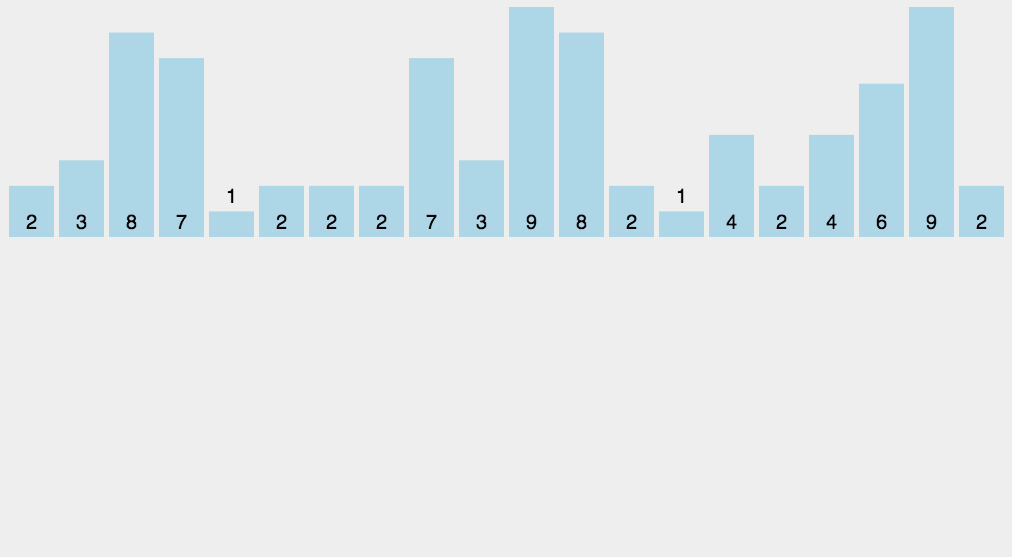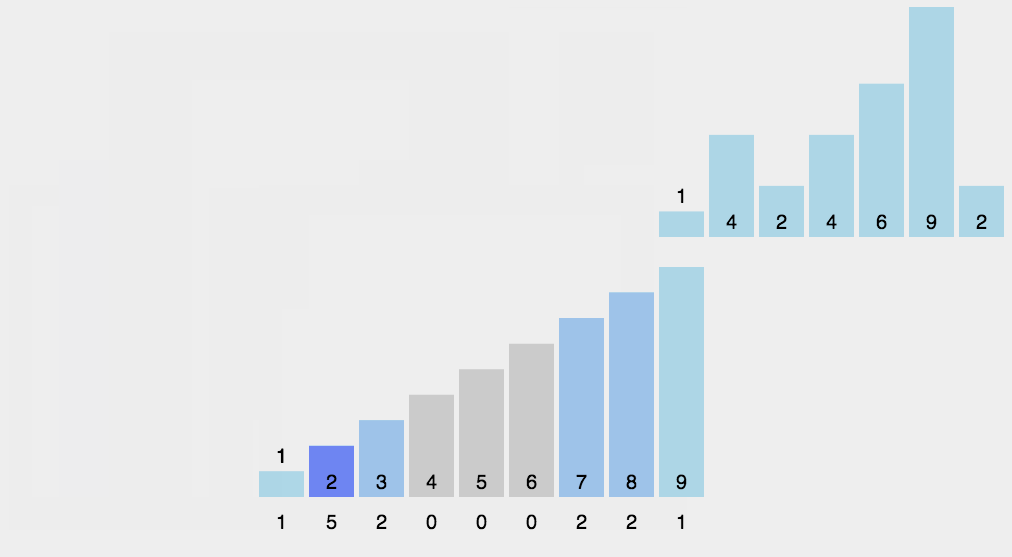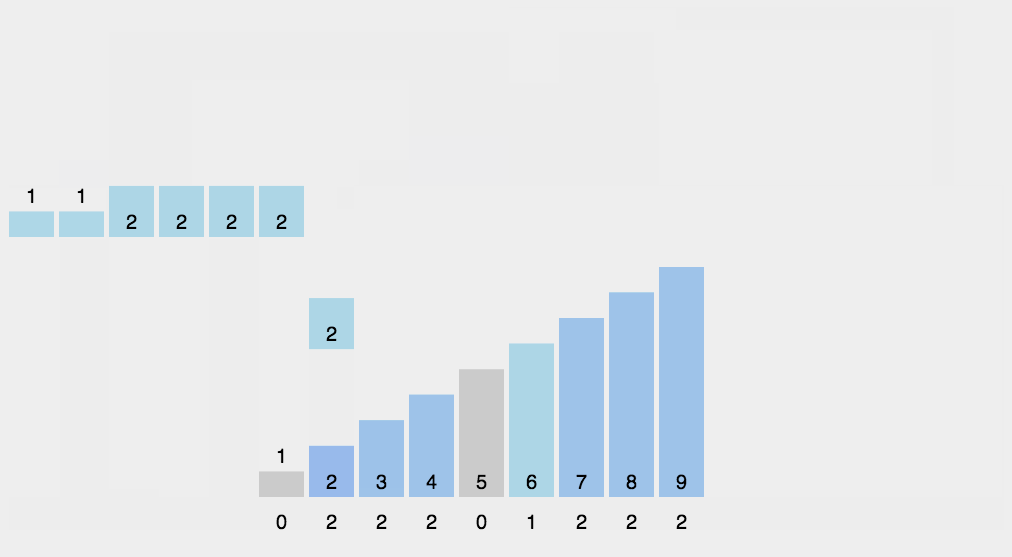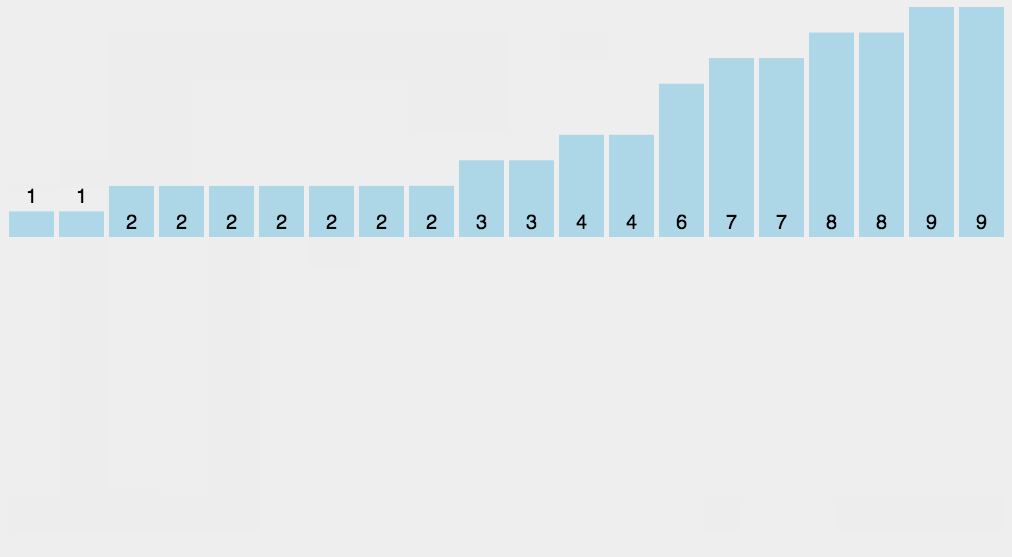排序算法归纳以及其实现:冒泡排序,选择排序,插入排序,希尔排序,堆排序,归并排序,快速排序,桶排序,计数排序, 基数排序
文章目录
- 冒泡排序(Bubble Sort)
-
- 原理说明
- 动图演示
- Java代码实现
- 选择排序(Selection Sort)
-
- 原理说明
- 动图演示
- Java代码实现
- 插入排序(Insertion Sort)
-
- 动图演示
- Java代码实现
- 希尔排序(Shell Sort)
-
- 动图演示
- Java代码实现
- 堆排序(Heap Sort)
-
- 原理说明
- Java代码实现
- 归并排序(Merge Sort)
-
- 原理说明
- 动图演示
- 归并排序伪代码
- Java代码实现
- 快速排序(Quick Sort)【重要】
-
- 原理说明
- 快排和归并排序的比较
- 动图演示
- 快排伪代码
- Java代码实现
- 桶排序(Bucket Sort)
-
- 原理说明
- 计数排序(Counting Sort)
-
- 原理说明
- 动图演示
- Java代码实现
- 基数排序(Padix Sort)
-
- 原理说明
- 动图演示
- 参考
冒泡排序(Bubble Sort)
原理说明
重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。遍历数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的最右端。
动图演示
Java代码实现
package sort;
/**
* 冒泡排序Java实现
*
* @author ZhaoSimon
*/
public class BubbleSort {
public static void bubbleSort(int[] nums, int length) {
if (length <= 1) {
return;
}
for (int i = 0; i < length - 1; ++i) {
/*
j不用每次都从0开始遍历到 n-2 的位置结束,
第一次遍历结束,第一大的元素被排在了倒数第一的位置,
第二次遍历结束,第二大的元素将会被放到导数第二的位置,因此此时就只用遍历到 n-3 的位置即可
*/
for (int j = 0; j < length - 1 - i; ++j) {
if (nums[j] > nums[j + 1]) {
int tmp = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = tmp;
}
}
}
}
}
选择排序(Selection Sort)
原理说明
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕
动图演示
Java代码实现
package sort;
/**
* 选择排序Java实现
* @author ZhaoSimon
*/
public class SelectionSort {
public static void selectionSort(int[] nums, int length) {
if (length <= 1) {
return;
}
for (int i = 0; i < length; ++i) {
int minIndex = i;
for (int j = i; j < length; ++j) {
if (nums[j] < nums[minIndex]) {
minIndex = j;
}
}
int tmp = nums[minIndex];
nums[minIndex] = nums[i];
nums[i] = tmp;
}
}
}
插入排序(Insertion Sort)
动图演示
Java代码实现
通过交换元素来达到插入的目的。
package sort;
/**
*
* 插入排序Java实现
* 调用insertSort(int[] nums, int length)实现插入排序
* @author ZhaoSimon
*/
public class InsertionSort {
public static void insertSort(int[] nums, int length) {
if (length <= 1) {
return;
}
for (int cur = 1; cur < length; ++cur) {
int j = cur;
while (j > 0 && nums[j - 1] > nums[j]) {
swap(nums, j, j - 1);
--j;
}
}
}
private static void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}
希尔排序(Shell Sort)
动图演示
Java代码实现
package sort;
/**
* 希尔排序Java实现
* 调用shellSort(int[] nums, int length)实现希尔排序
* @author ZhaoSimon
*/
public class ShellSort {
public static void shellSort(int[] nums, int length) {
if (length <= 1) {
return;
}
for (int gap = length / 2; gap > 0; gap /= 2) {
insertSortWithGap(nums, nums.length, gap);
}
}
/**
*
* @param nums 待排序数组
* @param length 待排序数组的长度
* @param gap 间隔
*/
private static void insertSortWithGap(int[] nums, int length, int gap) {
for (int cur = gap; cur < length; ++cur) {
int j = cur;
while (j - gap >= 0 && nums[j - gap] > nums[j]) {
swap(nums, j, j - gap);
j -= gap;
}
}
}
private static void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}
堆排序(Heap Sort)
原理说明
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
Java代码实现
利用Java的Priority Queue来实现大顶堆。
package sort;
import java.util.PriorityQueue;
/**
* compare(Integer o1, Integer o2) { return o1 - o2;}说明:
* 如果是return o1 - o2;那么当o1大于o2时,o1 - o2 > 0,return一个正数则表示o1 > o2
* 但是若return o2 - o1;同样是o1大于o2,但是由于o2 - o1 < 0,则会return一个负数,程序则会认为o1 < o2,排序就会颠倒,达到逆序排列的目的
* 若函数return 0则表示o1 == o2
*
* 利用PriorityQueue实现堆排序
* @author ZhaoSimon
*
*/
public class HeapSort {
public static void heapSort(int[] nums, int length) {
if (length <= 1) {
return;
}
//PriorityQueue默认是小顶堆,如果是要实现大顶堆,则需要重写Comparator接口
PriorityQueue<Integer> minHeap = new PriorityQueue<>(length);
//方法一:使用匿名内部类
// PriorityQueue maxHeap = new PriorityQueue<>(length, new Comparator() {
// @Override
// public int compare(Integer o1, Integer o2) {
// return o2 - o1;
// }
// });
//方法二:使用Lamda表达式
// PriorityQueue maxHeap = new PriorityQueue<>(length, (o1, o2) -> o2 - o1);
for (int tmp : nums) {
minHeap.add(tmp);
}
for (int i = 0; i < length; ++i) {
nums[i] = minHeap.poll();
}
}
}
归并排序(Merge Sort)
原理说明
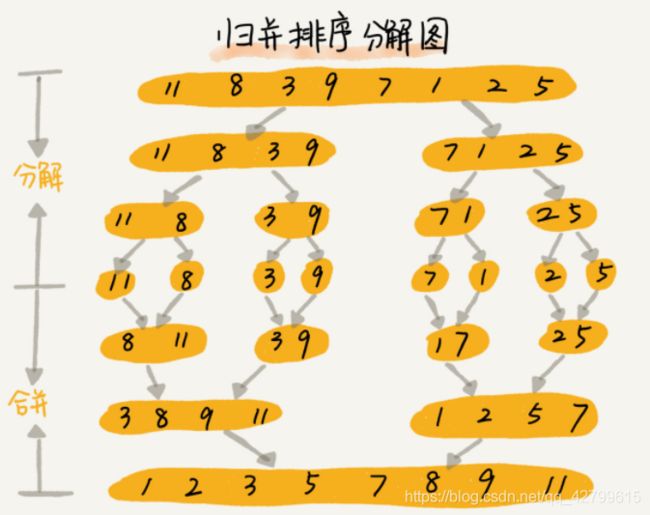
如果要排序一个数组,我们先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两部分合并在一起,这样整个数组就都有序了。
动图演示
归并排序伪代码
// 归并排序算法, A是数组,n表示数组大小
merge_sort(A, n) {
merge_sort_c(A, 0, n-1)
}
// 递归调用函数
merge_sort_c(A, p, r) {
// 递归终止条件
if p >= r then return
// 取p到r之间的中间位置q
q = (p+r) / 2
// 分治递归
merge_sort_c(A, p, q)
merge_sort_c(A, q+1, r)
// 将A[p...q]和A[q+1...r]合并为A[p...r]
merge(A[p...r], A[p...q], A[q+1...r])
}
Java代码实现
package sort;
/**
* 归并排序Java实现
* 调用mergeSort(int[] nums, int length)实现归并排序
* @author ZhaoSimon
*/
public class MergeSort {
public static void mergeSort(int[] nums, int length) {
if (length <= 1) {
return;
}
mergeSort(nums, 0, length - 1);
}
private static void mergeSort(int[] nums, int start, int end) {
if (start >= end) {
return;
}
int p = (start + end) / 2;
//不断将数组划分成小区间
mergeSort(nums, start, p);
mergeSort(nums, p + 1, end);
merge(nums, start, p, p + 1, end);
}
/**
*
* @param nums 操作的数组
* @param start1 第一部分待合并数组的起始下标
* @param end1 第一部分待合并数组的终止下标
* @param start2 第二部分待合并数组的起始下标
* @param end2 第二部分待合并数组的起始下标
*/
private static void merge(int[] nums, int start1, int end1, int start2, int end2) {
int[] tmpArray = new int[end2 - start1 + 1];
int i = start1, j = start2, k = 0;
while (i <= end1 && j <= end2) {
if (nums[i] <= nums[j]) {
tmpArray[k++] = nums[i++];
} else {
tmpArray[k++] = nums[j++];
}
}
while (i <= end1) {
tmpArray[k++] = nums[i++];
}
while (j <= end2) {
tmpArray[k++] = nums[j++];
}
k = 0;
for (int m = start1; m <= end2; ++m) {
nums[m] = tmpArray[k++];
}
}
}
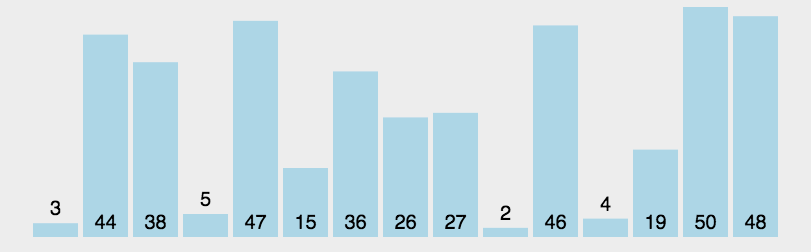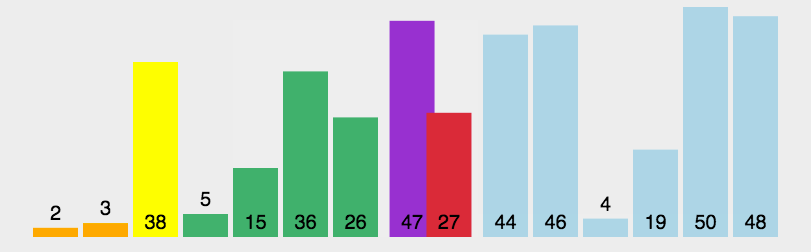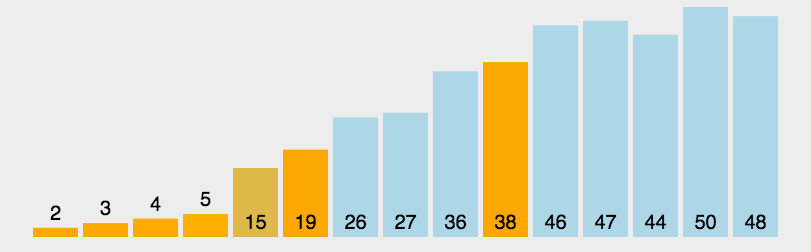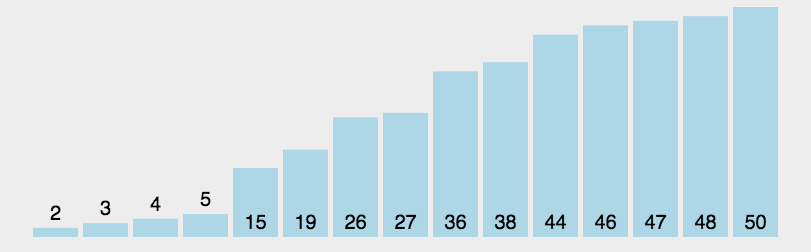
快速排序(Quick Sort)【重要】
原理说明
如果要排序数组中下标从 p 到 r 之间的一组数据,我们选择 p 到 r 之间的任意一个数据作为 pivot(分区点)。我们遍历 p 到 r 之间的数据,将小于 pivot 的放到左边,将大于 pivot 的放到右边,将 pivot 放到中间。经过这一步骤之后,数组 p 到 r 之间的数据就被分成了三个部分,前面 p 到 q-1 之间都是小于 pivot 的,中间是 pivot,后面的 q+1 到 r 之间是大于 pivot 的。
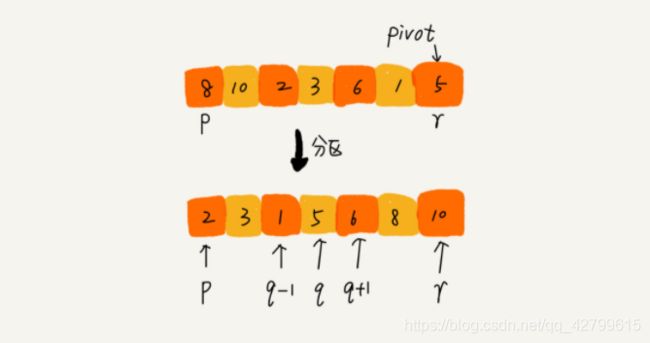
分区的整个过程:
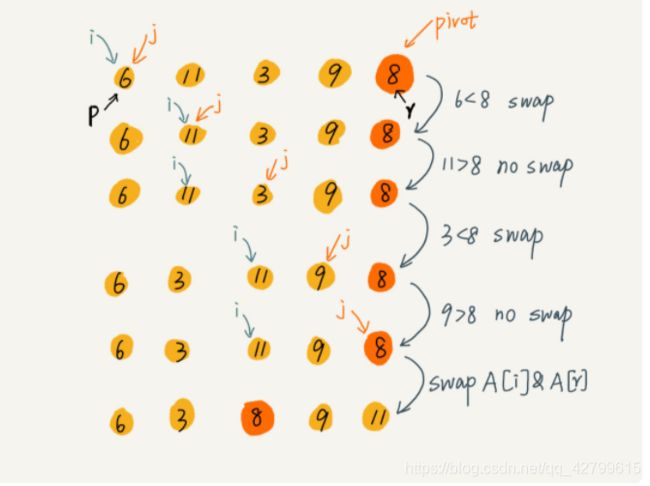
- 快排不是稳定的排序算法
快排和归并排序的比较
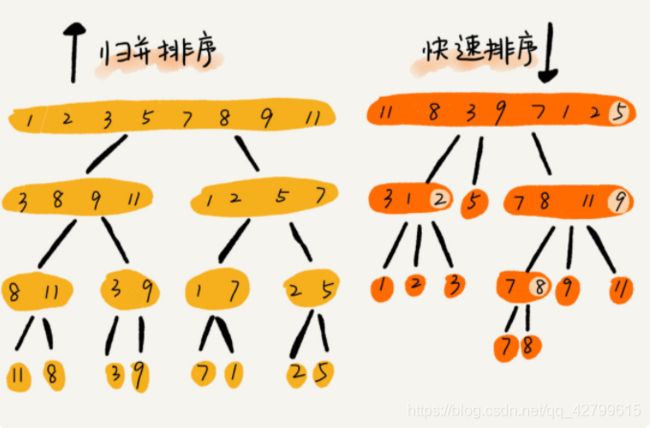
归并排序的处理过程是由下到上的,先处理子问题,然后再合并。而快排正好相反,它的处理过程是由上到下的,先分区,然后再处理子问题。归并排序虽然是稳定的、时间复杂度为 O(nlogn) 的排序算法,但是它是非原地排序算法。我们前面讲过,归并之所以是非原地排序算法,主要原因是合并函数无法在原地执行。快速排序通过设计巧妙的原地分区函数,可以实现原地排序,解决了归并排序占用太多内存的问题。
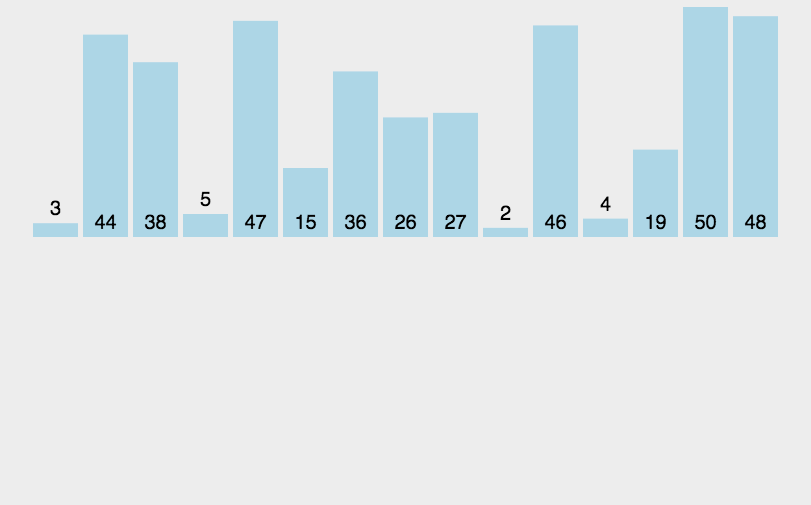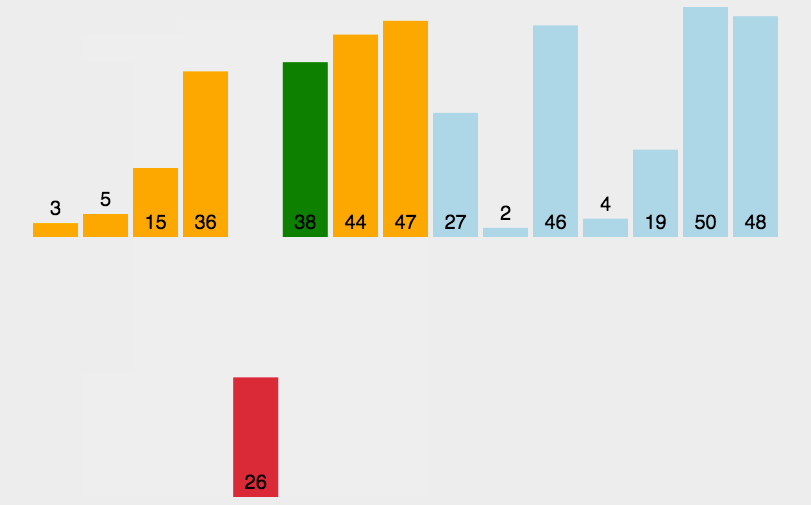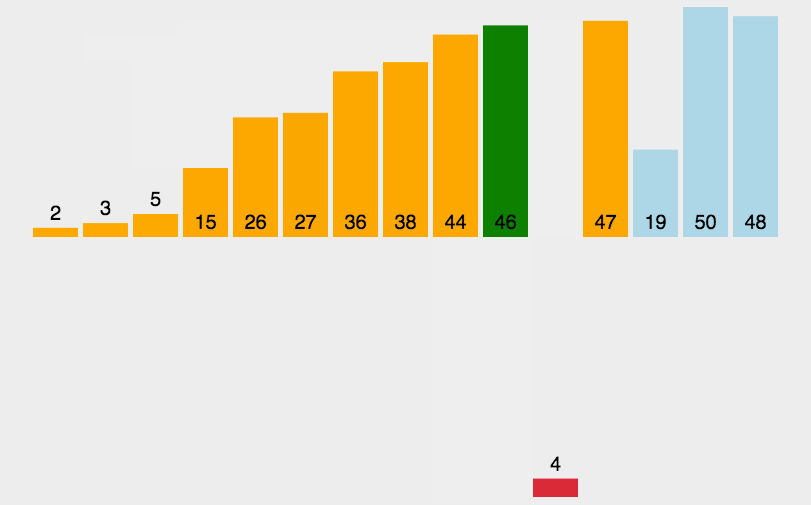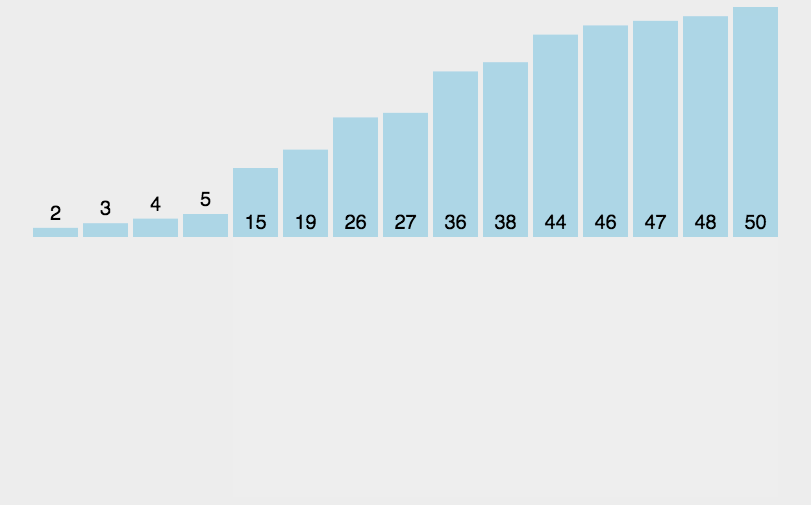
动图演示
快排伪代码
// 快速排序,A是数组,n表示数组的大小
quick_sort(A, n) {
quick_sort_c(A, 0, n-1)
}
// 快速排序递归函数,p,r为下标
quick_sort_c(A, p, r) {
if p >= r then return
q = partition(A, p, r) // 获取分区点
quick_sort_c(A, p, q-1)
quick_sort_c(A, q+1, r)
}
Java代码实现
package sort;
/**
* 快排Java实现
* 调用quickSort(int[] nums, int length)实现快速排序
*
* @author ZhaoSimon
*/
public class QuickSort {
/**
* @param nums 待排序的数组
* @param length 待排序数组的长度
*/
public static void quickSort(int[] nums, int length) {
if (length <= 1) {
return;
}
quickSort(nums, 0, length - 1);
}
/**
* @param nums 待排序的数组
* @param start 数组中待排序元素的起始下标
* @param end 数组中待排序元素的结束下标
*/
private static void quickSort(int[] nums, int start, int end) {
if (start >= end) {
return;
}
int q = parttion(nums, start, end);
quickSort(nums, 0, q - 1);
quickSort(nums, q + 1, end);
}
private static int parttion(int[] nums, int start, int end) {
int privot = end;
int i = start, j;
for (j = start; j < end; ++j) {
if (nums[j] < nums[privot]) {
swap(nums, i, j);
++i;
}
}
swap(nums, i, privot);
privot = i;
return privot;
}
private static void swap(int[] nums, int i, int j) {
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}
桶排序(Bucket Sort)
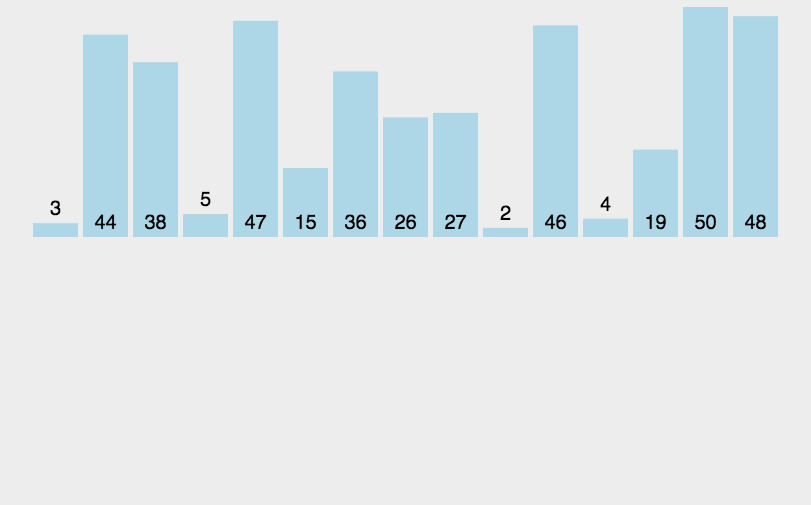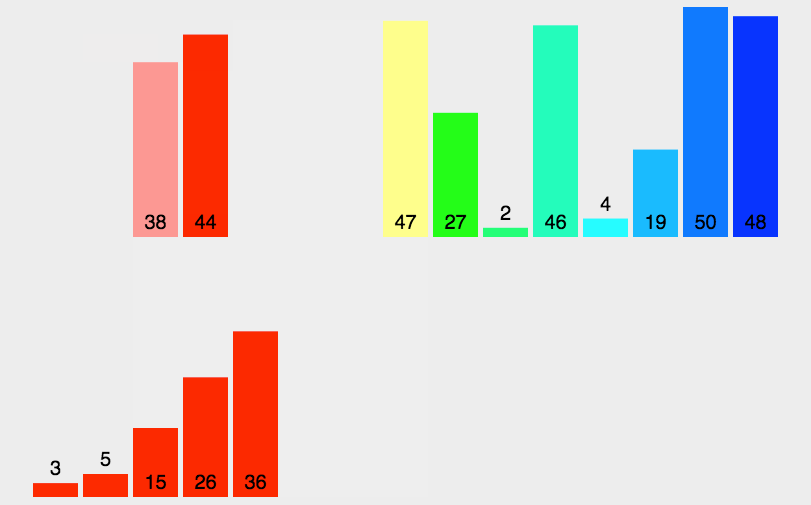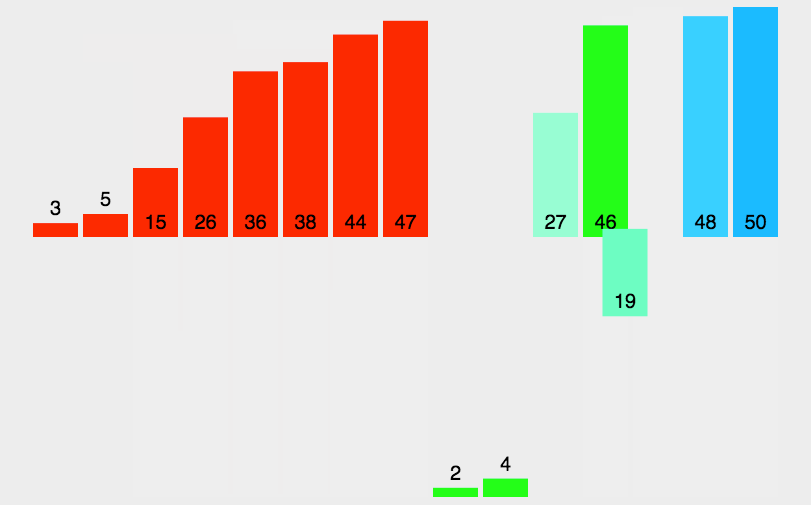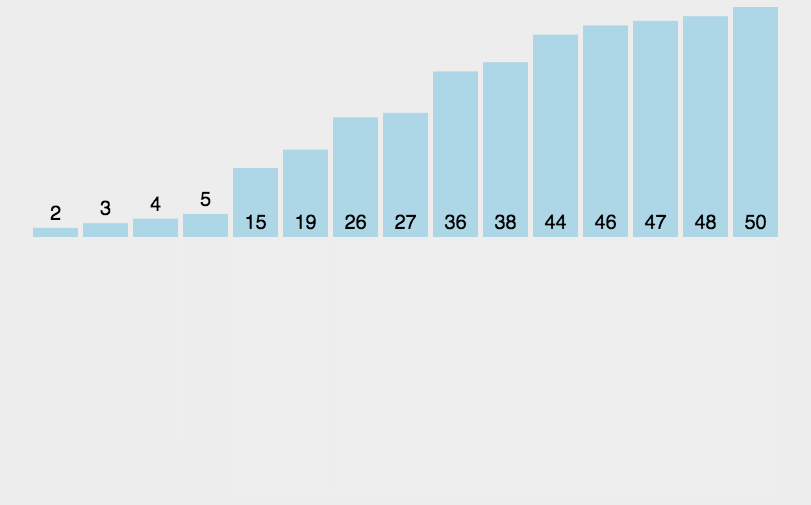
原理说明
桶排序的核心思想是将要排序的数据分到几个有序的桶里,每个桶里的数据再单独进行排序。桶内排完序之后,再把每个桶里的数据按照顺序依次取出,组成的序列就是有序的了。

桶排序的时间复杂度为什么是 O(n) 呢?
如果要排序的数据有 n 个,我们把它们均匀地划分到 m 个桶内,每个桶里就有 k=n/m 个元素。每个桶内部使用快速排序,时间复杂度为 O(k * logk)。m 个桶排序的时间复杂度就是 O(m * k * logk),因为 k=n/m,所以整个桶排序的时间复杂度就是 O(n*log(n/m))。当桶的个数 m 接近数据个数 n 时,log(n/m) 就是一个非常小的常量,这个时候桶排序的时间复杂度接近 O(n)
桶排序的限制
- 首先,要排序的数据需要很容易就能划分成 m 个桶,并且,桶与桶之间有着天然的大小顺序。这样每个桶内的数据都排序完之后,桶与桶之间的数据不需要再进行排序。
- 其次,数据在各个桶之间的分布是比较均匀的。如果数据经过桶的划分之后,有些桶里的数据非常多,有些非常少,很不平均,那桶内数据排序的时间复杂度就不是常量级了。在极端情况下,如果数据都被划分到一个桶里,那就退化为 O(nlogn) 的排序算法了。
- 最后,桶排序比较适合用在外部排序中。所谓的外部排序就是数据存储在外部磁盘中,数据量比较大,内存有限,无法将数据全部加载到内存中
计数排序(Counting Sort)
原理说明
我们都经历过高考,高考查分数系统你还记得吗?我们查分数的时候,系统会显示我们的成绩以及所在省的排名。如果你所在的省有 50 万考生,如何通过成绩快速排序得出名次呢?
考生的满分是 900 分,最小是 0 分,这个数据的范围很小,所以我们可以分成 901 个桶,对应分数从 0 分到 900 分。根据考生的成绩,我们将这 50 万考生划分到这 901 个桶里。桶内的数据都是分数相同的考生,所以并不需要再进行排序。我们只需要依次扫描每个桶,将桶内的考生依次输出到一个数组中,就实现了 50 万考生的排序。因为只涉及扫描遍历操作,所以时间复杂度是 O(n)。
计数排序只能用在数据范围不大的场景中,如果数据范围 k 比要排序的数据量n 大很多,就不适合用计数排序了。而且,计数排序只能给非负整数排序,如果要排序的数据是其他类型的,要将其在不改变相对大小的情况下,转化为非负整数。
动图演示
Java代码实现
package sort;
public class CountingSort {
public static void countingSort(int[] nums, int length) {
if (length <= 1) {
return;
}
//找出数组中的最大值,最大值决定了数组的大小
int max = Integer.MIN_VALUE;
for (int tmp : nums) {
max = Math.max(tmp, max);
}
//数组元素初始化后默认为0
int[] count = new int[max + 1];
for (int tmp : nums) {
count[tmp]++;
}
//统计nums中每个数值出现的次数
for (int i = 1; i < count.length; ++i) {
count[i] += count[i - 1];
}
//用临时数组来存储有序的元素
int[] tmpArray = new int[length];
for (int j = length - 1; j >= 0; --j) {
int index = count[nums[j]] - 1;
tmpArray[index] = nums[j];
count[nums[j]]--;
}
for (int k = 0; k < nums.length; ++k) {
nums[k] = tmpArray[k];
}
}
}
基数排序(Padix Sort)
原理说明
假设我们有 10 万个手机号码,希望将这 10 万个手机号码从小到大排序,你有什么比较快速的排序方法呢?
处理思路:先按照最后一位来排序手机号码,然后,再按照倒数第二位重新排序,以此类推,最后按照第一位重新排序。经过 11 次排序之后,手机号码就都有序了。
这便是基数排序
基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。
基数排序对要排序的数据是有要求的,需要可以分割出独立的“位”来比较,而且位之间有递进的关系,如果 a 数据的高位比 b 数据大,那剩下的低位就不用比较了。除此之外,每一位的数据范围不能太大,要可以用线性排序算法来排序,否则,基数排序的时间复杂度就无法做到 O(n) 了
动图演示
参考
- 十大经典排序算法
- 排序(下):如何用快排思想在O(n)内查找第K大元素
- 线性排序:如何根据年龄给100万用户数据排序?