基于线性模型的异常检测

一、概述

真实数据集的不同维度之间具有高度的相关性。这是因为不同的属性通常由相同的底层流程以密切相关的方式生成。在经典统计文献中，这被称为回归建模。一些形式的相关分析试图从其他方面预测个体属性值，而另一种形式则以潜在变量的形式总结整个数据。后者的一个例子是主成分分析方法。这两种建模形式在离群值分析的不同场景中都非常有用。
线性模型的主要假设是数据被嵌入到一个低维子空间中，在线性方法中，目标是找到低维子空间，其中离群点的行为与其他点非常不同。
在本文中，我们将主要研究两类线性模型，第一类模型使用因变量和自变量之间的统计回归建模，以确定数据中特定种类的依赖关系。第二类模型主要采用主成分分析对所有属性进行齐次处理，确定投影的低维子空间。

二、 基本线性回归模型

在线性回归中，数据中的观测值是用一个线性方程组建模的。具体来说，数据中的不同维度使用一组线性系数相关联。回归分析通常被认为是统计学中的一个重要应用。在此应用程序中的经典实例化中，人们希望从一组自变量中学习特定的因变量。
在这种情况下，异常值是根据其他自变量对因变量的影响来定义的，而自变量之间相互关系中的异常则不那么重要。这里的异常点检测主要用于数据降噪，避免异常点的出现对模型性能的影响，因而这里关注的兴趣点主要是正常值(n)。

基于自变量与因变量的线性回归

最小二乘法

为了简单起见，这里我们一元线性回归为例:

$$Y=\sum _{i=1}^d{a}_i\cdot X_i+a_{d+1}$$
  
  变量Y为因变量，也就是我们要预测的值；$X_1...X_d$为一系列因变量，也就是输入值。系数$a_1...a_{d+1}$为要学习的参数。假设数据共包含$N$个样本，第$j$个样本包含的数据为$x_{j1}...x_{jd}$和$y_j$，带入式(1)如下式所示：

$$y_j=\sum _{i=1}^d{a}_i\cdot x_{ji}+a_{d+1}+{ϵ}_j$$

  这里${ϵ}_j$为第$j$个样本的误差。以$Y$ 代表 $N\times 1$ 的因变量矩阵${(y_1...y_N)}^T$，即样本中的真实值；以$U$代表$N\times (d+1)$的自变量矩阵，其中第$j$行为$(x_{j1}...x_{jd},1)$；以$A$ 代表 $(d+1)\times 1$ 的系数矩阵$(a_1...a_{d+1}{)}^T$。则模型可表示为：
$$f(U,A)=U\cdot A$$

  定义目标函数为：

$$L(A)=\frac{1}{2}{\Vert Y-U\cdot A\Vert }^2$$

  目标函数是关于$A$的凸函数，其对$A$求偏导为：

$$\frac{\partial L(A)}{\partial A}=\frac{1}{2}\frac{\partial {\Vert Y-U\cdot A\Vert }^2}{\partial A}=-U^T(Y-U\cdot A)$$

  令$\frac{\partial L(A)}{\partial A}=0$，得到最优参数为：

$$A={\left(U^T\cdot U\right)}^{-1}\cdot \left(U^T\cdot Y\right)$$

  这种求解线性回归参数的方法也叫最小二乘法。

2.1.2 梯度下降法

数据集

  监督学习一般靠数据驱动。我们通常收集一系列的真实数据，例如多栋房屋的真实售出价格和它们对应的面积和房龄。我们希望在这个数据上面寻找模型参数来使模型的预测价格与真实价格的误差最小。在机器学习术语里，该数据集被称为训练数据集（training data set）或训练集（training set），通常还应该有一个用于防止过拟合的交叉验证集和一个用于评估模型性能的测试集(test set)。一栋房屋被称为一个样本（sample），其真实售出价格叫作标签（label），用来预测标签的两个因素叫作特征（feature）。

损失函数

  如果把线性回归看作是一个优化问题，那么我们要优化的目标就是损失函数。损失函数是用来衡量样本误差的函数，我们的优化目标是要求得在误差最小的情况下模型参数的值。这里强调一下损失函数和代价函数的区别：

注意：
**Loss Function(损失函数)：**the error for single training example;
**Cost Function(代价函数)：**the average of the loss functions of the entire training set;

  线性回归常用的损失函数是均方误差，表达式为：

$$l^{(i)}(\mathbf{w},b)=\frac{1}{2}{\left({\hat{y}}^{(i)}-y^{(i)}\right)}^2$$

$$L(\mathbf{w},b)=\frac{1}{n}\sum _{i=1}^n{l}^{(i)}(\mathbf{w},b)=\frac{1}{n}\sum _{i=1}^n\frac{1}{2}{\left({\mathbf{w}}^{\top }{\mathbf{x}}^{(i)}+b-y^{(i)}\right)}^2$$
  其中 $\hat{y}$ 为预测值，$y$ 为真实值。
优化算法 - 随机梯度下降

  当模型和损失函数形式较为简单时，上面的误差最小化问题的解可以直接用公式表达出来。这类解叫作解析解（analytical solution）。本节使用的线性回归和平方误差刚好属于这个范畴。然而，大多数深度学习模型并没有解析解，只能通过优化算法有限次迭代模型参数来尽可能降低损失函数的值。这类解叫作数值解（numerical solution）。

  在求数值解的优化算法中，小批量随机梯度下降（mini-batch stochastic gradient descent）被广泛使用。它的算法很简单：先选取一组模型参数的初始值，如随机选取；接下来对参数进行多次迭代，使每次迭代都可能降低损失函数的值。在每次迭代中，先随机均匀采样一个由固定数目训练数据样本所组成的小批量（mini-batch），然后求小批量中数据样本的平均损失和有关模型参数的导数（梯度），最后用此结果与预先设定的学习率的乘积作为模型参数在本次迭代的减小量。如下式所示：

$$(\mathbf{w},b)\leftarrow (\mathbf{w},b)-\frac{\eta }{|\mathcal{B}|}\sum _{i\in \mathcal{B}}{\partial }_{(\mathbf{w},b)}{l}^{(i)}(\mathbf{w},b)$$

学习率($\eta$): 代表在每次优化中，能够学习的步长的大小
批量大小($B$): 是小批量计算中的批量大小batch size

2.2 基于异常检测的线性回归

  前一节讨论了这样一种情况：即一个特定的变量被认为是特殊的，最优平面是通过最小化该特殊变量的均方误差而确定的。而我们通常所说的异常检测中并不会对任何变量给与特殊对待，异常值的定义是基于基础数据点的整体分布，因此需要采用一种更一般的回归建模：即以相似的方式对待所有变量，通过最小化数据对该平面的投影误差确定最佳回归平面。在这种情况下，假设我们有一组变量 $X_1\dots X_d$， 对应的回归平面如下：

$$a_1\cdot X_1+\dots +a_d\cdot X_d+a_{d+1}=0$$

  为了后续计算的方便，对参数进行如下约束：
$$\sum _{i=1}^d{a}_i^2=1$$
  以$L_2$范数作为目标函数：
$$L={\Vert U\cdot A\Vert }_2$$

三、主成分分析法

前面介绍的最小二乘法只是试图找到一个（d-1）维超平面，它与数据具有最优拟合。主成分分析法可以解决这一问题的广义版本。具体来说，他可以找到任何维度的最佳表示超平面。

3.1基于样本的重构误差

3.1.1 思路

• 靠前的主成分主要解释了大部分正常的样本，而靠后的主成分主要解释了异常样本的方差
• 异常样本在靠前主成分上的投影较小，在靠后主成分上投影较大，只依靠靠在前面的主成分是无法完整的重构异常样本的
  • 只依靠排在前面的主成分被用于矩阵重构时，异常样本引起的重构误差是要远高于正常样本的
  • 重构误差越高的样本越有可能是异常样本
• 样本在靠后主成分上的偏差应赋予更高的权重
  • 令k为重构矩阵所用到的主成分的力量，则随着k的逐步增加，更多靠后的主成分被用于矩阵重构
  • 这些靠后的主成分对异常样本具有更高的线性表出能力，因此这些靠后的主成分上的偏差应被赋予更高的线性表出能力。

3.1.2 重构矩阵的生成方式

R为m*n型重构矩阵，
k为重构矩阵过程中用到的主成分的个数
Q为投影矩阵，其k个列向量为前k个主成分

3.1.3 重构误差与异常分数

异常得分
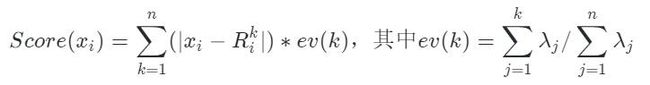k表示重构矩阵用到的主成分数，n表示主成分总数
ev(k)表示前k个主成分多大程度上解释了总体方差，与k值成正比

• 重构矩阵所用到的主成分越多(k值越大)，样本在靠后的主成分上的误差对应的权重ev(k)也越大
• 靠后主成分对异常样本具有更强的表达能力，从而对应的误差应赋予更高的权重

3.1.4基于KernelPCA重构误差的python实现

import numpy as np
from sklearn.decomposition import KernelPCA
from sklearn.preprocessing import StandardScaler

class KPCA_Recon_error:
    def __init__(self,matrix,contamination=0.01,kernel = 'rbf',gamma = None,random_state = 2018):
        self.matrix = StandardScaler.fit_transform(matrix)
        self.contamination = contamination
        self.kernel =kernel
        self.gamma = gamma
        self.random_state = random_state
    def ev_ration(self):
        transformer = KernelPCA(n_components=None,kernel=self.kernel,gamma=self.gamma,fit_inverse_transform=True,n_jobs=1)
        transformer.fit_transform(self.matrix)
        ev_ration =  np.cumsum(transformer.lambdas_)/np.sum(transformer.lambdas_)
        return ev_ration

    def recon_matrix(self):
        def reconstruct(recon_pc_num):
            transformer = KernelPCA(n_components=recon_pc_num,kernel=self.kernel,gamma=self.gamma,fit_inverse_transform=True,n_jobs=-1)
            X_transformed = transformer.fit_transform(self.matrix)
            #inverse_transform方法将降维后的矩阵重新映射到原来的特征空间
            recon_matrix = transformer.inverse_transform(X_transformed)
            assert recon_matrix.shape == self.matrix.shape,'重构矩阵的维度应与初始矩阵的维度一致'
            return recon_matrix
        col = self.matrix.shape[1]

        recon_matrics = list(map(reconstruct,range(1,col+1)))
        #检验生成的系列重构矩阵中是否存在重复
        i,j = np.random.choice(range(col),size = 2,replace = True)
        assert not np.allclose(recon_matrics[i],recon_matrics[j]),'不同数量主成分生成的重构矩阵是不相同的'
        return recon_matrics
    def anomaly_score(self):

        def vector_length(vector):
            square_sum = np.sum(np.square(vector))
            return np.sqrt(square_sum)
        #返回单个重构矩阵生成的异常分数
        def sub_score(recon_matrix,ev):
            delta = self.matrix-recon_matrix
            score = np.apply_along_axis(vector_length,axis=1,arr=delta)*ev
            return score
        ev_ration = self.ev_ration()
        anomaly_scores = map(sub_score,self.recon_matrix(),ev_ration)
        return sum(anomaly_scores)

    #根据特定的污染率返回异常分数最高的样本索引
    def anomaly_idx(self):
        idx_sort = np.argsort(-self.anomaly_score())
        anomaly_num = int(np.ceil(len(self.matrix)*self.contamination))
        anomaly_idx = idx_sort[:anomaly_num]
        return anomaly_idx
    #对样本集进行预测，若判定为异常样本，则返回1，否则返回0
    def predit(self):
        pred = [1 if i in self.anomaly_idx() else 0 for i in range(len(self.matrix))]
        return np.array(pred)

3.2 基于样本在major/minor主成分上的偏离程度

3.2.1 一些术语定义

• major principal components
  • 将特征值降序排列后，累计特征值之和约占50%的前几个特征值取极值对应的特征向量
  • 在major principal components上偏差较大的样本，对应于在原始特征上取极值的异常样本
    -minor principal components
  • 指特征值小于0.2对应的特征向量
  • 在 minor principal components偏差上较大的样本，对应于那些与正常样本相关性结构不一致的异常样本
• 样本在单个主成分上的偏差
  • 样本在此特征向量的偏离程度定义为样本在此特征向量上投影的平方与特征值之商
  • 其中除以特征值是为了起到归一化的作用，使得样本在不同特征向量上的偏差具有可比性
• 样本在所有方向上的偏差之和等价于它与样本中心之间的马氏距离

3.2.2算法流程

• 通过马氏距离筛选一定比例的极值样本从训练集中剔除，以获得鲁棒性更高的主成分及对应的特征值，令剩余样本构成的矩阵为remain_matrix
• 对remain_matrix进行主成分分析，得到主成分及对应的特征值
• 根据特征值的取值以及相关定义，确定major principal components和minor principal components
• 求remain_matrix 中所有样本在major principal components 和minor principal components上的偏离度
• 根据上一步求出的两个偏离度，以及指定的分位点，求出判定样本是否异常的阈值c1与c2
• 对于一个待检测样本，计算它在major principal components和minor principal components上的偏离度，若其中之一超出相应的阈值则判定为异常，否则为正常样本

3.3 实证分析

import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
from sklearn.ensemble import IsolationForest
from sklearn.preprocessing import StandardScaler


# variance_contrast函数返回一个列表indices_desc_topk，以及一个布尔值bool_result
# indices_desc_topk包含k个元素，指k个降幅最大的特征值对应的索引
# bool_result用于记录indices_desc_topk中是否包含最小或最大的索引
def variance_contrast(X, k=3, contamination=0.01):
    X = StandardScaler().fit_transform(X)
    pca = PCA(n_components=None, random_state=2018)  
    pca.fit(X)
    # variance_original为各主成分对应的特征值，即样本在主成分空间内的投影方差
    variance_original = pca.explained_variance_
    
    # 运用孤立森林进行异常检测，得到异常样本索引anomaly_indices
    iforest = IsolationForest(contamination=contamination, random_state=2018, n_jobs=-1, behaviour="new")  
    anomaly_pred = iforest.fit_predict(X)
    anomaly_indices = np.argwhere(anomaly_pred==-1).ravel()
    
    # 删除异常样本，得到矩阵X_trimmed
    X_trimmed = X[np.isin(range(len(X)), anomaly_indices, invert=True)]
    # 对X_trimmed进行PCA，求得特征值variance_revised
    pca.fit(X_trimmed)
    variance_revised = pca.explained_variance_
    
    # 对删除异常样本前后的特征值进行对比
    delta_ratio = (variance_revised - variance_original) / variance_original
    # 只选取delta_ratio中的负数，确保对应特征值是下降的
    target_ratio = delta_ratio[delta_ratio < 0]
    # k为预设参数，表示选取特征值减小幅度最大的前k个索引
    if len(target_ratio) >= k: 
        indices_desc_topk = np.argsort(target_ratio)[:k]
    else:
        indices_desc_topk = np.argsort(target_ratio)[:len(target_ratio)]
    
    # min_max_idx为最小与最大特征值对应的索引
    min_max_idx = [0,  X.shape[1]-1] 
    # 验证min_max_idx之中是否有任何一个索引出现在indices_desc_topk中
    bool_result = any(np.isin(min_max_idx, indices_desc_topk))
    return indices_desc_topk, bool_result

# generate_dataset用于生成实验数据集
def generate_dataset(seed, row=5000, col=20, contamination=0.01):
    rdg = np.random.RandomState(seed)
    outlier_num = int(row*contamination)
    inlier_num = row - outlier_num
    
    # 构造服从标准正态分布的正常样本集
    inliers = rdg.randn(inlier_num, col)
    
    # 如果col为奇数，col_1=col//2，否则col_1=int(col/2)
    col_1 = col//2 if np.mod(col, 2) else int(col/2)
    col_2 = col - col_1
    # outliers_sub_1服从标准伽玛分布；outliers_sub_2服从指数分布
    # outliers_sub_1、outliers_sub_2在axis=1方向上予以整合，构成异常样本集
    outliers_sub_1 = rdg.standard_gamma(1, (outlier_num, col_1))
    outliers_sub_2 = rdg.exponential(5, (outlier_num, col_2))
    outliers = np.c_[outliers_sub_1, outliers_sub_2]
    
    # 将inliers与outliers在axis=0方向上予以整合，构成实验数据集
    matrix = np.r_[inliers, outliers]
    return matrix

# 生成10个不重复的随机种子以及对应的数据集
seeds = np.random.RandomState(2018).choice(range(100), size=10, replace=False)
matrices = list(map(generate_dataset, seeds))

# 输出验证结果
contrast_result = list(map(variance_contrast, matrices))
verify_result = pd.DataFrame(contrast_result, columns=['特征值降幅最大索引', '包含最大最小索引'])
print(verify_result)

运行结果

四、线性模型的局限性

回归分析作为异常值检测的工具有一些局限性。

• 为了使回归分析技术有效，数据需要高度相关，并沿着低维子空间对齐。当数据不相关，但在某些区域高度聚类时，这些方法可能无法有效地工作。另一方面，即使数据在不同维度之间是成对的弱相关，由于属性间相关性的累积效应，通常情况下，低维度的子空间包含了数据中的大部分方差。

• 另一个相关问题是，数据中的相关性在本质上可能不是全局的。最近的一些分析性观察表明（具体见论文C. C. Aggarwal, and P. S. Yu. Finding Generalized Projected Clusters in High Dimensional Spaces, ACM SIGMOD Conference, 2000.），子空间相关性是特定于数据的特定位置的。在这种情况下，由PCA发现的全局子空间对于离群值分析是次优的。因此，为了创建更一般的局部子空间模型，有时将线性模型与近似模型结合起来是有用的。这将是高维和子空间离群点检测的主题。（有时间会在以后介绍）

• 与任何基于模型的方法一样，当使用一小组数据记录时，过拟合仍然是一个问题。在这种情况下，记录数量与数据维度之间的关系非常重要。例如，如果数据点的数量小于维度，就有可能找到一个或多个方差为零的方向。即使在数据大小比数据维数大(但相似)的情况下，也可以观察到相当大的偏差。

• 基于回归的方法的可解释性相当低。这些方法将数据投射到更低维的子空间中，这些子空间被表示为原始特征空间的线性(正或负)组合。在许多实际应用中，这很难用物理意义来解释。这还会减少用户对特定应用程序的内在知识。这是不可取的，因为通常能够解释为什么一个数据点在原始数据空间的特征方面是一个离群值是有趣的。

• 最后，当数据的维数较大时，该方法的计算复杂性可能是一个问题。当数据的维数为d时，会得到一个d × d的协方差矩阵，这个协方差矩阵可能相当大。此外，随着维数的增加，这个矩阵的对角化速度至少会降低二次。

参考文献

[1] 《Outlier Analysis》——Charu C. Aggarwal
[2] https://github.com/Albertsr
[3]https://github.com/datawhalechina/team-learning-data-mining/tree/master/AnomalyDetection