支持向量机伪代码_「机器学习」笔记2：支持向量机（SVM）原理、推导及Python代码实现...

本文首发于知乎专栏：

机器是怎样学习的​zhuanlan.zhihu.com

---

学习支持向量机时参考了很多大神的博客，和经典著作，从公式推导到代码实现，亲历亲为。

遇到很多疑惑，也是各种百度+Google，虽然最后也差不多都解决了，但终归是因为数学基础不扎实。

在这里做一个总结，以便以后复习。

有些地方加入了我自己的理解，仅作参考。

当然，如有疑问，请各位不吝赐教。

线性不可分的情况和核函数的部分本文没有涉及。（主要是作者本人也不是很懂。。。

参考文献及完整代码在文末。

码字不易，不如点赞支持一下这个推公式推到头秃的博主？

---

1. SVM解决的问题

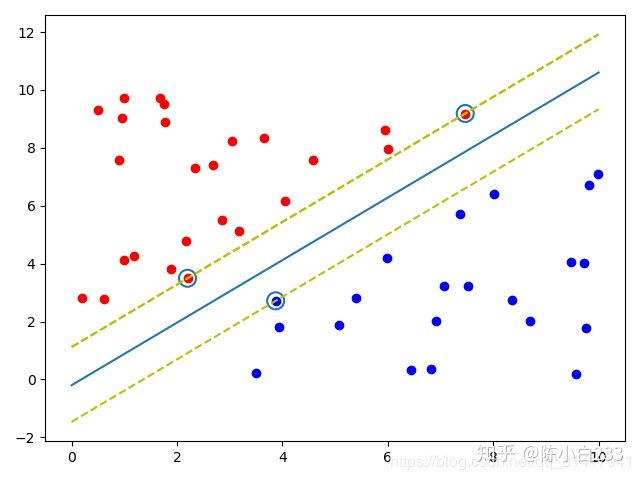
SVM解决的问题是经典的二元分类问题。给出一个分类标准使得样本集可以被最好地分类。在样本特征是二维的情况下，可以用下图表示

上图是我用Python实现的SVM分类器的最终结果图。

中间的实线是我们最终需要的分割线，在三维及以上的情况下叫做划分超平面。

画圈的样本是距离分割线最近的样本，叫做支持向量，这也是支持向量机名字的由来。两条黄色的虚线之间的距离叫做间隔，显然，这个间隔越大，也就代表两边的样本离分割线越远，我们得到的分割线就越鲁棒。

SVM的最终目的就是求出分割线的所有参数，在这个过程中还要确定样本中的支持向量是哪些。

2. 目标函数

我们的目的是找到使间隔最大的支持向量和分割平面，那么下面就要找到间隔的数学表达，也就是目标函数。

首先，样本集表示为：

其中，

,

.

是n维向量，为了便于可视化，我们以二维为例。 划分超平面表示为：

我们将这个超平面标记为

样本点到超平面的距离表示为：

假设超平面

可以将样本点正确分类，那么每个样本集中的点到超平面的距离

应该都大于等于支持向量（假设表示为

）到超平面的距离

:

那么支持向量与超平面的间隔就是不等式右边的部分。但是它过于复杂，所以这里对

进行缩放变换，使得

。这样处理对结果不会有影响，原因如下：

假设

，因为支持向量不在分割超平面上，所以

。因此只要两边同除

就可以了。

变换之后的不等式为：

两个异类支持向量之间的间隔表示为：

，就是目标函数。对上式两边同时乘以

可得，对样本集

的所有点满足：

合并一下就是：

《机器学习》书中对这部分的描述如下：

目标函数的数学表达：

为了方便计算，将上式取倒数，并对

取平方，得到最终需要优化的目标函数：

3. 目标函数的优化

如果没有约束条件，这就是一个简单的多项式求极值的问题，只需令一阶导数等于零，二阶导数小于零求出

的所有元素即可。 但是有了约束条件就要使用些特殊方法，比如

拉格朗日乘子法。

为什么要用拉格朗日乘子法？ 在特征维度低的线性问题中是可以不使用的，具体参考： https://www. zhihu.com/question/3669 4952

3.1 拉格朗日乘子法（Lagrange Multiplier）

这里简单介绍一下拉格朗日乘子法及KKT条件的原理和使用。 对有一个等式约束的凸函数优化问题：

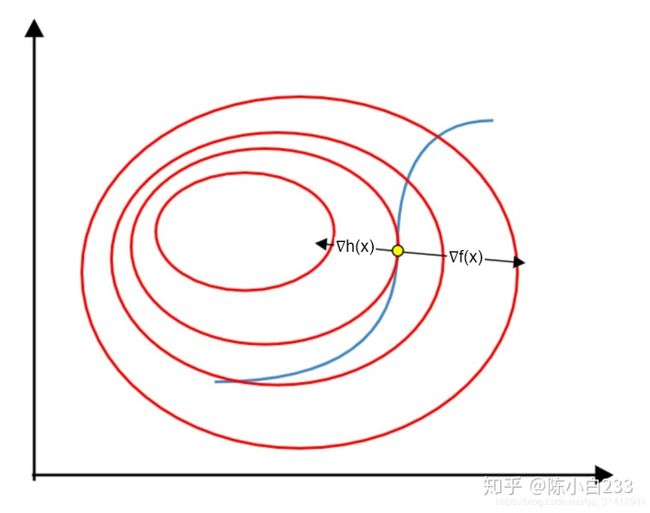
在三维的情况下，

是一个曲面，这个曲面在坐标轴 x-y 平面上的投影是一条曲线，也就是，看起来和 x-y 平面 “垂直”。

是一个凸函数，其与

相交。

上图中红色代表

的等值线，蓝色线代表

在x-y平面上的投影。

而两个曲面相交的部分是一条曲线，这条曲线在

曲面上的最低点（就是图中黄色的点）就是

取最小值的点。

这个点一定与

的某一条等值线相切。且在切点处两函数的梯度共线（可以同向或反向）。即存在

，使得在最小值点处：

其中，

是最小值点。此时，令拉格朗日函数为：

对该函数求导得：

显然，当

时，

。也就是说，

同时取得极小值。

也就是说，带有等式约束的优化问题转化为了不带约束条件的优化问题。

令

对

的导数都为0就可以得到最小值。

3.2 KKT条件

以上方法适用于在约束为等式的情况。当约束为不等式时，即:

极小值点的位置存在以下两种情况（以一个不等式约束为例）：

• 极小值点在
  区域内，此时可以忽略约束条件直接对
  求极小值即可，相当于把上节中的
  置零；
• 极小值点在边界
  上，此时与3.1节所述情况一样。
  唯一不同的是，在上图所示的极值点处，
  与
  的梯度方向一定相反。（如果它们梯度方向相同，就可以继续向两者减小的方向优化）

将以上两种情况结合可得，存在

使得：

由此引出

取得极小值的充分必要条件，即KKT(Karush-Kuhn-Tucker)条件：

原函数

转化为与上节形式相同的拉格朗日函数。

将这几种情况结合起来，推广到具有多个不等式或等式约束的优化问题上：

对有有限个约束的最小化问题：

其拉格朗日函数为：

KKT条件为：

3.3 对偶问题

现在我们回到第2节末尾，再看这个优化问题：

这就是个适用于不等式约束的优化。拉格朗日函数如下：

若要求

的最小值则首先把

看作常量，对

求关于

的最大值。因为

是小于等于0的，在

的前提下，其最大值就是：

。

因此，原问题可写为：

直接对该问题求解比较困难，因此这里引入对偶问题。

使用对偶问题求解的原因不止是为了计算方便，还是为线性不可分时核函数的引入作铺垫（本文不涉及这部分）。

先上结论：

也就是求取最大最小值的顺序发生了变化。从先对

求最大值变为先对

求最小值。

等式两边的问题互为对偶问题。

当然两个对偶问题同时取得最优解是有条件的，具体证明可以参考：

简易解说拉格朗日对偶（Lagrange duality）​www.cnblogs.com

转化为对偶问题后，令

的导数为0：

将上式代入

并化简可得：

化简过程如下：（公式太多还是手写吧emmm...）

化简后就只用求

即可。这样问题的复杂度就从与样本的维度有关变为只与样本数量有关了。

周志华的《机器学习》一书对这个最优解的几何意义有一段描述可以参考：

3.4 SMO(Sequential Minimal Optimazation)方法

上节最后得到的关于

的式子是一个二次规划问题，使用通用算法开销比较大。SMO方法是1998年提出的，用于求取SVM中的拉格朗日乘子，比通用算法更加高效。

其主要思想为，选取两个变量

，固定其他参数，对这两个参数进行优化，然后重复这个过程。

Note：选取$

$的标准：

不过博主有点懒，所以直接随机选取了。。。。需要深入了解可以参考《机器学习实战》（文末有下载方法~）

每次选取两个的原因是这些参数之间有约束

，只改变一个约束会被打破。

为了表示方便，记选取的两个参数为

，固定除

以外的参数：

带入

得：

为简便表示，下式中，

因为我们的最终目的是让

对

求导，而其他

已被固定，视为常数。且

也都是已知常数，所以将上式中不含

的常数项合并为

。

下一步，令其

的导数为0：

由上节可知：

注意到这个形式和上面的最后两项很相似，所以可以带进去计算。

但是需要注意的是这里的

是常量（否则带入一个变量并不利于求导结果的计算），所以这里的

中包含的

是初始化时赋予的值，将其记作

；把其他的

看作待更新的变量，记作

。

令

，得：

同时，因为需要求最大值，所以还要求对

的二阶导小于零：

到这里为止，

的更新已经完成，

可以通过两者之间的约束求得。

最后一步，就是求解参数

。

本文只采用了前一种方法，感兴趣的童鞋可以用（6.18）的方法试试，欢迎在评论区讨论~

具体操作如下：

假设更新过后的

，即该

对应的样本为支持向量，则满足

，结合更新之前的

：

解得：

4 软间隔

由于不是所有的数据集都可以完美的用一条线分割开，在两个类别中间可能会有个别样本点超过分割平面，使得数据集不能被完美分开。即便可以被分开，也有可能是过拟合造成的。

这时我们的算法需要对这些异常点进行容错，使其不影响数据集正常划分。

异常点的表示就是其不满足约束条件：

不过我们希望不满足约束的样本越少越好，因此将原问题改为：

是一个常数。当其取较大的值时，就迫使更多的样本趋于满足约束条件，取无穷大时就和原问题等价。

叫做“0/1损失函数”，数学表示为：

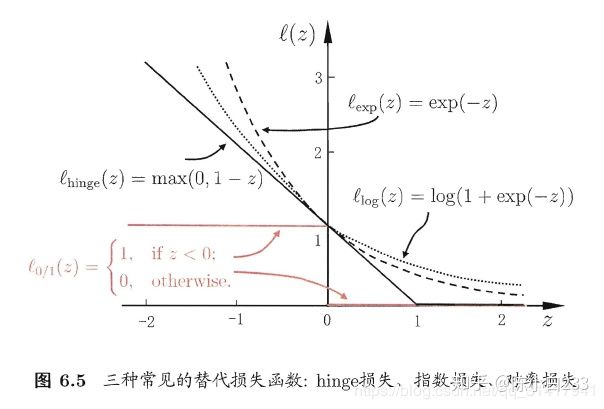
但是它数学性质不好，不连续，所以我们用合页损失函数（Hinge loss）代替：

如下图（图片来自《机器学习》）：

此时，优化目标变为：

这里有一个问题，按照合页损失函数的定义，把前面式子中的求和项带入，得到的结果应该是：

个人理解是，根据我们要解决的问题对hinge损失函数做了改动：

优化目标里含有max()，显然不便于计算，所以这里引入“松弛变量(slack variables)”

，表示每个样本不满足约束的程度。若样本

满足约束，则对应的

；若不满足，则

。优化目标可以重新写为：

和前面一样，重新使用拉格朗日乘子法。拉格朗日函数：

求解过程也和前面一样，贴个图：

和前面得到的结果对比一下，唯一不同的地方在于

的取值范围有了上界。这个上界来源于图片上的式（6.39），意义就是表示了算法对于样本点的容错程度。

5 代码

下面，我们将把以上的算法用Python程序实现。 首先我们对上面的算法步骤作一个总结，帮助我们理清思路：

整个SMO算法分为以下几个阶段：

• 选择
• 判断
• 计算
• 对
  做上下界限定，范围为
• 判断
  的改变量是否足够大，太小视为不变
• 计算
• 计算
• 重复以上步骤

5.1 数据集生成及一些辅助函数

写了一个简单的函数用来随机生成数据集。

指定一条曲线

，本例中是

，随机均匀生成100对数据，取值为[0, 10]，标为两个类别并画图表示。（为了突出两数据集的间隔，这里舍弃与分割线垂直距离小于1的点）

import 

随机选择第2个参数的下标：

def 

限制

的上下界：

def 

已知

求

：

def 

5.2 主函数

简化版的SMO算法：

def 

main函数：

dataset

*5.3 使用matplotlib绘图

如果想要可视化计算结果，可以在main函数后添加以下代码：

class1

6 github 地址

chenyr0021/machine_learning_exercises​github.com

7 参考文献

1. 《机器学习》，周志华
2. 《机器学习实战》，Peter Harrington
3. 简易解说拉格朗日对偶（Lagrange duality）
4. 支持向量机系列（5）——SMO算法解对偶问题
5. SVM为什么能够求解对偶问题，求解对偶问题为什么和原问题一样？为什么要求解对偶问题？svm的公式是什么？如果线性不可分怎么办？
6. 为什么支持向量机要用拉格朗日对偶算法来解最大化间隔问题？
7. 机器学习算法实践-SVM中的SMO算法
8. 支持向量机通俗导论（理解SVM的三层境界）

---

我必须吐槽一下知乎的编辑器了，，，

在知乎写技术文就像生活在石器时代

不支持markdown语法就算了，居然连我导入md文档都不支持公式自动转换

这么多公式一个一个重新编辑

不仅眼都要xia了

而且感觉头上更冷了：）

都看到这里了，不点赞支持一下头秃博主吗

---

知乎：@陈小白233
公众号：一本正经的搬砖日常

关注公众号即可获赠《机器学习》、《机器学习实战》电子书~