吴恩达机器学习笔记（四）多变量线性回归

本文章是笔者根据Coursera上吴恩达教授的机器学习课程来整理的学习笔记。如果是初学者，建议大家首先观看吴恩达教授的课程视频，然后再来看博文的要点总结。两者一起食用，效果更佳。

一、多维特征（Multiple Features）

之前讲过的房价预测问题是单一特征的，现在赋予其更多的特征，如下图：

多元线性回归模型：

二、多元梯度下降法

梯度下降法应用于多元线性回归模型：

求偏导数：左侧是单变量的公式，右侧是多变量的公式。

三、多元梯度下降法实操——特征缩放(Feature Scaling)

主要思想：让特征的取值范围相近，能够让梯度下降法更快地收敛。
下图中，左侧是未进行特征缩放的数据。x1取值范围远大于x2的取值范围，导致等高线呈非常细长的椭圆状，收敛很慢，甚至产生震荡。右侧是进行特征缩放后的，等高线比较均匀，能更快地收敛。

吴恩达教授建议的缩放范围是-3～3，-1/3～1/3。
各特征取值范围不要求完全相同，只要比较接近，就可使梯度下降算法正常工作。

均值归一化：
减均值，再除以标准差，或简单地直接除以最大值与最小值的差。

四、多元梯度下降法实操——学习率（Learning Rate）

debug的方法：
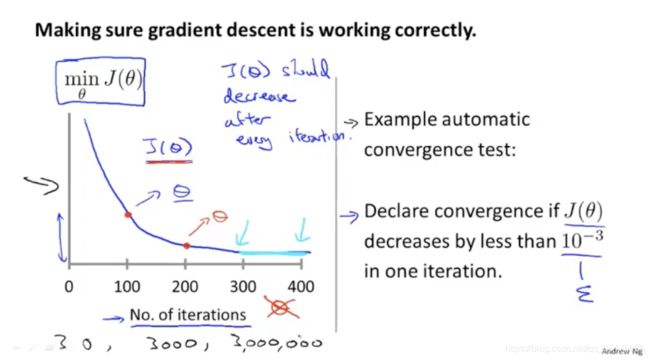
绘制出损失函数随着迭代次数的变化趋势。如果下降，说明梯度下降算法是正常工作的。
此外，还有自动测试是否收敛的方法。即设定一个很小的阈值，当损失函数下降速度小于阈值时，认为收敛。
吴恩达教授认为，很难确定一个合适的阈值，因此他更倾向于绘制图像来观察。
不同数据集下的梯度下降算法，收敛时的迭代次数很难提前预知，有的是300次即可收敛，有的是300万次才收敛。因此，有必要通过绘制图像来查看算法是否正常工作。

如果损失函数不是下降趋势的，而是上升，或先下降再上升再下降再上升等，很有可能是因为学习率过大。此时应该选用一个更小的学习率。

如果学习率太小，收敛太慢。
如果学习率太大，可能不是每次迭代都会下降，甚至发散。
吴恩达教授建议选去的学习率是，…0.001，0.003，0.01，0.03，0.1，0.3，1…取比能收敛的最大学习率稍小一些的数值作为学习率。

五、特征和多项式回归(Features and Polynomial Regression)

有些时候，不直接用现有的特征，而是根据现有特征构建出新的特征，能达到更好的效果。例如给出房子的长和宽两个特征，那么想到构建一个新的特征面积，是长和宽的乘积。只使用面积一个特征来进行预测。

有些时候，线性函数不能很好地拟合，我们想到多项式函数来拟合。如下图，用三次多项式来进行拟合。令x1=size, x2=size平方，x3=size立方，就转化成了之前讲过的多元线性模型。
注意：这里一定要进行特征缩放。

特征选择很重要：
因为二次函数会先上升再下降，所以不适合我们的图线。由此想到用三次函数来拟合。此外，我们还能想到，平方根也是一个很好的特征。平方根的整体呈上升趋势，但上升速度逐渐变缓，这与我们的图线趋势非常接近。

在后续的课程中，我们也将介绍一些能够自动选择特征的算法。

六、正规方程(Normal Equation)

对于某些线性问题，正规方程提供了一种很好的解析解法，一次性地来找到最优的参数。不需要像梯度下降法一样迭代很多次。

正规方程法的直观理解：
回忆求二次函数最小值的问题，找到导数为0的点，计算该点的函数值，就是最小值。
类似地，将实数延伸为向量，代价函数是关于向量的函数。那么找到使偏导数为0的点，该点的参数就是我们要求的最优值。但是这样求偏导数是非常复杂的，需要想一些简化的办法。

构建X矩阵：4个样本，5个特征（x0=1）。

构建X矩阵：m个样本，n个特征。下标表示特征编号，上标表示样本编号。（个人觉得，吴恩达教授的讲义图里面，m*2维矩阵中的上标和下标写反了）

根据数学知识可以证明，公式 $\theta =(X^{T}X{)}^{-1}{X}^{T}y$求得的 $\theta$ ，就是我们要求的使代价函数最小的 $\theta$。（此处不作详细证明）
使用正规方程法，不需要进行特征的缩放。如果三个特征的取值范围分别是0～1，0～1000，0～100000，也是没有问题的。

梯度下降法与正规方程法的优缺点对比：
梯度下降法：

• 缺点：需要选择合适的学习率。
• 缺点：需要很多次迭代。
• 优点：当特征值的数量n很大时，依然很有效。（n为几百万时表现也很好）

正规方程法：

• 优点：不需要选择合适的学习率。
• 优点：不需要迭代。
• 缺点：需要计算矩阵的逆 $\theta =(X^{T}X{)}^{-1}$，复杂度是$O(n^3)$
• 缺点：当特征值的数量n很大时，$\theta =(X^{T}X)$是 $n\ast n$维度的，高维矩阵求逆，速度非常慢。

怎么选择？
吴恩达教授建议，$n<10000$时，选择正规方程法。$n>10000$时，选择梯度下降法。

注意：梯度下降法除了适用于线性回归模型外，还适用于其他更复杂的模型（如后面即将讲到的Logistic回归）。而正规方程法仅仅适用于低维度的线性回归模型。对于很多其他复杂的算法，正规方程法并不适用。

七、正规方程在矩阵不可逆时的解决办法(Nomal Equation and Non-invertibility)

矩阵不可逆的情况极少发生。如果发生了，那么在octave中也能得到正解。因为octave的pinv函数可以计算伪逆。（正则化也可以解决矩阵不可逆的问题，在后续讲正则化的章节中会介绍）

矩阵不可逆的原因：
（1）有多余的特征（几个特征的相关性非常强）。如，将面积用不同单位表示，误认为是两个特征，这两个特征的相关性非常强，是线性相关，会导致矩阵不可逆。解决方案：删除多余的特征。
（2）特征数量太多($m<n$)。如，只有10条数据，但是有100个特征。解决方案：删除一些影响较小的特征，或使用正则化方法（后续课程中介绍）。