jq实现文字个数限制_非线性关系的分析方法限制性立方样条(Restricted cubic spline,RCS)...
作者:何强生,审稿:王九谊 在医学研究中,我们经常构建回归模型来分析自变量和因变量之间的关系。事实上,大多数的回归模型有一个重要的假设就是自变量和因变量呈线性关联,这个条件实际很难满足。常见的解决方法是将连续变量分类,但类别数目和节点位置的选择往往带有主观性,并且分类往往会损失信息。因此,一个更好的解决方法是拟合自变量与因变量之间的非线性关系,
限制性立方 (Restricted cubic spline,RCS)
就是分析非线性关系的最常见的方法之一 。 近年来在Lancet、BMJ等杂志经常见到利用限制性立方样条来拟合非线性关系。在之前医咖会R语言入门课程第18课《展示非线性关系》中也简单介绍过限制性立方样条的应用(R课程第18期:多项式回归、分段回归、限制性立方样条...)。 本文将以Lancet Diabetes Endocrinol杂志2018年的文章 《Association of BMI with overall and cause-specific mortality: a population-based cohort study of 3.6 million adults in the UK》 和作者模拟的数据为例,带领大家学习限制性立方样条的使用和结果解读。 在这篇文章中,作者使用限制性立方样条绘制BMI与死因之间的关系,第一个图形如下:
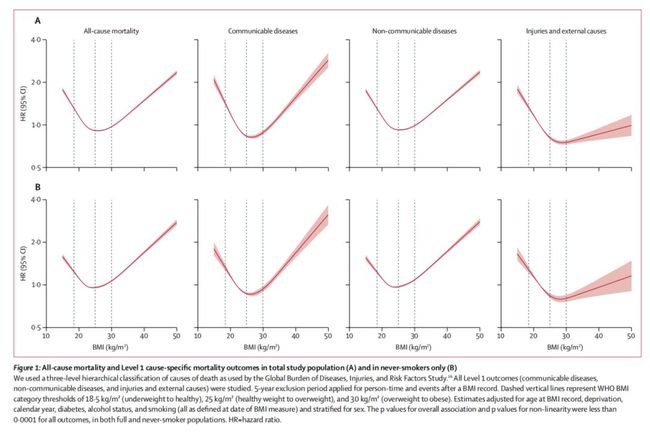 从图中我们可以看到,不管是在全人群还是非吸烟人群中,BMI与all-cause, communicable, and non-communicable disease mortality之间呈J型关系,死亡率最低点的BMI大概是25Kg/m
2。另外,对于injuries and external causes mortality而言,随着BMI的增加,死亡率在降低,但当BMI超过27Kg/m
2继续增加时,死亡率开始增加,但是增加幅度很小。 通过以上的例子,我们可以看到,使用限制性立方样条,可以很清晰的描述自变量与因变量之间的关系。事实上,限制性立方样条的应用范围非常广,凡是想描述自变量和因变量的关系都可以在回归模型中加入限制性立方样条,除了以上的例子中的COX回归外,还可以应用到线性回归、Logistic回归、以及Meta分析中剂量反应关系的Meta回归等。
从图中我们可以看到,不管是在全人群还是非吸烟人群中,BMI与all-cause, communicable, and non-communicable disease mortality之间呈J型关系,死亡率最低点的BMI大概是25Kg/m
2。另外,对于injuries and external causes mortality而言,随着BMI的增加,死亡率在降低,但当BMI超过27Kg/m
2继续增加时,死亡率开始增加,但是增加幅度很小。 通过以上的例子,我们可以看到,使用限制性立方样条,可以很清晰的描述自变量与因变量之间的关系。事实上,限制性立方样条的应用范围非常广,凡是想描述自变量和因变量的关系都可以在回归模型中加入限制性立方样条,除了以上的例子中的COX回归外,还可以应用到线性回归、Logistic回归、以及Meta分析中剂量反应关系的Meta回归等。
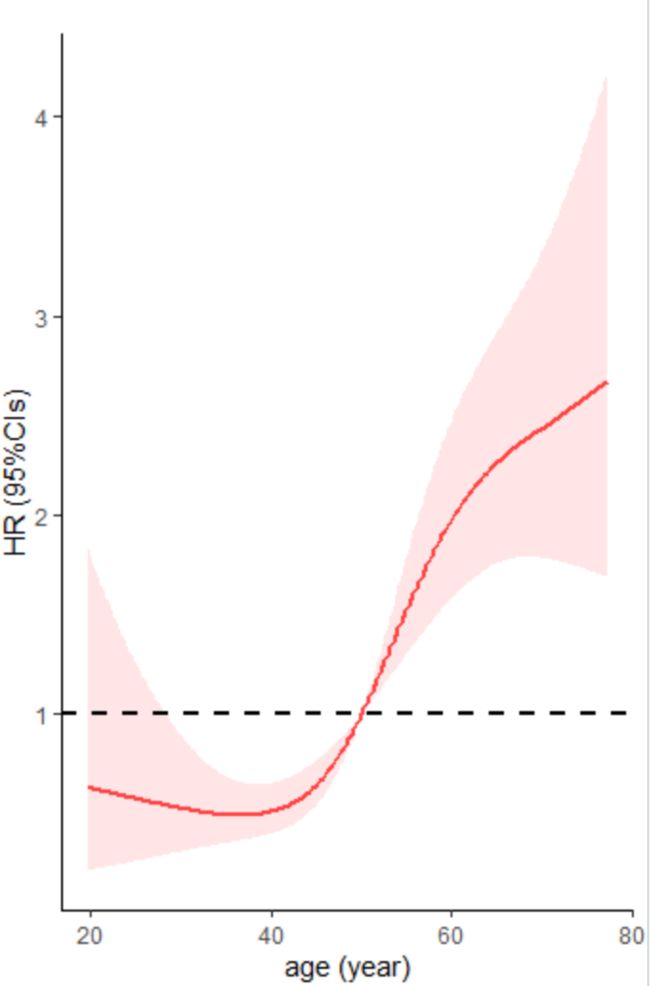
 ######自己画图 P2 geom_ribbon(data=HR, aes(age,ymin = lower, ymax = upper),alpha = 0.1,fill="red") ######进一步设置图形 P2 labs(title = "RCS", x="age", y="HR (95%CI)") P2
######自己画图 P2 geom_ribbon(data=HR, aes(age,ymin = lower, ymax = upper),alpha = 0.1,fill="red") ######进一步设置图形 P2 labs(title = "RCS", x="age", y="HR (95%CI)") P2
 ####如果想看是否存在非线性关系,可以使用anova() anova(fit)
####如果想看是否存在非线性关系,可以使用anova() anova(fit)
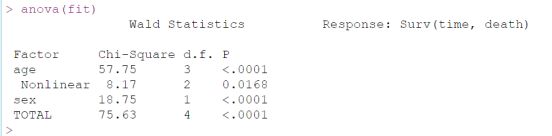 可以看到age整体是有意义的(包括线性或者非线性关联),然后看P-Nonlinear =0.0168<0.05,这里我们可以说年龄与死亡风险之间存在非线性关联。 如果自变量与关注的结局变量存在非线性关系,如何在文章中对结果更详细的描述呢,建议大家可以参照上文中提到的Lancet的文章。 个人还发现BMJ的一篇文章 《Predicted lean body mass, fat mass, and all cause and cause specific mortality in men: prospective US cohort study》 对于非线性关系描述的非常好,摘抄一部分放在这里供大家参考: In figure 1, we used restricted cubic splines to flexibly model and visualize the relation of predicted fat mass and lean body mass with all cause mortality in men. The risk of all cause mortality was relatively flat until around 21 kg of predicted fat mass and then started to increase rapidly afterwards (P for non-linearity <0.001). The average BMI for men with 21 kg of predicted fat mass was 25. Above 21 kg, the hazard ratio per standard deviation higher predicted fat mass was 1.22 (1.18 to 1.26). Regarding the strong U shaped relation between predicted lean body mass and all cause mortality, the plot showed a substantial reduction of the risk within the lower range of predicted lean body mass, which reached the lowest risk around 56 kg and then increased thereafter (P for non-linearity <0.001). Below 56 kg, the hazard ratio per standard deviation higher predicted lean body mass was 0.87 (0.82 to 0.92).
可以看到age整体是有意义的(包括线性或者非线性关联),然后看P-Nonlinear =0.0168<0.05,这里我们可以说年龄与死亡风险之间存在非线性关联。 如果自变量与关注的结局变量存在非线性关系,如何在文章中对结果更详细的描述呢,建议大家可以参照上文中提到的Lancet的文章。 个人还发现BMJ的一篇文章 《Predicted lean body mass, fat mass, and all cause and cause specific mortality in men: prospective US cohort study》 对于非线性关系描述的非常好,摘抄一部分放在这里供大家参考: In figure 1, we used restricted cubic splines to flexibly model and visualize the relation of predicted fat mass and lean body mass with all cause mortality in men. The risk of all cause mortality was relatively flat until around 21 kg of predicted fat mass and then started to increase rapidly afterwards (P for non-linearity <0.001). The average BMI for men with 21 kg of predicted fat mass was 25. Above 21 kg, the hazard ratio per standard deviation higher predicted fat mass was 1.22 (1.18 to 1.26). Regarding the strong U shaped relation between predicted lean body mass and all cause mortality, the plot showed a substantial reduction of the risk within the lower range of predicted lean body mass, which reached the lowest risk around 56 kg and then increased thereafter (P for non-linearity <0.001). Below 56 kg, the hazard ratio per standard deviation higher predicted lean body mass was 0.87 (0.82 to 0.92).
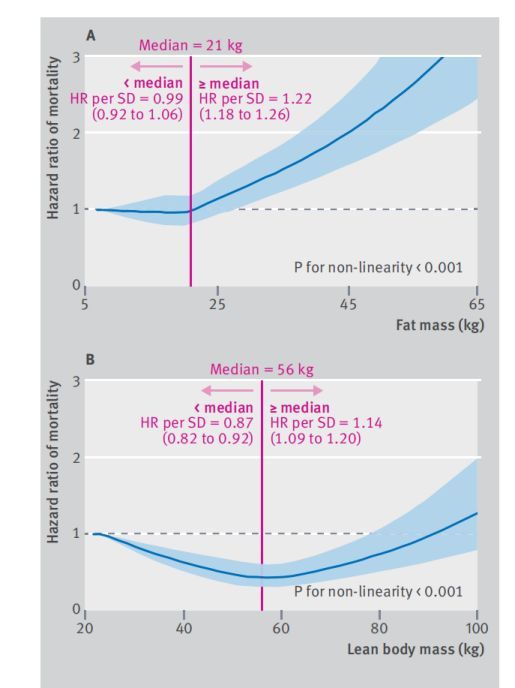 那么在方法部分如何描述使用了限制性立方样条,还是可以参照这篇文章: We also used restricted cubic splines with five knots at the 5th, 35th, 50th, 65th, and 95th centiles to flexibly model the association of lean body mass, fat mass, and BMI with mortality. 以上就是对限制性立方样条的简单介绍,原理和操作都比较简单。但加入到分析中,能更直观的描述感兴趣的自变量和因变量之间的关系,发现更有趣的点,可以为文章增色不少。对R不熟悉也不要紧,在sas和stata中也可以实现,感兴趣的同学可以去尝试。 [1] Bhaskaran K, Dos-Santos-Silva I, Leon DA, Douglas IJ, Smeeth L. Association of BMI with overall and cause-specific mortality: a population-based cohort study of 3·6 million adults in the UK. Lancet Diabetes Endocrinol. 2018;6(12):944–953. doi:10.1016/S2213-8587(18)30288-2. [2] Lee DH, Keum N, Hu FB, et al. Predicted lean body mass, fat mass, and all cause and cause specific mortality in men: prospective US cohort study. BMJ. 2018;362:k2575. Published 2018 Jul 3. doi:10.1136/bmj.k2575 [3] 罗剑锋, et al. "限制性立方样条在非线性回归中的应用研究%The Application of Restricted Cubic Spline in Nonlinear Regression." 中国卫生统计 027.003(2010):229-232.
那么在方法部分如何描述使用了限制性立方样条,还是可以参照这篇文章: We also used restricted cubic splines with five knots at the 5th, 35th, 50th, 65th, and 95th centiles to flexibly model the association of lean body mass, fat mass, and BMI with mortality. 以上就是对限制性立方样条的简单介绍,原理和操作都比较简单。但加入到分析中,能更直观的描述感兴趣的自变量和因变量之间的关系,发现更有趣的点,可以为文章增色不少。对R不熟悉也不要紧,在sas和stata中也可以实现,感兴趣的同学可以去尝试。 [1] Bhaskaran K, Dos-Santos-Silva I, Leon DA, Douglas IJ, Smeeth L. Association of BMI with overall and cause-specific mortality: a population-based cohort study of 3·6 million adults in the UK. Lancet Diabetes Endocrinol. 2018;6(12):944–953. doi:10.1016/S2213-8587(18)30288-2. [2] Lee DH, Keum N, Hu FB, et al. Predicted lean body mass, fat mass, and all cause and cause specific mortality in men: prospective US cohort study. BMJ. 2018;362:k2575. Published 2018 Jul 3. doi:10.1136/bmj.k2575 [3] 罗剑锋, et al. "限制性立方样条在非线性回归中的应用研究%The Application of Restricted Cubic Spline in Nonlinear Regression." 中国卫生统计 027.003(2010):229-232.
 从图中我们可以看到,不管是在全人群还是非吸烟人群中,BMI与all-cause, communicable, and non-communicable disease mortality之间呈J型关系,死亡率最低点的BMI大概是25Kg/m
2。另外,对于injuries and external causes mortality而言,随着BMI的增加,死亡率在降低,但当BMI超过27Kg/m
2继续增加时,死亡率开始增加,但是增加幅度很小。 通过以上的例子,我们可以看到,使用限制性立方样条,可以很清晰的描述自变量与因变量之间的关系。事实上,限制性立方样条的应用范围非常广,凡是想描述自变量和因变量的关系都可以在回归模型中加入限制性立方样条,除了以上的例子中的COX回归外,还可以应用到线性回归、Logistic回归、以及Meta分析中剂量反应关系的Meta回归等。
从图中我们可以看到,不管是在全人群还是非吸烟人群中,BMI与all-cause, communicable, and non-communicable disease mortality之间呈J型关系,死亡率最低点的BMI大概是25Kg/m
2。另外,对于injuries and external causes mortality而言,随着BMI的增加,死亡率在降低,但当BMI超过27Kg/m
2继续增加时,死亡率开始增加,但是增加幅度很小。 通过以上的例子,我们可以看到,使用限制性立方样条,可以很清晰的描述自变量与因变量之间的关系。事实上,限制性立方样条的应用范围非常广,凡是想描述自变量和因变量的关系都可以在回归模型中加入限制性立方样条,除了以上的例子中的COX回归外,还可以应用到线性回归、Logistic回归、以及Meta分析中剂量反应关系的Meta回归等。
什么是立方样条?
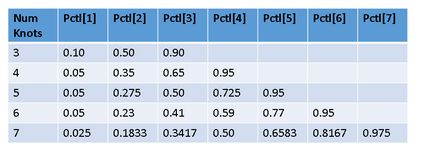
回归样条(regression spline)本质上是一个分段多项式, 但它一般要求每个分段点上连续并且二阶可导,这样可以保证曲线的平滑性。而限制性立方样条是在回归样条的基础上附加要求:样条函数在自变量数据范围两端的两个区间内为线性函数。 在利用限制性立方样条绘制曲线关系时,通常需要设置样条函数节点的个数(k)和位置(t i )。绝大多数情况下, 节点的位置对限制性立方样条的拟合影响不大, 而节点的个数则决定曲线的形状, 或者说平滑程度。当节点的个数为2时, 得到的拟合曲线就是一条直线, 大多数研究者推荐的节点为3-5个 。 在 《Regression Modeling Strategies》 这本书中,Harrell建议节点数为4时,模型的拟合较好,同时可以兼顾曲线的平滑程度和避免过拟合造成的精度降低。而当样本量较大时,例如因变量为未删失的连续变量并且大于100时,5个节点是更好的选择。小样本(如n<30)可以选择3个节点。以下是Harrell推荐的节点数和相应的节点位置,大家可以参考。案例说明(模拟数据)
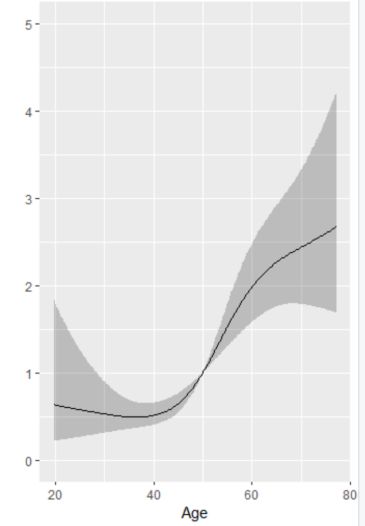
目前SAS、STATA、R等软件都可以进行限制性立方样条分析。基于画图的方便,我们以R语言为例进行说明。首先参照rms包,生成一个模拟数据集,包括性别(sex),年龄(age)以及生存时间(time)和结局变量(death)。 若想分析年龄和生存率之间关系,传统的方法可以在Cox回归中将年龄作为连续变量处理,也可以对年龄进行分组,这样的做法都无法更直观的呈现年龄与死亡风险之间的关联。以下我们 用限制性立方样条来分析年龄与死亡风险之间的关系 : #####加载所需要的包 library(ggplot2) library(rms) #####立方样条所需要的包 ###参照rms包,先生成一个模拟数据集,包括性别(sex),年龄(age)以及生存时间(time)和结局变量(death); n set.seed(731) age label(age) sex cens h time label(time) death time units(time) data #######开始正式画图 dd options(datadist='dd') #为后续程序设定数据环境 ####拟合cox回归模型,注意这里的R命令是“cph”,而不是常见的生存分析中用到的“coxph"命令 fit dd$limits$age[2] fit=update(fit) HR P1 P1 ######自己画图 P2 geom_ribbon(data=HR, aes(age,ymin = lower, ymax = upper),alpha = 0.1,fill="red") ######进一步设置图形 P2 labs(title = "RCS", x="age", y="HR (95%CI)") P2
######自己画图 P2 geom_ribbon(data=HR, aes(age,ymin = lower, ymax = upper),alpha = 0.1,fill="red") ######进一步设置图形 P2 labs(title = "RCS", x="age", y="HR (95%CI)") P2
 ####如果想看是否存在非线性关系,可以使用anova() anova(fit)
####如果想看是否存在非线性关系,可以使用anova() anova(fit)
 可以看到age整体是有意义的(包括线性或者非线性关联),然后看P-Nonlinear =0.0168<0.05,这里我们可以说年龄与死亡风险之间存在非线性关联。 如果自变量与关注的结局变量存在非线性关系,如何在文章中对结果更详细的描述呢,建议大家可以参照上文中提到的Lancet的文章。 个人还发现BMJ的一篇文章 《Predicted lean body mass, fat mass, and all cause and cause specific mortality in men: prospective US cohort study》 对于非线性关系描述的非常好,摘抄一部分放在这里供大家参考: In figure 1, we used restricted cubic splines to flexibly model and visualize the relation of predicted fat mass and lean body mass with all cause mortality in men. The risk of all cause mortality was relatively flat until around 21 kg of predicted fat mass and then started to increase rapidly afterwards (P for non-linearity <0.001). The average BMI for men with 21 kg of predicted fat mass was 25. Above 21 kg, the hazard ratio per standard deviation higher predicted fat mass was 1.22 (1.18 to 1.26). Regarding the strong U shaped relation between predicted lean body mass and all cause mortality, the plot showed a substantial reduction of the risk within the lower range of predicted lean body mass, which reached the lowest risk around 56 kg and then increased thereafter (P for non-linearity <0.001). Below 56 kg, the hazard ratio per standard deviation higher predicted lean body mass was 0.87 (0.82 to 0.92).
可以看到age整体是有意义的(包括线性或者非线性关联),然后看P-Nonlinear =0.0168<0.05,这里我们可以说年龄与死亡风险之间存在非线性关联。 如果自变量与关注的结局变量存在非线性关系,如何在文章中对结果更详细的描述呢,建议大家可以参照上文中提到的Lancet的文章。 个人还发现BMJ的一篇文章 《Predicted lean body mass, fat mass, and all cause and cause specific mortality in men: prospective US cohort study》 对于非线性关系描述的非常好,摘抄一部分放在这里供大家参考: In figure 1, we used restricted cubic splines to flexibly model and visualize the relation of predicted fat mass and lean body mass with all cause mortality in men. The risk of all cause mortality was relatively flat until around 21 kg of predicted fat mass and then started to increase rapidly afterwards (P for non-linearity <0.001). The average BMI for men with 21 kg of predicted fat mass was 25. Above 21 kg, the hazard ratio per standard deviation higher predicted fat mass was 1.22 (1.18 to 1.26). Regarding the strong U shaped relation between predicted lean body mass and all cause mortality, the plot showed a substantial reduction of the risk within the lower range of predicted lean body mass, which reached the lowest risk around 56 kg and then increased thereafter (P for non-linearity <0.001). Below 56 kg, the hazard ratio per standard deviation higher predicted lean body mass was 0.87 (0.82 to 0.92).
 那么在方法部分如何描述使用了限制性立方样条,还是可以参照这篇文章: We also used restricted cubic splines with five knots at the 5th, 35th, 50th, 65th, and 95th centiles to flexibly model the association of lean body mass, fat mass, and BMI with mortality. 以上就是对限制性立方样条的简单介绍,原理和操作都比较简单。但加入到分析中,能更直观的描述感兴趣的自变量和因变量之间的关系,发现更有趣的点,可以为文章增色不少。对R不熟悉也不要紧,在sas和stata中也可以实现,感兴趣的同学可以去尝试。 [1] Bhaskaran K, Dos-Santos-Silva I, Leon DA, Douglas IJ, Smeeth L. Association of BMI with overall and cause-specific mortality: a population-based cohort study of 3·6 million adults in the UK. Lancet Diabetes Endocrinol. 2018;6(12):944–953. doi:10.1016/S2213-8587(18)30288-2. [2] Lee DH, Keum N, Hu FB, et al. Predicted lean body mass, fat mass, and all cause and cause specific mortality in men: prospective US cohort study. BMJ. 2018;362:k2575. Published 2018 Jul 3. doi:10.1136/bmj.k2575 [3] 罗剑锋, et al. "限制性立方样条在非线性回归中的应用研究%The Application of Restricted Cubic Spline in Nonlinear Regression." 中国卫生统计 027.003(2010):229-232.
那么在方法部分如何描述使用了限制性立方样条,还是可以参照这篇文章: We also used restricted cubic splines with five knots at the 5th, 35th, 50th, 65th, and 95th centiles to flexibly model the association of lean body mass, fat mass, and BMI with mortality. 以上就是对限制性立方样条的简单介绍,原理和操作都比较简单。但加入到分析中,能更直观的描述感兴趣的自变量和因变量之间的关系,发现更有趣的点,可以为文章增色不少。对R不熟悉也不要紧,在sas和stata中也可以实现,感兴趣的同学可以去尝试。 [1] Bhaskaran K, Dos-Santos-Silva I, Leon DA, Douglas IJ, Smeeth L. Association of BMI with overall and cause-specific mortality: a population-based cohort study of 3·6 million adults in the UK. Lancet Diabetes Endocrinol. 2018;6(12):944–953. doi:10.1016/S2213-8587(18)30288-2. [2] Lee DH, Keum N, Hu FB, et al. Predicted lean body mass, fat mass, and all cause and cause specific mortality in men: prospective US cohort study. BMJ. 2018;362:k2575. Published 2018 Jul 3. doi:10.1136/bmj.k2575 [3] 罗剑锋, et al. "限制性立方样条在非线性回归中的应用研究%The Application of Restricted Cubic Spline in Nonlinear Regression." 中国卫生统计 027.003(2010):229-232.
更多阅读
1. R课程第18期:多项式回归、分段回归、限制性立方样条...
2. 建立非线性回归预测模型,来看R教程!
3. 如何理解线性回归的方差齐性检验
医咖会微信:medieco-ykh关注医咖会,及时获取最新统计教程!