【MXNet】（九）：NDArray实现一个简单的线性回归模型

本文一步一步实现一个简单的线性回归模型来了解一下深度学习是如何工作的，这里只用到NDArray和autograd来实现，并不使用其他任何框架。

首先导入包，

from IPython import display
from matplotlib import pyplot as plt
from mxnet import autograd, nd
import random

这里人工构造一个数据集。构造一个样本数为1000，特征个数为2的训练集，w=[2,−3.4]⊤，b=4.2，再加一个服从均值为0、标准差为0.01的正态分布的随机噪声项ϵ

下面生成数据集，

num_inputs = 2
num_examples = 1000
true_w = [2, -3.4]
true_b = 4.2
features = nd.random.normal(scale=1, shape=(num_examples, num_inputs))
labels = true_w[0] * features[:,0] + true_w[1] * features[:,1] + true_b
labels += nd.random.normal(scale=0.01, shape=labels.shape)

打印一个样本看一看是怎样的数据，

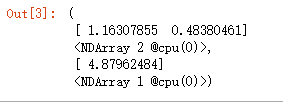
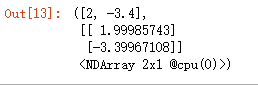
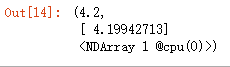
features[0],labels[0]

输出，

因为加了随机噪声，所以每次打印的输出可能不同。

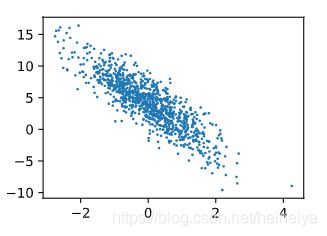
画出第二个特征features[:, 1]和标签 labels 的散点图，观察一下它们的线性关系。

def use_svg_display():
    display.set_matplotlib_formats('svg')

def set_figsize(figsize=(3.5, 2.5)):
    use_svg_display()
    plt.rcParams['figure.figsize'] = figsize
    
set_figsize()
plt.scatter(features[:,1].asnumpy(), labels.asnumpy(), 1)
plt.show()

输出，

在训练的时候，我们每次并不是会一次性处理全部的数据，而是每次读取小批量数据样本。

def data_iter(batch_size, features, labels):
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices)
    for i in range(0, num_examples, batch_size):
        j = nd.array(indices[i:min(i + batch_size, num_examples)])
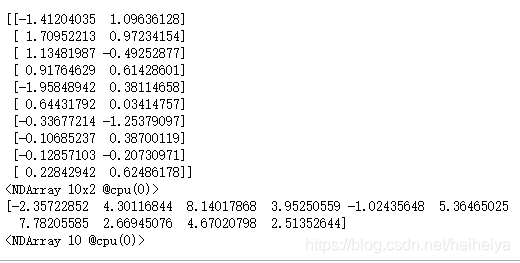
        yield features.take(j), labels.take(j)

假设每次读取10个样本数据，

batch_size = 10
for X, y in data_iter(batch_size, features, labels):
    print(X, y)
    break

输出，

现在将模型的权重初始化成均值为0、标准差为0.01的正态随机数，偏差则初始化成0。

w = nd.random.normal(scale=0.01, shape=(num_inputs, 1))
b = nd.zeros(shape=(1,))

创建权重的梯度，

w.attach_grad()
b.attach_grad()

现在来定义模型，

def linreg(X, w, b):
    return nd.dot(X, w) + b

以及模型的损失函数，

def squared_loss(y_hat, y):
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

采用小批量随机梯度下降算法来优化损失函数，

def sgd(params, lr, batch_size):
    for param in params:
        param[:] = param - lr * param.grad / batch_size

接下来就可以开始训练模型了。

lr = 0.03
num_epochs = 3
net = linreg
loss = squared_loss

for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        with autograd.record():
            l = loss(net(X, w, b), y)
        l.backward()
        sgd([w, b], lr, batch_size)
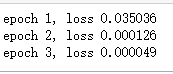
    train_l = loss(net(features, w, b), labels)
    print('epoch %d, loss %f' % (epoch + 1, train_l.mean().asnumpy()))

输出，

训练完成后，比较一下学习到的参数和真实值之间的差别，

true_w, w

输出，

true_b, b

输出，