深度学习4：网络优化Network Optimization（基于Python MXNet.Gluon框架）

应用中的两类难点问题

1. 优化问题：神经网络模型是一个非凸函数，再加上在深度网络中的梯度消失问题，很难进行优化；另外，深度神经网络模型一般参数比较多，训练数据也比较大，会导致训练的效率比较低；
2. 泛化问题：因为神经网络的拟合能力强，反而容易在训练集上产生过拟合。因此在训练深度神经网络时，同时也需要通过一定的正则化方法来改进网络的泛化能力。

网络优化

  深度神经网络是一个高度非线性的模型，其风险函数是一个非凸函数，因此风险最小化是一个非凸优化问题，会存在很多局部最优点。

  有效地学习深度神经网络的参数是一个具有挑战性的问题，其主要原因有以下几个方面：

• 网络结构多样性

  神经网络的种类非常多，比如卷积网络、循环网络等，其结构也非常不同。有些比较深，有些比较宽。不同参数在网络中的作用也有很大的差异，比如连接权重和偏置的不同，以及循环网络中循环连接上的权重和其它权重的不同。

  由于网络结构的多样性，我们很难找到一种通用的优化方法。不同的优化方法在不同网络结构上的差异也都比较大。

  此外，网络的超参数一般也比较多，这也给优化带来很大的挑战。

• 高维变量的非凸优化

  低维空间的非凸优化问题主要是存在一些局部最优点。基于梯度下降的优化方法会陷入局部最优点，因此低维空间非凸优化的主要难点是如何选择初始化参数和逃离局部最优点。

  在高维空间中，非凸优化的难点并不在于如何逃离局部最优点，而是如何逃离鞍点（SaddlePoint）。鞍点的梯度是0，但是在一些维度上是最高点，在另一些维度上是最低点，如图所示。

  在高维空间中，局部最优点要求在每一维度上都是最低点，这种概率非常低。假设网络有 10,000 维参数，一个点在某一维上是局部最低点的概率为 $p$，那么在整个参数空间中，局部最优点的概率为 $p^{10,000}$ ，这种可能性非常小。也就是说高维空间中，大部分梯度为 0 的点都是鞍点。基于梯度下降的优化方法会在鞍点附近接近于停滞，同样很难从这些鞍点中逃离。

  深度神经网络的参数非常多，并且有一定的冗余性，这使得每单个参数对最终损失的影响都比较小，这导致了损失函数在局部最优点附近是一个平坦的区域，称为平坦最小值（Flat Minima）。并且在非常大的神经网络中，大部分的局部最小值是相等的。虽然神经网络有一 定概率收敛于比较差的局部最小值，但随着网络规模增加，网络陷入局部最小值的概率大大降低。下图给出了一种简单的平坦底部示例。

优化算法

  目前，深度神经网络的参数学习主要是通过梯度下降法来寻找一组可以最小化结构风险的参数。在具体实现中，梯度下降法可以分为：批量梯度下降、随机梯度下降以及小批量梯度下降三种形式。根据不同的数据量和参数量，可以选择一 种具体的实现形式。除了在收敛效果和效率上的差异，这三种方法都存在一些共同的问题，比如：

1. 如何改进优化算法；
2. 如何初始化参数；
3. 如何预处理数据等。

小批量梯度下降

  在训练深度神经网络时，训练数据的规模通常都比较大。如果在梯度下降时，每次迭代都要计算整个训练数据上的梯度，这就需要比较多的计算资源。另外大 规模训练集中的数据通常会非常冗余，也没有必要在整个训练集上计算梯度。因此，在训练深度神经网络时，经常使用小批量梯度下降法（Mini-Batch Gradient Descent）。

  令 $f(\text{x};\theta )$ 表示一个深度神经网络，$\theta$ 为网络参数，在使用小批量梯度下降进行优化时，每次选取 $K$ 个训练样本 ${\mathcal{S}}_t=\{({\text{x}}^{(k)},{\text{y}}^{(k)}){\}}_{k=1}^K$。第 $t$ 次迭代（Iteration）时损失函数关于参数 $\theta$ 的偏导数为

$${\mathcal{G}}_t(\theta )=\frac{1}{K}\sum _{(\text{x},\text{y})\in {\mathcal{S}}_t}\frac{\partial \mathcal{L}(\text{y},f(\text{x};\theta ))}{\partial \theta }$$

其中 $\mathcal{L}(\cdot )$ 可微分的损失函数，$K$ 称为批量大小（Batch Size）。

  第 $t$ 次更新的梯度 $g_t$ 定义为

$$g_t={\mathcal{G}}_t({\theta }_{t-1})$$

  使用梯度下降来更新参数，

$${\theta }_t\leftarrow {\theta }_{t-1}-\alpha g_t$$

其中 $\alpha >0$ 为学习率。

  每次迭代时参数更新的差值 $\Delta {\theta }_t$ 定义为

$$\Delta {\theta }_t={\theta }_t-{\theta }_{t-1}$$

$\Delta {\theta }_t$ 和 $g_t$ 不需要完全一致。$\Delta {\theta }_t$ 为每次迭代时参数的实际更新方向，即 ${\theta }_t={\theta }_{t-1}+\Delta {\theta }_t$。

  在标准的小批量梯度下降中，$\Delta {\theta }_t=-\alpha g_t$.

  从上面公式可以看出，影响小批量梯度下降法的主要因素有：（1）批量大小 $K$、（2）学习率 $\alpha$ 以及（3）梯度估计。

  为了更有效地训练深度神经网络，在标准的小批量梯度下降法的基础上，也经常使用一些改进方法以加快优化速度，比如如何选择批量大小、如何调整学习率以及如何修正梯度估计。我们分别从这三个方面来介绍在神经网络优化中常用的算法。这些改进的优化算法也同样可以应用在批量或随机梯度下降法上。

批量大小 $K$ 的选择

  在小批量梯度下降法中，批量大小（Batch Size）对网络优化的影响也非常大。

  一般而言，批量大小不影响随机梯度的期望，但是会影响随机梯度的方差。

批量大小和学习率设置的关系
批量大小越大	批量大小越小
随机梯度的方差越小，引入的噪声也越小，训练也越稳定
因此可以设置较大的学习率	需要设置较小的学习率，否则模型会不收敛

  学习率 $\alpha$ 通常要随着批量大小的 $K$ 增大而相应地增大。一个简单有效的方法是线性缩放规则（Linear Scaling Rule）：当批量大小增加 $m$ 倍时， 学习率也增加 $m$ 倍。线性缩放规则往往在批量大小比较小时适用，当批量大小非常大时，线性缩放会使得训练不稳定。

  下图给出了从 Epoch（回合）和 Iteration（单次更新）的角度，批量大小对损失下降的影响。每一次小批量更新为一次 Iteration，所有训练集的样本更新一遍为一次 Epoch，两者的关系为 1 个 Epoch 等于$\frac{训练样本的数量N}{批量大小K}$ 次 Iterations。

  从第一张图可以看出，批量大小越大，下降效果越明显，并且下降曲线越平滑。但从第二张图可以看出，如果按整个数据集上的回合（Epoch）数来看，则是批量样本数越小，适当小的批量大小会导致更快的收敛。

学习率 $\alpha$ 的调整

  学习率是神经网络优化时的重要超参数。在梯度下降法中，学习率 $\alpha$ 的取值非常关键，如果过大就不会收敛，如果过小则收敛速度太慢。

  常用的学习率调整方法包括学习率衰减、学习率预热、周期性学习率调整以及一些自适应调整学习率的方法，比如 AdaGrad、RMSprop、AdaDelta 等。自适应学习率方法可以针对每个参数设置不同的学习率。

学习率衰减

  从经验上看，学习率在一开始要保持大些来保证收敛速度，在收敛到最优点附近时要小些以避免来回振荡。比较简单的学习率调整可以通过学习率衰减（Learning Rate Decay）的方式来实现，也称为学习率退火（Learning Rate Annealing）。

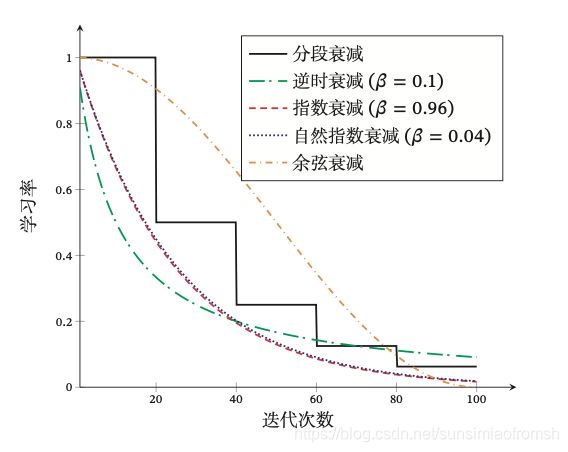
  不失一般性，这里的衰减方式设置为按迭代次数进行衰减。假设初始化学习率为 ${\alpha }_0$，在第 $t$ 次迭代时的学习率 ${\alpha }_t$。常见的衰减方法有以下几种：

  分段常数衰减（Piecewise Constant Decay）：即每经过 $T_1,T_2,\cdots ,T_m$ 次迭代将学习率衰减为原来的 ${\beta }_1,{\beta }_2,\cdots ,{\beta }_m$ 倍，其中 $T_m$ 和 ${\beta }_m<1$ 为根据经验设置的超参数。分段常数衰减也称为阶梯衰减（Step Decay）。

  逆时衰减（Inverse Time Decay）：

$${\alpha }_t={\alpha }_0\frac{1}{1+\beta t}$$

其中 $\beta$ 为衰减率。

  指数衰减（Exponential Decay）：

$${\alpha }_t={\alpha }_0{\beta }^t$$

其中 $\beta <1$ 为衰减率。

  自然指数衰减（Natural Exponential Decay）：

$${\alpha }_t={\alpha }_{0}exp(-\beta t)$$

其中 $\beta$ 为衰减率。

  余弦衰减（Cosine Decay）：

$${\alpha }_t=\frac{1}{2}{\alpha }_0(1+cos(\frac{t\pi }{T}))$$

其中 $T$ 为总的迭代次数。

下图给出了不同衰减方法的示例（假设初始学习率为 1）。

学习率预热

  在小批量梯度下降法中，当批量大小的设置比较大时，通常需要比较大的学习率。但在刚开始训练时，由于参数是随机初始化的，梯度往往也比较大，再加上比较大的初始学习率，会使得训练不稳定。

  为了提高训练稳定性， 我们可以在最初几轮迭代时，采用比较小的学习率，等梯度下降到一定程度后再恢复到初始的学习率，这种方法称为学习率预热（Learning Rate Warmup）。

  一个常用的学习率预热方法是逐渐预热（Gradual Warmup）。假设预热的迭代次数为 $T^{\prime }$，初始学习率为 ${\alpha }_0$，在预热过程中，每次更新的学习率为

$${\alpha }_t^{\prime }=\frac{t}{T^{\prime }}{\alpha }_0,1\le t\le T^{\prime }$$

当预热过程结束，再选择一种学习率衰减方法来逐渐降低学习率。

周期性学习率调整

  为了使得梯度下降法能够逃离局部最小值或鞍点，一种经验性的方式是在训练过程中周期性地增大学习率。虽然增大学习率可能短期内有损网络的收敛稳定性，但从长期来看有助于找到更好的局部最优解。

  一般而言，当一个模型收敛一个平坦（Flat）的局部最小值时，其鲁棒性会更好，即微小的参数变动不会剧烈影响模型能力；而当模型收敛到一个尖锐（Sharp）的局部最小值时，其鲁棒性也会比较差。

  具备良好泛化能力的模型通常应该是鲁棒的，因此理想的局部最小值应该是平坦的。周期性学习率调整可以使得梯度下降法在优化过程中跳出尖锐的局部极小值，虽然会短期内会损害优化过程，但最终会收敛到更加理想的局部极小值。

  下面介绍两种常用的周期性调整学习率的方法：循环学习率和带热重启的随机梯度下降。

循环学习率 一种简单的方法是使用循环学习率（Cyclic Learning Rate），即让学习率在一个区间内周期性地增大和缩小。通常可以使用线性缩放来调整学习率，称为三角循环学习率（Triangular Cyclic Learning Rate）。假设每个循环周期的长度相等都为 2Δ，其中前 Δ 步为学习率线性增大阶段， 后 Δ 步为学习率线性缩小阶段。在第 $t$ 次迭代时，其所在的循环周期数 $m$ 为

$$m=[1+\frac{t}{2\Delta T}]$$

其中 ⌊⋅⌋ 表示“向下取整”函数。第 $t$ 次迭代的学习率为

带热重启的随机梯度下降 带热重启的随机梯度下降（Stochastic Gradient De- scent with Warm Restarts，SGDR）是用热重启方式来替代学习率衰减的方法。学习率每间隔一定周期后重新初始化为某个预先设定值，然后逐渐衰减。每次重启后模型参数不是从头开始优化，而是从重启前的参数基础上继续优化。

  假设在梯度下降过程中重启 $M$ 次，第 $m$ 次重启在上次重启开始第 $T_m$ 个回合后进行，$T_m$ 称为重启周期。在第 $m$ 次重启之前，采用余弦衰减来降低学习率。第 $t$ 次迭代的学习率为

  下图给出了两种周期性学习率调整的示例（假设初始学习率为 1），每个周期中学习率的上界也逐步衰减。

AdaGrad 算法

  在标准的梯度下降法中，每个参数在每次迭代时都使用相同的学习率。由于每个参数的维度上收敛速度都不相同，因此根据不同参数的收敛情况分别设置学习率。

  AdaGrad（Adaptive Gradient）算法是借鉴 $l_2$ 正则化的思想，每次迭代时自适应地调整每个参数的学习率。在第 $t$ 次迭代时，先计算每个参数梯度平方的累计值

  在 AdaGrad 算法中，如果某个参数的偏导数累积比较大，其学习率相对较小；相反，如果其偏导数累积较小，其学习率相对较大。但整体是随着迭代次数的增加，学习率逐渐缩小。

  AdaGrad 算法的缺点是在经过一定次数的迭代依然没有找到最优点时，由于这时的学习率已经非常小，很难再继续找到最优点。

RMSprop 算法

  RMSprop算法是 Geoff Hinton 提出的一种自适应学习率的方法，可以在有些情况下避免 AdaGrad 算法中学习率不断单调下降以至于过早衰减的缺点。

  RMSprop 算法首先计算每次迭代梯度 ${\text{g}}_t$ 平方的指数衰减移动平均，

  从上式可以看出，RMSProp 算法和 AdaGrad 算法的区别在于 $G_t$ 的计算由累积方式变成了指数衰减移动平均。在迭代过程中，每个参数的学习率并不是呈衰减趋势，既可以变小也可以变大。

AdaDelta 算法

  AdaDelta(算)法也是 AdaGrad 算法的一个改进。和 RM- Sprop 算法类似，AdaDelta 算法通过梯度平方的指数衰减移动平均来调整学习率。此外，AdaDelta 算法还引入了每次参数更新差值 Δ 的平方的指数衰减权移 动平均。

  第 $t$ 次迭代时，参数更新差值 Δ 的平方的指数衰减权移动平均为

  从上式可以看出，AdaDelta 算法将 RMSprop 算法中的初始学习率 $\alpha$ 改为动态计算的 $\sqrt{\Delta X_{t-1}^2}$，在一定程度上平抑了学习率的波动。

梯度估计修正

  除了调整学习率之外，还可以进行梯度估计（Gradient Estimation）的修正。随机梯度下降方法中每次迭代的梯度估计和整个训练集上的最优梯度并不一致，具有一定的随机性。一种有效地缓解梯度估计随机性的方式是通过使用最近一段时间内的平均梯度来代替当前时刻的随机梯度来作为参数更新的方向，从而提高优化速度。

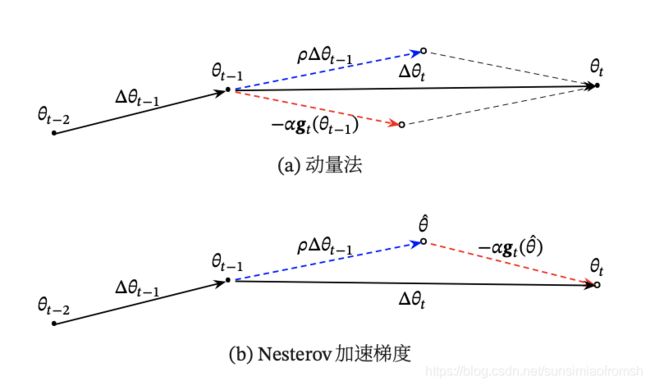
动量法

Nesterov 加速梯度

Adam 算法

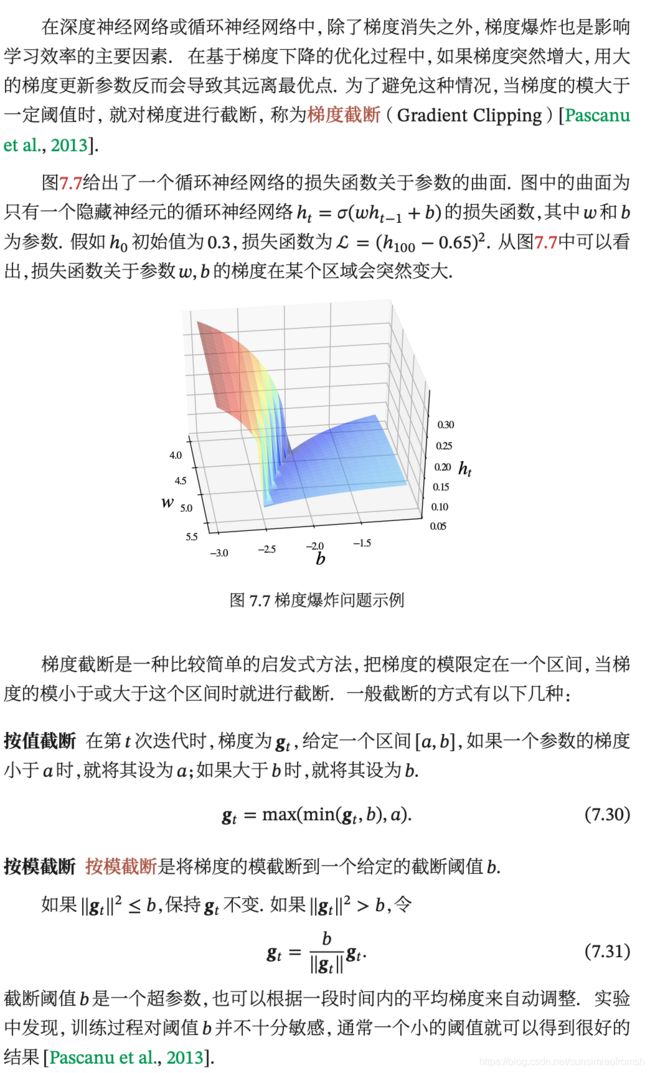
梯度截断

优化算法小结

参数初始化

  神经网络训练过程中的参数学习是基于梯度下降法进行优化的。梯度下降法需要在开始训练时给每一个参数赋一个初始值。这个初始值的选取十分关键。在感知器和logistic回归的训练中，我们一般将参数全部初始化为0。但是这在神经网络的训练中会存在一些问题。因为如果参数都为 0，在第一遍前向计算时，所有的隐层神经元的激活值都相同。这样会导致深层神经元没有区分性。这种现象也称为对称权重现象。

  为了打破这个平衡，比较好的方式是对每个参数都随机初始化，这样使得不同神经元之间的区分性更好。

  随机初始化参数的一个问题是如何选取随机初始化的区间。如果参数取的太小，一是会导致神经元的输入过小，经过多层之后信号就慢慢消失了；二是还会使得 Sigmoid 型激活函数丢失非线性的能力。

  以 Logistic 函数为例，在 0 附近基本上是近似线性的。这样多层神经网络的优势也就不存在了。如果参数取的太大，会导致输入状态过大。对于 Sigmoid 型激活函数来说，激活值变得饱和，从而导致梯度接近于 0。

  经常使用的初始化方法有以下两种：

高斯分布初始化 参数从一个固定均值（比如0）和固定方差（比如0.01）的高斯分布进行随机初始化；

均匀分布初始化 在一个给定的区间[−,] 内采用均匀分布来初始化参数。超参数 的设置可以按神经元的连接数量进行自适应的调整。

  初始化一个深层网络时，一个比较好的初始化策略是保持每个神经元输入和输出的方差一致。介绍两种参数初始化的方法。

Xavier 初始化

  Xavier初始化根据每层的神经元数量来自动计算初始化参数的方差，控制每个神经元的输入和输出的方差一致，在计算出参数的理想方差后，通过高斯分布或均匀分布来随机初始化参数。

  假设第 $l$ 层的一个隐藏层神经元 $z^{(l)}$ 其接收前一层的 $M_{l-1}$ 个神经元的输出 $a_i^{(l-1)},1\le i\le M_{l-1}$，

$$z^{(l)}=\sum _{i=1}^{M_{l-1}}{w}_i^{(l)}{a}_i^{(l-1)}$$

其中 $w_i^{(l)}$ 为参数。为了避免初始化参数使得激活值变得饱和，我们需要尽量使得 $z^{(l)}$ 处于激活函数的线性区间，也就是其绝对值比较小的值. 这时该神经元的激活值为 $a^{(l)}=f(z^{(l)})\approx z^{(l)}$.

  假设 $w_i^{(l)}$ 与 $a_i^{(l-1)}$ 的均值都为0，且相互独立，则 $a^{(l)}$ 的均值为0，$a^{(l)}$ 的方差为

$$var[a^{(l)}]=M_{l-1}var[w_i^{(l-1)}]var[a_i^{(l-1)}]$$

也就是说，输入信号的方差在经过该神经元后被放大或缩小了 $M_{l-1}var[w_i^{(l-1)}]$ 倍。为了使得在经过多层网络后，信号不被过分放大或过分减弱，我们尽可能保持每个神经元的输入和输出的方差一致。这样 $M_{l-1}var[w_i^{(l-1)}]$ 设为1比较合理。即

$$var[w_i^{(l-1)}]=\frac{1}{M_{l-1}}$$

  同理，为了使得在反向传播中，误差信号也不被放大或缩小，需要将 $w_i^{(l)}$ 的方差保持为

$$var[w_i^{(l-1)}]=\frac{1}{M_l}$$

  作为折中，同时考虑信号在前向和反向传播中都不被放大或缩小，可以设置

$$var[w_i^{(l-1)}]=\frac{2}{M_l+M_{l-1}}$$

  在计算出参数的理想方差后，可以通过高斯分布或均匀分布来随机初始化参数。

高斯分布初始化 当采用高斯分布来随机初始化参数时，连接权重 $w_i^{(l)}$ 可以按 $N(0,\sqrt{\frac{2}{M_l+M_{l-1}}})$；

均匀分布初始化 假设随机变量 $x$ 在区间 $[a,b]$ 内均匀分布，则其方差为 $var(x)=\frac{(b-a{)}^2}{12}$。因此，若采用区间为 $[-r,r]$ 的均分分布来初始化 $w_i^{(l)}$ 并满足 $var[w_i^{(l-1)}]=\frac{2}{M_l+M_{l-1}}$，则即均匀分布 $[-\sqrt{\frac{6}{M_l+M_{l-1}}},\sqrt{\frac{6}{M_l+M_{l-1}}}]$。

He 初始化

  当第 $l$ 层神经元使用 ReLU 激活函数时，通常有一半的神经元输出为 0，因此其分布的方差也近似为使用 Logistic 作为激活函数时的一半。这样，只考虑前向传播时，参数 $w_i^{(l)}$ 的理想方差为

$$var[w_i^{(l)}]=\frac{2}{M_{l-1}}$$

其中 $M_{l-1}$ 是第 $l-1$ 层神经元个数。

  因此使用 ReLU 激活函数时，若采用高斯分布来初始化参数 $w_i^{(l)}$，其方差为 $\frac{2}{M_{l-1}}$；若采用区间为 $[-r,r]$ 的均匀分布来初始化参数 $w_i^{(l)}$，则 $r=\sqrt{\frac{6}{M_{l-1}}}$。这种方法称为 He 初始化。

数据预处理

缩放归一化

  缩放归一化是一种非常简单的归一化方法，通过缩放将每一个特征的取值范围归一到 [0,1] 或 [−1,1] 之间。

标准归一化

  标准归一化也叫 z-score 归一化，来源于统计上的标准分数。将每一个维特征都调整为均值为 0，方差为 1。

白化

  白化（Whitening）是一种重要的预处理方法，用来降低输入数据特征之间的冗余性。输入数据经过白化处理后，特征之间相关性较低，并且所有特征具有相同的方差。白化的一个主要实现方式是使用主成分分析（Principal Component Analy- sis，PCA）方法去除掉各个成分之间的相关性。

逐层归一化

批量归一化

层归一化

权重归一化

局部响应归一化

部分优化方法代码

批量归一化

  仅在get_net中所有卷积层和全连接层之后、激活层之前加入批量归一化，看看运算结果有何变化——批量归一化处理后，发现有一些过拟合问题，可尝试权重衰减和丢弃法改进。在这里，仅仅用批量归一化而导致过拟合的代码就不再赘述，我们直接从两个办法来解决出现的过拟合问题。

丢弃法

import mxnet
from mxnet import gluon, init, nd, autograd
from mxnet.gluon import data as gdata
import d2lzh as d2l
from mxnet.gluon import loss as gloss, nn
import time
import random
import numpy as np
%matplotlib inline
from IPython import display
from matplotlib import pyplot as plt
import sys

mnist_train = gdata.vision.FashionMNIST(train=True)
#mnist_test = gdata.vision.FashionMNIST(train=False)

  在LeNet网络的所有卷积层和全连接层之后、激活层之前加入批量归一化，并使用丢弃法。

  对每个激活函数的输出使用丢弃法。我们可以分别设置各个层的丢弃概率。通常的建议是把靠近输入层的丢弃概率设得小一点。

drop_prob1, drop_prob2, drop_prob3, drop_prob4 = 0.1, 0.1, 0.1, 0.2 # 丢弃概率
def get_net():
    net = nn.Sequential()
    net.add(nn.Conv2D(6, kernel_size=5),
            nn.BatchNorm(), # 批量归一化
            nn.Activation('sigmoid'),
            nn.Dropout(drop_prob1), # 第一个Dropout层
            nn.MaxPool2D(pool_size=2, strides=2),
            nn.Conv2D(16, kernel_size=5),
            nn.BatchNorm(),
            nn.Activation('sigmoid'),
            nn.Dropout(drop_prob2), # 第二个Dropout层
            nn.MaxPool2D(pool_size=2, strides=2),
            nn.Dense(120),
            nn.BatchNorm(),
            nn.Activation('sigmoid'),
            nn.Dropout(drop_prob3), # 第三个Dropout层
            nn.Dense(84),
            nn.BatchNorm(),
            nn.Activation('sigmoid'),
            nn.Dropout(drop_prob4), # 第四个Dropout层
            nn.Dense(10))
    ctx = d2l.try_gpu()
    mxnet.random.seed(0) # 固定随机种子，使结果可以复现
    net.initialize(force_reinit=True, ctx=ctx, init=init.Xavier())
    # 神经网络初始化（Xavier法）
    return net

将数据分成k折

def get_k_fold_data(k, i, X, y):
    assert k > 1
    fold_size = X.shape[0] // k
    X_train, y_train = None, None
    for j in range(k):
        idx = slice(j * fold_size, (j + 1) * fold_size)
        X_part, y_part = X[idx, :], y[idx]
        if j == i:
            X_valid, y_valid = X_part, y_part
        elif X_train is None:
            X_train, y_train = X_part, y_part
        else:
            X_train = nd.concat(X_train, X_part, dim=0)
            y_train = nd.concat(y_train, y_part, dim=0)
    return X_train, y_train, X_valid, y_valid

计算批量数据的accuracy

def evaluate_accuracy(data_iter, net):
    """Evaluate accuracy of a model on the given data set."""
    acc_sum, n = nd.array([0]), 0
    for X, y in data_iter:
        y = y.reshape((1,-1))
        y = y.astype('float32')
        acc_sum += (net(X).argmax(axis=1) == y).sum()
        n += y.size
    acc_sum.wait_to_read()
    return acc_sum.asscalar() / n

训练模型

def train_ch3_modify(net, train_iter, test_iter, loss, num_epochs, batch_size,
              params=None, lr=None, trainer=None):
    """Train and evaluate a model with CPU."""
    train_ls, test_ls = [], []
    for epoch in range(num_epochs):
        train_acc_echo, n_echo = 0.0, 0.0
        for X, y in train_iter:
            with autograd.record():
                y_hat = net(X)
                l = loss(y_hat, y).sum()
            l.backward()
            if trainer is None:
                sgd(params, lr, batch_size)
            else:
                trainer.step(batch_size)
            y = y.reshape((1,-1))
            y = y.astype('float32')
            train_acc_echo += (y_hat.argmax(axis=1) == y).sum().asscalar()
            n_echo += y.size
        train_ls.append(train_acc_echo/n_echo)
        test_ls.append(evaluate_accuracy(test_iter, net))
    return train_ls, test_ls

进行k折交叉验证

def k_fold(k, X_train, y_train, num_epochs, learning_rate, weight_decay, batch_size):
    train_l_sum, valid_l_sum = 0.0, 0.0
    loss = gloss.SoftmaxCrossEntropyLoss() #采用交叉熵作为损失函数
    train_l_mean, valid_l_mean=0.0, 0.0
    transformer = []
    transformer += [gdata.vision.transforms.ToTensor()]
    transformer = gdata.vision.transforms.Compose(transformer)
    num_workers = 0
    for i in range(k):
        X_train, y_train, X_valid, y_valid = get_k_fold_data(k, i, X_train, y_train)        
        train_kfold=gdata.ArrayDataset(X_train,y_train)
        valid_kfold=gdata.ArrayDataset(X_valid,y_valid)    
        train_iter = gdata.DataLoader(train_kfold.transform_first(transformer),    
                                  batch_size, shuffle=False,
                                  num_workers=num_workers)
        valid_iter = gdata.DataLoader(valid_kfold.transform_first(transformer),
                                 batch_size, shuffle=False,
                                 num_workers=num_workers)
        
        net = get_net()
        trainer = gluon.Trainer(net.collect_params(), 'sgd', {
     'learning_rate': learning_rate, 'wd': weight_decay})
        #训练模型，返回的是各epoch下的accuracy
        train_ls, valid_ls = train_ch3_modify(net, train_iter, valid_iter, loss, num_epochs, batch_size, None,
              None, trainer)
​
        train_l_sum += train_ls[-1]
        valid_l_sum += valid_ls[-1]
        train_l_mean += np.array(train_ls)
        valid_l_mean += np.array(valid_ls)
        optimal_epoch=np.mat(valid_ls).argmax(axis=1)+1        
        print('fold %d, train acc %f, valid acc %f, optimal num_epochs %d'
              % (i, train_ls[-1], valid_ls[-1], optimal_epoch))
        
        #作图
        d2l.semilogy(range(1,num_epochs+1), train_ls, 'epochs', 'acc',
                     range(1,num_epochs+1), valid_ls,['train', 'valid'])
    
    return train_l_sum / k, valid_l_sum / k, train_l_mean / k, valid_l_mean / k

k折交叉验证实例

k, num_epochs, lr, weight_decay, batch_size = 2, 100, 0.1, 0, 100
#k为交叉验证折数，lr为learning rate
​
train_features, train_labels = mnist_train[0:5000] #为加速展示，我这里只取了前5000个cases
​
#通过交叉验证选取最优的num_epochs（耗时约388秒）
start=time.time()
train_l, valid_l, train_l_fold, valid_l_fold = k_fold(k, train_features, train_labels, num_epochs, lr,
                          weight_decay, batch_size)
​
optimal_epoch_kfold=np.argmax(valid_l_fold)+1
print('%d-fold validation: avg train acc %f, avg valid acc %f, optimal num_epochs %d'
      % (k, train_l, valid_l, optimal_epoch_kfold))
​
#作图
d2l.semilogy(range(1,num_epochs+1), list(train_l_fold), 'epochs', 'acc',
             range(1,num_epochs+1), list(valid_l_fold), ['train', 'valid'])
​
'%.2f sec' % (time.time()-start)

在卷积神经网络的卷积层和全连接层都建立Dropout层，并设置学习率为0.1（设为0.01时效果不佳），最终效果比较好。

权重衰减

  在LeNet网络的所有卷积层和全连接层之后、激活层之前加入批量归一化，并使用权重衰减。

def get_net():
    net = nn.Sequential()
    net.add(nn.Conv2D(channels=6, kernel_size=5),
        nn.BatchNorm(), # 批量归一化
        nn.Activation('sigmoid'),
        nn.MaxPool2D(pool_size=2, strides=2),
        nn.Conv2D(channels=16, kernel_size=5),
        nn.BatchNorm(),
        nn.Activation('sigmoid'),   
        nn.MaxPool2D(pool_size=2, strides=2),
        nn.Dense(120),
        nn.BatchNorm(),
        nn.Activation('sigmoid'),
        nn.Dense(84),
        nn.BatchNorm(),
        nn.Activation('sigmoid'),
        nn.Dense(10))
    ctx = d2l.try_gpu()
    mxnet.random.seed(0)
    net.initialize(force_reinit=True, ctx=ctx, init=init.Xavier())
    return net

训练模型

def train_ch3_modify(net, train_iter, test_iter, loss, num_epochs, batch_size, trainer_w, trainer_b,
              params=None, lr=None):
    """Train and evaluate a model with CPU."""
    train_ls, test_ls = [], []
    for epoch in range(num_epochs):
        train_acc_echo, n_echo = 0.0, 0
        for X, y in train_iter:
            with autograd.record():
                y_hat = net(X)
                l = loss(y_hat, y).sum()
            l.backward()
            trainer_w.step(batch_size) # 提出权重
            trainer_b.step(batch_size) # 提出偏置
            y = y.reshape((1,-1))
            y = y.astype('float32')
            train_acc_echo += (y_hat.argmax(axis=1) == y).sum().asscalar()
            n_echo += y.size
        train_ls.append(train_acc_echo/n_echo)
        test_ls.append(evaluate_accuracy(test_iter, net))
    return train_ls, test_ls

进行k折交叉验证

def k_fold_wd(k, X_train, y_train, num_epochs,
           learning_rate, weight_decay, batch_size):
    train_l_sum, valid_l_sum = 0.0, 0.0
    num_workers=0
    loss = gloss.SoftmaxCrossEntropyLoss() 
    train_l_mean, valid_l_mean=0.0, 0.0
    transformer = []
    transformer += [gdata.vision.transforms.ToTensor()]
    transformer = gdata.vision.transforms.Compose(transformer)
    for i in range(k):
        X_train, y_train, X_valid, y_valid = get_k_fold_data(k, i, X_train, y_train)        
        train_kfold=gdata.ArrayDataset(X_train,y_train)
        valid_kfold=gdata.ArrayDataset(X_valid,y_valid)    
        train_iter = gdata.DataLoader(train_kfold.transform_first(transformer),    
                                  batch_size, shuffle=False,
                                  num_workers=num_workers)
        valid_iter = gdata.DataLoader(valid_kfold.transform_first(transformer),
                             batch_size, shuffle=False,
                                 num_workers=num_workers)
        
        net = get_net()
        # 对权重进行衰减（对权重进行衰减，但对偏置不进行衰减）
        trainer_w = gluon.Trainer(net.collect_params('.*weight'), 'sgd', {
     'learning_rate': learning_rate, 'wd':weight_decay})
        trainer_b = gluon.Trainer(net.collect_params('.*bias'), 'sgd', {
     'learning_rate': learning_rate})
        #训练模型，返回的是各epoch下的accuracy
        train_ls, valid_ls = train_ch3_modify(net, train_iter, valid_iter, loss, num_epochs, batch_size, trainer_w, trainer_b, None,
              None)
        
        train_l_sum += train_ls[-1]
        valid_l_sum += valid_ls[-1]
        train_l_mean += np.array(train_ls)
        valid_l_mean += np.array(valid_ls)
        optimal_epoch=np.mat(valid_ls).argmax(axis=1)+1        
        print('fold %d, train acc %f, valid acc %f, optimal num_epochs %d'
              % (i, train_ls[-1], valid_ls[-1], optimal_epoch))
        
        #作图
        d2l.semilogy(range(1,num_epochs+1), train_ls, 'epochs', 'acc',
                       range(1,num_epochs+1), valid_ls,
                         ['train', 'valid'])
    
    return train_l_sum / k, valid_l_sum / k, train_l_mean / k, valid_l_mean / k

k折交叉验证实例

k, num_epochs, lr, weight_decay, batch_size = 2, 100, 0.01, 0.01, 100
#k为交叉验证折数，lr为learning rate
​
train_features, train_labels = mnist_train[0:5000] #为加速展示，我这里只取了前5000个cases
​
#通过交叉验证选取最优的num_epochs（耗时约388秒）
start=time.time()
train_l, valid_l, train_l_fold, valid_l_fold = k_fold_wd(k, train_features, train_labels, num_epochs, lr,
                          weight_decay, batch_size)
​
optimal_epoch_kfold=np.argmax(valid_l_fold)+1
print('%d-fold validation: avg train acc %f, avg valid acc %f, optimal num_epochs %d'
      % (k, train_l, valid_l, optimal_epoch_kfold))
​
#作图
d2l.semilogy(range(1,num_epochs+1), list(train_l_fold), 'epochs', 'acc',
             range(1,num_epochs+1), list(valid_l_fold), ['train', 'valid'])
​
'%.2f sec' % (time.time()-start)

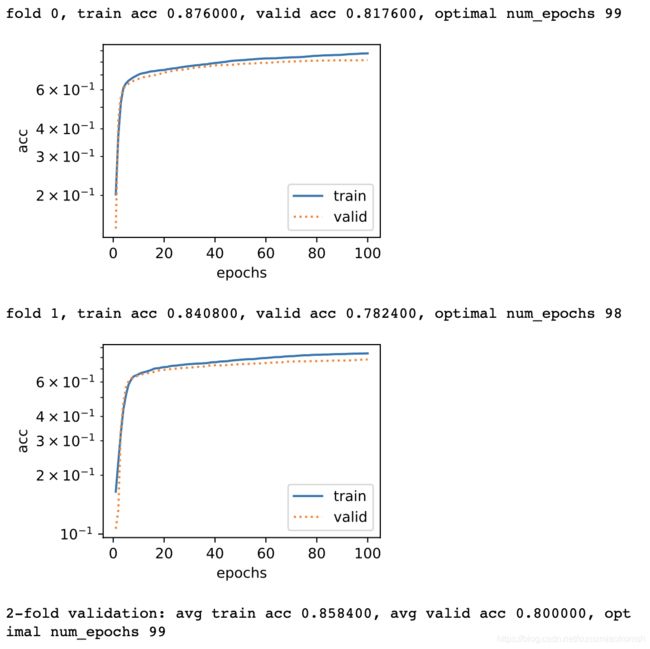
权重衰减选择学习率、权重衰减率均为0.01时，解决了过拟合问题且保证了较大的准确率。

Adam法

  在LeNet网络中使用Adam法，注意：这里不要做批量归一化，仅将k_fold的trainer中sgd改为adam，将learning rate设置为0.01。

def get_net():
    net = nn.Sequential()
    net.add(nn.Conv2D(channels=6, kernel_size=5, activation='sigmoid'),
            nn.MaxPool2D(pool_size=2, strides=2),
            nn.Conv2D(channels=16, kernel_size=5, activation='sigmoid'),
            nn.MaxPool2D(pool_size=2, strides=2),
            # Dense会默认将(批量大小, 通道, 高, 宽)形状的输入转换成
            # (批量大小, 通道 * 高 * 宽)形状的输入
            nn.Dense(120, activation='sigmoid'),
            nn.Dense(84, activation='sigmoid'),
            nn.Dense(10))
    ctx = mxnet.cpu()#修改：强行使用cpu进行运算
    mxnet.random.seed(0)
    net.initialize(force_reinit=True, ctx=ctx, init=init.Xavier())
    return net

训练模型

def train_ch3_modify(net, train_iter, test_iter, loss, num_epochs, batch_size,
              params=None, lr=None, trainer=None):
    """Train and evaluate a model with CPU."""
    train_ls, test_ls = [], []
    for epoch in range(num_epochs):
        train_acc_echo, n_echo = 0.0, 0.0
        for X, y in train_iter:
            with autograd.record():
                y_hat = net(X)
                l = loss(y_hat, y).sum()
            l.backward()
            if trainer is None:
                sgd(params, lr, batch_size)
            else:
                trainer.step(batch_size)
            y = y.reshape((1,-1))
            y = y.astype('float32')
            train_acc_echo += (y_hat.argmax(axis=1) == y).sum().asscalar()
            n_echo += y.size
        train_ls.append(train_acc_echo/n_echo)
        test_ls.append(evaluate_accuracy(test_iter, net))
    return train_ls, test_ls

进行k折交叉验证：将k_fold的trainer中sgd改为Adam。

def k_fold_adam(k, X_train, y_train, num_epochs, learning_rate, weight_decay, batch_size):
    train_l_sum, valid_l_sum = 0.0, 0.0
    loss = gloss.SoftmaxCrossEntropyLoss() #采用交叉熵作为损失函数
    train_l_mean, valid_l_mean=0.0, 0.0
    transformer = []
    transformer += [gdata.vision.transforms.ToTensor()]
    transformer = gdata.vision.transforms.Compose(transformer)
    num_workers = 0 if sys.platform.startswith('win32') else 4
    for i in range(k):
        X_train, y_train, X_valid, y_valid = get_k_fold_data(k, i, X_train, y_train)        
        train_kfold=gdata.ArrayDataset(X_train,y_train)
        valid_kfold=gdata.ArrayDataset(X_valid,y_valid)    
        train_iter = gdata.DataLoader(train_kfold.transform_first(transformer),    
                                  batch_size, shuffle=False,
                                  num_workers=num_workers)
        valid_iter = gdata.DataLoader(valid_kfold.transform_first(transformer),
                                 batch_size, shuffle=False,
                                 num_workers=num_workers)
        
        net = get_net()
        trainer = gluon.Trainer(net.collect_params(), 'adam', {
     'learning_rate': learning_rate})
        #训练模型，返回的是各epoch下的accuracy
        train_ls, valid_ls = train_ch3_modify(net, train_iter, valid_iter, loss, num_epochs, batch_size, None,
              None, trainer)
​
        train_l_sum += train_ls[-1]
        valid_l_sum += valid_ls[-1]
        train_l_mean += np.array(train_ls)
        valid_l_mean += np.array(valid_ls)
        optimal_epoch=np.mat(valid_ls).argmax(axis=1)+1        
        print('fold %d, train acc %f, valid acc %f, optimal num_epochs %d'
              % (i, train_ls[-1], valid_ls[-1], optimal_epoch))
        
        #作图
        d2l.semilogy(range(1,num_epochs+1), train_ls, 'epochs', 'acc',
                     range(1,num_epochs+1), valid_ls,['train', 'valid'])
    
    return train_l_sum / k, valid_l_sum / k, train_l_mean / k, valid_l_mean / k

k折交叉验证实例

k, num_epochs, lr, weight_decay, batch_size = 2, 100, 0.01, 0, 100
#k为交叉验证折数，lr为learning rate
​
train_features, train_labels = mnist_train[0:5000] #为加速展示，我这里只取了前5000个cases
​
#通过交叉验证选取最优的num_epochs（耗时约388秒）
start=time.time()
train_l, valid_l, train_l_fold, valid_l_fold = k_fold_adam(k, train_features, train_labels, num_epochs, lr,
                                                           weight_decay, batch_size)
​
optimal_epoch_kfold=np.argmax(valid_l_fold)+1
print('%d-fold validation: avg train acc %f, avg valid acc %f, optimal num_epochs %d'
      % (k, train_l, valid_l, optimal_epoch_kfold))
​
#作图
d2l.semilogy(range(1,num_epochs+1), list(train_l_fold), 'epochs', 'acc',
             range(1,num_epochs+1), list(valid_l_fold), ['train', 'valid'])
​
'%.2f sec' % (time.time()-start)

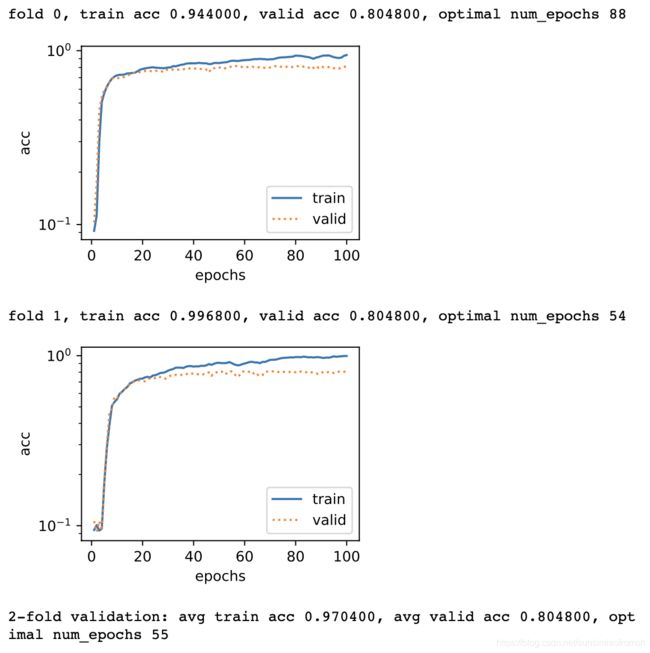
Adam算法在学习率较大时效果不太好，可能是由于下降速度太快/步长太长，如果学习率不足够小的话，可能在迭代时错过最优值或者无法收敛到最优值。改进方法是减小学习率，一般取0.001（根据《神经网络与深度学习》¹）。

参考资料

---

1. 邱锡鹏. 神经网络与深度学习[M]：13-14
   https://nndl.github.io/. ↩︎