[论文阅读]Very Low-Complexity Hardware Interleaver for Turbo Decoding
Very Low-Complexity Hardware Interleaver for Turbo Decoding
作者:Zhongfeng Wang, Senior Member, IEEE, and Qingwei Li
机构:Oregon State University, Corvallis, USA
期刊:IEEE TRANSACTIONS ON CIRCUITS AND SYSTEMS—II: EXPRESS BRIEFS
时间:JULY 2007
摘要
本文简要介绍了一种在宽带码分多址(W-CDMA)系统中实现turbo码的低复杂度硬件交织器。算法转换被广泛用于降低计算复杂度和延迟。开发了新颖的超大规模集成电路结构。硬件实现结果表明,整个turbo交织模式生成单元仅消耗4k门,比传统设计小一个数量级。
关键词
CDMA,交织器,turbo码,VLSI架构
文章目录
- Very Low-Complexity Hardware Interleaver for Turbo Decoding
-
- 摘要
- 关键词
- 一. 介绍
- 二. 基本参数的计算
-
- A. R的计算
- B. P,v和C的计算
- 三. S数组与Q数组的计算
-
- A. S数组的计算
- B. Q数组的计算
- 四. 存储P,v和Q的无效索引
-
- A. 存储P值
- B. 存储v值
- 五. 交织模式的在线计算
-
- A. 排列顺序的改变
- B. S数组索引的计算
- 六. VLSI实现
-
- A. 状态图
- B. 总体框图
- C. 实现结果
- 七. 结论
- 参考文献
一. 介绍
1993年发明的turbo码[1]由于其卓越的性能,已被第三代CDMA系统[2],[3]等多个工业标准采用。图1示出了turbo编码器结构和串行turbo解码器结构,其中 u [ k ] , x s , x p 1 u[k],x_s,x^1_p u[k],xs,xp1和 x p 2 x^2_p xp2分别代表源信息比特、系统比特、奇偶校验位-1和奇偶校验位-2; y s , y p 1 y_s,y^1_p ys,yp1和 y p 2 y^2_p yp2表示分别对应于 x s , x p 1 x_s,x^1_p xs,xp1和 x p 2 x^2_p xp2的接收软符号;RSC代表递归系统卷积编码器;软输入软输出(SISO)解码器在每个时间实例输出两个软消息:对数似然比 L R ( k ) L_R(k) LR(k)和外部信息 L e x ( k ) L_ex(k) Lex(k)。turbo码的一个关键特征是交织。在编码器端,一组信息比特被交织并发送到RSC2,以生成奇偶校验位-2。在解码器端,外部信息和 y s y_s ys符号在第二解码阶段交织[4]。在实际实现中,交织过程是通过以交错顺序读取数据来执行的(注意:去交织过程是通过将数据写回加载它们的位置来完成的。这样,去交织模式是不需要的)。因此,需要交织模式生成电路,其用作如图1所示的地址生成器。
![[论文阅读]Very Low-Complexity Hardware Interleaver for Turbo Decoding_第1张图片](http://img.e-com-net.com/image/info8/d67936f6e04a44b5a4ac8b33c5a96fbe.jpg)
在WCDMA系统中,turbo码块大小从40到5114比特不等。不同的块大小需要不同的交织模式。可以得出结论,基于只读存储器(ROM)的解决方案需要超过100M bits的存储空间来存储所有交织模式,从硬件成本的角度来看,这是不可接受的。在[5]中,Cornell宽带通信实验室的研究人员提出了一种硬件交织器解决方案。总的硬件数量约30K门。[6]中提出的基于处理器的解决方案使用了略多的硬件,同时也支持CDMA2000系统中的turbo码。
数字信号处理(DSP)系统的低功耗实现方法已在许多论文中进行了论述,如[7]。简而言之,我们最大限度地利用联合算法级、架构级和电路级超大规模集成电路优化方法来消除昂贵的乘法、除法和模运算,以降低目标系统的整体计算复杂性、计算延迟和功耗。我们的实现结果表明,所提出的设计比其他已发布的设计具有低一个数量级的硬件复杂性。
本简报组织如下。第二节描述了计算基本参数的方法。在第三节中,我们介绍了两种新的计算S和Q数组的方法,这是交织器中最复杂的两个部分。然后在第四部分,我们简要介绍一些节省存储空间的方法。在第五节中,我们提出改变排列顺序,这样可以节省一些计算硬件,并摆脱传统排列方法的延迟。第六节说明了超大规模集成电路的设计细节,并提供了实现报告。最后,第七部分得出结论。应该提到的是,通过改变第五节中讨论的排列顺序来动态生成地址的想法类似于[6]中提出的方法,尽管新的工作是独立开发的。
以下讨论中使用的大多数变量都与标准[2]中使用的符号相匹配。( N N N符合标准中的 K K K,并且, R R R符合 R R R, C C C符合 C C C, P P P符合 p p p, v v v符合 v v v, S S S符合 s s s, Q Q Q符合 q q q, U U U符合 U U U)。关于每个变量的详细定义,请参考[2]。
二. 基本参数的计算
A. R的计算
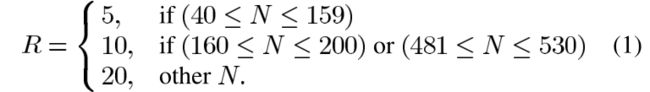
使用(1)计算行数 R R R,其中 N N N是表示块大小的输入参数。为了低复杂度的目标,我们使用3个周期进行3次比较:周期1:检查是否 N > 200 N>200 N>200,决策位表示为 D 1 D1 D1: D 1 = 1 D1=1 D1=1意味着 N > 200 N>200 N>200;周期2:检查是否 N > 480 N>480 N>480,决策位为 D 2 D2 D2;周期3:如果周期2的答案为“是”,检查 N > 530 N>530 N>530,否则检查是否 N ≥ 160 N≥160 N≥160,决策位表示为 D 3 D3 D3。可以使用基于上述三个决策位的简单组合逻辑来确定的最终值 R R R。为了降低即将到来的计算的复杂性,我们只记录了 R R R的索引: R = 5 R=5 R=5时为0, R = 10 R=10 R=10时为1以及 R = 20 R=20 R=20时为2。因此,我们只需要一个3位输入和2位输出逻辑来确定索引。
B. P,v和C的计算
第二步是确定素数 P P P和列数 C C C
![[论文阅读]Very Low-Complexity Hardware Interleaver for Turbo Decoding_第2张图片](http://img.e-com-net.com/image/info8/f631ed717b6a4ec9a40f2e10a700cc42.jpg)
基于第一步的计算结果,如果( D 3 = 0 D3=0 D3=0)且( D 2 = 1 D2=1 D2=1),则 P = 53 P=53 P=53, C = P C=P C=P。如果这个条件不满足,我们需要找到一个最小素数 P P P以致于 P ∗ R ≥ N − R P*R≥N-R P∗R≥N−R。一个常规的方法是使用二分搜索法。由于要考虑的素数总数为52(根据WCDMA标准[2,表2], P P P有52个可能值),我们需要执行6次乘法运算、6次内存访问和12次加法/减法运算来确定 P P P值。
简而言之,我们考虑一种间接计算方法。假设我们将所有 P P P值(7,11,…,257)存储在一个表中(用ROM实现,从地址“0”开始)。为了在表中寻址找到目标 P P P值,我们通过使用一些简单的映射函数来计算一个近似索引。在这里,我们构造这样的映射函数,对于任何的 N N N和 R R R它保证真实 P P P值被存储在由 P I 2 − 1 PI_2-1 PI2−1, P I 2 PI_2 PI2, P I 2 + 1 PI_2+1 PI2+1和 P I 2 + 2 PI_2+2 PI2+2索引的表的四个条目之一中。如果 P [ P I 2 ] ∗ R ≥ N − R P[PI_2]*R≥N-R P[PI2]∗R≥N−R那么检查是否 P [ P I 2 − 1 ] ∗ R ≥ N − R P[PI_2-1]*R≥N-R P[PI2−1]∗R≥N−R。如果 P [ P I 2 ] ∗ R < N − R P[PI_2]*R<N-R P[PI2]∗R<N−R那么检查是否 P [ P I 2 + 1 ] ∗ R ≥ N − R P[PI_2+1]*R≥N-R P[PI2+1]∗R≥N−R。2个时钟周期后,我们将确定目标 P P P的索引。因此,如果我们在同一条目中存储 P P P和对应的 v v v,我们可以获得 P P P值和 v v v值(与素数 P P P相关联的基元根,见标准[2,表2])。设计中使用的映射函数是分段线性函数,只需加法和移位操作就可以简单地实现。
三. S数组与Q数组的计算
A. S数组的计算
在 S [ 0 ] = 1 S[0]=1 S[0]=1时,数组 S S S计算如下:
![]()
S S S数组的直接计算将不可避免地涉及乘法和模运算,这不仅增加了硬件成本,而且增加了计算延迟。
数组的直接计算将不可避免地涉及乘法和模运算,这不仅增加了硬件成本,而且增加了计算延迟。
注意 v v v仅只有6个值:2,3,5,6,7和19。我们提出从 S [ k − 1 ] S[k-1] S[k−1]逐渐计算 S [ k ] S[k] S[k]。假设 X < P X<P X<P且 Y < P Y<P Y<P。我们有如下:
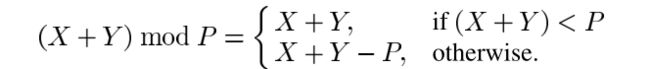
因为 S [ k − 1 ] < P S[k-1]<P S[k−1]<P, ( S [ k − 1 ] ∗ 2 m o d P ) = S [ k − 1 ] ∗ 2 (S[k-1]*2modP)=S[k-1]*2 (S[k−1]∗2modP)=S[k−1]∗2或 S [ k − 1 ] ∗ 2 − P S[k-1]*2-P S[k−1]∗2−P取决于 S [ k − 1 ] ∗ 2 < P S[k-1]*2<P S[k−1]∗2<P与否。让 X = S [ k − 1 ] ∗ 2 m o d P X=S[k-1]*2modP X=S[k−1]∗2modP, Y = S [ k − 1 ] Y=S[k-1] Y=S[k−1],我们可以用(3)计算 S [ k − 1 ] ∗ 3 m o d P S[k-1]*3modP S[k−1]∗3modP。图2显示了对于任意 v v v从 S [ k − 1 ] S[k-1] S[k−1]用于计算 S [ k ] S[k] S[k]的电路。
这种设计的基本策略是对于不同的 v v v用不同的周期数来计算不同的新值 S S S。具体来说,我们用一个周期计算 ( S [ k − 1 ] ∗ 2 ) m o d P (S[k-1]*2)modP (S[k−1]∗2)modP,两个周期计算 ( S [ k − 1 ] ∗ 3 ) m o d P (S[k-1]*3)modP (S[k−1]∗3)modP和 ( S [ k − 1 ] ∗ 4 ) m o d P (S[k-1]*4)modP (S[k−1]∗4)modP,三个周期用于 v = 5 v=5 v=5和 v = 6 v=6 v=6,四个周期用于 v = 7 v=7 v=7,且五个周期用于 v = 19 v=19 v=19。在 v = 19 v=19 v=19情况下,每次迭代需要五个周期从 S [ k − 1 ] S[k-1] S[k−1]来计算 S [ k ] S[k] S[k](即每 S S S条目需要五个周期)。在这五个周期,寄存器 D 0 D0 D0依次输出 2 ∗ S [ k − 1 ] m o d P 2*S[k-1]modP 2∗S[k−1]modP, 4 ∗ S [ k − 1 ] m o d P 4*S[k-1]modP 4∗S[k−1]modP, 6 ∗ S [ k − 1 ] m o d P 6*S[k-1]modP 6∗S[k−1]modP, 12 ∗ S [ k − 1 ] m o d P 12*S[k-1]modP 12∗S[k−1]modP和 24 ∗ S [ k − 1 ] m o d P 24*S[k-1]modP 24∗S[k−1]modP。寄存器 D 1 D1 D1依次输出 2 ∗ S [ k − 1 ] m o d P 2*S[k-1]modP 2∗S[k−1]modP, 3 ∗ S [ k − 1 ] m o d P 3*S[k-1]modP 3∗S[k−1]modP, 5 ∗ S [ k − 1 ] m o d P 5*S[k-1]modP 5∗S[k−1]modP, 7 ∗ S [ k − 1 ] m o d P 7*S[k-1]modP 7∗S[k−1]modP和 19 ∗ S [ k − 1 ] m o d P 19*S[k-1]modP 19∗S[k−1]modP。注意,这个电路只需要4个加法器和4个寄存器以及一些简单的开关/多路复用元件。多路复用器和的选择信号 S 1 S1 S1, S 2 S2 S2和 S 3 S3 S3可以从如表1所示的小查找表中产生。
![[论文阅读]Very Low-Complexity Hardware Interleaver for Turbo Decoding_第3张图片](http://img.e-com-net.com/image/info8/fcd17b9d4c3e470cba849a00df0afaf5.jpg)
B. Q数组的计算
根据标准[2], Q Q Q数组如下计算:计算 Q [ j ] , j = 1 , 2 , … , R − 1 Q[j],j=1,2,…,R-1 Q[j],j=1,2,…,R−1,使得 G C D ( Q [ j ] , P − 1 ) = 1 GCD(Q[j],P-1)=1 GCD(Q[j],P−1)=1且 Q [ j ] Q[j] Q[j]是一个素数, Q [ 0 ] = 1 , Q [ j ] > Q [ j − 1 ] Q[0]=1,Q[j]>Q[j-1] Q[0]=1,Q[j]>Q[j−1]且 Q [ j ] > 6 Q[j]>6 Q[j]>6,其中GCD代表最大公约数函数。
直接计算GCD是一个递归的过程,比执行几个除法运算还要复杂。从仿真中,我们发现数组 Q Q Q是一组序列素数 W ′ W' W′(即1,7,11,13,…,83,89)的子集。特别地,对于 P P P, Q Q Q数组的任何值,都是 R + 2 R+2 R+2序列素数 W W W的子集( W ′ W' W′的第一个 R + 2 R+2 R+2条目),其中 R R R是对应于给定 N N N值的行数。由于 Q Q Q数组恰好包含 R R R元素,我们最多需要为每个 P P P记录两个空索引。这些空索引可以很容易地从仿真中识别出来,这参考了顺序素数数组 W W W的索引,数组的条目不属于数组 Q Q Q。例如,当 P = 53 , R = 20 , P − 1 = 52 = 2 ∗ 2 ∗ 13 P=53,R=20,P-1=52=2*2*13 P=53,R=20,P−1=52=2∗2∗13,13是素数组 W W W的第四条目,而不是数组 Q Q Q的一个元素。所以空索引是3。从我们的仿真中,我们知道最大空索引是20。因此,我们需要5bits来存储一个空索引。如果没有空索引,我们存储0。只有一种情况 Q Q Q有两个空索引。当 P = 239 , R = 20 , P − 1 = 238 = 2 ∗ 7 ∗ 17 P=239,R=20,P-1=238=2*7*17 P=239,R=20,P−1=238=2∗7∗17;数组 Q Q Q中不包括两个质数7和17。因此,两个空索引是1和4。对于这种特殊情况,我们在表中存储 0 × 01 _ 100 0×01\_100 0×01_100(十进制12)。既然我们知道12不是任何其他 P P P值的空索引,我们就把它用于这种特殊情况。当然,我们可以存储另一个不用于任何情况的数字。但是这个提议的设置将导致最小的硬件成本,因为我们可以很容易地将 0 × 01 _ 100 0×01\_100 0×01_100分成 0 × 01 0×01 0×01和 0 × 100 0×100 0×100。
正如将在后面的讨论(第五节)中显示的,我们真正关心的是 Q [ j ] m o d ( P − 1 ) Q[j]mod(P-1) Q[j]mod(P−1)而不是 Q [ j ] Q[j] Q[j]它本身。我们引入了一个 Q R O M Q ROM QROM具有22个条目并存储 Q [ j ] − Q [ j − 1 ] Q[j]-Q[j-1] Q[j]−Q[j−1],即第一个条目存储1、第二个条目存储 7 − 1 = 6 7-1=6 7−1=6、第三个条目存储 11 − 7 = 4 11-7=4 11−7=4等。我们将使用以下电路进行递归计算 Q [ j ] m o d ( P − 1 ) Q[j]mod(P-1) Q[j]mod(P−1),而不引入模运算。
应该注意的是,当无效索引与运行索引 j j j匹配时,电路的输出将被丢弃。
四. 存储P,v和Q的无效索引
从上面的讨论中,很明显我们需要存储52个连续的质数 P P P,它们对应的v值,以及对应数组 Q Q Q的空索引。因为 P m a x = 257 , v m a x = 19 , Q v o i d m a x = 20 P_{max}=257,v_{max}=19,Q_{voidmax}=20 Pmax=257,vmax=19,Qvoidmax=20,一个简单的方法需要每个条目19位。但是,可以采取一些方法来节省存储空间。
A. 存储P值
最大素数257,需要9位。如果我们不存储最低有效位,我们需要8位来存储每个 P P P值。如果我们存储 P ′ = ( P − 3 ) / 2 P'=(P-3)/2 P′=(P−3)/2在表中,每个条目只需要7位。在这种情况下,我们需要一次加法和一次移位操作来恢复 P P P。更激进的方法是存储 P ′ ′ = ( P − 1 ) / 2 − 3 ∗ i + 27 P''=(P-1)/2-3*i+27 P′′=(P−1)/2−3∗i+27在表中,其中 i i i表示表中 P P P值的索引。从仿真中,我们知道 P ′ ′ P'' P′′取值从0到30。因此,对于每个 P P P我们每个只需要存储5位。我们可以从 P ′ ′ P'' P′′中按以下恢复 P P P:
![]()
上述计算涉及三个加操作和一个移位操作。在这种设计中,我们为每个条目分配8位(通过删除最低有效位),以节省恢复实际值时的进一步计算。
B. 存储v值
因为 v v v只有6个值:2、3、5、6、7和19。我们使用3位来记录 v v v的索引,即0代表2,1代表3,3代表5,4代表6,6代表7,7代表19。这里我们没有选择连续索引,原因是我们的选择是为数组 S S S的计算而优化的(参见第三节-A)。具体来说,现在通过一个简单的等式,计算 S S S数组条目的每次迭代的循环数与 v v v索引值(表示为)直接相关
![]()
其中" ≫ \gg ≫"表示右移操作。例如,当 v = 3 v=3 v=3,我们需要 ( v _ i d x + 3 ) ≫ 1 = 2 (v\_idx+3)\gg 1=2 (v_idx+3)≫1=2周期从 S [ k − 1 ] S[k-1] S[k−1]计算 S [ k ] S[k] S[k],当 v = 19 v=19 v=19时,我们需要5个周期。
正如第三节所讨论的,我们需要5位来记录每一个 P P P的无效索引。总之,我们每个条目需要 8 + 3 + 5 = 16 8+3+5=16 8+3+5=16位(如果我们每个 P P P使用5位,那么每个条目需要13位),并且我们有52个条目用于ROM。
五. 交织模式的在线计算
我们之前讨论的是重要参数( R , P , v , C , S R,P,v,C,S R,P,v,C,S数组和 Q Q Q数组)的计算,这些参数用于计算每个位的精确置换地址。这里我们称上述计算这些参数的过程为“预计算”。在本节中,我们将逐一讨论计算有效交织地址的方法。我们称这个过程为“在线计算”。实际上,我们几乎每个周期都输出一个有效的交织地址。
A. 排列顺序的改变
根据3GPP标准,在线运算顺序为:1.行内置换,2.行间置换,3.按列读出,4.删除无效位。然而,对于实际实现,这个顺序不是最有效的顺序,并且引入了不必要的硬件和计算复杂性。在随后的讨论中,我们提出了一种对较小的硬件面积和较高的速度更有效的方法。
假设输入比特流是 A 0 , A 1 , … , A N − 1 A_0,A_1,…,A_{N-1} A0,A1,…,AN−1,在插入虚拟位并按行写入后,它变成
![[论文阅读]Very Low-Complexity Hardware Interleaver for Turbo Decoding_第4张图片](http://img.e-com-net.com/image/info8/3bf17ed488834b9eb6b0cfc9d03c8489.jpg)
并且我们有关系 X i , j = A i ∗ C + j X_{i,j}=A_{i*C+j} Xi,j=Ai∗C+j。如果是 i ∗ C + j ≥ N i*C+j≥N i∗C+j≥N,那么 X i , j X_{i,j} Xi,j就是一个虚拟位。
对于行内置换,它计算参数 U i , j U_{i,j} Ui,j,该参数是第 i i i行的第 j j j置换比特的原始比特位置,如下所示
![]()
其中 γ \gamma γ数组定义为 γ T ( i ) = Q i , i = 0 , 1 , … , R − 1 \gamma_{T(i)}=Q_i,i=0,1,…,R-1 γT(i)=Qi,i=0,1,…,R−1,并且 T ( i ) i ∈ 0 , 1 , … , R − 1 T(i)_{i\in{0,1,…,R-1}} T(i)i∈0,1,…,R−1是根据不同 R R R值定义的行间置换模式[2]。行内置换后,模式变为
![[论文阅读]Very Low-Complexity Hardware Interleaver for Turbo Decoding_第5张图片](http://img.e-com-net.com/image/info8/d0beaf66dfed4a5a888718870b51474a.jpg)
其中 Y i , j = X i , U i , j Y_{i,j}=X_{i,U_{i,j}} Yi,j=Xi,Ui,j,这种操作可以表示为
![[论文阅读]Very Low-Complexity Hardware Interleaver for Turbo Decoding_第6张图片](http://img.e-com-net.com/image/info8/875901597a3a4356af9f87cda2447e65.jpg)
行间置换根据 T ( i ) T(i) T(i)对行进行置换,其中 T ( i ) T(i) T(i)是第 j j j个置换行的原始位置。行间置换后,模式变为
![[论文阅读]Very Low-Complexity Hardware Interleaver for Turbo Decoding_第7张图片](http://img.e-com-net.com/image/info8/4fbe901d6be8404b934d0f1b59cf9d04.jpg)
并且 Z i , j = Y T ( i ) , j = X T ( i ) , U T ( i ) j = A T ( i ) ∗ C + U T ( i ) j Z_{i,j}=Y_{T(i),j}=X_{T(i),U_{T(i)j}}=A_{T(i)*C+U_{T(i)j}} Zi,j=YT(i),j=XT(i),UT(i)j=AT(i)∗C+UT(i)j,行间置换可以表示为

因此,行内和行间置换可以组合为
![[论文阅读]Very Low-Complexity Hardware Interleaver for Turbo Decoding_第8张图片](http://img.e-com-net.com/image/info8/41764596fd2148f4a48fe574e8e235f4.jpg)
置换后, Z Z Z序列按列 Z 0 , 0 , Z 1 , 0 , … , Z R − 1 , 0 , Z 0 , 1 , Z 1 , 1 , … , Z R − 1 , 1 , … , Z 0 , C − 1 , … , Z R − 1 , C − 1 Z_{0,0},Z_{1,0},…,Z_{R-1,0},Z_{0,1},Z_{1,1},…,Z_{R-1,1},…,Z_{0,C-1},…,Z_{R-1,C-1} Z0,0,Z1,0,…,ZR−1,0,Z0,1,Z1,1,…,ZR−1,1,…,Z0,C−1,…,ZR−1,C−1输出。一个简单的方法是先计算 Z Z Z矩阵,存储值,然后按列读出。然而,一个更明智的方法是置换将 j j j作为外环, i i i作为内环。那么的 Z Z Z计算顺序与输出顺序相同。这样,我们可以计算一个地址,检查它是否有效(不是虚拟位),并输出它。因此,这里没有额外的存储空间为 Z Z Z且没有引入延迟。
我们的方法可以表示为
![[论文阅读]Very Low-Complexity Hardware Interleaver for Turbo Decoding_第9张图片](http://img.e-com-net.com/image/info8/96a11b1a999f4dc3970900bd23b9db40.jpg)
我们在实现中使用了这种更快的方法。另一件值得注意的事情是:在排列顺序改变之后, U i , j U_{i,j} Ui,j的计算变成了计算 U T ( i ) j U_{T(i)j} UT(i)j。根据(6),我们有
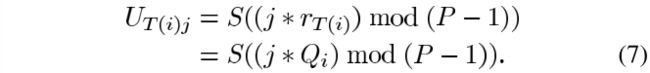
因此,我们的转换的另一个好处是:我们避免了计算数组 γ \gamma γ的步骤,这既节省了计算时间,也节省了存储 γ \gamma γ值所需的内存。应该提到的是[6]中基于处理器的turbo交织器设计以类似的方式改变了排列顺序,以降低复杂性。
B. S数组索引的计算
注意在(7)中,为了计算 U U U, S I d x = ( j ∗ Q i ) m o d ( P − 1 ) SIdx=(j*Q_i)mod(P-1) SIdx=(j∗Qi)mod(P−1)是需要的,这里 S I d x SIdx SIdx表示 S S S索引。图4展示了我们用来计算 S S S索引的电路。为了避免乘法运算,我们递归地从 S I d x ( i , j − 1 ) SIdx(i,j-1) SIdx(i,j−1)计算 S I d x ( i , j ) SIdx(i,j) SIdx(i,j)
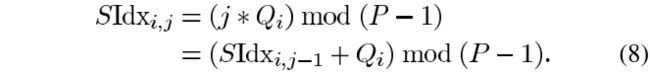
![[论文阅读]Very Low-Complexity Hardware Interleaver for Turbo Decoding_第10张图片](http://img.e-com-net.com/image/info8/97f6af2762ce49f69cd80505025fa7f6.jpg)
![[论文阅读]Very Low-Complexity Hardware Interleaver for Turbo Decoding_第11张图片](http://img.e-com-net.com/image/info8/c51de9ca9e9c4cc6af95d5ff8cea92bd.jpg)
因此,根据这个等式,数组 Q Q Q的值在保存和使用之前需要取模 P − 1 P-1 P−1。这就是为什么我们设计图3中的电路来计算 Q Q Q的原因。应该指出的是,类似于(8)的增量计算已经在[6]中看到。然而,这部分工作是由第一作者独立开发的。
六. VLSI实现
A. 状态图
B. 总体框图
图6示出了turbo交织器地址生成器的总体框图,其中 N N N是turbo码块大小。 T a s k _ b e g i n Task\_begin Task_begin号指示计算开始, t a s k _ k i l l task\_kill task_kill信号强制任务停止并返回空闲状态。信号“ a d d r e s s address address”是交错地址输出。“ a d d r e s s v a l i d address valid addressvalid”表示输出地址是否来自虚拟位。“ I n d e x Index Index”代表计算输入位的地址。例如, i n d e x = 0 , a d d r e s s = 33 index=0,address=33 index=0,address=33表示第一位将被交织到第34位。 S _ R A M S\_RAM S_RAM、 Q _ a r r a y Q\_array Q_array和 S I d x _ a r r a y SIdx\_array SIdx_array是分别用于存储阵列 S S S、阵列 Q Q Q和阵列 S I n d e x SIndex SIndex的RAMs。 T _ R O M T\_ROM T_ROM存储行间置换模式 T T T。 p v Q R O M pvQ_ROM pvQROM存储 P , v P,v P,v的值和数组 Q Q Q的空索引。 Q R O M Q_ROM QROM存储22个微分素数序列。计算核心包含主有限状态机和其他组合和时序逻辑,以进行控制和计算。
![[论文阅读]Very Low-Complexity Hardware Interleaver for Turbo Decoding_第13张图片](http://img.e-com-net.com/image/info8/48136fd1aad34c84bce5b153ff9ce3a6.jpg)
C. 实现结果
请参考表2和表3。上面讨论的架构已经使用 V e r i l o g Verilog Verilog硬件描述语言进行了建模。通过将输出结果与C程序进行比较,对设计逻辑进行了仿真和验证。我们进行了综合、优化和布局布线。综合的目标是SMIC 0.18μm标准CMOS工艺。优化目标设置为面积。总硬件成本约为4.03门。最大时钟频率为130 MHz。所需的时钟频率为 2 M ∗ 6 ∗ 2 = 24 M H z 2 M * 6 * 2 = 24 MHz 2M∗6∗2=24MHz,其中我们假设对turbo解码执行六次迭代。这意味着我们设计中真正的关键路径比要求的要短得多。因此,我们可以使用明显更低的电源电压来驱动电路,以便二次降低功耗。简而言之,与[5]和[6]中给出的设计相比,所提出的设计在面积和功耗方面都要高效一个数量级。
![[论文阅读]Very Low-Complexity Hardware Interleaver for Turbo Decoding_第14张图片](http://img.e-com-net.com/image/info8/6c1bda8f991445f18537def4130111dc.jpg)
![[论文阅读]Very Low-Complexity Hardware Interleaver for Turbo Decoding_第15张图片](http://img.e-com-net.com/image/info8/0f1ae4f52468494d9d8864a669e74838.jpg)
七. 结论
在这篇文章中,我们提出了一种新的硬件交织器结构和3G WCDMA系统的实现。各种优化技术,特别是明智的算法转换和新颖的超大规模集成电路架构,已经被引入并应用于这一设计。实现结果证明了这些技术的好处,并表明这种设计比现有技术的效率高一个数量级。
![[论文阅读]Very Low-Complexity Hardware Interleaver for Turbo Decoding_第12张图片](http://img.e-com-net.com/image/info8/7571585dba8949f28fd5597010a64e49.jpg)
![[论文阅读]Very Low-Complexity Hardware Interleaver for Turbo Decoding_第16张图片](http://img.e-com-net.com/image/info8/cddbea91e7864e898410db3469aae353.jpg)