ADT: Red-Black Tree 红黑树详解(附完整实现)
ADT: Red-Black Tree 红黑树详解(附完整实现)
文章目录
- ADT: Red-Black Tree 红黑树详解(附完整实现)
-
- 简介
- 参考
- 完整示例代码
- 正文
-
- 红黑树的前身今世
-
- 从 BST 到 AVL
- 从 AVL 到 RB-Tree
- 红黑树的规则
- 代码实现
-
- 操作接口
- Color 颜色定义 & Node 节点结构 & 初始化
- 工具方法
-
- Rotate 旋转
- Relative 查找亲戚
- Tansplant 取代
- `height()` 获取树的黑高
- `insert(K key, T data)` 插入节点
-
- 红黑树插入总结
- 红黑树插入样例
- `delete(K key)` 删除节点
-
- 红黑树删除总结
- 红黑树删除样例
- 结语
简介
- 前置文章:
- ADT: Binary-Search-Tree 二叉搜索树
- ADT: AVL Tree 平衡二叉搜索树(附Java实现)
要先了解红黑树到底是什么、红黑树的规则&特性、使用红黑树带来的好处等,势必要先了解红黑树的基础 BST 二叉搜索树(Binary Search Tree),以及直接根据树高进行平衡的 AVL Tree 平衡二叉搜索树。如果还不知道这些都是个啥的读者可以先参考上面的两篇博客。下面我们就开始细细的品味大名鼎鼎的 RB-Tree 红黑树(Red-Black Tree) 吧。
参考
| 算法导论-原书第三版 |
完整示例代码
https://github.com/superfreeeee/Blog-code/tree/main/adt_algorithm/src/main/java/adt/tree/rb
正文
红黑树的前身今世
在开始讲解红黑树是如何运行的之前,我们先来看看红黑树的基础 BST 以及与红黑树类似的目标都是对 BST 进行平衡的 AVL 树
从 BST 到 AVL
首先我们要先知道,红黑树是一种基于 BST(二叉搜索树)的变体,是对 BST 进行平衡的其中一种解决方案。因此在进入红黑树之前我们先来看看另一个更广为人知的平衡方案:平衡二叉搜索树(AVL 树)
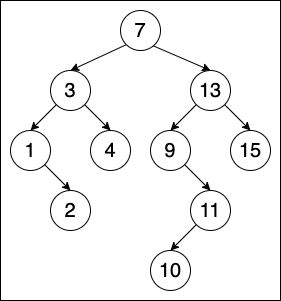
下图为二叉搜索树的一个实例
二叉搜索树的规则详细大家都了如指掌,所有节点都必须满足:左节点的键值 < < < 根结点的键值 < < < 右结点的键值。
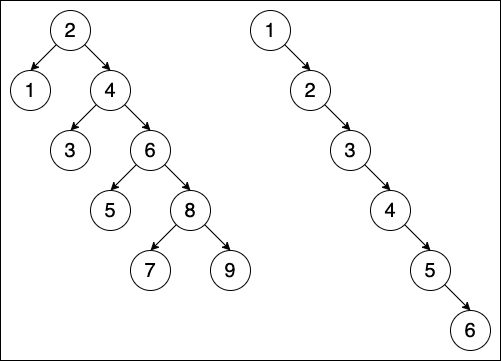
在此基础之上已经能很好的简化一个数据集合的查找时间为 O ( log 2 n ) O(\log_{2}{n}) O(log2n),然而当出现下列极端情况(不平衡)的时候:
二叉搜索树的性能就会逐渐降低,甚至如上面右图整棵树已经变形成一个链表,查找的时间复杂度降低到 O ( n ) O(n) O(n),会出现这样的问题是因为树的 不平衡。
我们知道根据二叉树的定义一个节点至多可以存在两个子节点(左、右),而树节点相关的操作复杂度都是与树的高度相关的,因此在以 最小化所有节点到根结点的路径和 为目标的前提之下,我们可以透过考察树的 平衡因子(balance factor,左右子树的高度差) 来确保各个节点尽量的向根结点靠拢。
AVL 树的规则就是确保 所有节点的平衡因子不大于 1 来实现二叉搜索树的平衡,实现时可以透过**旋转(Rotate)**的手段在插入和删除节点之后检查并恢复整棵树的平衡,如下便是一个按 1 , 2 , 3 , 4 , 5 , 6 , 7 1, 2, 3, 4, 5, 6, 7 1,2,3,4,5,6,7 的顺序插入建立 AVL 树的实例(红色节点的左右数字表示两侧子树的高度,蓝色为平衡后的新的局部根节点)
我们可以看到最终结果 AVL 很好的平衡了二叉搜索树的节点,非常有效的限制了树高的增长。
从 AVL 到 RB-Tree
然而如同 AVL 一般的平衡树我们还是不太满意,不是因为不够平衡,反而是因为太过平衡了。在实践中我们发现 AVL 的平衡条件过于严格,使得频繁的插入、删除操作将大幅影响性能。
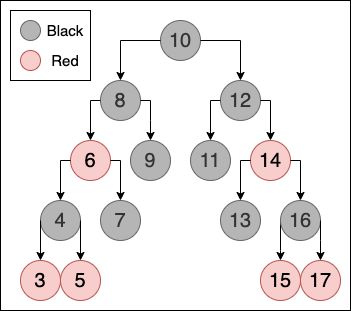
因此就有人提出 RB-Tree 红黑树 的概念,延续 AVL 对’高度’进行平衡的思想,透过对节点进行着色( R e d Red Red or B l a c k Black Black),并只对 黑高(bh = black height,路径上黑节点的个数) 进行平衡,对平衡条件进行适度的放宽,对于高度的限制也在容许的范围之内。如下图就是一个红黑树的实例,具体的规则后面会再详细说明。
红黑树的规则
了解我们为什么要用红黑树之后,马上就来看看红黑树的性质。
一棵 BST 要成为一个红黑树总共需要满足四个条件:
- 每个节点必须是 黑色( B l a c k Black Black) 或是 红色( R e d Red Red)
- 根( r o o t root root)结点为黑色
- 红色节点的两个子节点必须为黑色
- 从根节点到叶节点的所有路径都有相同数量的黑色节点(即黑高 bh = black height)
- 边界条件处理:为了方便处理空指针问题,我们定义一个 N I L NIL NIL 的黑色节点来替代所有的 NULL 空指针
性质 3、4 就说明了红黑树的平衡条件限制:所有路径的黑高相等,同时红节点的子节点必为黑色(不可能连续出现两个红色),说明 最长路径必小于等于最短路径的两倍,这就是红黑树的平衡条件核心。
代码实现
光说不练成不了气候,马上就带大家来实现一个红黑树数据结构(使用 Java 实现)
操作接口
养成良好的编程习惯,面对接口编程。所以这边我们先来定义红黑树的操作接口:
Tree.java:树的通用接口
package adt.tree;
/* 树 */
public interface Tree<K extends Comparable<K>, T> {
/* 插入节点 */
void insert(K key, T data);
/* 删除节点 */
T delete(K key);
/* 返回树高 */
int height();
/* 检查树是否为空 */
boolean empty();
/* 返回节点数量 */
int nodes();
/* 先序遍历 */
void preorder();
/* 中序遍历 */
void inorder();
/* 后序遍历 */
void postorder();
/* 层序遍历 */
void layerorder();
}
BinarySearchTree.java:二叉搜索树接口
package adt.tree.bst;
import adt.tree.Tree;
/* 二叉搜索树 */
public interface BinarySearchTree<K extends Comparable<K>, T> extends Tree<K, T> {
/* 根据键查找元素 */
T search(K key);
/* 查找键最小的元素 */
T minimum();
/* 查找键最大的元素 */
T maximum();
/* 查找给定键的前驱元素 */
T predecessor(K key);
/* 查找给定键的后继元素 */
T successor(K key);
/* 展示树形结构 */
void tree();
}
RedBlackTree.java:红黑树接口
package adt.tree.rb;
import adt.tree.bst.BinarySearchTree;
public interface RedBlackTree<K extends Comparable<K>, T> extends BinarySearchTree<K, T> {
/* 检查红黑树性质 */
void validate();
}
由于博主还有实现其他树的抽象结构,所以自己建立了一个抽象接口的体系,有可能会在之后进行对应的修改,实际最终成果以 github 仓库为准。
红黑树的对外接口中,大部分的操作几乎与二叉搜索树类似,所以这边就不再详细展开,有兴趣可以到代码仓库查看完整版。本篇只会着重解释 height、insert、delete 等操作的实现。
Color 颜色定义 & Node 节点结构 & 初始化
有了操作接口之后,我们先定义好内部节点类
private static final boolean RED = false, BLACK = true;
private static class Node<K, T> {
K key;
T data;
boolean color;
Node<K, T> left;
Node<K, T> right;
Node<K, T> parent;
public Node(K key, T data) {
this.key = key;
this.data = data;
this.color = RED;
}
@Override
public String toString() {
return "{" + key + "(" + (color ? "Black" : "Red") + "):" + data + "}";
}
}
private Node<K, T> NIL;
private Node<K, T> root;
public RedBlackTreeImpl() {
NIL = new Node<>(null, null);
NIL.color = BLACK;
root = NIL.parent = NIL.left = NIL.right = NIL;
}
-
颜色我们使用布尔值来表示:
true为 B L A C K BLACK BLACK、false为 R E D RED RED -
内部节点结构:
- key 键值
- data 附带数据
- color 节点颜色
- left 左子节点
- right 右子节点
- parent 父节点
-
初始化:在构造函数内部初始化 N I L NIL NIL 空节点和 r o o t root root 根结点的指针
工具方法
在开始具体的实现之前,我们先来介绍几个后续操作中会用到的私有工具方法
Rotate 旋转
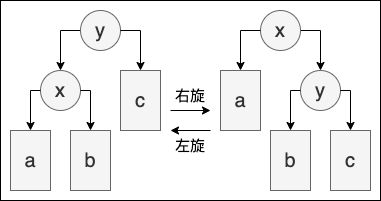
首先第一个最重要的当然是要能够进行树节点的旋转,不管是 AVL 还是 RB-Tree 都是一个极为重要且核心的操作。直接上图
简而言之就是将 x − y x-y x−y 两个节点向左/向右进行旋转,并将较低的节点的内侧子节点接到另一个节点身上。
// 左旋转
private void leftRotate(Node<K, T> x) {
// y x
// / \ / \
// x c <- a y
// / \ / \
// a b b c
Node<K, T> y = x.right;
// y & x.p
y.parent = x.parent;
if (x == root) root = y;
else if (x == x.parent.left) x.parent.left = y;
else x.parent.right = y;
// x & y.left
x.right = y.left;
if (x.right != NIL) x.right.parent = x;
// x & y
y.left = x;
x.parent = y;
}
// 右旋转
private void rightRotate(Node<K, T> y) {
// y x
// / \ / \
// x c -> a y
// / \ / \
// a b b c
Node<K, T> x = y.left;
// x & y.p
x.parent = y.parent;
if (y == root) root = x;
else if (y == y.parent.left) y.parent.left = x;
else y.parent.right = x;
// y & x.right
y.left = x.right;
if (y.left != NIL) y.left.parent = y;
// x & y
x.right = y;
y.parent = x;
}
Relative 查找亲戚
由于后续操作有很多是左右对称的,为了避免重复相似的代码,我把它简化成几个相对关系而左右无关的查找亲戚节点的方法
uncle叔节点:父节点的父节点的另一个子节点(自己体会吧hhh)brother兄弟节点:父节点的另一个子节点innerChild内侧子节点:所谓的内侧是相对与与父节点的关系,即所谓的 L R 、 R L LR、RL LR、RL 两种节点outerChild外侧子节点:就是内侧的另一个子节点,即 L L 、 R R LL、RR LL、RR
/* 叔节点 */
private Node<K, T> uncle(Node<K, T> node) {
if (node.parent == NIL || node.parent.parent == NIL) return NIL;
if (node.parent == node.parent.parent.left) return node.parent.parent.right;
return node.parent.parent.left;
}
/* 兄弟节点 */
private Node<K, T> brother(Node<K, T> x) {
if (x.parent == NIL) return NIL;
return x == x.parent.left ? x.parent.right : x.parent.left;
}
/* 内侧子节点:LR、RL */
private Node<K, T> innerChild(Node<K, T> x) {
return x == x.parent.right ? x.left : x.right;
}
/* 外则子节点:LL、RR */
private Node<K, T> outerChild(Node<K, T> x) {
return x == x.parent.left ? x.left : x.right;
}
Tansplant 取代
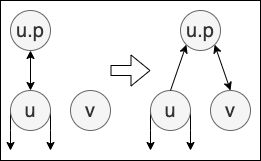
最后一种是 delete 操作时会用到的辅助操作,transplant 用于建立 u.p 和 v 节点之间的联系(使 u.p 指向 u 的指针指向 v,并且 v.p 指向 u.p)
/* v 与 u.p 之间的联系 */
private void transplant(Node<K, T> u, Node<K, T> v) {
if (u.parent == NIL) root = v;
else if (u == u.parent.left) u.parent.left = v;
else u.parent.right = v;
v.parent = u.parent;
}
height() 获取树的黑高
首先第一个先把简单的解决了:获取树的黑高。
思路:黑高为子树中较高的树 + 自己的高度(遇到黑节点 + 1)。
@Override
public int height() {
return height(root);
}
private int height(Node<K, T> node) {
if (node == NIL) return 0;
int L = height(node.left);
int R = height(node.right);
int h = Math.max(L, R) + (node.color == BLACK ? 1 : 0);
return h;
}
insert(K key, T data) 插入节点
下面我们就要进入红黑树的重头戏了,首先我们从插入开始。
向红黑树插入节点的操作可以分成前后两个步骤:
- 第一步
insert:与一般的二叉搜索树一样,根据键值将新的数据节点插入到合适的位置- 新的节点起始为红色
- 新的节点的
parent、left、right指针初始都指向 N I L NIL NIL 空节点
代码与简单 BST 的几乎一样
@Override
public void insert(K key, T data) {
Node<K, T> node = createNode(key, data);
Node<K, T> pre = NIL, cur = root;
while (cur != NIL) {
pre = cur;
cur = key.compareTo(cur.key) <= 0 ? cur.left : cur.right;
}
node.parent = pre;
if (pre == NIL) {
root = node;
} else if (key.compareTo(pre.key) <= 0) {
pre.left = node;
} else {
pre.right = node;
}
insertFixUp(node);
}
- 第二步
insertFixUp(x):在第二步中我们需要对插入的节点进行颜色的修正,由于新插入的节点必为红色,所以并不会影响黑高,所以唯一会破坏的条件只有 性质 3:红节点的孩子必为黑节点,也就是插入节点的父节点为红色的情况
在这样的场景之下,我们可以将需要修正的情形划分为三种情况:
-
条件假设:
- 插入的新节点为
z bh表示的子树黑高一律不算上灰节点 any 的高度(不影响结果- 假设整棵子树的黑高为
h
- 插入的新节点为
-
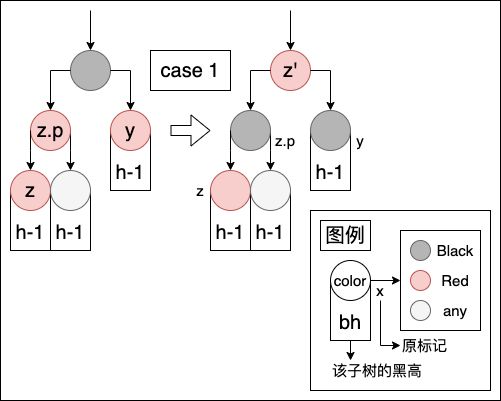
c a s e 1 case \space 1 case 1:插入节点
z的叔节点y为红色
这时候我们可以看到图中 z.p.p 的两个子节点都为红色(由于插入前符合红黑树性质,所以 z.p.p 必为黑色,才不会与 z.p 的红色冲突),因此我们可以将 z.p.p 的黑色下降一层,将 z.p 和 y 都变为红色,并将 z.p.p 变为红色,之后再从 z' = z.p.p 出发继续向上修正
/* insertFixUp - case 1 */
Node<K, T> y = uncle(z);
if (y.color == RED) {
// ?:B ?:R
// / \ / \
// ?:R y:R -> ?:B ?:B
// / /
// z:R z:R
// case 1
z.parent.color = y.color = BLACK;
y.parent.color = RED;
z = y.parent;
continue;
}
-
c a s e 2 、 3 case \space 2、3 case 2、3:插入节点
z的叔节点y为 黑色c a s e 2 、 3 case 2、3 case2、3 为 c a s e 1 case 1 case1 的反例,而 c a s e 2 case 2 case2 变换后的情形正好是 c a s e 3 case 3 case3 适用的情形,先上图
-
c a s e 2 case 2 case2:插入节点
z的叔节点y为 黑色,且插入节点属于内侧节点在 c a s e 2 case 2 case2 的场景之下,我们只需要进行一次单旋,将作为内侧节点的
z向外旋转,并将z设置为旋转后的新的外侧节点,进入 c a s e 3 case 3 case3 -
c a s e 3 case 3 case3:插入节点
z的叔节点y为 黑色,且插入节点属于外侧节点对于 c a s e 3 case 3 case3,我们知道
z'和z'.p都是红色,而位于最下层的a、b、c、y的黑高都是 h − 1 h-1 h−1,因此我们可以透过一次旋转使得节点能更均匀的分布在y.p的两侧
-
/* insertFixUp - case 2 & 3 */
if (z == innerChild(z)) {
// ?:B ?:B
// / \ / \
// ?:R ?:B -> z:R ?:B
// \ /
// z:R ?:R
// case 2
if (z == z.parent.right) {
leftRotate(z.parent);
z = z.left;
} else {
rightRotate(z.parent);
z = z.right;
}
}
// case 3
// b:B a:B
// / \ / \
// a:R c:B -> z:R b:R
// / \
// z:R ?:B
z.parent.color = BLACK;
z.parent.parent.color = RED;
if (z == z.parent.left) {
rightRotate(z.parent.parent);
} else {
leftRotate(z.parent.parent);
}
红黑树插入总结
- 处理过程:分成两步骤
- 节点插入
insert:基本 BST 的插入 - 颜色修正
insertFixUp:对插入节点进行旋转、变色来维持红黑性质。分成三种情况
- 节点插入
| 场景 | 处理方式 | |
|---|---|---|
| c a s e 1 case 1 case1 | 插入节点 z 的叔节点 y 为红色 |
将 z.p.p 的黑色降层到 z.p 和 y,并将 z.p.p 变色为红色后继续新一轮的修正 |
| c a s e 2 case 2 case2 | 插入节点 z 的叔节点 y 为 黑色,且插入节点属于内侧节点 |
将作为内侧的 z 节点向外单旋,并以新的外侧节点(也就是原来的 z.p)作为新的 z 进入 c a s e 3 case 3 case3 |
| c a s e 3 case 3 case3 | 插入节点 z 的叔节点 y 为 黑色,且插入节点属于外侧节点 |
底层的四个子树黑高相等,以 z.p.p 进行一次单旋来平衡两侧的节点数量 |
- 完整插入实现
@Override
public void insert(K key, T data) {
Node<K, T> node = createNode(key, data);
Node<K, T> pre = NIL, cur = root;
while (cur != NIL) {
pre = cur;
cur = key.compareTo(cur.key) <= 0 ? cur.left : cur.right;
}
node.parent = pre;
if (pre == NIL) {
root = node;
} else if (key.compareTo(pre.key) <= 0) {
pre.left = node;
} else {
pre.right = node;
}
insertFixUp(node);
}
/* 插入修正 */
private void insertFixUp(Node<K, T> z) {
while (z.parent.color == RED) {
Node<K, T> y = uncle(z);
// case 1
if (y.color == RED) {
// ?:B ?:R
// / \ / \
// ?:R y:R -> ?:B ?:B
// / /
// z:R z:R
z.parent.color = y.color = BLACK;
y.parent.color = RED;
z = y.parent;
continue;
}
// case 2
if (z == innerChild(z)) {
// ?:B ?:B
// / \ / \
// ?:R ?:B -> z:R ?:B
// \ /
// z:R ?:R
if (z == z.parent.right) {
leftRotate(z.parent);
z = z.left;
} else {
rightRotate(z.parent);
z = z.right;
}
}
// case 3
// b:B a:B
// / \ / \
// a:R c:B -> z:R b:R
// / \
// z:R ?:B
z.parent.color = BLACK;
z.parent.parent.color = RED;
if (z == z.parent.left) {
rightRotate(z.parent.parent);
} else {
leftRotate(z.parent.parent);
}
}
root.color = BLACK;
}
最后的最后由于我们可能从 c a s e 1 case 1 case1 的场景将 r o o t root root 变为红色,因此需要在修正的最后每次都强制变为黑色(这也是红黑树高度增长的唯一途径,黑高是从根结点增加而来的)
红黑树插入样例
第一个箭头为第一步,后面多次操作为第二步的循环;z 为检查节点基准,y 保持为 z 的叔节点
delete(K key) 删除节点
第二个重要操作则是红黑树的删除节点操作,与插入相似的是它也分成两个步骤:
- 第一步
delete:与二叉搜索树一般,找到替代的子节点 or 后继节点进行替换。与二叉树不同的是用于替换的节点还需要继承将要删除的节点的颜色
@Override
public T delete(K key) {
Node<K, T> z = search(root, key), x;
if (z == NIL) return null;
boolean originColor = z.color;
if (z.left == NIL) {
x = z.right;
transplant(z, z.right);
} else if (z.right == NIL) {
x = z.left;
transplant(z, z.left);
} else {
Node<K, T> y = minimum(z.right); // 找后继
originColor = y.color;
x = y.right; // 后继必无左子
if (y.parent == z) {
x.parent = z;
} else {
transplant(y, y.right);
y.right = z.right;
y.right.parent = y;
}
transplant(z, y);
y.left = z.left;
y.left.parent = y;
y.color = z.color;
}
if (originColor == BLACK) {
deleteFixUp(x);
}
return z.data;
}
这边要特别注意,与插入不同的是,并不是每次删除都需要进行修正。我们将要删除的节点的颜色记录在 originColor,只有在 originColor == BLACK 的时候,才会影响到黑高,进而才需要进行删除后的调整。
- 第二步
deleteFixUp:若删除的节点为黑色,则会影响到该节点以下的子树的黑高异常,所以我们需要根据四种不同的情况进行删除后的调整。
-
删除后的修正前提
- 删除后需要进行调整 → \to → 删除的原节点为黑色 → \to → 修正开始后标记为
x的节点会隐式的附带一重黑色 - 删除后节点原位置标记为
x,x的兄弟节点标记为w x节点处理进入修正时附带隐式的一重黑色,本身也必须是黑色,否则可以跳出循环直接对x进行涂黑
- 删除后需要进行调整 → \to → 删除的原节点为黑色 → \to → 修正开始后标记为
-
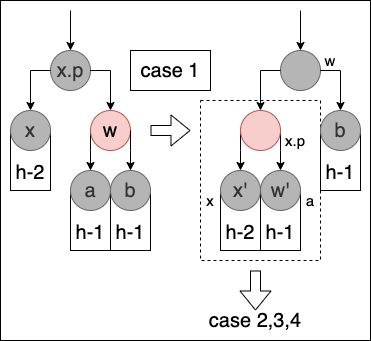
c a s e 1 case 1 case1:原位置节点
x的兄弟节点w为红色
遇到该情况的时候,由于 x 多附带一重黑色,所以我们可以透过将 w 向 x 的那一侧进行一次旋转,使得 x 节点下降一层, w 的黑色内侧节点(w 为红色)成为 x 的新的兄弟节点,进而变成 c a s e 2 、 3 、 4 case 2、3、4 case2、3、4 的情况
/* deleteFixUp - case 1 */
Node<K, T> w = brother(x);
if (w.color == RED) {
// ?:B w:B
// / \ / \
// x:B w:R -> ?:R b:B
// / \ / \
// a:B b:B x:B a:B
w.color = BLACK;
x.parent.color = RED;
leftRotate(x.parent);
w = brother(x);
}
- c a s e 2 、 3 、 4 case 2、3、4 case2、3、4:原位置节点
x的兄弟节点w为黑色
下面我们从 c a s e 2 case 2 case2 开始讲解
- c a s e 2 case 2 case2:原位置节点
x的兄弟节点w为黑色,w的两个子节点皆为黑色
在该情况下,由于 x 本身代表着二重黑色,我们可以透过将 w 的黑色与 x 的其中一重黑色一并提升到 x.p,也就是使 x.p 作为新的 x 开始新的一轮修正。
/* deleteFixUp - case 2 */
if (w.left.color == BLACK && w.right.color == BLACK) {
// ?:R ?:R
// / \ / \
// x:B w:B -> x:B w:R
// / \ / \
// a:B b:B a:B a:B
w.color = RED;
x = x.parent;
}
- c a s e 3 case 3 case3:原位置节点
x的兄弟节点w为黑色,w的外侧子节点皆为黑色 - c a s e 4 case 4 case4:原位置节点
x的兄弟节点w为黑色,w的外侧节点皆为红色
当我们遇到 c a s e 3 case 3 case3 的时候可以透过对 w 向外侧进行一次旋转来变为 c a s e 4 case 4 case4 的情形。而对于 c a s e 4 case 4 case4 同样由于 x 代表着二重的黑色,我们对 x.p 向 x 这一侧进行旋转之后,并使 x.p 涂黑以代表 x 所代表的额外一重的黑色,另外我们将仍旧处于子树同一侧的 b 涂黑,视为继承了原来 w 位置的黑色,以维持左右两侧的黑高不变。
经过 c a s e 4 case 4 case4 的操作之后,x 所附带的隐式的一重黑色已经被完全消除,所以我们就可以透过将 x 置为 r o o t root root 来跳出循环
/* deleteFixUp - case 3 & 4 */
if (outerChild(w).color == BLACK) {
// ?:R ?:R
// / \ / \
// x:B w:B -> x:B w:R
// / \ / \
// a:R b:B a:B a:B
// case 3
innerChild(w).color = BLACK;
w.color = RED;
if (w == w.parent.right) {
rightRotate(w);
} else {
leftRotate(w);
}
w = brother(x);
}
// case 4
// ?:? w:?
// / \ / \
// x:B w:B -> ?:B b:B
// / \ / \
// a:? b:R x:B a:?
w.color = x.parent.color;
x.parent.color = BLACK;
outerChild(w).color = BLACK;
if (w == w.parent.right) {
leftRotate(x.parent);
} else {
rightRotate(x.parent);
}
x = root;
红黑树删除总结
最后我们一样对删除进行一个总结,删除一样分成 2 个步骤,第二个步骤分成 4 种情况
-
两个步骤
- 节点删除
delete:找到能替代删除节点的空位 - 黑色回填
deleteFixUp:修正删除黑色节点后多出来的一重黑色
- 节点删除
-
四种情况
| 场景 | 处理方式 | |
|---|---|---|
| c a s e 1 case 1 case1 | 原位置节点 x 的兄弟节点 w 为红色 |
对 x.p 向 x 的一侧进行单旋使得 x 的新的兄弟 w' 为 w 的内侧黑色子节点(由于 w 为红色),而进入 c a s e 2 、 3 、 4 case 2、3、4 case2、3、4 |
| c a s e 2 case 2 case2 | 原位置节点 x 的兄弟节点 w 为黑色,w 的两个子节点皆为黑色 |
将 w 与 x 的一重黑色共同上升到 x.p,即将 w 变色为红色并将 x.p 作为新的 x 来隐式的附带一重黑色 |
| c a s e 3 case 3 case3 | 原位置节点 x 的兄弟节点 w 为黑色,w 的外侧子节点皆为黑色 |
透过对 w 向外侧进行一次单旋来变为 c a s e 4 case 4 case4 |
| c a s e 4 case 4 case4 | 原位置节点 x 的兄弟节点 w 为黑色,w 的外侧节点皆为红色 |
透过对 x.p 向 x 一侧进行旋转,并将 x.p 涂黑来代表 x 附带的隐式的一重黑色,原来的 w 的外侧节点也进行涂黑来代表继承原来的 w 的黑色,到此完成 x 多出来的一重黑色的回填 |
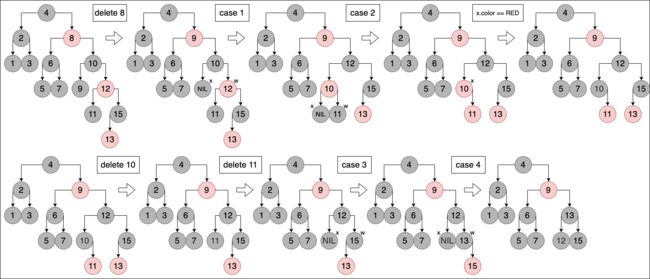
红黑树删除样例
进行两次删除操作,先删除 8 时分别经历 c a s e 1 、 2 case 1、2 case1、2,再删除 10、11 时经历 c a s e 3 、 4 case 3、4 case3、4。图中维持 x 表示删除节点的原位置,w 为 x 的兄弟节点
结语
本篇算是博主的一个突破,尝试着写了一个相对较为复杂的一篇数据结构。大名鼎鼎的红黑树算是面试题的常客,也是实际产品实践的时候能够选用的一个应用技术之一。不管是为了面试而准备,或是纯粹精进自己的数据结构基础功底,都推荐大家动手画画图,写不出完整详细的红黑树实现,至少要知道它的原理才不会误用嘛!