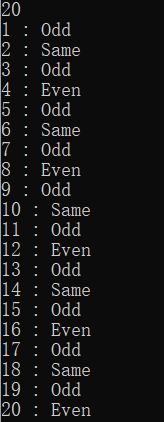大连海事大学ACM校赛题解
大连海事大学ACM校赛题解
感谢xzx对题目的排版~
作为出题人之一，我先简单说一下我认为的题目难度。
我觉着第一档比较容易的签到题是L、J、M，L就是向下取整的签到；J是简单思维、构造题，到了6以后，都可以按3,6,2,4,8…这样组成<3,6>,<6,2>,<2,4>,<4,8>这样来符合题意；M可以打个1-20的表，也可以简单手推，比较容易看出的规律；然后A题本来是第二档的，但是后来发现好多队伍热身赛井字格的模拟都没有过，所以我们放开了时间限制到5s，本来是O(n)的异或正解，但让O(nlogn)的用set、二分之类的的简单模拟也能A掉了。E是一个贪心，最后的结论就是宽取分割后最长的，长也取分割后最长的，相乘即为面积，可以用反证法证明，但是实现还是需要一定的代码能力并且注意一下细节。所以临时修改后第一档的简单题是L、M、J、A、E。预估一下2-3题铜尾。
第二档的中档题我认为是H、B、C、I。H是一个很裸的01背包套了层约束的壳，如果有一定背包基础是可以看出的；B是一个中规中矩的中等的模拟；C是一个贪心，实现也不算太难，细节也是需要注意一下的；I是一个需要细致讨论的毒瘤题，适合和队友疯狂讨论，比较有意思的一道题，赛中想过还是需要队友的默契与比较严谨的逻辑的。银尾4-5题吧应该。
第三档的难题是K、D、G、F。K是以因数10的个数=min(因数5的个数，因数2的个数）为基础所出，利用矩阵快速幂求取所需答案；D是一个利用字符串哈希的可加性，来用线段树优化的题；G本来是一个考GCD性质的题，但是机房众人一直不断加难度，最后成了一个dfs序的线段树维护gcd的题…F是我出的想拿来防AK的计算几何，子弹打靶，想了好久才出的题，本质是先求圆交再求圆并，后来学长zsy居然从一个犄角旮旯找出了求圆并的无敌板子----圆面积并算法，精度极高。我当时想到这题想到的解法是，枚举x轴，求出当前 x = x i x=x_i x=xi与所有小圆的交点，然后扫描线线段求交，同时需要利用子弹所形成圆的半径远小于靶子半径，来二分优化。但是出着出着觉着这题挺好的，不想没人做，就简化了题，把圆面积交去掉了，同时把精度要求降到了绝对误差或相对误差小于0.01即可，想着如果有人感兴趣，乱搞说不定也能过，我也试了两种乱搞，感觉还不错。盲猜金尾5-6题。
A 熊熊占山头
题目描述
在大连海事大学的秘密森林里，有n个山头，现在要将熊熊放回山头，初始时每个山头都没有熊熊。熊熊不允许自己领地里有另一只熊熊，且他们实力相当，如果有两只熊熊在同一个山头，他们会相拼直至双方均死亡。
有q次操作，每次输入一个非负整数x，如果x为0，则表示询问哪个山头有熊熊，输出山头的编号，输入保证目前有且仅有一个山头有熊熊；如果x不为0，则表示将一个熊熊放到山头x。
思路简述
异或性质
正解是O(n)的算法，利用当x=0时有 当且仅当一个山头有熊熊 和 两个熊熊在同一个山头会同时死亡。后一个条件基本直指异或的性质：x^x=0，两个相同的数异或为0，故正解即为简单异或。也可以用bitset优化。
但是因为临时想降低难度，星期六晚上临时把时间限制调到了5s，允许使用set等O(nlogn)简单模拟AC，但需要常数较小。
参考代码1 O(n)
#include 参考代码2 O(nlogn)
#include B 点对点通信
题目描述
Wx是这场比赛命题组的一员，在筹备比赛的过程中，他有很多问题要问xzx，出于试题保密的需求，他俩决定对信息进行二进制编码，采用通信链路进行交流。
现实中的通信链路都不会是理想的，为了保证数据传输的可靠性，在传输数据时，必须采用各种差错检测措施，比如下面所介绍的循环冗余检验CRC。
通过一个例子来说明CRC的原理，对于一个长度为k=6的待传送数据M=101001，CRC运算是在数据M的后面添加供差错检验的n位冗余码，构成一个（k+n）位的数据发送出去。这n位的冗余码计算方式如下。
首先对M乘以 2 n 2^n 2n得到被除数（相当于字符串M后跟n个0），将得到的（k+n）位数进行模2除法（模2除法与算术除法类似，但每一位除的结果不影响其它位，即不向上一位借位，所以实际上就是异或），除以收发双方事先商定的长度为（n+1）的除数P=1101（例中即n=3），得到长度为n的余数R，来作为帧检验序列FCS。最终发送的帧是101001001（即 2 n ∗ M 2^n*M 2n∗M+FCS）。
在接收端对于收到的每一个帧对于相同的P直接进行模2运算（不需要进行乘法运算），当余数R位0时，表示传输过程中无差错。
现用程序模拟上述操作的进行，给定提前约定好的仅有’0’,'1’组成的除数字符串P，给出一个正整数q，表示wx和xzx所不能忍受的传输失败的最小次数。
有如下两种操作，
1)加密：给出字符串M，求M添加FCS后的字符串。
2)解密：给出字符串M，判断M是否存在错误，如果没有错误则输出"No"，如果有错误则输出"Yes"且传输失败的次数加一。
思路简述
模拟
参考代码
#includeC dpj的二分图
题目描述
某人认为其他题的题面华而不实，因此出了一道很严谨的题目。
某人想要构造一个二分图，其满足以下条件：
1. L i 与 右 半 部 分 连 边 会 产 生 费 用 ， 最 后 L i 产 生 的 总 费 用 为 a i D i 1.L_i与右半部分连边会产生费用 ，最后L_i产生的总费用为a_i^{D_i} 1.Li与右半部分连边会产生费用，最后Li产生的总费用为aiDi
2. 若 i 和 j 满 足 1 ≤ j ＜ i ≤ n ， 则 L i 不 能 与 R j 相 连 ; 2. 若 i 和 j 满足 1 ≤ j ＜ i ≤ n ，则L_i不能与 R_j 相连; 2.若i和j满足1≤j＜i≤n，则Li不能与Rj相连;
3. 左 边 部 分 的 点 L i 的 度 D i 满 足 0 ≤ D i ≤ 3 ; 3. 左边部分的点L_i的度D_i 满足0≤ D_i ≤3; 3.左边部分的点Li的度Di满足0≤Di≤3;
4. 右 边 部 分 的 点 R i 的 度 恰 好 等 于 1 ; 4.右边部分的点R_i的度恰好等于1; 4.右边部分的点Ri的度恰好等于1;
对 于 每 个 左 边 部 分 的 的 点 L i ， 有 一 个 对 应 的 a i （ a i 是 已 知 的 ） 。 对于每个左边部分的的点L_i，有一个对应的a_i（a_i是已知的）。 对于每个左边部分的的点Li，有一个对应的ai（ai是已知的）。
L i 与 右 半 部 分 连 边 会 产 生 费 用 ， 最 后 L i 产 生 的 总 费 用 为 a i D i 。 L_i与右半部分连边会产生费用 ，最后L_i产生的总费用为a_i^{D_i}。 Li与右半部分连边会产生费用，最后Li产生的总费用为aiDi。
某 人 想 要 构 造 一 个 满 足 上 述 条 件 的 二 分 图 ， 并 且 使 得 所 有 点 产 生 的 总 费 用 之 和 S = ∑ 1 n a i D i 最 小 , 请 求 出 最 小 的 S 。 某人想要构造一个满足上述条件的二分图，并且使得所有点产生的总费用之和S = \sum_1^n a_i^{D_i}最小, 请求出最小的S 。 某人想要构造一个满足上述条件的二分图，并且使得所有点产生的总费用之和S=∑1naiDi最小,请求出最小的S。
思路简述
贪心+优先队列
从j从1-n，每次贪心的选取和 R j R_j Rj相连所付出的代价最低的 L i L_i Li，而难点就在于需要确定该 L i L_i Li是可以选取(有边)，并且确定所付出代价到底是多少。比如，一个 L i L_i Li点没有边，即度为0，那最后答案即为1，那如果选该点一次，答案应为 a i a_i ai，那么选的代价就应该是 a i − 1 a_i-1 ai−1，同理可得选第二次的代价为 a i 2 − a i a_i^2-a_i ai2−ai，实现需要维护优先队列，并且重载小于号。
参考代码
#include D 连连看与正义熊
题目描述
已入不惑，反青还童的tax又迷上了连连看，醉心于寻找两两相同的快乐，痴迷于不断消去的快感，仿佛昔日狂刷线段树专题一般，勤勤恳恳，夜以继日，夙兴夜寐，沉迷其中。熊熊作为tax成长道路上自封的领路人，十分痛心tax这种醉心于游戏，不知训练的颓废生活，便开始了他的捣蛋之旅。作为计算机大佬的他，掌握了修改tax所玩的那款连连看游戏的能力，每次他可以修改当前连连看上的一个位置上的图标，任意改成他所想的游戏内的图标，从而干扰tax的游戏体验，使他能幡然醒悟，回头是岸，重整旗鼓，继续刷题，重振杰杰所带领的机房的往日光辉。
熊熊想知道他修改的操作影响tax的游戏体验的程度，于是复盘了一次tax的连连看游戏如下，希望你能协助本次复盘。
为简化题意，连连看游戏抽象如下：
将二维的连连看抽象为一个长度为n的由小写字母组成的字符串S。tax和熊熊共有m次操作，熊熊所执行的操作为修改一个位置的字符为任意字符；tax所执行的操作为给出两个相同长度的区间 [ l 1 , r 1 ] [l_1,r_1] [l1,r1] [ l 2 , r 2 ] [l_2,r_2] [l2,r2]，判断字符串S上这两区间的子串是否相同。
思路简述
哈希+线段树
比如对于一个字符串"abcde"，设“abc”的哈希值为123，“de"的哈希值为45,那么”abcde"的哈希值即为 123 ∗ b a s e 2 + 45 123*base^2+45 123∗base2+45，对于这个答案，我们采用线段树来维护，O(mlogn)。
因为线段树进行区间查询的时候，是优先对左子树进行查询的，相当于我们会优先得到字符串前半部分的哈希值，所以对于每次查询到的区间（区间长度为L），我们将我们之前查询得到的哈希值 ∗ b a s e L *base^L ∗baseL即为合并上新区间的哈希值。则询问两个区间的字符串是否相同，只需要求得两个区间的哈希值，比较是否相同。
对于修改字符，我们只需要进行单点修改即可。
参考代码
#include E 矩形分割
题目描述
在一个坐标轴上，有一长为a，宽为b的矩形，其左下角位于坐标轴原点处，矩形的底边长位于x轴上，矩形的左侧宽位于y轴上；在坐标轴上，还有n条垂直于x轴的直线 x = x i x=x_i x=xi，同时有n条垂直于y轴的直线 y = y i y=y_i y=yi，且这些直线均穿过矩形。问原矩形被直线分割后形成的若干矩形中，最大的一块矩形面积是多少。
思路简述
贪心
宽取分割后最长的，长也取分割后最长的，相乘即为面积，可以用反证法证明，此处不作证明。但是实现还是需要一定的代码能力并且注意一下细节，比如需要将两端插入。
参考代码
#include F 熊熊打靶
题目描述
射击场上，海大学子在打靶，小熊看到了这一幕，他盯着靶子，突然对子弹穿过靶子留下的弹洞起了兴趣。
终于轮到小熊射击了，与其他人一样，他也被分配了n发子弹。在一轮的射击完成后，他射光了所有子弹，并取下靶子留做纪念。他很喜欢这个靶子。回到宿舍后，他开始对靶子进行研究，想求出靶子上弹洞的总面积，可他绞尽脑汁也想不出怎么求这么多弹洞所留下的面积，于是求助于参加本次竞赛的你，希望你能解决这个问题。
已知靶子是标准的圆，其半径R=50；子弹穿过靶子所在平面的形状也为标准的圆，其半径为r=0.5；
为简化计算：
1.数据保证子弹不存在擦靶边而过的情况，只有完全命中靶子和未命中靶子两种情况。即：不存在靶子外边缘所成的大圆与子弹外边缘所成的小圆相交的情况。
2.保证子弹垂直射入，即：如命中靶子，靶子所留下的弹洞为半径r=0.5的圆。
3.以靶子的圆心为原点，在靶子所在平面上建立二维坐标系，数据给出n个子弹垂直穿过坐标系平面所成圆的圆心的坐标位置(x_i,y_i)
思路简述
我当时想到这题想到的解法是，枚举x轴，求出当前 x = x i x=x_i x=xi与所有小圆的交点，然后扫描线线段求交，同时需要利用子弹所形成圆的半径远小于靶子半径，来二分优化。但是出着出着觉着这题挺好的，不想没人做，就简化了题，把圆面积交去掉了，同时把精度要求降到了绝对误差或相对误差小于0.01即可，想着如果有人感兴趣，乱搞说不定也能过，我也试了两种乱搞，感觉还不错，但估计没人做。
所以AC的代码将给出两份
一份是计算几何求圆面积并的板子----[圆面积并算法]。
一份是枚举x轴，求出当前 x = x i x=x_i x=xi与所有小圆的交点，然后扫描线线段求交，同时需要利用子弹所形成圆的半径远小于靶子半径，来二分优化。
参考代码1—圆面积并模板
#include参考代码2—枚举+扫描线
#include
//else tmp.push_back(node(x,1.0));
//if(y>high) tmp.push_back(node(high,-1.0));
//else tmp.push_back(node(y,-1.0));
G tax与树上gcd
题目描述
tax最近在玩一款修仙游戏，游戏中他出生于封云宗，在一游历中，他发现了封云宗的宗谱，上面记载着封云宗宗派的传承。
封云宗宗派有n个人，第i个人的代号为i，每个人都有自己的师傅，且封云宗宗派的开山鼻祖代号为1，开山鼻祖没有师傅。
不为人知的是，封云宗宗派修炼了上古的不死功法，每个人仍存活于世，而且每个人都有自己的功力值。
每个封云宗宗派的人面对需要攻击的敌人，可以召唤自己的任意些徒弟和自己联手发动技能，打败敌人的时间是所有召唤的人功力的最大公因数，注意徒弟的徒弟也算作自己的徒弟。
tax偷偷按时间顺序得到q条消息：
第一种消息是知道代号为x的人发动了技能，tax需要求出他击败敌人的最短时间
第二种消息是代号为x的人功力值变成了y
思路简述
dfs序+线段树
对于每一次询问，需要求得以询问点为根的子树上的最小gcd，由贪心的思想可得，我们选取越多的点，gcd的数值会越小，所以对于每次询问，我们选取这颗子树上的全部点，求得所有点权的gcd既为答案。
对于一颗树，我们可以求一遍dfs序，可以将树形数据上的操作映射到对dfs序列的操作。对于dfs序我们需要维护一个区间gcd，可以用线段树来维护区间的gcd的值。
所以对于此题，我们求以1为根的树的dfs序，然后对这个dfs序列用线段树维护区间gcd
参考代码
#includeH 约束条件
思路简述
01背包
01背包套了层约束的壳，定位是道简单的算法题。
参考代码
#include I 01字符串
题目描述
思路简述
博弈论，分类讨论毒瘤题
设一开始全为0或全为1为状态flag=0
若状态不全为0且不全为1为状态flag=1
当n=1时，无论如何都是全为’0’或全为’1’的。
当n=2时，如果flag=0，且有奇数轮，即最后一次是小智选，那么他一定失败，因为对手可以永远保持全为0，全为1，而小智是必须的是非空子序列，故他必须打破这种状态，所以他该情况下他是必输。如果flag=1，且有偶数轮，他也是必输的，因为轮到小智的时候他永远只能调成全为0，全为1的状态，而最后是小智的同学执行操作，是可以打破这种状态的。而n=2的其他情况则小智必胜。
当n=3时，如果flag=0，那么无论k是多少，小智都是必输的，此处可以列举所有情况讨论，在此仅作易错的示例讨论，比如一开始为111，k=3，小智改为010，那么对手可以改为000，小智第三轮无论怎么改都必输；而如果flag=1，则与k有关。
当n>3时，则需要讨论k=1与k的奇偶的情况。
具体请自行理解~
参考代码
#includeJ 最大公因数
题目描述
给定正整数n，判断1~n的全排列中，是否存在任意一种排列p，对于p中每一对相邻的两个数 p i , p i − 1 p_i,p_{i-1} pi,pi−1，满足的对数大于等于 g c d ( p i , p i − 1 ) ≠ 1 gcd(p_i,p_{i-1})\ne1 gcd(pi,pi−1)=1的对数大于等于 ⌊ n 2 ⌋ 表 示 n 2 向 下 取 整 。 \lfloor \frac{n}{2} \rfloor表示\frac{n}{2} 向下取整。 ⌊2n⌋表示2n向下取整。
思路简述
简单构造，如果经常打cf是可以很快看出的。
到了6以后，比如8，都可以按3,6,2,4,8…这样组成<3,6>,<6,2>,<2,4>,<4,8>这样来符合题意
参考代码
#includeK 杰杰的奇妙数列
我是这道题目的出题人dpj，首先在此明确这道题目内容没有问题（题目标题很有问题）。由于这道题代码比较简单，于是我没有验另一个同学写的标程，导致数据出锅。
这道题目需要求0的个数，显然是求式子 f n = t ∗ 1 0 a 中 k f_n = t * 10^a 中k fn=t∗10a中k的数量 ,t 和k是整数，10的质因子只有2 和 5，那么设
g i , 2 为 f i 中 因 子 2 的 个 数 ， g i , 5 为 f i 中 因 子 5 的 个 数 ， 则 a = m i n ( g 2 , i ， g 5 , i ) g_{i,2}为f_i中因子2的个数，g_{i,5}为f_i中因子5的个数，则a=min(g_{2,i}，g_{5,i}) gi,2为fi中因子2的个数，gi,5为fi中因子5的个数，则a=min(g2,i，g5,i).
那么可以分别根据 f 0 和 f 1 求 出 g 0 , 2 ， g 1 , 2 和 g 0 , 5 , g 1 , 5 ， 然 后 讨 论 一 下 g i , 2 和 g i , 5 的 大 小 关 系 ： f_0 和f_1 求出 g_{0,2}，g_{1,2}和g_{0,5},g_{1,5}，然后讨论一下g_{i,2}和g_{i,5}的大小关系： f0和f1求出g0,2，g1,2和g0,5,g1,5，然后讨论一下gi,2和gi,5的大小关系：
显然不论 g 0 和 g 1 g_0和 g_1 g0和g1 的大小关系如何，都会有 g i − 1 < g i ( i > 1 ) g_{i-1}
L 铺地板
题目描述
暄暄的新房子要装修了！可惜暄暄的女朋友是个强迫症，只喜欢正方形的地板。
房子是n*m的矩形，地板的边长是a，最多能放几块完整的地板呢？(不能裁地板）
暄暄是个大佬，根本不屑于解决这种问题，于是他把问题甩给了你~
思路简述
签到，向下取整
参考代码
#includeM Odd vs Even
题目描述
现在有一个问题：给出一个正整数 N，判断它的偶数因子多还是奇数因子多。
写循环从1到N一个一个试，就可以找到正整数N的所有因数，但是要试N次。
最近康康学习了一个新方法，假设a是N的因数，那么N和a的商也是N的因数，所以只要试1到 N \sqrt{N} N就可以找到N的全部因数。
康康想知道更大的数的答案，但很明显新方法也满足不了要求……
思路简述
打表or简单手推
放一个打表的图，还是比较清楚的
打表代码
#include参考代码
#include 总结
由于我们水平确实不够，所以在出题、出数据、写特判上可能有一些不周到的地方，希望大家谅解，希望大家是有一个比较好的参赛体验的，最后希望大家能喜欢上ACM。