利用python手撸一个简单的多层感知机模型
摸鱼时刻。基本的深度学习原理,很早就接触了,前向传播、反向传播等都有了解,但是一直没自己实现过,虽然说站在巨人的肩膀上可以看的更远,但理解底层会让你站的更稳。
神经网络反向传播算法利用链式求导法则进行,链式求导计算图在程序实现过程中需要使用拓扑排序。
今天用python实现一个简单的y=wx+b模型,也算是对秋季学期《神经网络原理》课程的总结。
import numpy as np
import random
class Node:
def __init__(self, inputs=[]):
self.inputs = inputs
self.outputs = []
for n in self.inputs:
n.outputs.append(self)
self.value = None
self.gradients = {
}
def forward(self):
"""
前向计算过程
对输入节点的计算结果保存在self.value
"""
raise NotImplemented
def backward(self):
raise NotImplemented
class Placeholder(Node):
def __init__(self):
"""
输入节点没有入站节点,所以无需在node实例化传递任何参数
"""
Node.__init__(self)
def forward(self, value=None):
"""
除了输入节点,其他节点的实现都应获得上一个节点的值
如:val0: self.inbound_nodes[0].value
"""
if value is not None:
self.value = value
def backward(self):
self.gradients = {
self : 0}
for n in self.outputs:
grad_cost = n.gradients[self]
self.gradients[self] = grad_cost * 1
# class Add(Node):
# def __init__(self, *nodes):
# Node.__init__(self, nodes)
# def forward(self):
# self.value = sum(map(lambda n : n.value, self.inputs))
# ## 当forward执行时,会按照定义计算值
class Linear(Node):
def __init__(self, nodes, weights, bias):
Node.__init__(self, [nodes, weights, bias])
def forward(self):
inputs = self.inputs[0].value
weights = self.inputs[1].value
bias = self.inputs[2].value
self.value = np.dot(inputs, weights) + bias
def backward(self):
# 给每个入站节点初始化一个偏导
self.gradients = {
n : np.zeros_like(n.value) for n in self.inputs}
for n in self.outputs:
grad_cost = n.gradients[self]
self.gradients[self.inputs[0]] = np.dot(grad_cost, self.inputs[1].value.T)
self.gradients[self.inputs[1]] = np.dot(self.inputs[0].value.T, grad_cost)
self.gradients[self.inputs[2]] = np.sum(grad_cost, axis=0, keepdims=False)
class Sigmoid(Node):
def __init__(self, node):
Node.__init__(self, [node])
def _sigmoid(self, x):
return 1./(1+np.exp(-1*x))
def forward(self):
self.x = self.inputs[0].value
self.value = self._sigmoid(self.x)
def backward(self):
# y = 1 / (1 + e^-x)
# y' = 1 / (1 + e^-x) (1 - 1 / (1 + e^-x))
self.partial = self._sigmoid(self.x) * (1-self._sigmoid(self.x))
self.gradients = {
n : np.zeros_like(n.value) for n in self.inputs}
for n in self.outputs:
grad_cost = n.gradients[self]
self.gradients[self.inputs[0]] = grad_cost * self.partial
class MSE(Node):
def __init__(self, y, a):
Node.__init__(self, [y, a])
def forward(self):
y = self.inputs[0].value.reshape(-1, 1)
a = self.inputs[1].value.reshape(-1, 1)
assert y.shape == a.shape, 'y.shape is not a.shape'
self.m = self.inputs[0].value.shape[0]
self.diff = y - a
self.value = np.mean(self.diff**2)
def backward(self):
self.gradients[self.inputs[0]] = (2 / self.m) * self.diff
self.gradients[self.inputs[1]] = (-2 / self.m) * self.diff
def forward_backward(graph):
# 执行已排序节点的前向传播
for n in graph:
n.forward()
# 执行已排序节点的后向传播
for n in graph[::-1]:
n.backward()
def toplogic(graph):
"""
拓扑排序
"""
sorted_node = []
while len(graph) > 0:
all_inputs = []
all_outputs = []
for n in graph:
all_inputs += graph[n]
all_outputs.append(n)
all_inputs = set(all_inputs)
all_outputs = set(all_outputs)
need_remove = all_outputs - all_inputs
if len(need_remove) > 0:
node = random.choice(list(need_remove))
need_to_visited = [node]
if len(graph) == 1:
need_to_visited += graph[node]
graph.pop(node)
sorted_node += need_to_visited
for _, links in graph.items():
if node in links:
links.remove(node)
else:
break
return sorted_node
from collections import defaultdict
def convert_feed_dict_to_graph(feed_dict):
computing_graph = defaultdict(list)
nodes = [n for n in feed_dict]
while nodes:
n = nodes.pop(0)
if isinstance(n, Placeholder):
n.value = feed_dict[n]
if n in computing_graph:
continue
for m in n.outputs:
computing_graph[n].append(m)
nodes.append(m)
return computing_graph
def topological_sort_feed_dict(feed_dict):
graph = convert_feed_dict_to_graph(feed_dict)
return toplogic(graph)
def optimize(trainables, learning_rate=1e-2):
# 有很多其他的优化方法,这里只实现一个简单的例子
for t in trainables:
t.value += -1 * learning_rate * t.gradients[t]
import numpy as np
from sklearn.datasets import load_boston
from sklearn.utils import shuffle, resample
# 加载数据
data = load_boston()
X_ = data['data']
y_ = data['target']
# 归一化
X_ = (X_ - np.mean(X_, axis=0)) / np.std(X_, axis=0)
n_features = X_.shape[1]
n_hidden = 10
W1_ = np.random.randn(n_features, n_hidden)
b1_ = np.zeros(n_hidden)
W2_ = np.random.randn(n_hidden, 1)
b2_ = np.zeros(1)
# 网络
X, y = Placeholder(), Placeholder()
W1, b1 = Placeholder(), Placeholder()
W2, b2 = Placeholder(), Placeholder()
l1 = Linear(X, W1, b1)
s1 = Sigmoid(l1)
l2 = Linear(s1, W2, b2)
cost = MSE(y, l2)
feed_dict = {
X: X_,
y: y_,
W1: W1_,
b1: b1_,
W2: W2_,
b2: b2_
}
epochs = 2000
m = X_.shape[0]
batch_size = 16
steps_per_epoch = m // batch_size
graph = topological_sort_feed_dict(feed_dict)
trainables = [W1, b1, W2, b2]
print("Total number of examples = {}".format(m))
Total number of examples = 506
losses = []
for i in range(epochs):
loss = 0
for j in range(steps_per_epoch):
# step1: 加载数据
X_batch, y_batch = resample(X_, y_, n_samples=batch_size)
X.value = X_batch
y.value = y_batch
# step 2
forward_backward(graph)
rate = 1e-2
optimize(trainables, rate)
loss += graph[-1].value
losses.append(loss/steps_per_epoch)
if i % 100 == 0:
print('epoch: {}, loss: {:.3f}'.format(i+1, loss/steps_per_epoch))
epoch: 1, loss: 156.041
epoch: 101, loss: 7.104
epoch: 201, loss: 5.069
epoch: 301, loss: 4.563
epoch: 401, loss: 4.201
epoch: 501, loss: 3.764
epoch: 601, loss: 3.474
epoch: 701, loss: 3.783
epoch: 801, loss: 3.587
epoch: 901, loss: 3.141
epoch: 1001, loss: 3.449
epoch: 1101, loss: 4.105
epoch: 1201, loss: 3.464
epoch: 1301, loss: 2.986
epoch: 1401, loss: 3.237
epoch: 1501, loss: 2.817
epoch: 1601, loss: 3.482
epoch: 1701, loss: 3.022
epoch: 1801, loss: 3.317
epoch: 1901, loss: 3.016
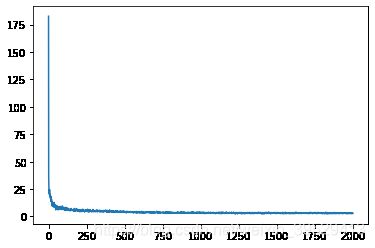
plt.plot(losses)