集成学习案例——工业蒸汽预测

origin from: datawhale
reference: https://blog.csdn.net/weixin_42565558/article/details/104570584

学习背景简介

背景介绍

火力发电的基本原理是：燃料在燃烧时加热水生成蒸汽，蒸汽压力推动汽轮机旋转，然后汽轮机带动发电机旋转，产生电能。在这一系列的能量转化中，影响发电效率的核心是锅炉的燃烧效率，即燃料燃烧加热水产生高温高压蒸汽。锅炉的燃烧效率的影响因素很多，包括锅炉的可调参数，如燃烧给量，一二次风，引风，返料风，给水水量；以及锅炉的工况，比如锅炉床温、床压，炉膛温度、压力，过热器的温度等。我们如何使用以上的信息，根据锅炉的工况，预测产生的蒸汽量，来为我国的工业届的产量预测贡献自己的一份力量呢？

所以，该案例是使用以上工业指标的特征，进行蒸汽量的预测问题。由于信息安全等原因，我们使用的是经脱敏后的锅炉传感器采集的数据（采集频率是分钟级别）。

数据信息

数据分成训练数据（train.txt）和测试数据（test.txt），其中字段”V0”-“V37”，这38个字段是作为特征变量，”target”作为目标变量。我们需要利用训练数据训练出模型，预测测试数据的目标变量。

评价指标

最终的评价指标为均方误差MSE，即：
$$Score=\frac{1}{n}\sum _1^n(y_i-y^{\ast }{)}^2$$

数据观测与初步处理

import warnings
warnings.filterwarnings("ignore")
import matplotlib.pyplot as plt
import seaborn as sns

# 模型
import pandas as pd
import numpy as np
from scipy import stats
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV, RepeatedKFold, cross_val_score,cross_val_predict,KFold
from sklearn.metrics import make_scorer,mean_squared_error,r2_score
from sklearn.linear_model import LinearRegression, Lasso, Ridge, ElasticNet
from sklearn.svm import LinearSVR, SVR
from sklearn.neighbors import KNeighborsRegressor
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor,AdaBoostRegressor
from xgboost import XGBRegressor
from sklearn.preprocessing import PolynomialFeatures,MinMaxScaler,StandardScaler

#37维变量，最后一列为target

data_train=pd.read_csv('train.txt',sep='\t')
data_test=pd.read_csv('test.txt',sep='\t')
data_all=pd.concat([data_train,data_test],axis=0,ignore_index=True)

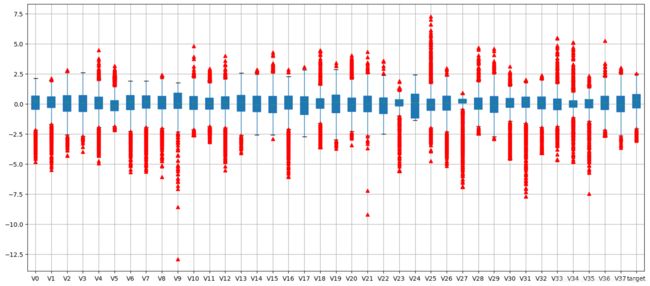
#观察数据基本分布情况

plt.figure(figsize=(18,8),dpi=100)
data_all.boxplot(sym='r^',patch_artist=True,notch=True)

def heatmap(df):
    plt.figure(figsize=(20,16),dpi=100)# 指定绘图对象宽度和高度以及分辨率
    cols=df.columns.tolist() #列表头
    mcorr=df[cols].corr(method='spearman') #相关系数矩阵，任意两个变量之间的相关
    cmap=sns.diverging_palette(220,10,as_cmap=True)  
    mask=np.zeros_like(mcorr,dtype=np.bool)# 构造与mcorr同维数矩阵 为bool型
    mask[np.triu_indices_from(mask)] = True              # 角分线右侧为True
    g = sns.heatmap(mcorr, mask=mask, cmap=cmap, square=True, annot=True, fmt='0.2f')
    plt.xticks(rotation=45)
    return mcorr
    
data_train_mcorr = heatmap(data_train)

数据具体处理

#降维操作，将相关性的绝对值小于阈值的特征进行删除

threshold=0.1
corr_matrix=data_train.corr().abs()
drop_col=corr_matrix[corr_matrix['target']<threshold].index
data_all.drop(drop_col,axis=1,inplace=True)

#降维操作，将相关性的绝对值小于阈值的特征进行删除

threshold=0.1
corr_matrix=data_train.corr().abs()
drop_col=corr_matrix[corr_matrix['target']<threshold].index
data_all.drop(drop_col,axis=1,inplace=True)

#归一化

cols_numeric=list(data_all.columns)
def scale_minmax(col):
    return (col-col.min())/(col.max()-col.min())
scale_cols = [col for col in cols_numeric if col!='target']
data_all[scale_cols] = data_all[scale_cols].apply(scale_minmax,axis=0)
data_all[scale_cols].describe()

进一步观测与特征工程

#连续变量，使用核密度估计图初步分析即EDA1。EDA价值主要在于熟悉了解整个数据集的基本情况（缺失值，异常值），
#对数据集进行验证是否可以进行接下来的机器学习或者深度学习建模.了解变量间的相互关系、变量与预测值之间的存在关系。为特征工程做准备

for column in data_all.columns[0:-2]:
    #核密度估计(kernel density estimation)是在概率论中用来估计未知的密度函数，属于非参数检验方法之一。通过核密度估计图可以比较直观的看出数据样本本身的分布特征。
    g = sns.kdeplot(data_train[column], color="Red", shade = True)
    g = sns.kdeplot(data_test[column], ax =g, color="Blue", shade= True)
    g.set_xlabel(column)
    g.set_ylabel("Frequency")
    g = g.legend(["train","test"])
    plt.show()

#删除训练集数据分布于测试集数据分布差异过大的特征数据

data_all.drop(["V5","V9","V11","V17","V22","V28"],axis=1,inplace=True)

#查看各特征与结果变量的相关性，以及是否服从正态分布

plt.figure(figsize=(20,70),dpi=80)
i = 0
for col in data_train.columns:
    i += 1
    plt.subplot(20,4,i)
    sns.regplot(col, 'target', data = data_train,
               scatter_kws = {
     'marker': '.', 's': 5, 'alpha': .6},
               line_kws = {
     'color': 'k'})
    coef = np.corrcoef(data_train[col], data_train['target'])[0][1]
    plt.title(f'coef = {coef}')
    plt.xlabel(col)
    plt.ylabel('target')
    
    i += 1
    plt.subplot(20,4,i)
    sns.distplot(data_train[col], fit = stats.norm)
    plt.title(f'skew = {stats.skew(data_train[col])}')
    plt.xlabel(col)
    
plt.tight_layout()

#相关性低的此前已处理，现对偏态数据进行正态化转换

# 分布呈明显左偏的特征
piantai = ['V0','V1','V6','V7','V8','V12','V16','V31']

# 创建函数——找到令偏态系数绝对值最小的对数转换的底
def find_min_skew(data):
    subs = list(np.arange(1.01,2,0.01))
    skews = []
    for x in subs:
        skew = abs(stats.skew(np.power(x,data)))
        skews.append(skew)
    min_skew = min(skews)
    i = skews.index(min_skew)
    return subs[i], min_skew

def split_data_all():
    data_train=data_all[data_all['target'].notnull()]
    data_test=data_all[data_all['target'].isnull()]
    data_test.drop('target',axis=1,inplace=True)
    return data_train,data_test

for col in piantai:
    sub=find_min_skew(data_all[col])[0]
    data_all[col]=np.power(sub,data_all[col])

data_train,data_test=split_data_all()

#对剩余特征采取z-score标准化

data_all.iloc[:,:-1]=data_all.iloc[:,:-1].apply(lambda x:(x-x.mean())/x.std())

data_train,data_test=split_data_all()

plt.figure(figsize=(20,20),dpi=80)
for i in range(22):
    plt.subplot(6,4,i+1)
    sns.distplot(data_train.iloc[:,i], color='green')
    sns.distplot(data_test.iloc[:,i], color='red')
    plt.legend(['Train','Test'])
plt.tight_layout()

#将训练数据分为训练集和验证集
import numpy as np
X=np.array(data_train.iloc[:,:-1])
y=np.array(data_train['target'])

X_train,X_valid,y_train,y_valid=train_test_split(X,y,test_size=0.2,random_state=0)

#创建模型评分函数

def score(y,y_pred):
	# 计算均方误差 MSE
    print('MSE = {0}'.format(mean_squared_error(y, y_pred)))
    # 计算模型决定系数 R2
    print('R2 = {0}'.format(r2_score(y, y_pred)))

          
    #找异常点
    y = pd.Series(y)
    y_pred = pd.Series(y_pred,index=y.index)
    
    resid=y-y_pred
    mean_resid=resid.mean()
    std_resid=resid.std()
    z=(resid-mean_resid)/std_resid
    n_outliers=sum(abs(z)>3)
    
          
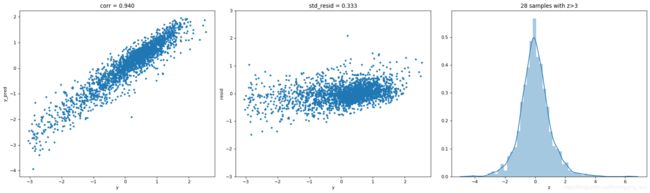
    #真实值vs预计值
    plt.figure(figsize=(20,6),dpi=80)
    plt.subplot(131)
    plt.plot(y,y_pred,'.')
    plt.xlabel('y')
    plt.ylabel('y_pred')
    plt.title('corr = {:.3f}'.format(np.corrcoef(y,y_pred)[0][1]))
    
    #残差分布散点图
    plt.subplot(132)
    plt.plot(y,y-y_pred,'.')
    plt.xlabel('y')
    plt.ylabel('resid')
    plt.ylim([-3,3])
    plt.title('std_resid = {:.3f}'.format(std_resid))
          
    #残差z得分直方图
    plt.subplot(133)
    sns.distplot(z, bins=50)
    plt.xlabel('z')
    plt.title('{:.0f} samples with z>3'.format(n_outliers))
    plt.tight_layout()

# 利用RidgeCV函数自动寻找最优参数

from sklearn.linear_model import LinearRegression, RidgeCV, LassoCV
ridge = RidgeCV()
ridge.fit(X_train, y_train)
print('best_alpha = {0}'.format(ridge.alpha_))

y_pred = ridge.predict(X_train)
score(y_train, y_pred)

best_alpha = 0.1
MSE = 0.11102493447366545
R2 = 0.8831339524176028

#找出异常样本点并删除

resid = y_train - y_pred
resid = pd.Series(resid, index=range(len(y_train)))
resid_z = (resid-resid.mean()) / resid.std()
outliers = resid_z[abs(resid_z)>3].index
print(f'{len(outliers)} Outliers:')
print(outliers.tolist())

plt.figure(figsize=(14,6),dpi=60)

plt.subplot(121)
plt.plot(y_train, y_pred, '.')
plt.plot(y_train[outliers], y_pred[outliers], 'ro')
plt.title(f'MSE = {mean_squared_error(y_train,y_pred)}')
plt.legend(['Accepted', 'Outliers'])
plt.xlabel('y_train')
plt.ylabel('y_pred')

plt.subplot(122)
sns.distplot(resid_z, bins = 50)
sns.distplot(resid_z.loc[outliers], bins = 50, color = 'r')
plt.legend(['Accepted', 'Outliers'])
plt.xlabel('z')
plt.tight_layout()

28 Outliers:
[89, 407, 692, 768, 797, 829, 907, 1123, 1190, 1236, 1295, 1324, 1366, 1458, 1544, 1641, 1706, 1718, 1796, 1833, 1983, 2013, 2022, 2124, 2152, 2227, 2279, 2299]

#删除异常样本点

X_train = np.array(pd.DataFrame(X_train).drop(outliers,axis=0))
y_train = np.array(pd.Series(y_train).drop(outliers,axis=0))

模型训练

#进行模型的训练

def get_training_data_omitoutliers():
    y=y_train.copy()
    X=X_train.copy()
    return X,y

def train_model(model, param_grid=[],X=[],y=[],splits=5, repeats=5):

    #获取数据
    if len(y)==0:
        X,y=get_training_data_omitoutliers()
    #交叉验证
    rkfold=RepeatedKFold(n_splits=splits,n_repeats=repeats)
    
    #网格搜索最佳参数
    if len(param_grid)>0:
        gsearch = GridSearchCV(model, param_grid, cv=rkfold,
                               scoring="neg_mean_squared_error",
                               verbose=1, return_train_score=True)

        # 训练
        gsearch.fit(X,y)

        # 最好的模型
        model = gsearch.best_estimator_        
        best_idx = gsearch.best_index_

        # 获取交叉验证评价指标
        grid_results = pd.DataFrame(gsearch.cv_results_)
        cv_mean = abs(grid_results.loc[best_idx,'mean_test_score'])
        cv_std = grid_results.loc[best_idx,'std_test_score']

    # 没有网格搜索  
    else:
        grid_results = []
        cv_results = cross_val_score(model, X, y, scoring="neg_mean_squared_error", cv=rkfold)
        cv_mean = abs(np.mean(cv_results))
        cv_std = np.std(cv_results)
    
    # 合并数据
    cv_score = pd.Series({
     'mean':cv_mean,'std':cv_std})

    # 预测
    y_pred = model.predict(X)
    
    # 模型性能的统计数据        
    print('----------------------')
    print(model)
    print('----------------------')
    print('score=',model.score(X,y))
    print('rmse=',rmse(y, y_pred))
    print('mse=',mse(y, y_pred))
    print('cross_val: mean=',cv_mean,', std=',cv_std)
    
    # 残差分析与可视化
    y = pd.Series(y)
    y_pred = pd.Series(y_pred,index=y.index)
    resid = y - y_pred
    mean_resid = resid.mean()
    std_resid = resid.std()
    z = (resid - mean_resid)/std_resid    
    n_outliers = sum(abs(z)>3)
    outliers = z[abs(z)>3].index
    
    return model, cv_score, grid_results

def rmse(y_true, y_pred):
    diff = y_pred - y_true
    sum_sq = sum(diff**2)    
    n = len(y_pred)   
    return np.sqrt(sum_sq/n)

def mse(y_ture,y_pred):
    return mean_squared_error(y_ture,y_pred)

# scorer to be used in sklearn model fitting
rmse_scorer = make_scorer(rmse, greater_is_better=False) 

#输入的score_func为记分函数时，该值为True（默认值）；输入函数为损失函数时，该值为False
mse_scorer = make_scorer(mse, greater_is_better=False)

#定义训练变量存储数据

opt_models=dict()
score_models=pd.DataFrame(columns=['mean','std'])
splits=5
repeats=5

model='Ridge'
opt_models[model]=Ridge()
alph_range = np.arange(0.25,6,0.25)
param_grid = {
     'alpha': alph_range}

opt_models[model],cv_score,grid_results = train_model(opt_models[model], param_grid=param_grid,splits=splits, repeats=repeats)
cv_score.name=model
score_models=score_models.append(cv_score)

plt.figure()
plt.errorbar(alph_range, abs(grid_results['mean_test_score']),
             abs(grid_results['std_test_score'])/np.sqrt(splits*repeats))
plt.xlabel('alpha')
plt.ylabel('score')

Fitting 25 folds for each of 23 candidates, totalling 575 fits
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
----------------------
Ridge(alpha=0.25, copy_X=True, fit_intercept=True, max_iter=None,
      normalize=False, random_state=None, solver='auto', tol=0.001)
----------------------
score= 0.8995591410381618
rmse= 0.3052491903405309
mse= 0.09317706820354954
cross_val: mean= 0.09600844824389711 , std= 0.008127104484170745
[Parallel(n_jobs=1)]: Done 575 out of 575 | elapsed:    0.9s finished
Text(0, 0.5, 'score')