永磁同步电机的直接转矩控制（一）一一一DTC仿真模型的搭建

永磁同步电机的直接转矩控制（一）一一一DTC仿真模型的搭建

0研究背景

---

写在前面：
 1.本代码基于MATLAB2019a版本，低版本或者不同版本可能会报错，mdl文件或slx文件打开可能会失败；
 2.本博客附上仿真模型并详细介绍各个部分的搭建，如果转载请注明出处；
 3.如果本博客恰巧与您的研究有所关联，欢迎您的咨询qq1366196286。

---

1直接转矩控制的简单介绍

本博客介绍了永磁同步电机直接转矩控制系统中各个环节的MATLAB/Simulink建模方法，并对系统进行仿真研究了系统的性能以及PI控制器参数对系统性能的影响，同时比较了不同转矩滞环环宽的转矩脉动情形。

该DTC仿真模型可作为后续改进的基础。结果表明，该系统具有良好的转速、转矩响应。

随着转矩滞环环宽的变小，转矩的脉动幅度也随之减小。PI控制器参数中，随着比例系数Kp的增大，系统动态响应加快，积分系数Ki则主要影响系统的稳态误差，两者必须协调才能使系统达到较好的性能。

---

  基础的概念及介绍请参考文献：
[1] 袁雷,胡冰新,魏克银,等.现代永磁同步电机控制原理及MATLAB仿真[M].北京:北京航空航天大学出版社,2016(03):12-18.
[2] 谢运祥,卢柱强.基于MATLAB/Simulink的永磁同步电机直接转矩控制仿真建模[J].华南理工大学学报（自然科学版）
,2004,32(1):19-23.
[3] 马晓哲. 基于dSPACE的PMSM无速度传感器直接转矩控制研究[D]. 天津:天津理工大学,2018. DOI:10.7666/d.D01415320.
[4] 何萍,郭军. 基于Matlab/Simulink的异步电机直接转矩控制系统仿真[J]. 电气应用,2007,26(1):84-87. DOI:10.3969/j.issn.1672-9560.2007.01.023.

---

   永磁同步电机因结构简单、转矩电流比高、功率密度大等优点在动力驱动领域应用广泛。尽管传统的双闭环矢量 PI 控制系统具有调速范围宽、响应速度快、加减速性能好等优点，但它存在着算法的实现须经过复杂的坐标变换，转子位置高度依赖电机参数而难以精准定向，电机运行时内部参数动态耦合强等缺点。为此，1985 年，德国 M.Depenbrock 教授第一次提出六边形直接转矩控制策略，并应用在感应电机调速系统中。1986 年，日本高桥熏教授提出了另外一种圆形直接转矩控制策略。

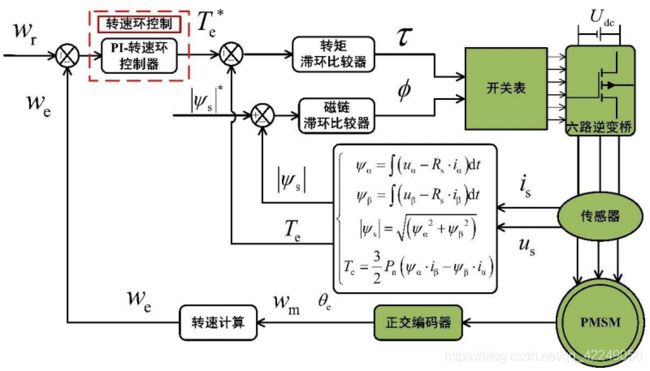
直接转矩控制是利用Bang-Bang控制（滞环控制）产生PWM信号，对逆变器的开关状态进行最佳控制，从而获得转矩的高动态性能。其基本操作是：将磁链转矩设定值与磁链转矩实际值的误差传给滞环比较器，并经过离线运算开关表获得合适的电机空间矢量，从而实现电机的调速控制，如图 1 所示。

   与基于转子磁场定向控制的矢量控制相比，基于定子磁场定向控制的直接转矩控制拥有以下优点：
   1.省去了矢量控制等复杂的变换计算，系统直观、简洁，计算速度和精度都比矢量控制方式有所提高；
   2.控制结构简单。DTC仅需要两个滞环控制器和一个转速环PI调节器；
   3.控制器的计算均在定子上的静止坐标系中进行，避免了复杂的旋转坐标变换复杂计算，大大地简化了运算处理过程，提高了控制运算速度。同时也避免了磁链定向控制受转子参数的影响。
   4.其中所使用的两个滞环控制器直接控制定子磁链和转矩，而不是像矢量控制那样，通过控制定子电流的两个分量间接地控制电机的磁链和转矩，它追求转矩控制的快速性和准确性。不需要过分的追求圆形磁链轨迹和正弦波电流。
   5.根据磁链和转矩的滞环控制器输出，直接对逆变器功率器件的导通与关断进行最佳控制，最终产生离散的PWM电压输出。其中比矢量控制少了PWM控制环节。

   总结：直接转矩控制具有鲁棒性强、转矩动态响应速度快、控制结构简单等优点。

其中：矢量控制的详细介绍可参考博主的博客：
永磁同步电机的矢量控制策略系列讲解
永磁同步电机的矢量控制策略（八）一一一仿真模型搭建与源代码

   但直接转矩控制也存在着一些缺点，主要是低速时转矩脉动大：
   1.但由于它借助滞环比较器产生 PWM 控制波，使得逆变器的开关频率抖动大，转矩脉动也比较大。
   2.当电机低速运行时，定子电阻压降大且磁链计算误差大，从而使得 DTC 调速范围窄。
   3.由于转矩和磁链调节器采用滞环比较器，不可避免地造加粗样式成了转矩脉动;
   4.在电动机运行一段时间之后,电机的温度升高,定子电阻的阻值发生变化,使定子磁链的估计精度降低，导致电磁转矩出现较大的脉动;若仅考虑温升影响定子电阻会出现 25%~40%的变化。
   5.逆变器开关频率的高低也会影响转矩脉动的大小，开关频率越高转矩脉动越小，反之开关频率越低转矩脉动越大。

图1 永磁同步电机的直接转矩控制框图

---

图2 永磁同步电机的直接转矩控制Simulink仿真图

---

2控制系统仿真模型的搭建

2.1 被控对象的数学模型及控制框图

  借助于之前在定子坐标系上所建立的PMSM数学模型，进行直接转矩控制的数学模型搭建。其中，数学模型可参考博主之前的博客：永磁同步电机的矢量控制策略（二）一一一数学模型

图2 两相旋转d-q坐标系与两相静止α-β坐标系之间的关系

图1 永磁同步电机的直接转矩控制框图

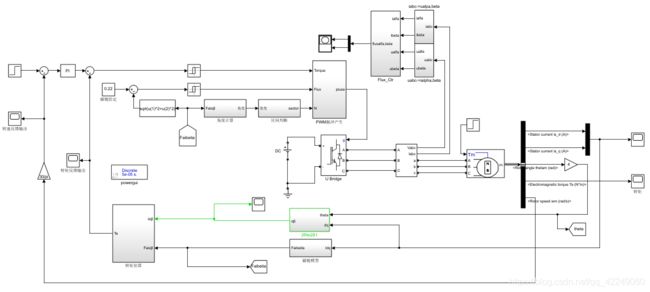
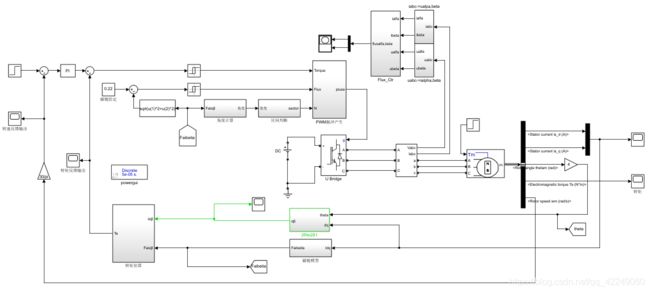
  如图1所示，直接转矩控制是由逆变器、SPMSM、磁链估算、转矩估算、转子位置估算、开关表和调节器等部分组成。其中，控制系统将电机给定转速和实际转速的误差，经转速环调节器输出为给定转矩信号；同时，控制系统根据所检测的电机三相电流和电压值，利用磁链估算模型和转矩估算模型分别计算电机参考的磁链和转矩大小，进而计算电机转子的位置、电机给定磁链和转矩与实际值的误差；然后根据它们的状态选择逆变器的开关矢量，使电机能够按控制要求调节输出转矩，最终达到调速的目的。

2.2 磁链的估算模型及仿真图

图3 磁链估算模型的仿真Simulink图

图4 a-β轴上的合成圆形磁链

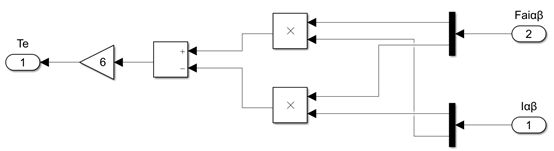
2.3 转矩的估算模型及仿真图

图5 转矩估算的仿真模型

图6 a-β轴上磁链的仿真图

图7 转矩估算的仿真图

转子位置Theta是依据α-β坐标系上的转子磁链投影进行计算的，如下图所示。

图8 转子位置Theta的仿真模型

图9 转子位置Theta的仿真图

2.4 扇区判断及开关表

图10 电压矢量和扇区划分

磁链区间段与角度之间的关系

图11 扇区划分的Simulink仿真图

图12 扇区划分的仿真结果

2.5 PWM的生成

图13 电压矢量增量图

图14 PWM生成的仿真图

图15 PWM生成的仿真结果图

---

3仿真结果及分析

（1）转速响应

转速为阶跃转速，0.5s由800 r/min阶跃上升至1000 r/min

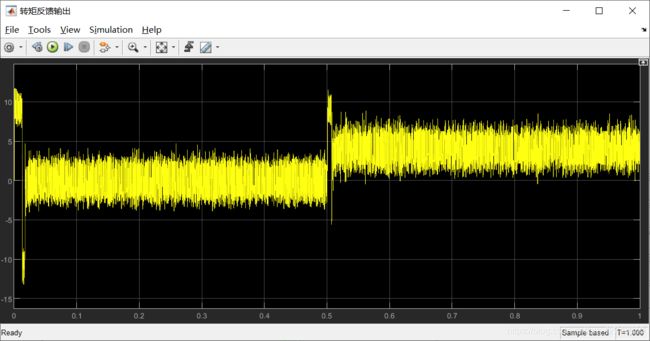
（2）转矩响应

转矩为阶跃转矩，0s由0 N·m阶跃上升至4 N·m

（3）a-β轴的电流响应

---

4总结

1.转速超调现象严重，转速波动性较大；
2.相电流谐波成分大，转矩脉动较大。
为此，后续将基于以此为demo模型对直接转矩控制进行改进设计，并更新该系列的博客。敬请期待，感谢大家的关注与支持！！！

参考文献

[1] 袁雷,胡冰新,魏克银,等.现代永磁同步电机控制原理及MATLAB仿真[M].北京:北京航空航天大学出版社,2016(03):12-18. [2] 谢运祥,卢柱强.基于MATLAB/Simulink的永磁同步电机直接转矩控制仿真建模[J].华南理工大学学报（自然科学版） ,2004,32(1):19-23. [3] 马晓哲. 基于dSPACE的PMSM无速度传感器直接转矩控制研究[D]. 天津:天津理工大学,2018. DOI:10.7666/d.D01415320. [4] 何萍,郭军. 基于Matlab/Simulink的异步电机直接转矩控制系统仿真[J]. 电气应用,2007,26(1):84-87. DOI:10.3969/j.issn.1672-9560.2007.01.023.