Mixer阅读笔记
Mixer阅读笔记
Tolstikhin I, Houlsby N, Kolesnikov A, et al. MLP-Mixer: An all-MLP Architecture for Vision[J]. arXiv preprint arXiv:2105.01601, 2021.
很久没有看论文了,前一段时间又在准备考试……其实就是懒了点哈哈哈,五一回来在arxiv上看到这篇paper,看了abstract觉得这篇paper有点意思,点进pdf一看各种画风,遥想vision transformer当年,盲审露头了,雄姿英发,文中的行文逻辑和flowchart都让我在恍惚中想起了今天随处可见的跨界transformer,那恰到好处的圆角,那似曾相似的配色,那听起来就很大但是我就是不公开的JFT,那属于上流高端玩家的TPU,我就问,还有谁!就决定是你了,Google Research!不过这次人家也不盲审,反正就是玩,我甚至都没看到作者我都可以猜到都是那些老姐,强是强,全是高端玩家的操作。当时就码住了,准备等到机器学习考试完了再看,谁知等了两天,关注的公众号基本上到处都是这篇文章,都是什么杀疯了!又有坑了!这些标题我上一次看到还是对vision transfromer说的。
算了,进入正题吧!
感知机和一段历史
这里我又要BB一下,由于刚进行了机器学习考试,打算趁刚预习的机器学习的知识还没有全部忘完,我打算看看Bishop的PRML,顺便开个机器学习板块,希望在毕业之前能够更几篇哈哈哈(坑是要挖,但是要量力挖,免得把自己活埋在里面了)。
讲MLP之前我想要先讲一段历史,关于现代深度神经网络的。1956年的达特茅斯会议上,Artificial Intelligence这个名词正式确定,也正式确定了AI的任务,这次会议被广泛认为是AI诞生的标志,那时的AI和2014年的人工智能领域很像,那时的计算机AI有一种神奇的魔力,大量的研究者都很乐观,很多人都相信真正智能时代不久将会到来,那个不久只需20年。那时的ARPA(现在叫做DARPA,我老师的口头禅)眼里,这就是未来,投了大量的资金到这个新兴领域,一定要最先占领这个新战场!
达特茅斯会议一年后也就是1957年,Rosenblatt根据生物神经网络的特点提出了一个带有两层神经元的神经网络——感知机(Perceptron),这是世界上首个可以学习的结构,在当时引发了巨大的轰动,可以说我上面说的那种研究者当时对于AI那种近乎宗教式的狂热有很大程度就因为这个感知机,人们兴奋的以为自己发现了智能的秘密。说到这,你可能回想这玩意儿有这么神奇?我们来看看结构:
感知机包括两个部分,输入如上图中的 x 1 , x 2 , x 3 x_1, x_2, x_3 x1,x2,x3,只负责将输入递交给输出模块; w 1 , w 2 , w 3 w_1, w_2, w_3 w1,w2,w3代表权重;而 Z Z Z代表输出,也是计算的核心模块。直观上,我们在做决策的时候,是把考虑多个因素,然后由于多个因素在你心中的重要性不同,所以有个权重,最后你综合这些权重和因素得出一个决策是或否。正如上面的 x 1 , x 2 , x 3 x_1, x_2, x_3 x1,x2,x3就是各个被量化的考虑因素, w 1 , w 2 , w 3 w_1, w_2, w_3 w1,w2,w3代表权重, Z Z Z代表决策结果-1/+1,而 Z = s g n ( x 1 × w 1 + x 2 × w 2 + x 3 × w 3 ) Z=sgn(x_1\times w_1 + x_2 \times w_2 + x_3 \times w_3) Z=sgn(x1×w1+x2×w2+x3×w3),当然也可以写成矩阵形式 Z = s g n ( W T X ) \textbf{Z}=sgn(W^TX) Z=sgn(WTX)。人类不是在一次次学习对各个事件分配不同权重吗,感知机也一样,学习的是权重分配,直观上这就是仿生学嘛,仿人类智能。
从几何上理解, W T X + b = 0 W^TX+b=0 WTX+b=0就是特征空间中的一个超平面(1957的感知机没有添加bias,现在主流应用的时候都加了bias同时为了方便讲解,所以加了个bias),其中 W W W是超平面的法向量, b b b是超平面的截距。这个超平面将特征空间分为了两个部分。位于两部分的点(即特征向量)分别被分为正、负两类,所以这是个线性二分类有监督算法,所以这个超平面也被称之为分离超平面(separating hyperplane)。为什么会叫做超平面:对n维线性可分数据,需要n-1维平面来进行分割,比如二维数据只需要一条线,三维只需要一个面,那么四维五维甚至更高维呢?所以我们统一称为超平面。
感知机想要做到给定一个数据集,如果存在某个超平面S( W T X + b = 0 W^TX+b=0 WTX+b=0),能够将数据集的正例和负例完全正确的划分到超平面的两侧,即对y=+1的实例点,有 W T X + b > 0 W^TX+b>0 WTX+b>0,对y=-1的实例点,有 W T X + b < 0 W^TX+b<0 WTX+b<0,则称数据集线性可分,否则线性不可分。要找这个能够完全正确分类的平面就是感知机的权重学习过程。那具体怎么学习权重的呢?从几何的角度,如上图,要用一条直线来对红蓝两个类别做分类,就是要让错误分类的点越少越好,但是如果我们选择点的个数作为度量,是离散的自然数,不可导,所以我们选择误分类点到分类超平面的距离作为标准,点到平面的距离: ∣ w x + b ∣ ∣ ∣ w ∣ ∣ \frac{|wx+b|}{||w||} ∣∣w∣∣∣wx+b∣,什么是误分类点呢?根据前面的表述就是 y i ( w x + b ) < 0 y_i(wx+b)<0 yi(wx+b)<0的点,所以误分类总距离即为 1 ∣ ∣ w ∣ ∣ ∑ x i ∈ M y i ( w x + b ) < 0 \frac{1}{||w||}\sum\limits_{x_i\in M} y_i(wx+b)<0 ∣∣w∣∣1xi∈M∑yi(wx+b)<0,然后转化为一个最小化问题便于优化 − 1 ∣ ∣ w ∣ ∣ ∑ x i ∈ M y i ( w x + b ) -\frac{1}{||w||}\sum\limits_{x_i\in M} y_i(wx+b) −∣∣w∣∣1xi∈M∑yi(wx+b),即要最小化这个方程, 1 ∣ ∣ w ∣ ∣ \frac{1}{||w||} ∣∣w∣∣1不考虑(为什么不考虑参见传送门),那么优化问题变为 L ( w , b ) = − ∑ x i ∈ M y i ( w x + b ) \mathcal{L}(w,b)=-\sum\limits_{x_i\in M} y_i(wx+b) L(w,b)=−xi∈M∑yi(wx+b)。
但是正如我上面所说,感知机是一个线性二分类有监督算法,它不能表达复杂的函数,不能出来线性不可分的问题,其连异或问题(XOR,如下图,只切一刀明显无法分开这两类数据)都无法解决。可惜啊,那时候的人们被这种莫名的喜悦冲昏了头脑,直到1969年Minsky出版了《Perceptron》一书,提出了感知机对异或问题的难题,这一盆带有Minsky声望光环的冷水基本上直接浇灭了大片的星星之火,这一事件标志着AI的第一次寒冬,当时教父级人物Minsky的极度悲观直接导致了长达十年的“AI winter”,对联结主义的研究带来了巨大的打击,很多实验室直接放弃对神经网络的研究。由于AI的进展缓慢,DARPA和NRC对无方向的AI研究逐渐停止了资助。其实不止Minsky,早在1966年ALPAC的报告中就有批评机器翻译进展的意味,预示了这一局面的来临。NRC,1973年詹姆斯·莱特希尔针对英国AI研究状况的报告批评了AI在实现其“宏伟目标”上的完全失败,并导致了英国AI研究的低潮在拨款二千万美元后停止资助。2016年Minsky在美国去世。
MLP
Minsky提出单层感知机不能解决异或问题,但是当增加一个计算层以后,两层神经网络不仅可以解决异或问题,而且具有非常好的非线性分类效果。其实当时Minsky并不是没有想到将单个感知机进行拼接,但是Minsky指出,多层感知机的结构导致其计算成为一个难以解决的问题。将单层感知机进行拼接,得到的多层感知机(MLP)如下:
其实这里计算和单层感知机差不多,先对中间紫色节点按照单层感知机进行计算,然后将紫色节点当成输入节点再对绿色节点进行计算即可。这里其实已经很像人工神经网络(ANN)了,但是这里还没有back propagation,直到《Perceptron》30年后,Hinton和Rumelhart提出back propagation,人工智能才焕发第二春。
文章主要思想
虽然……但是……,今天的深度神经网络的成功必须要感谢当年那些在寒冬里不懈努力的人,不幸的是Rosenblatt不能再看到今天的局面了,他在《感知器》问世后不久即因游船事故去世。而Google Research今天的这篇文章,当时看到的时候我感觉MLP又要行了哈哈哈。
这篇文章提出了一个叫做Mixer的模型,这个model完全是没有使用CNN结果,主要的结构就是MLP,它包含一个能够融合token的MLP层和一个融合空间信息的MLP层,两个MLP层相互独立,并先后对图像patch进行特征提取,然后将其送入一个全局池化和全连接层,就这么简单。
Details
整个处理流程图如上图所示,你感受这个图和vision transformer那个。。。。其实我觉得我下图的浪漫手绘更好懂一点,如果不嫌弃的话可以瞅瞅。首先将图片划分为patch,每个patch为 P × P P \times P P×P,那么就有 H × W P \frac{H\times W}{P} PH×W个patch,然后将每个patch直接展开成一个向量,对每个patch进行FC操作,将其映射到 R C \mathbb{R}^C RC空间,将每个patch的向量进行拼接成一个二维张量,张量的每一行看成一个token(patch),每一个token的每一维看成一个channel。然后将张量进行转置后输入一个隐层为 R D S \mathbb{R}^{D_S} RDS的二维多层感知机里,这个多层感知机是对行操作(列间参数共享),转置后的行就是token,所以这个就是文中所说的token-mix MLP,通过这个多层感知机后张量大小不变,再将其进行一次转置,转置后再次输入一个隐层为 R D C \mathbb{R}^{D_C} RDC感知机中,再次对行进行操作,这次的行代表每一个channel,所以是文中的channel mix MLP,将输出结果放入一个全局池化和分类器输出结果。以下是我的浪漫手绘:
两个感知机的公式表示如下,作者利用了skip connection和layer norm,同时这里的非线性函数采用的GLEU:
U ∗ , i = X ∗ , i + W 2 σ ( W 1 LayerNorm ( X ) ∗ , i ) , for i = 1 … C , Y j , ∗ = U j , ∗ + W 4 σ ( W 3 LayerNorm ( U ) j , ∗ ) , for j = 1 … S . \begin{array}{ll} \mathbf{U}_{*, i} & =\mathbf{X}_{*, i}+\mathbf{W}_{2} \sigma\left(\mathbf{W}_{1} \text { LayerNorm }(\mathbf{X})_{*, i}\right), & \text { for } i=1 \ldots C, \\ \mathbf{Y}_{j, *} & =\mathbf{U}_{j, *}+\mathbf{W}_{4} \sigma\left(\mathbf{W}_{3} \text { LayerNorm }(\mathbf{U})_{j, *}\right), & \text { for } j=1 \ldots S . \end{array} U∗,iYj,∗=X∗,i+W2σ(W1 LayerNorm (X)∗,i),=Uj,∗+W4σ(W3 LayerNorm (U)j,∗), for i=1…C, for j=1…S.
实验
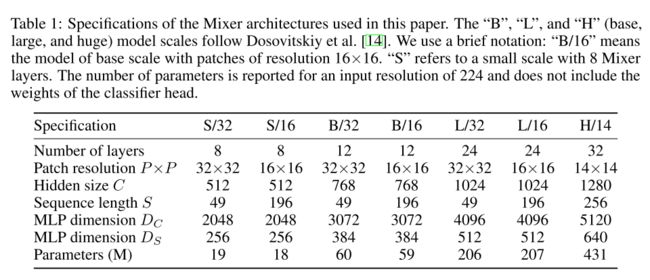
延续这批人一贯的特点,实验做得非常漂亮,而且我就在大量的数据集上,我就在JFT上,怎么办你用不着,你比不了,你有TPU吗?以下是实验的超参,操就连不同size模型的命名都不变一下。
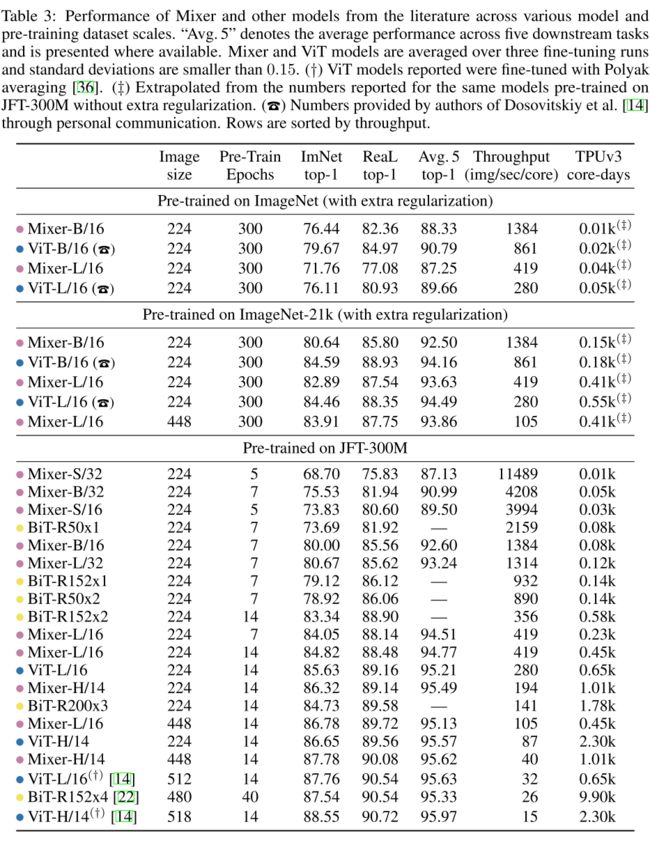
结果也贴出来大家高兴高兴,文中还有很多实验细节,大家有兴趣可以移步原文:
一些想法
- 我感觉Google Research好喜欢把图像划分为patch来处理,其实我一直比较怀疑这种处理方式对于图像信息的损失,越是多的patch,我觉得损失越严重,transformer里面有些工作为了防止这种情况是为patch加了identity,但是这里貌似没加。
- 和喷子LeCun不一样,我也不太同意他把这种Mixer看成是大kernel卷积和1$\times$1卷积的结合,但是Mixer并没有达到SOTA,正如文章中说的。
- 最近的transformer和Mixer到底是在证明一个什么呢?CNN不是特征提取的必要模块?获取是吧,但是尽管很多Google吹们说的天花乱坠,说实话,我不知道layer norm,skip connection对mixer到底有多重要。
- 这批文章附录还提了一个section讨论一些不太起作用的操作,比如不sharing MLP列间参数等等,这个很有意思,这种权值共享CNN里也有。
但是这篇文章对于我来说还是提供了一些很好的insight,希望不会和transformer那样的水论文工具。