图文详解WGAN及其变体WGAN-GP并利用Tensorflow2实现WGAN与WGAN-GP
图文详解WGAN及其变体WGAN-GP并利用Tensorflow2实现WGAN与WGAN-GP
- 构建WGAN(Wasserstein GAN)
-
- Wasserstein loss介绍
- 1-Lipschitz约束的实现
- 训练过程
- 实现梯度惩罚(WGAN-GP)
- 完整代码
构建WGAN(Wasserstein GAN)
自GAN提出以来,许多论文尝试通过使用启发式方法(例如尝试不同的网络体系结构,超参数和优化器)来解决GAN训练的不稳定性。随着Wasserstein GAN(WGAN)的提出,这一问题的研究得到了重大突破。
WGAN缓解甚至消除了许多GAN训练过程中存在的问题。相较于原始GAN的其根本的改进是对损失函数的修改。从理论上讲,如果两个分布不相交,则JS散度将不再是连续的,因此将不可微,从而导致梯度为零。 WGAN通过使用一个新的损失函数来解决此问题,该函数在任何地方都是连续且可微的!
Wasserstein loss介绍
对于原始GAN的目标函数,我们都已经耳熟能详,在此简单进行回顾:
m i n G m a x D V ( D , G ) = E x ∼ p t a t a ( x ) [ l o g D ( x ) ] + E z ∼ p z ( z ) [ l o g ( 1 − D ( G ( z ) ) ) ] min_Gmax_DV(D,G)=E_{x\sim p_{tata}(x)}[logD(x)] +E_{z\sim p_z(z)}[log(1-D(G(z)))] minGmaxDV(D,G)=Ex∼ptata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))]
其中, D D D表示鉴别器, G G G表示生成器, x x x表示真实数据, z z z表示潜在变量。
将上述形式进行转换,可以得到如下值函数形式:
E x ∼ p t a t a ( x ) [ l o g D ( x ) ] + E z ∼ p z ( z ) [ l o g D ( G ( z ) ) ] E_{x\sim p_{tata}(x)}[logD(x)] +E_{z\sim p_z(z)}[logD(G(z))] Ex∼ptata(x)[logD(x)]+Ez∼pz(z)[logD(G(z))]
WGAN使用一种新的损失函数,称为推土机距离或Wasserstein距离。它用于度量将一种分布转换为另一种分布所需的距离或工作量。从数学上讲,这是真实图像与生成图像之间每个联合分布的最小距离,WGAN的值函数变为:
E x ∼ p d a t a ( x ) [ D ( x ) ] − E z ∼ p z ( z ) [ D ( G ( z ) ) ] E_{x\sim p_{data}(x)}[D(x)]-E_{z\sim p_z(z)}[D(G(z))] Ex∼pdata(x)[D(x)]−Ez∼pz(z)[D(G(z))]
我们将使用此函数推导得到损失函数,首先第一项可以写为:
− 1 N ∑ i = 1 N y i D ( x ) -\frac1N\sum_{i=1}^Ny_iD(x) −N1i=1∑NyiD(x)
这是鉴别器输出的平均值乘以-1。我们通过使用 y i y_i yi作为标签,其中+1代表真实图像,而-1代表虚假图像。因此,我们可以将Wasserstein损失实现为TensorFlow Keras自定义损失函数,如下所示:
def wasserstein_loss(self, y_true, y_pred):
w_loss = -tf.reduce_mean(y_true*y_pred)
return w_loss
它旨在使真实图像相对于伪图像的得分最大化。因此,在WGAN中,鉴别器也被称为评论家(critic)。
但是由于WGAN删除了鉴别器的输出中sigmoid激活函数。因此,评论家的预测是无限的,需要通1-Lipschitz进行约束。
1-Lipschitz约束的实现
Wasserstein损失中提到的数学假设是1-Lipschitz函数。我们说评论家D(x)如果满足以下不等式,则为1-Lipschitz:
∣ D ( x 1 ) − D ( x 2 ) ∣ ≤ ∣ x 1 − x 2 ∣ |D(x_1)-D(x_2)|\leq|x_1-x_2| ∣D(x1)−D(x2)∣≤∣x1−x2∣
对于两个图像 x 1 x_1 x1和 x 2 x_2 x2,评论家的输出差异的绝对值必须小于或等于其平均逐像素差的绝对值。换句话说,对于不同的图像,无论是真实图像还是伪造图像,评论家的输出不应有太大差异。当WGAN提出时,作者无法想到适当的实施方式来实现此不等式。因此,他们想出了一个办法,就是将评论家的权重降低到一些很小的值。这样,层的输出以及最终评论家的输出都被限制在一些较小的值上。在WGAN论文中,权重被限制在[-0.01,0.01]的范围内。
权重裁剪可以通过两种方式实现。一种方法是编写一个自定义约束函数,并在实例化新层时使用它,如下所示:
class WeightsClip(tf.keras.constraints.Constraint):
def __init__(self, min_value=-0.01, max_value=0.01):
self.min_value = min_value
self.max_value = max_value
def __call__(self, w):
return tf.clip_by_value(w, self.min, self.max_value)
然后,可以将函数传递给接受约束函数的层,如下所示:
model = tf.keras.Sequential(name='critics')
model.add(Conv2D(16, 3, strides=2, padding='same',
kernel_constraint=WeightsClip(),
bias_constraint=WeightsClip()))
model.add(BatchNormalization(
beta_constraint=WeightsClip(),
gamma_constraint=WeightsClip()))
但是,在每个层创建过程中添加约束代码会使代码变得臃肿。由于我们不需要挑选要裁剪的层,因此可以使用循环读取权重,裁剪后将其写回,如下所示:
对于comment.layers中的层:
for layer in critic.layers:
weights = layer.get_weights()
weights = [tf.clip_by_value(w, -0.01, 0.01) for w in weights]
layer.set_weights(weights)
训练过程
在原始GAN理论中,应该在生成器之前对鉴别器进行训练。但在实践中,由于鉴别器能更快的训练,因此鉴别器的梯度将逐渐消失。有了Wasserstein损失函数后,可以在任何地方推导梯度,将不必担心评论家相较生成器过于强大。
因此,在WGAN中,对于生成器的每一个训练步骤,评论家都会接受五次训练。为了做到这一点,我们将评论家训练步骤写为一个单独的函数,然后可以循环多次:
for _ in range(self.n_critic):
real_images = next(data_generator)
critic_loss = self.train_critic(real_images, batch_size)
生成器的训练步骤:
self.critic = self.build_critic()
self.critic.trainable = False
self.generator = self.build_generator()
critic_output = self.critic(self.generator.output)
self.model = Model(self.generator.input, critic_output)
self.model.compile(loss = self.wasserstein_loss, optimizer = RMSprop(3e-4))
self.critic.trainable = True
在前面的代码中,通过设置trainable = False冻结了评论者层,并将其链接到生成器以创建一个新模型并进行编译。之后,我们可以将评论家设置为可训练,这不会影响我们已经编译的模型。
我们使用train_on_batch()API执行单个训练步骤,该步骤将自动进行前向计算,损失计算,反向传播和权重更新:
g_loss = self.model.train_on_batch(g_input, real_labels)
尽管较原始GAN方面有所改进,但训练WGAN十分困难,并且所产生的图像质量并不比原始GAN更好。接下来,将实现WGAN的变体WGAN-GP,该变体训练速度更快,并产生更清晰的图像。
实现梯度惩罚(WGAN-GP)
正如WGAN作者所承认的那样,权重裁剪并不是实施Lipschitz约束的理想方法。其有两个缺点:网络容量使用不足和梯度爆炸/消失。当我们裁剪权重时,我们也限制了评论家的学习能力。权重裁剪迫使网络仅学习简单特征。因此,神经网络的容量变得未被充分利用。其次,裁剪值需要仔细调整。如果设置得太高,梯度会爆炸,从而违反了Lipschitz约束。如果设置得太低,则随着网络反向传播,梯度将消失。同样,权重裁剪会将梯度推到两个极限值,如下图所示: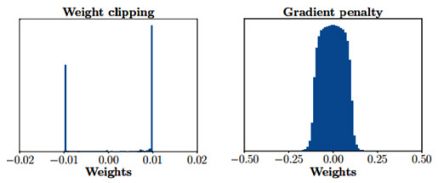
因此,提出了梯度惩罚(GP)来代替权重裁剪以强制实施Lipschitz约束,如下所示:
G r a d i e n t p e n a l t y = λ E x ^ [ ( ∥ ∇ x ^ D ( x ^ ) ∥ 2 − 1 ) 2 ] Gradient\ penalty = \lambda E\hat x[(\lVert \nabla _{\hat x}D(\hat x) \rVert_2-1)^2] Gradient penalty=λEx^[(∥∇x^D(x^)∥2−1)2]
我们将查看方程式中的每个变量,并在代码中实现它们。
我们通常使用 x x x表示真实图像,但是现在方程式中有一个 x ^ \hat x x^。 x ^ \hat x x^是真实图像和伪图像之间的逐点插值。从[0,1]的均匀分布中得出图像比率(epsilon):
epsilon = tf.random.uniform((batch_size,1,1,1))
interpolates = epsilon*real_images + (1-epsilon)*fake_images
根据WGAN-GP论文,就我们的目的而言,我们可以这样理解,因为梯度来自真实图像和伪造图像的混合,因此我们不需要分别计算真实和伪造图像的损失。
∇ x ^ D ( x ^ ) \nabla _{\hat x}D(\hat x) ∇x^D(x^)项是评论家输出相对于插值的梯度。我们可以再次使用tf.GradientTape()来获取梯度:
with tf.GradientTape() as gradient_tape:
gradient_tape.watch(interpolates)
critic_interpolates = self.critic(interpolates)
gradient_d = gradient_tape.gradient(critic_interpolates, [interpolates])
下一步是计算L2范数:
∥ ∇ x ^ D ( x ^ ) ∥ 2 \lVert \nabla _{\hat x}D(\hat x) \rVert_2 ∥∇x^D(x^)∥2
我们对每个值求平方,将它们加在一起,然后求平方根:
grad_loss = tf.square(grad)
grad_loss = tf.reduce_sum(grad_loss, axis=np.arange(1, len(grad_loss.shape)))
grad_loss = tf.sqrt(grad_loss)
在执行tf.reduce_sum()时,我们排除了轴上的第一维,因为该维是batch大小。惩罚旨在使梯度范数接近1,这是计算梯度损失的最后一步:
grad_loss = tf.reduce_mean(tf.square(grad_loss - 1))
等式中的 λ λ λ是梯度惩罚与其他评论家损失的比率,在本这里中设置为10。现在,我们将所有评论家损失和梯度惩罚添加到反向传播并更新权重:
total_loss = loss_real + loss_fake + LAMBDA * grad_loss
gradients = total_tape.gradient(total_loss, self.critic.variables)
self.optimizer_critic.apply_gradients(zip(gradients, self.critic.variables))
这就是需要添加到WGAN中以使其成为WGAN-GP的所有内容。不过,需要删除以下部分:
- 权重裁剪
- 评论家中的批标准化
梯度惩罚是针对每个输入独立地对评论者的梯度范数进行惩罚。但是,批规范化会随着批处理统计信息更改梯度。为避免此问题,批规范化从评论家中删除。
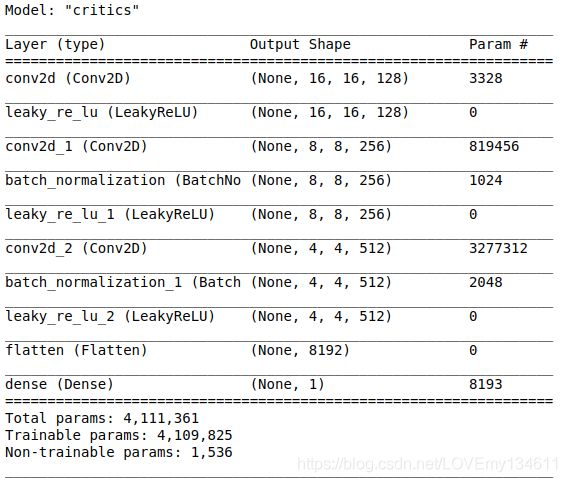
评论家体系结构与WGAN相同,但不包括批规范化:
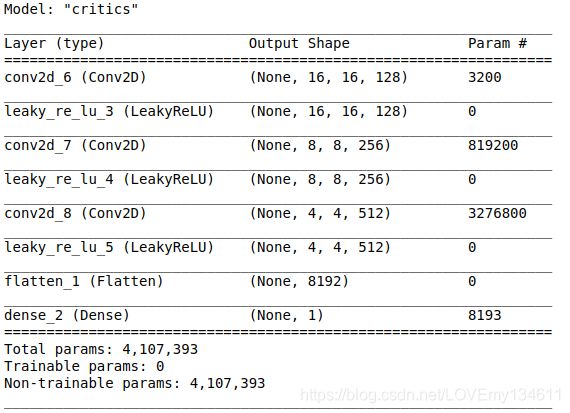
它们看起来清晰漂亮,非常类似于Fashion-MNIST数据集中的样本。训练非常稳定,很快就收敛了!
完整代码
# wgan_and_wgan_gp.py
import tensorflow as tf
from tensorflow.keras import layers, Model
from tensorflow.keras.activations import relu
from tensorflow.keras.models import Sequential, load_model
from tensorflow.keras.callbacks import ModelCheckpoint, EarlyStopping
from tensorflow.keras.losses import BinaryCrossentropy
from tensorflow.keras.optimizers import RMSprop, Adam
from tensorflow.keras.metrics import binary_accuracy
import tensorflow_datasets as tfds
import numpy as np
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
print("Tensorflow", tf.__version__)
ds_train, ds_info = tfds.load('fashion_mnist', split='train',shuffle_files=True,with_info=True)
fig = tfds.show_examples(ds_train, ds_info)
batch_size = 64
image_shape = (32, 32, 1)
def preprocess(features):
image = tf.image.resize(features['image'], image_shape[:2])
image = tf.cast(image, tf.float32)
image = (image-127.5)/127.5
return image
ds_train = ds_train.map(preprocess)
ds_train = ds_train.shuffle(ds_info.splits['train'].num_examples)
ds_train = ds_train.batch(batch_size, drop_remainder=True).repeat()
train_num = ds_info.splits['train'].num_examples
train_steps_per_epoch = round(train_num/batch_size)
print(train_steps_per_epoch)
"""
WGAN
"""
class WGAN():
def __init__(self, input_shape):
self.z_dim = 128
self.input_shape = input_shape
# losses
self.loss_critic_real = {
}
self.loss_critic_fake = {
}
self.loss_critic = {
}
self.loss_generator = {
}
# critic
self.n_critic = 5
self.critic = self.build_critic()
self.critic.trainable = False
self.optimizer_critic = RMSprop(5e-5)
# build generator pipeline with frozen critic
self.generator = self.build_generator()
critic_output = self.critic(self.generator.output)
self.model = Model(self.generator.input, critic_output)
self.model.compile(loss = self.wasserstein_loss,
optimizer = RMSprop(5e-5))
self.critic.trainable = True
def wasserstein_loss(self, y_true, y_pred):
w_loss = -tf.reduce_mean(y_true*y_pred)
return w_loss
def build_generator(self):
DIM = 128
model = tf.keras.Sequential(name='Generator')
model.add(layers.Input(shape=[self.z_dim]))
model.add(layers.Dense(4*4*4*DIM))
model.add(layers.BatchNormalization())
model.add(layers.ReLU())
model.add(layers.Reshape((4,4,4*DIM)))
model.add(layers.UpSampling2D((2,2), interpolation="bilinear"))
model.add(layers.Conv2D(2*DIM, 5, padding='same'))
model.add(layers.BatchNormalization())
model.add(layers.ReLU())
model.add(layers.UpSampling2D((2,2), interpolation="bilinear"))
model.add(layers.Conv2D(DIM, 5, padding='same'))
model.add(layers.BatchNormalization())
model.add(layers.ReLU())
model.add(layers.UpSampling2D((2,2), interpolation="bilinear"))
model.add(layers.Conv2D(image_shape[-1], 5, padding='same', activation='tanh'))
return model
def build_critic(self):
DIM = 128
model = tf.keras.Sequential(name='critics')
model.add(layers.Input(shape=self.input_shape))
model.add(layers.Conv2D(1*DIM, 5, strides=2, padding='same'))
model.add(layers.LeakyReLU(0.2))
model.add(layers.Conv2D(2*DIM, 5, strides=2, padding='same'))
model.add(layers.BatchNormalization())
model.add(layers.LeakyReLU(0.2))
model.add(layers.Conv2D(4*DIM, 5, strides=2, padding='same'))
model.add(layers.BatchNormalization())
model.add(layers.LeakyReLU(0.2))
model.add(layers.Flatten())
model.add(layers.Dense(1))
return model
def train_critic(self, real_images, batch_size):
real_labels = tf.ones(batch_size)
fake_labels = -tf.ones(batch_size)
g_input = tf.random.normal((batch_size, self.z_dim))
fake_images = self.generator.predict(g_input)
with tf.GradientTape() as total_tape:
# forward pass
pred_fake = self.critic(fake_images)
pred_real = self.critic(real_images)
# calculate losses
loss_fake = self.wasserstein_loss(fake_labels, pred_fake)
loss_real = self.wasserstein_loss(real_labels, pred_real)
# total loss
total_loss = loss_fake + loss_real
# apply gradients
gradients = total_tape.gradient(total_loss, self.critic.trainable_variables)
self.optimizer_critic.apply_gradients(zip(gradients, self.critic.trainable_variables))
for layer in self.critic.layers:
weights = layer.get_weights()
weights = [tf.clip_by_value(w, -0.01, 0.01) for w in weights]
layer.set_weights(weights)
return loss_fake, loss_real
def train(self, data_generator, batch_size, steps, interval=200):
val_g_input = tf.random.normal((batch_size, self.z_dim))
real_labels = tf.ones(batch_size)
for i in range(steps):
for _ in range(self.n_critic):
real_images = next(data_generator)
loss_fake, loss_real = self.train_critic(real_images, batch_size)
critic_loss = loss_fake + loss_real
# train generator
g_input = tf.random.normal((batch_size, self.z_dim))
g_loss = self.model.train_on_batch(g_input, real_labels)
self.loss_critic_real[i] = loss_real.numpy()
self.loss_critic_fake[i] = loss_fake.numpy()
self.loss_critic[i] = critic_loss.numpy()
self.loss_generator[i] = g_loss
if i%interval == 0:
msg = "Step {}: g_loss {:.4f} critic_loss {:.4f} critic fake {:.4f} critic_real {:.4f}"\
.format(i, g_loss, critic_loss, loss_fake, loss_real)
print(msg)
fake_images = self.generator.predict(val_g_input)
self.plot_images(fake_images)
self.plot_losses()
def plot_images(self, images):
grid_row = 1
grid_col = 8
f, axarr = plt.subplots(grid_row, grid_col, figsize=(grid_col*2.5, grid_row*2.5))
for row in range(grid_row):
for col in range(grid_col):
if self.input_shape[-1]==1:
axarr[col].imshow(images[col,:,:,0]*0.5+0.5, cmap='gray')
else:
axarr[col].imshow(images[col]*0.5+0.5)
axarr[col].axis('off')
plt.show()
def plot_losses(self):
fig, (ax1, ax2) = plt.subplots(2, sharex=True)
fig.set_figwidth(10)
fig.set_figheight(6)
ax1.plot(list(self.loss_critic.values()), label='Critic loss', alpha=0.7)
ax1.set_title("Critic loss")
ax2.plot(list(self.loss_generator.values()), label='Generator loss', alpha=0.7)
ax2.set_title("Generator loss")
plt.xlabel('Steps')
plt.show()
wgan = WGAN(image_shape)
wgan.generator.summary()
wgan.critic.summary()
wgan.train(iter(ds_train), batch_size, 2000, 100)
z = tf.random.normal((8, 128))
generated_images = wgan.generator.predict(z)
wgan.plot_images(generated_images)
wgan.generator.save_weights('./wgan_models/wgan_fashion_minist.weights')
"""
WGAN_GP
"""
class WGAN_GP():
def __init__(self, input_shape):
self.z_dim = 128
self.input_shape = input_shape
# critic
self.n_critic = 5
self.penalty_const = 10
self.critic = self.build_critic()
self.critic.trainable = False
self.optimizer_critic = Adam(1e-4, 0.5, 0.9)
# build generator pipeline with frozen critic
self.generator = self.build_generator()
critic_output = self.critic(self.generator.output)
self.model = Model(self.generator.input, critic_output)
self.model.compile(loss=self.wasserstein_loss, optimizer=Adam(1e-4, 0.5, 0.9))
def wasserstein_loss(self, y_true, y_pred):
w_loss = -tf.reduce_mean(y_true*y_pred)
return w_loss
def build_generator(self):
DIM = 128
model = Sequential([
layers.Input(shape=[self.z_dim]),
layers.Dense(4*4*4*DIM),
layers.BatchNormalization(),
layers.ReLU(),
layers.Reshape((4,4,4*DIM)),
layers.UpSampling2D((2,2), interpolation='bilinear'),
layers.Conv2D(2*DIM, 5, padding='same'),
layers.BatchNormalization(),
layers.ReLU(),
layers.UpSampling2D((2,2), interpolation='bilinear'),
layers.Conv2D(2*DIM, 5, padding='same'),
layers.BatchNormalization(),
layers.ReLU(),
layers.UpSampling2D((2,2), interpolation='bilinear'),
layers.Conv2D(image_shape[-1], 5, padding='same', activation='tanh')
],name='Generator')
return model
def build_critic(self):
DIM = 128
model = Sequential([
layers.Input(shape=self.input_shape),
layers.Conv2D(1*DIM, 5, strides=2, padding='same', use_bias=False),
layers.LeakyReLU(0.2),
layers.Conv2D(2*DIM, 5, strides=2, padding='same', use_bias=False),
layers.LeakyReLU(0.2),
layers.Conv2D(4*DIM, 5, strides=2, padding='same', use_bias=False),
layers.LeakyReLU(0.2),
layers.Flatten(),
layers.Dense(1)
], name='critics')
return model
def gradient_loss(self, grad):
loss = tf.square(grad)
loss = tf.reduce_sum(loss, axis=np.arange(1, len(loss.shape)))
loss = tf.sqrt(loss)
loss = tf.reduce_mean(tf.square(loss - 1))
loss = self.penalty_const * loss
return loss
def train_critic(self, real_images, batch_size):
real_labels = tf.ones(batch_size)
fake_labels = -tf.ones(batch_size)
g_input = tf.random.normal((batch_size, self.z_dim))
fake_images = self.generator.predict(g_input)
with tf.GradientTape() as gradient_tape, tf.GradientTape() as total_tape:
# forward pass
pred_fake = self.critic(fake_images)
pred_real = self.critic(real_images)
# calculate losses
loss_fake = self.wasserstein_loss(fake_labels, pred_fake)
loss_real = self.wasserstein_loss(real_labels, pred_real)
# gradient penalty
epsilon = tf.random.uniform((batch_size, 1, 1, 1))
interpolates = epsilon * real_images + (1-epsilon) * fake_images
gradient_tape.watch(interpolates)
critic_interpolates = self.critic(interpolates)
gradients_interpolates = gradient_tape.gradient(critic_interpolates, [interpolates])
gradient_penalty = self.gradient_loss(gradients_interpolates)
# total loss
total_loss = loss_fake + loss_real + gradient_penalty
# apply gradients
gradients = total_tape.gradient(total_loss, self.critic.variables)
self.optimizer_critic.apply_gradients(zip(gradients, self.critic.variables))
return loss_fake, loss_real, gradient_penalty
def train(self, data_generator, batch_size, steps, interval=100):
val_g_input = tf.random.normal((batch_size, self.z_dim))
real_labels = tf.ones(batch_size)
for i in range(steps):
for _ in range(self.n_critic):
real_images = next(data_generator)
loss_fake, loss_real, gradient_penalty = self.train_critic(real_images, batch_size)
critic_loss = loss_fake + loss_real + gradient_penalty
# train generator
g_input = tf.random.normal((batch_size, self.z_dim))
g_loss = self.model.train_on_batch(g_input, real_labels)
if i%interval == 0:
msg = "Step {}: g_loss {:.4f} critic_loss {:.4f} critic fake {:.4f} critic_real {:.4f} penalty {:.4f}".format(i, g_loss, critic_loss, loss_fake, loss_real, gradient_penalty)
print(msg)
fake_images = self.generator.predict(val_g_input)
self.plot_images(fake_images)
def plot_images(self, images):
grid_row = 1
grid_col = 8
f, axarr = plt.subplots(grid_row, grid_col, figsize=(grid_col*2.5, grid_row*2.5))
for row in range(grid_row):
for col in range(grid_col):
if self.input_shape[-1]==1:
axarr[col].imshow(images[col,:,:,0]*0.5+0.5, cmap='gray')
else:
axarr[col].imshow(images[col]*0.5+0.5)
axarr[col].axis('off')
plt.show()
wgan = WGAN_GP(image_shape)
wgan.train(iter(ds_train), batch_size, 5000, 100)
wgan.model.summary()
wgan.critic.summary()
z = tf.random.normal((8, 128))
generated_images = wgan.generator.predict(z)
wgan.plot_images(generated_images)