BFS算法和DFS算法（含图解：简单易懂）
图解BFS算法和DFS算法
- BFS算法
-
- 算法思路
- 实现过程
- Python代码实现
- DFS算法
-
- 算法思路
- 实现过程
- Python代码实现
BFS算法
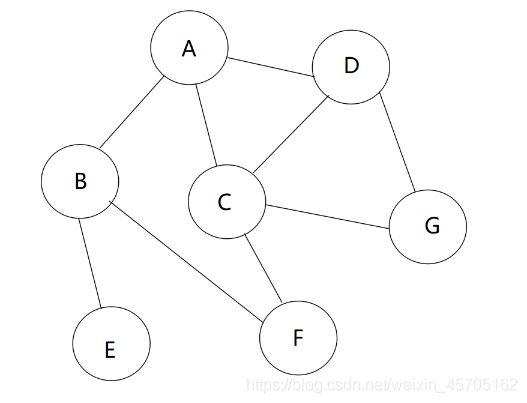
BFS类似于树的层次遍历过程,从根节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。
舍去空间换时间。
算法思路
队列（先进先出）
1、创建一个空队列queue（用来存放节点）和一个空列表visit（用来存放已访问的节点）
2、依次将起始点及邻接点加入queue和visit中
3、poo出队列中最先进入的节点,从图中获取该节点的邻接点
4、如果邻接点不在visit中，则将该邻接点加入queue和visit中
5、输出pop出的节点
6、重复3、4、5，直至队列为空
实现过程
如图：从A开始
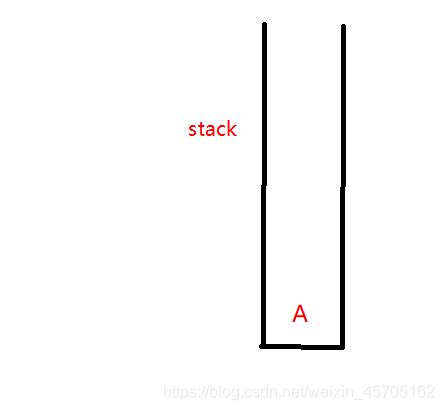
1、A进入队列
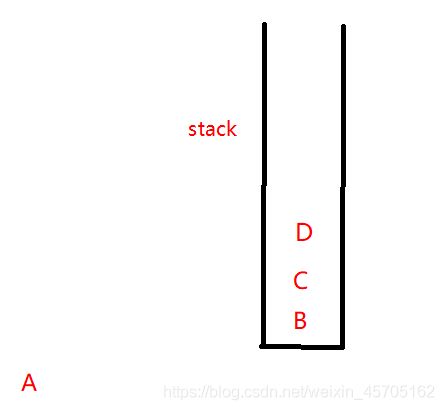
2、A出队列时，A的邻接结点B、C、D进入队列
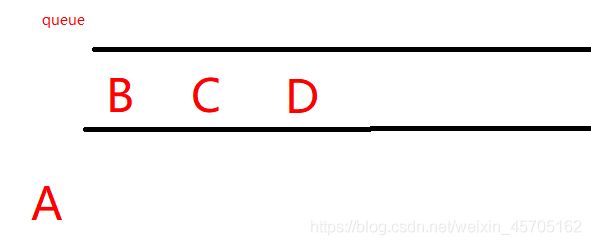
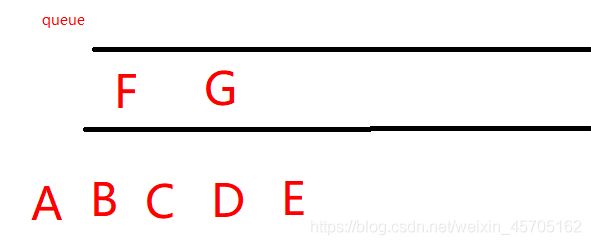
3、B出队列时，B的邻接结点A、E、F中未进过队列的E、F进入队列
4、C出队列时，C的邻接结点A、D、F、G、中未进过队列的G进入队列
5、D出队列时，D的邻接结点A、C、G已经全部进入过队列
6、E出队列，邻接结点均已进入过队列
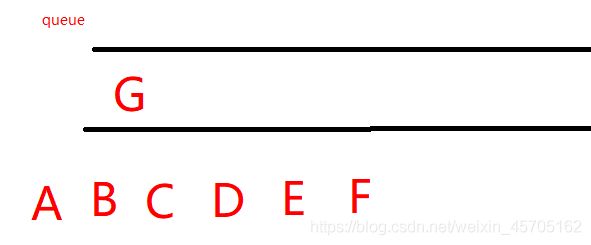
7、F出队列，邻接结点均已进入过队列
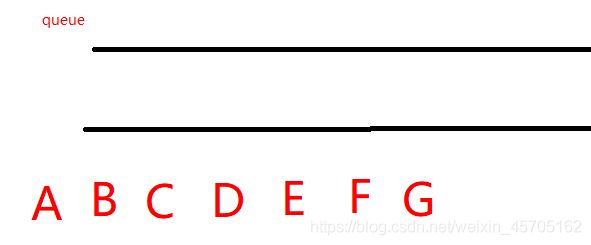
8、G出队列，邻接结点均已进入过队列
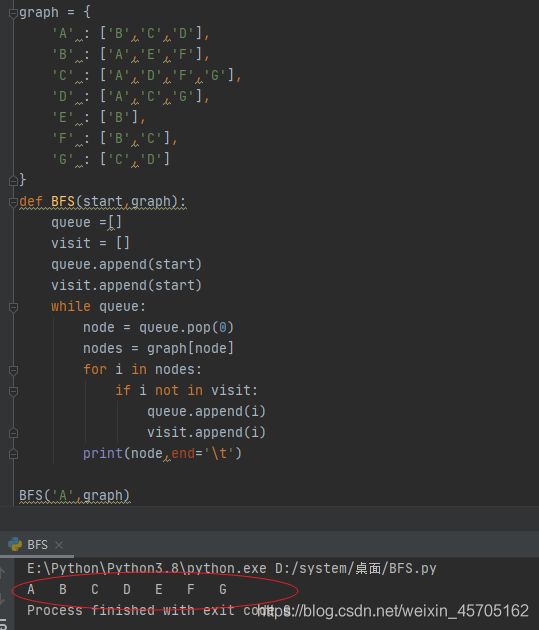
结果 ： A B C D E F G
Python代码实现
用字典结构表示
graph = {
'A' : ['B','C','D'],
'B' : ['A','E','F'],
'C' : ['A','D','F','G'],
'D' : ['A','C','G'],
'E' : ['B'],
'F' : ['B','C'],
'G' : ['C','D']
}
BFS
def BFS(start,graph):
queue =[]
visit = []
queue.append(start)
visit.append(start)
while queue:
node = queue.pop(0)
nodes = graph[node]
for i in nodes:
if i not in visit:
queue.append(i)
visit.append(i)
print(node,end='\t')
运行结果：
DFS算法
DFS沿着树的深度遍历树的节点，
选一条路一直走到底，回溯，遍历所有的子节点，进而达到全局搜索的目的。
算法思路
栈（先进后出）
和BFS相似，只是稍微做了一丝改变
1、创建一个空栈stack（用来存放节点）和一个空列表visit（用来存放已访问的节点）
2、依次将起始点及邻接点加入stack和visit中
3、poo出栈中最后进入的节点,从图中获取该节点的邻接点
4、如果邻接点不在visit中，则将该邻接点加入stack和visit中
5、输出pop出的节点
6、重复3、4、5，直至栈为空
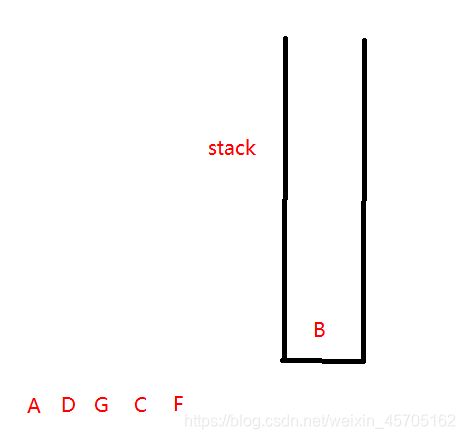
实现过程
如图：从A开始
1、A进入堆栈
2、A出堆栈时，A的邻接结点B、C、D进入堆栈
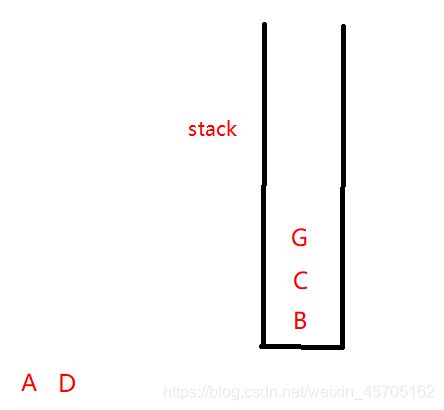
3、D出堆栈时，D的邻接结点A、C、G中未进过堆栈的G进入堆栈
4、G出堆栈时，G的邻接结点C、D已经全部进入过堆栈
5、C出堆栈时，C的邻接结点A、D、F、G中未进过堆栈的F进入堆栈
6、F出堆栈，邻接结点均已进入过堆栈
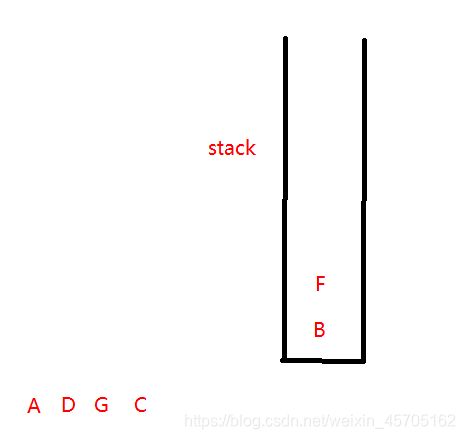
7、B出堆栈，邻接结点E进入堆栈
8、E出堆栈
结果 ： A D G C F B E
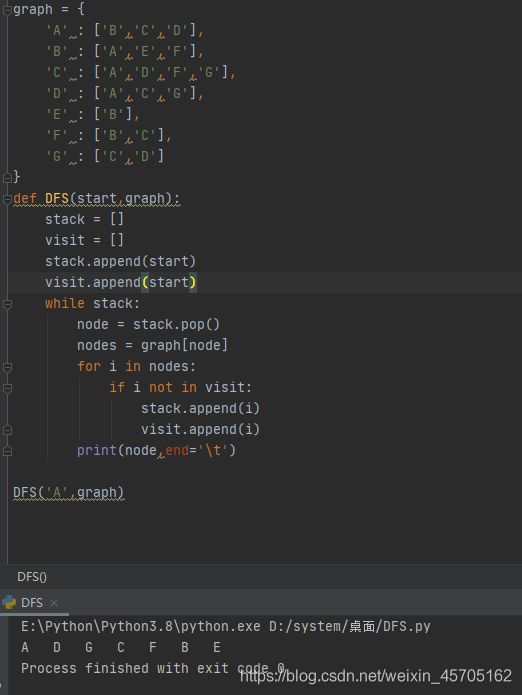
Python代码实现
graph = {
'A' : ['B','C','D'],
'B' : ['A','E','F'],
'C' : ['A','D','F','G'],
'D' : ['A','C','G'],
'E' : ['B'],
'F' : ['B','C'],
'G' : ['C','D']
}
def DFS(start,graph):
stack = []
visit = []
stack.append(start)
visit.append(start)
while stack:
node = stack.pop()
nodes = graph[node]
for i in nodes:
if i not in visit:
stack.append(i)
visit.append(i)
print(node,end='\t')
DFS('A',graph)
运行结果：
