C语言实现小波分解，提取近似与细节分量，包含详细例程

C语言实现小波分解，提取近似与细节分量，包含详细例程

声明

本文的C语言实现小波分解非本人原创，均参考了网络上的文章（详见最后的参考资料），程序主要来自李承宇的文章和程序。
我只对程序进行了少量的修改，添加了大量注释，提高了程序的可阅读性。

数据均为自己的数据，可以免费提供大家测试学习。

程序

main.c

// WaveletAccumulation.cpp : 定义控制台应用程序的入口点。
//

#include "stdafx.h"
#include <stdio.h>   
#include <stdlib.h>   
#include <math.h>   
#include "Wavelet.h" 

void main()
{
     
	double data[LENGTH] = {
      0 };		//输入信号   
	double temp[LENGTH] = {
      0 };		//中间结果   
	double data_output[LENGTH] = {
      0 };	//一维小波变换后的结果   
	double c[8][LENGTH] = {
      0 };		//各层的近似(前半段)与细节(后半段)
	double a[8][LENGTH] = {
      0 };		//各层的近似系数，第i行表示第i层分解的近似	Approximate
	double d[8][LENGTH] = {
      0 };		//各层的细节系数，第i行表示第i层分解的细节	Detail
	int sigLen = 0;					//输入信号长度   
	int waveletBasisLen = 6;					//Daubechies正交小波基长度   
	int nStep = 4;				//分解层数   

	FILE *fp;					//文件指针
	char s[32];					//从txt文件中读取一行数据

	/* matlab产生的 db3小波  */
	double Lo_D[] = {
      0.0352262918821007, -0.0854412738822415, -0.135011020010391, 0.459877502119331 , 0.806891509313339 , 0.332670552950957 };
	double Hi_D[] = {
      -0.332670552950957 ,  0.806891509313339 , -0.459877502119331, -0.135011020010391, 0.0854412738822415, 0.0352262918821007 };
	/* matlab产生的 db3小波  */
//	double Lo_D[] = {  0.00333572528500155, -0.0125807519990155, -0.00624149021301171, 0.0775714938400652, -0.0322448695850295, -0.242294887066190 ,  0.138428145901103 ,  0.724308528438574  , 0.603829269797473 , 0.160102397974125   };
//	double Hi_D[] = { -0.160102397974125  ,  0.603829269797473 , -0.724308528438574  , 0.138428145901103 ,  0.242294887066190 , -0.0322448695850295, -0.0775714938400652, -0.00624149021301171, 0.0125807519990155, 0.00333572528500155 };
	//matlab计算系数函数：[Lo_D,Hi_D,Lo_R,Hi_R] = wfilters('db1');

	waveletBasisLen = sizeof(Lo_D) / sizeof(double);

	//从文件读取输入信号   
	if ((fp = fopen("F:\\Desktop\\data.txt", "r")) == NULL)
	{
     
		printf("can't open file!\n");
		exit(0);
	}

	while (fgets(s, 32, fp) != NULL) //读取长度n要设置得长一点，要保证读到回车符，这样指针才会定位到下一行
	{
     
		data[sigLen] = atof(s);			//atof将字符串转换为数据
		sigLen++;
	}

	//关闭文件   
	fclose(fp);

	//一维小波变换   
	DWT1D(data, data_output, temp, Lo_D, Hi_D, sigLen, waveletBasisLen, nStep, c);

	//txt文件路径及文件名
	char *FilePath1 = "F:\\Desktop\\Result_1.txt";
	char *FilePath2 = "F:\\Desktop\\Result_2.txt";
	char *FilePath3 = "F:\\Desktop\\Result_3.txt";
	char *FilePath4 = "F:\\Desktop\\Result_4.txt";

	char* pFilePath[4] = {
      FilePath1, FilePath2, FilePath3, FilePath4 };	//指针数组，存放四个文件的文件路径和文件名

	for (int i = 0; i < nStep; i++)		//将各层变换的结果写入txt文件 
	{
     
		fp = fopen(pFilePath[i], "w");
		for (int j = 0; j < sigLen / pow(2, i); j++)			//pow(a,b)：是a的b次方
		{
     
			fprintf(fp, "%lf\n", c[i][j]);			//fprintf格式化输入到文件
		}
		fclose(fp);

		//将近似、细节分量分开存储
		int l = LENGTH / pow(2, i);
		for (int k = 0; k < l / 2; k++)
			a[i][k] = c[i][k];

		for (int k = l / 2; k <l; k++)
			d[i][k - l / 2] = c[i][k];
	}
}

Wavelet.h

#pragma once

#define LENGTH 2000//信号长度 

void DWT1D(double input[], double output[], double temp[], double Lo_D[],
	double Hi_D[], int sigLen, int m, int nStep, double c[8][LENGTH]);
	

Wavelet.cpp

#include "stdafx.h"
#include "Wavelet.h"  

#include <stdio.h>   
#include <stdlib.h>   
#include <math.h>   
/*****************************************************************
*　一维卷积函数
*
*　说明:
*  循环卷积,卷积结果的长度与输入信号的长度相同
*
*　输入参数:
*  data[],输入信号;
*  Lo_D[],Daubechies小波基低通滤波器系数;
*  Hi_D[],Daubechies小波基高通滤波器系数;
*  cov[],卷积结果;
*  n,输入信号长度;
*  m,卷积核长度.

*****************************************************************/
void Covlution(double data[], double Lo_D[], double Hi_D[], double cov[], int sigLen, int waveletBasisLen)
//					  output[]		 Lo_D[]		 Hi_D[]		 temp[]		sigLen	   m
{
     
	int i = 0, j = 0, k = 0;

	for (i = 0; i < sigLen; i++)			//将cov[]清零   
		cov[i] = 0;

	//****************************************************   
	//奇数行用Lo_D[]进行卷积   
	//****************************************************   
	//前m/2+1行   
	i = 0;
	for (j = 0; j < waveletBasisLen / 2; j += 2, i += 2)
	{
     
		for (k = waveletBasisLen / 2 - j; k < waveletBasisLen; k++)
			cov[i] += data[k - (waveletBasisLen / 2 - j)] * Lo_D[k];//k针对core[k]   

		for (k = sigLen - waveletBasisLen / 2 + j; k < sigLen; k++)
			cov[i] += data[k] * Lo_D[k - (sigLen - waveletBasisLen / 2 + j)];//k针对data[k]   
	}

	//中间的n-m行   
	for (; i <= (sigLen - waveletBasisLen) + waveletBasisLen / 2; i += 2)
	{
     
		for (j = 0; j < waveletBasisLen; j++)
			cov[i] += data[i - waveletBasisLen / 2 + j] * Lo_D[j];
	}

	//最后m/2-1行    
	for (j = 1; j <= waveletBasisLen / 2; j += 2, i += 2)
	{
     
		for (k = 0; k < j; k++)
			cov[i] += data[k] * Lo_D[waveletBasisLen - j - k];//k针对data[k]   

		for (k = 0; k < waveletBasisLen - j; k++)
			cov[i] += Lo_D[k] * data[sigLen - (waveletBasisLen - j) + k];//k针对core[k]   
	}

	//****************************************************   
	//偶数行用Hi_D[]进行卷积   
	//****************************************************   
	//前m/2+1行   
	i = 1;
	for (j = 0; j < waveletBasisLen / 2; j += 2, i += 2)
	{
     
		for (k = waveletBasisLen / 2 - j; k < waveletBasisLen; k++)
			cov[i] += data[k - (waveletBasisLen / 2 - j)] * Hi_D[k];//k针对core[k]   

		for (k = sigLen - waveletBasisLen / 2 + j; k < sigLen; k++)
			cov[i] += data[k] * Hi_D[k - (sigLen - waveletBasisLen / 2 + j)];//k针对data[k]   
	}

	//中间的n-m行   
	for (; i <= (sigLen - waveletBasisLen) + waveletBasisLen / 2; i += 2)
	{
     
		for (j = 0; j < waveletBasisLen; j++)
			cov[i] += data[i - waveletBasisLen / 2 + j] * Hi_D[j];
	}

	//最后m/2-1行   
	for (j = 1; j <= waveletBasisLen / 2; j += 2, i += 2)
	{
     
		for (k = 0; k < j; k++)
			cov[i] += data[k] * Hi_D[waveletBasisLen - j - k];//k针对data[k]   

		for (k = 0; k < waveletBasisLen - j; k++)
			cov[i] += Hi_D[k] * data[sigLen - (waveletBasisLen - j) + k];//k针对core[k]   
	}
}

/*****************************************************************
*   排序函数
*
*   将卷积后的结果进行排序，使尺度系数和小波系数分开
*****************************************************************/
void Sort(double data[], double sort[], int sigLen)
{
     
	for (int i = 0; i < sigLen; i += 2)
		sort[i / 2] = data[i];

	for (int i = 1; i < sigLen; i += 2)
		sort[sigLen / 2 + i / 2] = data[i];
}

/*****************************************************************
*　一维小波变换函数
*
*　说明:
*  一维小波变换,可进行多次分解,将每层的分解结果存入c[][]中
*
*　输入参数:
*  % input[],输入信号;
*  % output[],小波变换结果，包括尺度系数和小波系数两部分;
*  % temp[],存放中间结果;
*  % Lo_D[],Daubechies小波基低通滤波器系数;
*  % Hi_D[],Daubechies小波基高通滤波器系数;
*  % n,输入信号长度;
*  % m,Daubechies小波基紧支集长度;
*  % nStep,小波变换分解次数
*
*　李承宇, [email protected]
*
*  2010-08-22
*****************************************************************/
void DWT1D(double input[], double output[], double temp[], double Lo_D[],
	double Hi_D[], int sigLen, int waveletBasisLen, int nStep, double c[8][LENGTH])
{
     
	int i = 0, k = 0;

	for (i = 0; i < sigLen; i++)
		output[i] = input[i];						//初始化

	for (i = 0; i < nStep; i++)						//进行nStep层分解
	{
     
		Covlution(output, Lo_D, Hi_D, temp, sigLen, waveletBasisLen);		//卷积结果存放在temp[]中
		Sort(temp, output, sigLen); 						//使尺度系数和小波系数分开  	temp --> output

		for (k = 0; k < LENGTH / pow(2, i); k++)	//将每层的结构都存储到c[][]中
		{
     
			c[i][k] = output[k];
		}
		sigLen = sigLen / 2;									//每次分解后，信号长度减半
	}
}

需要说明几点

1. 程序中的小波基高低通滤波器系数可以通过matlab的wfilters函数来求得，例如：

[Lo_D,Hi_D,Lo_R,Hi_R] = wfilters(‘db1’)

2. 随着小波分解的层数增加，分解得到的结果长度越短；
   例如，2000点原始信号，一层分解后，近似和细节各只有1000点；二层分解后，近似和细节各只有500点；以此类推。

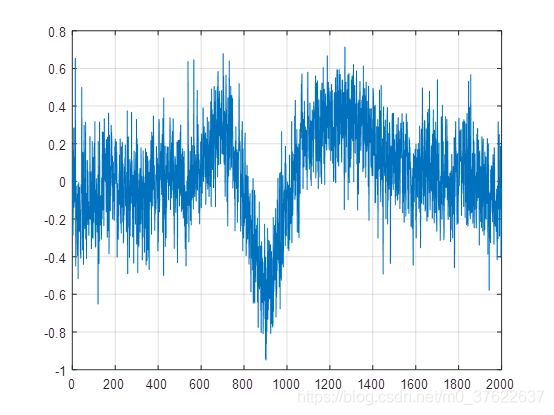
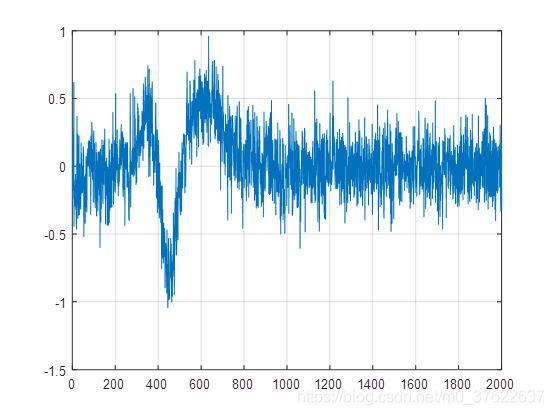
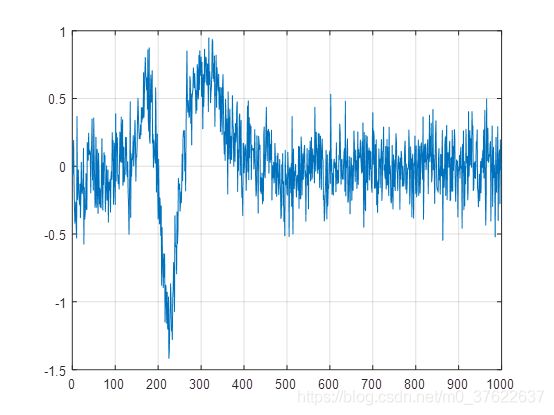
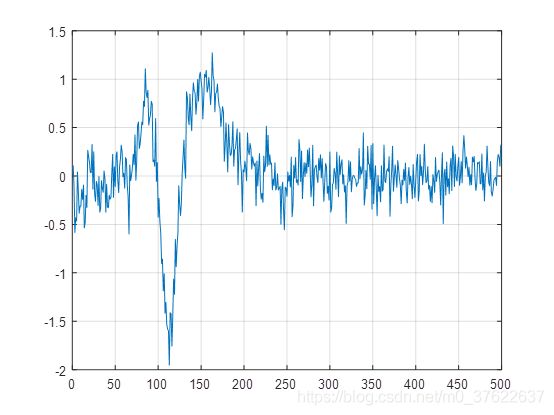
3. 本程序，将近似和细节结果都存放在了一个数组，我在画图的时候也没有分来来画，所以后面例子的前半段为近似分量，后半段为细节分量，再次说明一下。

例子

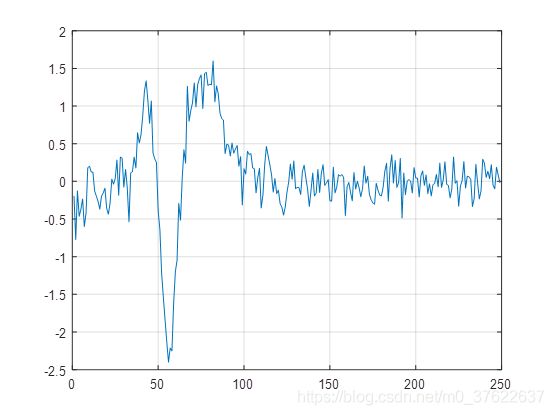
原始信号输入：

共2000点的原始信号。

第一层分解：

前1000点为近似分量；后1000点为细节分量。

第二层分解

前500点为近似分量；后500点为细节分量。

第三层分解

前250点为近似分量；后250点为细节分量。

第四层分解

前125点为近似分量；后125点为细节分量。

例程数据和程序下载地址

https://download.csdn.net/download/m0_37622637/11561236

参考资料

[1]小波变换c语言程序-百度文库
[2]CSDN资料下载
[3]C语言实现一维小波变换