最短路板子及小结
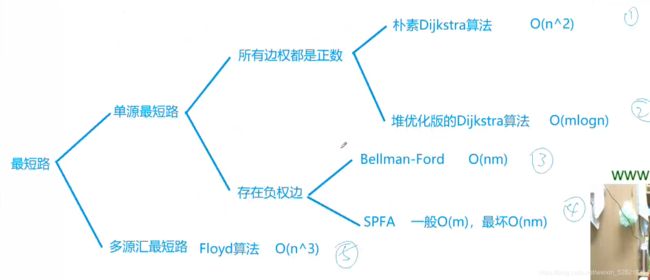
最短路总结
1.堆优化dijkstra算法求单源非负权最短路
可以解决自环,重边,但边权必须为非负数 用的vector存边
const int maxn=1e5+86;
int a[maxn],dis[maxn],vis[maxn];
int n,m;
struct edge{
int to,dis;
};
vectorg[maxn];
struct edge1{
int id,dis;
bool operator<(const edge1&rhs )const{
return dis>rhs.dis;
}
};
priority_queueqwq;
void dijkstra(int q){
memset(dis,1e9,sizeof(dis));
while(!qwq.empty()) qwq.pop();
qwq.push({
q,0});
while(!qwq.empty()){
edge1 now=qwq.top();
qwq.pop();
if(vis[now.id]==1) continue;
for(int i=0;isize();i++){
int to=g[now.id][i].to;
int dis1=g[now.id][i].dis;
if(dis[to]>now.dis+dis1){
dis[to]=now.dis+dis1;
qwq.push({
to,dis[to]});
}
}
vis[now.id]=1;
}
}
2.SPFA算法求单源负权最短路
单源最短路可以解决重边和自环,边权为负值 用的是vector存边
const int maxn = 1e5 + 86;
bool vis[maxn];
int dis[maxn];
struct edge {
int to, dis;
};
vector< edge >g[maxn];
int n, m;
void spfa(int x) {
queueqwq;
qwq.push( x );
for (int i = 1; i <= n; i++) dis[i] = 1e9;
dis[x] = 0;
while (!qwq.empty()) {
int now = qwq.front();
vis[now] = 0;
qwq.pop();
for (int i = 0; i < g[now].size(); i++) {
int to = g[now][i].to;
int dis1 = g[now][i].dis;
if (dis[to] > dis1 + dis[now]) {
dis[to] = dis1 + dis[now];
if (!vis[to]) {
qwq.push(to);vis[to] = 1;
}
}
}
}
}
这一份是用链式前向星存图的spfa板子
const int maxn = 1e5 + 86;
struct edge1 {
int to, next, w;
}edge[maxn];
int cnt, n, m;
int head[maxn], dis[maxn], vis[maxn];
void add(int from, int to, int dis) {
edge[++cnt].next = head[from];
edge[cnt].to = to;
edge[cnt].w = dis;
head[from] = cnt;
}//将head数组先全部初始化为0
void spfa(int s) {
for (int i = 1; i <= n; i++) dis[i] = 1e9;
memset(vis, 0, sizeof(vis));
dis[s] = 0;
vis[s] = 1;
queue<int>qwq;
qwq.push(s);
while (!qwq.empty()) {
int now = qwq.front();
qwq.pop();
vis[now] = 0;
for (int i = head[now]; i; i = edge[i].next) {
int to = edge[i].to;
int dis1 = edge[i].w;
if (dis[to] > dis[now] + dis1) {
dis[to] = dis[now] + dis1;
if (!vis[to]) {
vis[to] = 1;
qwq.push(to);
}
}
}
}
}
用spfa来判断负环 用一个数组num[ ]就可以了
const int maxn = 1e5 + 86;
struct edge1 {
int to, next, w;
}edge[maxn];
int cnt, n, m, k;
int head[maxn], dis[maxn], vis[maxn], num[maxn];
void add(int from, int to, int dis) {
edge[++cnt].next = head[from];
edge[cnt].to = to;
edge[cnt].w = dis;
head[from] = cnt;
}
bool spfa( ) {
for (int i = 1; i <= n; i++) dis[i] = 1e9;
memset(vis, 0, sizeof(vis));
queue<int>qwq;
for (int i = 1; i <= n; i++) {
qwq.push(i);
vis[i] = 1;
}
while (!qwq.empty()) {
int now = qwq.front();
qwq.pop();
vis[now] = 0;
for (int i = head[now]; i; i = edge[i].next) {
int to = edge[i].to;
int dis1 = edge[i].w;
if (dis[to] > dis[now] + dis1) {
num[to] = num[now] + 1;
dis[to] = dis[now] + dis1;
if (!vis[to]) { vis[to] = 1; qwq.push(to);}
if (num[to] >= n) return true;
}
}
}
return false;
}
3.Bellman-Ford算法求单源有限制边数的最短路
k是限制边数,可以解决边权为负
const int N = 510, M = 10010, INF = 0x3f3f3f3f;
int n, m, k;
int dis[N];
int backup[N];
struct Edges {
int a, b, w;
}edge[M];
int bellman_ford(){
memset(dis, 0x3f, sizeof dis);
dis[1] = 0;
for (int i = 0; i < k; i++) {
memcpy(backup, dis, sizeof dis);
for (int j = 0; j < m; j++) {
int a = edge[j].a, b = edge[j].b, w = edge[j].w;
dis[b] = min(dis[b], backup[a] + w);
}
}
if (dis[n] > INF / 2) return INF;
else return dis[n];
}
4.floyd算法求多源最短路
可以解决重边,自环,负边权,不可以解决负环
const int maxn = 1e3 + 86, INF = 1e9;
int n, m, k;
int dis[maxn][maxn];
void floyd() {
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
dis[i][j] = min(dis[i][j], dis[i][k] + dis[k][j]);
}
}
}
}