python数据分析与挖掘实战—第3章(数据探索)
通过检验数据集的数据质量、绘制图表、计算某些特征量等手段,对样本数据集的结构和规律进行分析的过程就是数据探索。数据探索有助于选择合适的数据预处理和建模方法,甚至可以完成一些通常由数据挖掘解决的问题。
3.1 数据质量分析
数据质量分析的主要任务是检查原始数据中是否存在脏数据
1. 缺失值
使用简单的统计分析,可以得到含有缺失值的属性的个数,以及每个属性的未缺失数、缺失数与缺失率。从总体上来说,缺失值的处理分为删除存在缺失值的记录、对可能值进行插补和不处理3种情况。
2. 异常值
- 简单统计量分析(描述性统计,进而查看哪些数据不合理,例如最大值和最小值)
- 3σ原则(3倍标准差)
- 箱线图分析(小于上四分位数-1.5四分位数间距或大于上四分位数+1.5四分位数间距)
3. 不一致的值
数据不一致性是指数据的矛盾性、不相容性。例如,两张表中都储存了用户的电话号码,但在用户的电话号码发生改变时只更新了一张表中的数据。
4. 重复数据及含有特殊符号的数据
案例:分析餐饮系统的销量额数据
import pandas as pd
import matplotlib.pylab as plt
%matplotlib
catering_sale = 'G:/Python数据分析与挖掘实战/chapter3/demo/data/catering_sale.xls' #餐饮数据
data = pd.read_excel(catering_sale,index_col='日期') #读取数据,指定”日期“列为索引列
print(len(data))
print(data.describe())
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
plt.figure()
p = data.boxplot(return_type='dict') #箱线图
x = p['fliers'][0].get_xdata() #‘fliers’为异常值的标签
y = p['fliers'][0].get_ydata()
y.sort() #从小到大排序,该方法直接改变原对象
#用annotate添加注释
#其中有些相近的点,注解会出现重叠,难以看清,需要一些技巧来控制
for i in range(len(x)):
if i > 0:
plt.annotate(y[i],xy=(x[i],y[i]),xytext=(x[i]+0.05-0.8/(y[i]-y[i-1]),y[i]))
else:
plt.annotate(y[i],xy=(x[i],y[i]),xytext=(x[i]+0.08,y[i]))
plt.show()
输出结果:
201
销量
count 200.000000
mean 2755.214700
std 751.029772
min 22.000000
25% 2451.975000
50% 2655.850000
75% 3026.125000
max 9106.440000
- 缺失值个数:1
- 箱线图中的超过上下界的8个销售额数据可能为异常值,结合具体业务可以把865、4060.3、4065.2归为正常值,将22、51、60、6607.4、9106.44归为异常值
- 最后确定过滤规则为:日销量在400以下5000以上则属于异常数据,编写过滤程序,进行后续处理
3.2 数据特征分析
1.分布分析
分布分析能揭示数据的分布特征和分布类型
- 定量数据:频率分布表、频率分布直方图、茎叶图
- 定性分类数据:饼图、条形图
2.对比分析
对比分析是指把两个相互联系的指标进行比较,从数量上展示和说明研究对象规模的大小,水平的高低,速度的快慢,以及各种关系是否协调。
- 绝对数比较
- 相对数比较:结构、比例、比较、强度、计划完成程度、动态
3. 统计量分析
- 集中趋势:均值、中位数、众数
- 离中趋势:极差、标准差(方差)、变异系数、四分位间距
4. 周期性分析
周期性分析是探索某个变量是否随着时间变化而呈现出某种周期变化趋势
5.贡献度分析
贡献度分析又称帕累托分析,它的原理是帕累托法则,又称20/80定律。同样的投入放在不同的地方会产生不同的效益。例如,对一个公司来讲,80%的利润常常来自于20%最畅销的产品,而其他80%的产品只产生了20%的利润
6.相关性分析
分析连续变量之间线性相关程度的强弱
- 散点图
- 散点图矩阵
- 相关系数(Pearson相关系数、Spearman秩相关系数、判定系数)
案例:分析餐饮系统的销量额数据(接上)
统计量分析
#餐饮销量数据统计量分析
catering_sale = 'G:/Python数据分析与挖掘实战/chapter3/demo/data/catering_sale.xls' #餐饮数据
data = pd.read_excel(catering_sale,index_col='日期') #读取数据,指定”日期“列为索引列
data_1 = data[(data[u'销量'] > 400)&(data[u'销量'] < 5000)] #过滤异常数据
statistics = data_1.describe() #保存基本统计量
statistics.loc['range'] = statistics.loc['max'] - statistics.loc['min'] #极差
statistics.loc['variation'] = statistics.loc['std'] / statistics.loc['mean'] #变异系数
statistics.loc['dis'] = statistics.loc['75%'] - statistics.loc['25%'] #四分位数间距
print(statistics)
输出结果:
销量
count 195.000000
mean 2744.595385
std 424.739407
min 865.000000
25% 2460.600000
50% 2655.900000
75% 3023.200000
max 4065.200000
range 3200.200000
variation 0.154755
dis 562.600000
贡献度分析
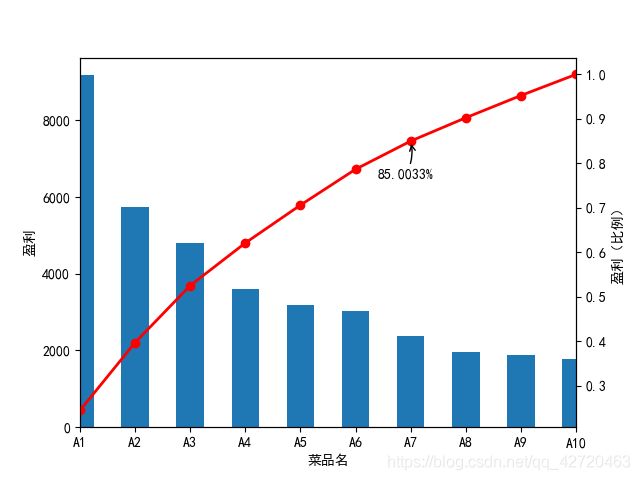
#菜品盈利数据 帕累托图
from __future__ import print_function
import pandas as pd
#初始化参数
dish_profit = 'G:/Python数据分析与挖掘实战/chapter3/demo/data/catering_dish_profit.xls'
data = pd.read_excel(dish_profit,index_col='菜品名')
data = data['盈利'].copy()
data.sort_values(ascending=False)
import matplotlib.pylab as plt
%matplotlib
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
plt.figure()
data.plot(kind='bar')
plt.ylabel('盈利')
p = 1.0*data.cumsum()/data.sum()
p.plot(color='r',secondary_y=True,style='-o',linewidth=2)
plt.annotate(format(p[6],'.4%'),xy=(6,p[6]),xytext=(6*0.9,p[6]*0.9),arrowprops=dict(arrowstyle="->",
connectionstyle='arc3,rad=.2'))
#添加注释,即85%处的标记
plt.ylabel('盈利(比例)')
plt.show()
- 菜品A1-A7共7个菜品,占菜品种类数的70%,总盈利额占该月盈利额的85.0033%
- 根据帕累托法则,应该增加对菜品A1-A7的成本投入,减少对菜品A8-A10的投入以获得更高的盈利额
相关性分析
import pandas as pd
catering_sale = 'G:/Python数据分析与挖掘实战/chapter3/demo/data/catering_sale_all.xls'
data = pd.read_excel(catering_sale,index_col='日期')
print('相关系数矩阵:\n',data.corr())
print('百合酱蒸凤爪与其他菜式的相关系数:\n',data.corr()["百合酱蒸凤爪"])
print("百合酱蒸凤爪与翡翠蒸香茜饺的相关系数:\n",data['百合酱蒸凤爪'].corr(data['翡翠蒸香茜饺']))
输出结果(部分):
百合酱蒸凤爪与其他菜式的相关系数:
百合酱蒸凤爪 1.000000
翡翠蒸香茜饺 0.009206
金银蒜汁蒸排骨 0.016799
乐膳真味鸡 0.455638
蜜汁焗餐包 0.098085
生炒菜心 0.308496
铁板酸菜豆腐 0.204898
香煎韭菜饺 0.127448
香煎罗卜糕 -0.090276
原汁原味菜心 0.428316
Name: 百合酱蒸凤爪, dtype: float64
百合酱蒸凤爪与翡翠蒸香茜饺的相关系数:
0.009205803051836475
从上面的结果可以看到,如果顾客点了“百合酱蒸凤爪”,则和点“翡翠蒸香茜饺” “金银蒜汁蒸排骨” “香煎罗卜糕”等主食类的相关性比较低,反而点“乐膳真味鸡” “生炒菜心” “原汁原味菜心”的相关性比较高