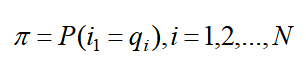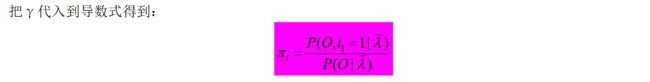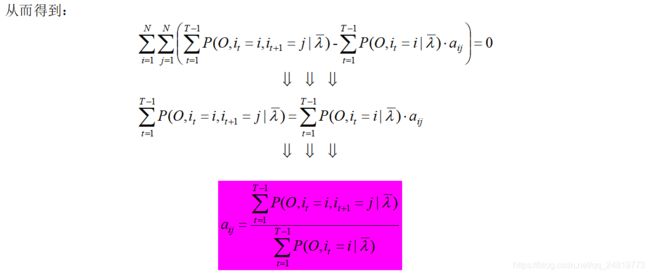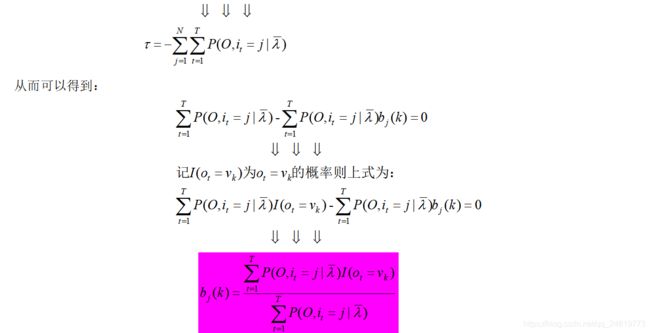统计学习方法学习笔记9——隐马尔科夫模型（HMM原理推导分析与分词项目实践）

目录

1.简介

2.概率计算方法

2.1、模型参数的介绍

 2.1.1、初始概率

2.1.2、状态转移矩阵

2.1.3、观测概率矩阵

2.2、前向-后向算法

2.2.1、前向算法

2.2.2、后向算法

2.2.3、前向算法与后向算法的关系

3、HMM的训练/学习问题

3.1、Baum-Welch算法

3.2、Baum-Welch算法伪代码

4、预测问题：Viterbi算法——动态规划思想

5.实践部分——HMM对中文进行分词

5.1、定义计算概率相关的函数

5.2、训练算法的相关函数

5.3、文件处理相关的函数

5.4、训练函数

5.5、预测算法函数

5.6、进行分词操作

5.7、执行

5.8、文档内容为

5.9、分词结果

6.代码和文件的地址

---

1.简介

隐马尔科夫模型（Hidden Markov Model,HMM），可用于标注问题的统计学习模型，描述由隐藏的马尔科夫链随机生成观测序列的过程。

HMM属于生成模型。

应用领域：语音识别、自然语言处理（NLP）、生物信息、模式识别等领域。

主要过程：概率计算方法（直接计算法、前向算法、后向算法）==>学习算法（Baum-Welch EM算法）==>预测算法（Viterbi算法）

2.概率计算方法

2.1、模型参数的介绍

 2.1.1、初始概率

                    是指在时刻t=1，状态qi发生的概率。

2.1.2、状态转移矩阵

：在时刻t出状态qi发生的条件下，时刻t+1转移到状态qj的概率，如下图。

2.1.3、观测概率矩阵

:是指在时刻t，状态qi发生的条件下，生成观测vk的概率，如上图。

2.2、前向-后向算法

由于直接计算法属于暴力求解的方法，时间复杂度非常高，对于计算机来说计算非常费时间，在这里选择实践复杂度比较小的前向-后向算法。其实前向-后向算法的思想也是来源于动态规划的思想。

2.2.1、前向算法

2.2.2、后向算法

2.2.3、前向算法与后向算法的关系

3、HMM的训练/学习问题

3.1、Baum-Welch算法

3.2、Baum-Welch算法伪代码

4、预测问题：Viterbi算法——动态规划思想

Viterbi算法实际式用动态规划求解HMM预测问题，用DP求解概率最大的路径也就式最优路径，每个路径对应一个状态序列。

5.实践部分——HMM对中文进行分词

5.1、定义计算概率相关的函数

def log_normalize(a):
    s = 0
    for x in a:
        s += x
    s = math.log(s)
    for i in range(len(a)):
        if a[i] == 0:
            a[i] = infinite
        else:
            a[i] = math.log(a[i]) - s

def log_sum(a):
    if not a:   # a为空
        return infinite
    m = max(a)
    s = 0
    for t in a:
        s += math.exp(t-m)
    return m + math.log(s)

def calc_alpha(pi, A, B, o, alpha):
    for i in range(4):
        alpha[0][i] = pi[i] + B[i][ord(o[0])]
    T = len(o)
    temp = [0 for i in range(4)]
    del i
    for t in range(1, T):
        for i in range(4):
            for j in range(4):
                temp[j] = (alpha[t-1][j] + A[j][i])
            alpha[t][i] = log_sum(temp)
            alpha[t][i] += B[i][ord(o[t])]

def calc_beta(pi, A, B, o, beta):
    T = len(o)
    for i in range(4):
        beta[T-1][i] = 1
    temp = [0 for i in range(4)]
    del i
    for t in range(T-2, -1, -1):
        for i in range(4):
            beta[t][i] = 0
            for j in range(4):
                temp[j] = A[i][j] + B[j][ord(o[t+1])] + beta[t+1][j]
            beta[t][i] += log_sum(temp)

def calc_gamma(alpha, beta, gamma):
    for t in range(len(alpha)):
        for i in range(4):
            gamma[t][i] = alpha[t][i] + beta[t][i]
        s = log_sum(gamma[t])
        for i in range(4):
            gamma[t][i] -= s

def calc_ksi(alpha, beta, A, B, o, ksi):
    T = len(alpha)
    temp = [0 for x in range(16)]
    for t in range(T-1):
        k = 0
        for i in range(4):
            for j in range(4):
                ksi[t][i][j] = alpha[t][i] + A[i][j] + B[j][ord(o[t+1])] + beta[t+1][j]
                temp[k] =ksi[t][i][j]
                k += 1
        s = log_sum(temp)
        for i in range(4):
            for j in range(4):
                ksi[t][i][j] -= s

5.2、训练算法的相关函数

def bw(pi, A, B, alpha, beta, gamma, ksi, o):
    T = len(alpha)
    for i in range(4):
        pi[i] = gamma[0][i]
    s1 = [0 for x in range(T-1)]
    s2 = [0 for x in range(T-1)]
    for i in range(4):
        for j in range(4):
            for t in range(T-1):
                s1[t] = ksi[t][i][j]
                s2[t] = gamma[t][i]
            A[i][j] = log_sum(s1) - log_sum(s2)
    s1 = [0 for x in range(T)]
    s2 = [0 for x in range(T)]
    for i in range(4):
        for k in range(65536):
            if k % 5000 == 0:
                print(i, k)
            valid = 0
            for t in range(T):
                if ord(o[t]) == k:
                    s1[valid] = gamma[t][i]
                    valid += 1
                s2[t] = gamma[t][i]
            if valid == 0:
                B[i][k] = -log_sum(s2)  # 平滑
            else:
                B[i][k] = log_sum(s1[:valid]) - log_sum(s2)

def baum_welch(pi, A, B):
    f = file("./2.txt")
    sentence = f.read()[3:].decode('utf-8') # 跳过文件头
    f.close()
    T = len(sentence)   # 观测序列
    alpha = [[0 for i in range(4)] for t in range(T)]
    beta = [[0 for i in range(4)] for t in range(T)]
    gamma = [[0 for i in range(4)] for t in range(T)]
    ksi = [[[0 for j in range(4)] for i in range(4)] for t in range(T-1)]
    for time in range(100):
        print "time:", time
        calc_alpha(pi, A, B, sentence, alpha)    # alpha(t,i):给定lamda，在时刻t的状态为i且观测到o(1),o(2)...o(t)的概率
        calc_beta(pi, A, B, sentence, beta)      # beta(t,i)：给定lamda和时刻t的状态i，观测到o(t+1),o(t+2)...oT的概率
        calc_gamma(alpha, beta, gamma)           # gamma(t,i)：给定lamda和O，在时刻t状态位于i的概率
        calc_ksi(alpha, beta, A, B, sentence, ksi)    # ksi(t,i,j)：给定lamda和O，在时刻t状态位于i且在时刻i+1，状态位于j的概率
        bw(pi, A, B, alpha, beta, gamma, ksi, sentence) #baum_welch算法

5.3、文件处理相关的函数

def list_write(f, v):
    for a in v:
        f.write(str(a))
        f.write(' ')
    f.write('\n')


def save_parameter(pi, A, B, time):
    f_pi = open("./pi%d.txt" % time, "w")
    list_write(f_pi, pi)
    f_pi.close()
    f_A = open("./A%d.txt" % time, "w")
    for a in A:
        list_write(f_A, a)
    f_A.close()
    f_B = open("./B%d.txt" % time, "w")
    for b in B:
        list_write(f_B, b)
    f_B.close()

    
def load_train():
    f = open("./pi.txt", mode="r")
    for line in f:
        pi = list(map(float, line.split(' ')[:-1]))
    f.close()

    f = open("./A.txt", mode="r")
    A = [[] for x in range(4)] # 转移矩阵：B/M/E/S
    i = 0
    for line in f:
        A[i] = list(map(float, line.split(' ')[:-1]))
        i += 1
    f.close()

    f = open("./B.txt", mode="r")
    B = [[] for x in range(4)]
    i = 0
    for line in f:
        B[i] = list(map(float, line.split(' ')[:-1]))
        i += 1
    f.close()
    return pi, A, B

5.4、训练函数

def train():
    # 初始化pi,A,B
    pi = [random.random() for x in range(4)]    # 初始分布
    log_normalize(pi)
    A = [[random.random() for y in range(4)] for x in range(4)] # 转移矩阵：B/M/E/S
    A[0][0] = A[0][3] = A[1][0] = A[1][3]\
        = A[2][1] = A[2][2] = A[3][1] = A[3][2] = 0 # 不可能事件
    B = [[random.random() for y in range(65536)] for x in range(4)]
    for i in range(4):
        log_normalize(A[i])
        log_normalize(B[i])
    baum_welch(pi, A, B)
    return pi, A, B

5.5、预测算法函数

def viterbi(pi, A, B, o):
    T = len(o)   # 观测序列
    delta = [[0 for i in range(4)] for t in range(T)]
    pre = [[0 for i in range(4)] for t in range(T)]  # 前一个状态   # pre[t][i]：t时刻的i状态，它的前一个状态是多少
    for i in range(4):
        delta[0][i] = pi[i] + B[i][ord(o[0])]
    for t in range(1, T):
        for i in range(4):
            delta[t][i] = delta[t-1][0] + A[0][i]
            for j in range(1,4):
                vj = delta[t-1][j] + A[j][i]
                if delta[t][i] < vj:
                    delta[t][i] = vj
                    pre[t][i] = j
            delta[t][i] += B[i][ord(o[t])]
    decode = [-1 for t in range(T)]  # 解码：回溯查找最大路径
    q = 0
    for i in range(1, 4):
        if delta[T-1][i] > delta[T-1][q]:
            q = i
    decode[T-1] = q
    for t in range(T-2, -1, -1):
        q = pre[t+1][q]
        decode[t] = q
    return decode

5.6、进行分词操作

def segment(sentence, decode):
    N = len(sentence)
    i = 0
    while i < N:  #B/M/E/S
        if decode[i] == 0 or decode[i] == 1:  # Begin
            j = i+1
            while j < N:
                if decode[j] == 2:
                    break
                j += 1
            print(sentence[i:j+1], "|",)
            i = j+1
        elif decode[i] == 3 or decode[i] == 2:    # single
            print(sentence[i:i+1], "|",)
            i += 1
        else:
            print('Error:', i, decode[i])
            i += 1

5.7、执行

if __name__ == "__main__":
    pi, A, B = load_train()
    f = open("./24.mybook.txt",'rb')
    data = f.read()[3:].decode('utf-8')
    f.close()
    decode = viterbi(pi, A, B, data)
    segment(data, decode)

5.8、文档内容为

5.9、分词结果

6.代码和文件的地址

链接：https://pan.baidu.com/s/1RwcEt6qXxwwGhrqrciFuaQ 
             提取码：k3pp