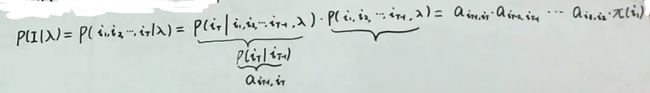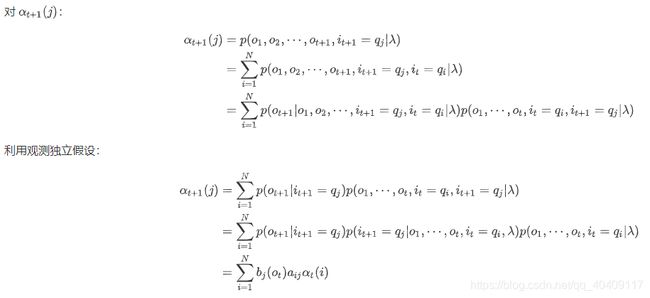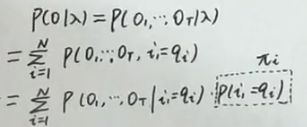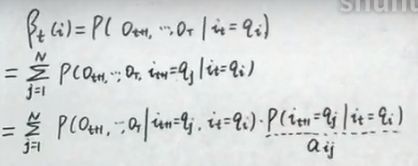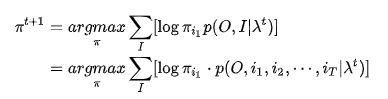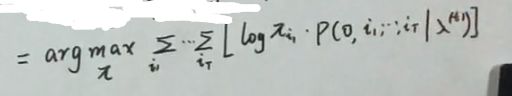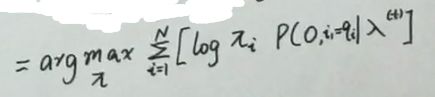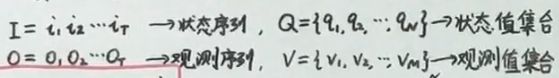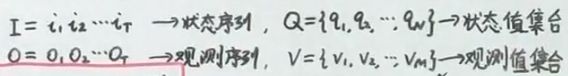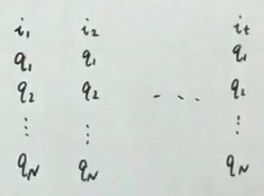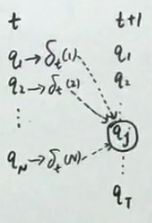隐马尔可夫模型(HMM)个人笔记整理
隐马尔可夫模型(HMM)
本文源自于笔记整理
参考资料如下:
发现一个大佬的笔记 全系列都有
https://www.yuque.com/books/share/f4031f65-70c1-4909-ba01-c47c31398466?#
机器学习白板推导系列:
https://www.bilibili.com/video/BV1MW41167Rf
1.背景介绍
可以看这个 HMM概述:
https://blog.csdn.net/weixin_30642869/article/details/97254733
HMM在DL前中的NLP占据重要的地位
机器学习:
1.频率派——统计机器学习:核心问题是优化问题,把loss function定义出来:
1)定义model
2)strategy: loss function
3)求解;algorithm: GD SGD 牛顿法 拟牛顿法
2.贝叶斯派——概率图模型:核心问题是推断,求后验概率,引申为积分问题,可以采用数值积分方法 MCMC(蒙特卡洛方法)求解
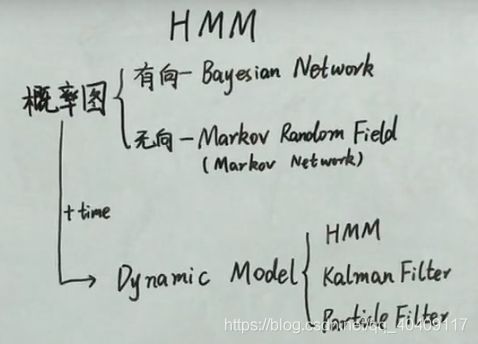
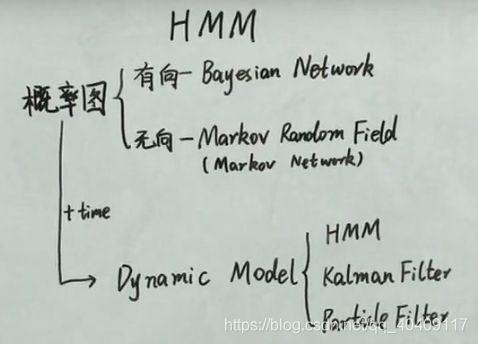
HMM属于概率图模型
概率图根据有向图和无向图分为两种:
有向:BN
无相MRF(MN)
加入了时间这个因素后,变为动态模型:HMM、卡尔曼滤波、粒子滤波等模型
我们通常说的模型,例如GMM高斯混合模型
有N个样本 x1…xN 独立同分布于一个概率分布
但是动态模型,就可以认为是普通模型加上了时间序列(这个"时间"可以是真正的时间,可以是一个抽象的,可以是一段话一个句子一个序列)
这种动态模型的特点:
(1)样本与样本之间不是iid(独立同分布)
(2)往往是混合的。
往往含有观测变量和系统状态(又叫隐变量)
从这个图来看 动态模型包含两个层面的东西:
(1)时间time(体现在图的横向随"时间"的变换)
(2)混合mixture(体现在观测变量和隐变量的关系)
进一步对动态模型按系统状态来划分:
系统状态为离散:HMM
系统状态为连续:线性:KF Kalman Filter
非线性:PF Particle Filter
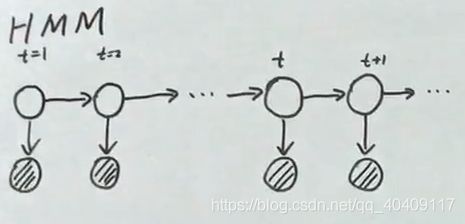
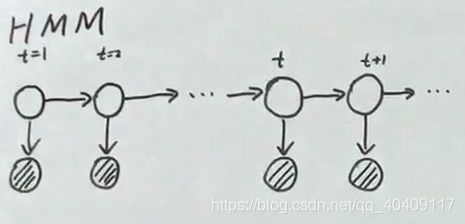
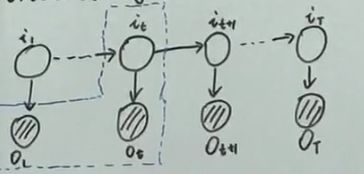
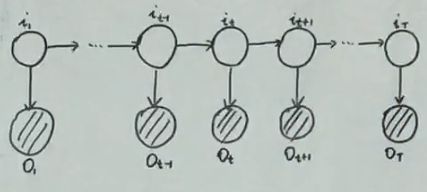
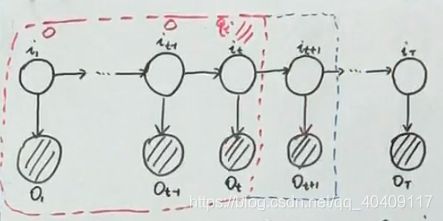
HMM的概率图:
一般用阴影结点表示观测变量 白色的结点表示隐变量
time + mixture
模型表达形式:
λ = ( π , A , B ) \lambda=(\pi,A,B) λ=(π,A,B)
π A B是三个参数
λ就表示HMM的参数,在这里是一个由π A B组成的三元组
π是初始概率分布
A是状态转移矩阵 transition matrix
B是发射矩阵 emission matrix 表达状态变量到观测变量间的关系
我们用以下符号表示:
下面使用 o t o_t ot 表示观测变量, O O O 为观测序列, V = { v 1 , v 2 , ⋯ , v M } V=\{v_1,v_2,\cdots,v_M\} V={ v1,v2,⋯,vM} 表示观测的值域, i t i_t it 表示状态变量, I I I 为状态序列, Q = { q 1 , q 2 , ⋯ , q N } Q=\{q_1,q_2,\cdots,q_N\} Q={ q1,q2,⋯,qN} 表示状态变量的值域。定义 A = ( a i j = p ( i t + 1 = q j ∣ i t = q i ) ) A=(a_{ij}=p(i_{t+1}=q_j|i_t=q_i)) A=(aij=p(it+1=qj∣it=qi)) 表示状态转移矩阵, B = ( b j ( k ) = p ( o t = v k ∣ i t = q j ) ) B=(b_j(k)=p(o_t=v_k|i_t=q_j)) B=(bj(k)=p(ot=vk∣it=qj)) 表示发射矩阵。
aij表示t时刻,状态i转移到j的概率
bj(k)表示观测为qj时,状态为vk的概率
HMM中的两个假设:
(1)齐次markov假设
即无后效性:
给定当前时刻,未来与过去无关,只依赖于当前。
用数学表达式表达为:
p ( i t + 1 ∣ i t , i t − 1 , ⋯ , i 1 , o t , o t − 1 , ⋯ , o 1 ) = p ( i t + 1 ∣ i t ) p(i_{t+1}|i_t,i_{t-1},\cdots,i_1,o_t,o_{t-1},\cdots,o_1)=p(i_{t+1}|i_t) p(it+1∣it,it−1,⋯,i1,ot,ot−1,⋯,o1)=p(it+1∣it)
(2)观测独立假设
p ( o t ∣ i t , i t − 1 , ⋯ , i 1 , o t − 1 , ⋯ , o 1 ) = p ( o t ∣ i t ) p(o_t|i_t,i_{t-1},\cdots,i_1,o_{t-1},\cdots,o_1)=p(o_t|i_t) p(ot∣it,it−1,⋯,i1,ot−1,⋯,o1)=p(ot∣it)
HMM要解决的三个问题:
Evaluation问题: p ( O ∣ λ ) p(O|\lambda) p(O∣λ),常用算法为 前向/后向算法
learning问题: λ = a r g m a x λ p ( O ∣ λ ) \lambda=\mathop{argmax}\limits_{\lambda}p(O|\lambda) λ=λargmaxp(O∣λ),常用算法为 EM算法(Bomm Welch)
decoding问题: I = a r g m a x I p ( I ∣ O , λ ) I=\mathop{argmax}\limits_{I}p(I|O,\lambda) I=Iargmaxp(I∣O,λ),找到一个状态序列I(O是观测序列),使得 P ( I ∣ O ) P(I|O) P(I∣O)最大,常用算法为Viterbi算法
decoding问题可以进一步细分为:
(1)预测问题:已知O,求 p ( i t + 1 ∣ o 1 , o 2 , ⋯ , o t ) p(i_{t+1}|o_1,o_2,\cdots,o_t) p(it+1∣o1,o2,⋯,ot) 即已知观测序列,预测下一个时刻的隐状态
(2)滤波问题,已知O,求 p ( i t ∣ o 1 , o 2 , ⋯ , o t ) p(i_t|o_1,o_2,\cdots,o_t) p(it∣o1,o2,⋯,ot) 即已知O,求it
【一般HMM不会求滤波问题 一般是动态模型中的Kalman Filter和Particle Filter来求】
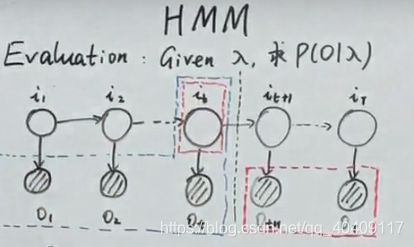
再回顾一下这个图
2.evaluation问题——前向算法
Evaluation问题:given λ,求P(O|λ)
首先对这个P(O|λ)计算:
这里等于对I求积分(这里因为是离散的 也就可以看成求和)
p ( O ∣ λ ) = ∑ I p ( I , O ∣ λ ) = ∑ I p ( O ∣ I , λ ) p ( I ∣ λ ) p(O|\lambda)=\sum\limits_{I}p(I,O|\lambda)=\sum\limits_{I}p(O|I,\lambda)p(I|\lambda) p(O∣λ)=I∑p(I,O∣λ)=I∑p(O∣I,λ)p(I∣λ)
这里最后一步是联合概率的乘法
*补充:联合概率的链式法则
这个概率图横向的箭头就代表aij(就是转移矩阵)
p ( I ∣ λ ) = p ( i 1 , i 2 , ⋯ , i t ∣ λ ) = p ( i t ∣ i 1 , i 2 , ⋯ , i t − 1 , λ ) p ( i 1 , i 2 , ⋯ , i t − 1 ∣ λ ) p(I|\lambda)=p(i_1,i_2,\cdots,i_t|\lambda)=p(i_t|i_1,i_2,\cdots,i_{t-1},\lambda)p(i_1,i_2,\cdots,i_{t-1}|\lambda) p(I∣λ)=p(i1,i2,⋯,it∣λ)=p(it∣i1,i2,⋯,it−1,λ)p(i1,i2,⋯,it−1∣λ)
利用齐次假设,然后后面继续递归写:
p ( i t ∣ i 1 , i 2 , ⋯ , i t − 1 , λ ) = p ( i t ∣ i t − 1 ) = a i t − 1 i t p(i_t|i_1,i_2,\cdots,i_{t-1},\lambda)=p(i_t|i_{t-1})=a_{i_{t-1}i_t} p(it∣i1,i2,⋯,it−1,λ)=p(it∣it−1)=ait−1it
最后等于:
即:
p ( I ∣ λ ) = π 1 ∏ t = 2 T a i t − 1 , i t p(I|\lambda)=\pi_1\prod\limits_{t=2}^Ta_{i_{t-1},i_t} p(I∣λ)=π1t=2∏Tait−1,it
【这上面π1应该是πi1哈 写错了】
同理 根据观测独立假设:
p ( O ∣ I , λ ) = ∏ t = 1 T b i t ( o t ) p(O|I,\lambda)=\prod\limits_{t=1}^Tb_{i_t}(o_t) p(O∣I,λ)=t=1∏Tbit(ot)
p ( O ∣ λ ) = ∑ I π i 1 ∏ t = 2 T a i t − 1 , i t ∏ t = 1 T b i t ( o t ) p(O|\lambda)=\sum\limits_{I}\pi_{i_1}\prod\limits_{t=2}^Ta_{i_{t-1},i_t}\prod\limits_{t=1}^Tb_{i_t}(o_t) p(O∣λ)=I∑πi1t=2∏Tait−1,itt=1∏Tbit(ot)
这里这个大I求和符号实际上是T个求和符号
这里这个大I求和是对 联合分布 求和得到 边缘分布

这里有T个求和符号,对每个i都有N种取值情况,所以这个式子是N^T的复杂度的
下面我们来介绍前向算法来计算这个式子:
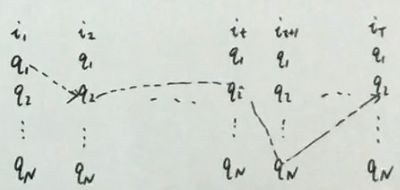
下面,记 α t ( i ) = p ( o 1 , o 2 , ⋯ , o t , i t = q i ∣ λ ) \alpha_t(i)=p(o_1,o_2,\cdots,o_t,i_t=q_i|\lambda) αt(i)=p(o1,o2,⋯,ot,it=qi∣λ),所以, α T ( i ) = p ( O , i T = q i ∣ λ ) \alpha_T(i)=p(O,i_T=q_i|\lambda) αT(i)=p(O,iT=qi∣λ)。我们看到:
p ( O ∣ λ ) = ∑ i = 1 N p ( O , i T = q i ∣ λ ) = ∑ i = 1 N α T ( i ) p(O|\lambda)=\sum\limits_{i=1}^Np(O,i_T=q_i|\lambda)=\sum\limits_{i=1}^N\alpha_T(i) p(O∣λ)=i=1∑Np(O,iT=qi∣λ)=i=1∑NαT(i)
α \alpha α也就是图中虚线这一块的联合概率(这里i代表第i个状态 t代表t时刻)
p ( O ∣ λ ) = ∑ i = 1 N p ( O , i T = q i ∣ λ ) p(O|\lambda)=\sum\limits_{i=1}^Np(O,i_T=q_i|\lambda) p(O∣λ)=i=1∑Np(O,iT=qi∣λ)这里就是联合分布对一个变量求积分求得边缘分布
下面来看 α \alpha α怎么方便计算(找到一个前向和后向关联的 迭代的公式)
所以看t+1
上面利用了齐次 Markov 假设得到了一个递推公式,这个算法叫做前向算法。
【这里还用了一个齐次markov假设化简】
对于evaluation问题,一般就用前向算法
3.evaluation问题——后向算法
前向算法通过定义了一个 α t ( i ) \alpha_{t}(i) αt(i)的一个式子来递推的
也就是图中蓝色的部分
后项算法在推导上比较麻烦
这里用了一个i从1到N计算边缘概率分布的公式
后面是条件概率的公式
发现后面那一项就是初始概率分布
*这里注意
初始概率分布可以看成这样的形式 因为I有N个取值
注意这里面的所有lambda都可以省略 因为lambda是已知的
这里发现P与 β 1 \beta_{1} β1有关
下面我们找通项中前后项的关系(递推关系式)
以上的总体推导过程为:
于是后向地得到了第一项。
这里 β \beta β在计算时是从后往前的,也就是从 β t \beta_{t} βt到 β t − 1 \beta_{t-1} βt−1…到 β 1 \beta_{1} β1
有了前向和后项算法,计算的复杂度大大降低了
4. learning问题——EM算法
我们知道:
λ = ( π , A , B ) \lambda=(\pi, A, B) λ=(π,A,B)
要求 π \pi π A B三个参数
首先我们想到用极大似然估计:
λ M L E = a r g m a x λ p ( O ∣ λ ) \lambda_{MLE}=\mathop{argmax}_\lambda p(O|\lambda) λMLE=argmaxλp(O∣λ)
使用EM算法(也叫Baum Welch算法),公式为:
θ t + 1 = a r g m a x θ ∫ z log p ( X , Z ∣ θ ) p ( Z ∣ X , θ t ) d z \theta^{t+1}=\mathop{argmax}_{\theta}\int_z\log p(X,Z|\theta)p(Z|X,\theta^t)dz θt+1=argmaxθ∫zlogp(X,Z∣θ)p(Z∣X,θt)dz
其中X是观测变量,Z是隐变量 θ是参数
X对应O
Z对应I
θ \theta θ对应 λ \lambda λ
故改写为:
λ t + 1 = a r g m a x λ ∑ I log p ( O , I ∣ λ ) p ( I ∣ O , λ t ) = a r g m a x λ ∑ I log p ( O , I ∣ λ ) p ( O , I ∣ λ t ) \lambda^{t+1}=\mathop{argmax}_\lambda\sum\limits_I\log p(O,I|\lambda)p(I|O,\lambda^t)\\ =\mathop{argmax}_\lambda\sum\limits_I\log p(O,I|\lambda)p(O,I|\lambda^t) λt+1=argmaxλI∑logp(O,I∣λ)p(I∣O,λt)=argmaxλI∑logp(O,I∣λ)p(O,I∣λt)
(积分号变连加号,因为是离散随机变量)
这里利用了 p ( O ∣ λ t ) p(O|\lambda^t) p(O∣λt) 和 λ \lambda λ 无关。
带入我们之前在Evaluation中推到过的式子把 P ( O , I ) P(O, I) P(O,I)代换掉:
p ( O ∣ λ ) = ∑ I π i 1 ∏ t = 2 T a i t − 1 , i t ∏ t = 1 T b i t ( o t ) p(O|\lambda)=\sum\limits_{I}\pi_{i_1}\prod\limits_{t=2}^Ta_{i_{t-1},i_t}\prod\limits_{t=1}^Tb_{i_t}(o_t) p(O∣λ)=I∑πi1t=2∏Tait−1,itt=1∏Tbit(ot)
( P ( O , I ) P(O, I) P(O,I)就是上面这个式子)
∑ I log p ( O , I ∣ λ ) p ( O , I ∣ λ t ) = ∑ I [ log π i 1 + ∑ t = 2 T log a i t − 1 , i t + ∑ t = 1 T log b i t ( o t ) ] p ( O , I ∣ λ t ) \sum\limits_I\log p(O,I|\lambda)p(O,I|\lambda^t)=\sum\limits_I[\log \pi_{i_1}+\sum\limits_{t=2}^T\log a_{i_{t-1},i_t}+\sum\limits_{t=1}^T\log b_{i_t}(o_t)]p(O,I|\lambda^t) I∑logp(O,I∣λ)p(O,I∣λt)=I∑[logπi1+t=2∑Tlogait−1,it+t=1∑Tlogbit(ot)]p(O,I∣λt)
(log把乘号变成了加号)
由于其他计算比较复杂,这里我们只以π的计算为例推导,A和B的就不推导了,理解思想即可
对于π:
log π i 1 + ∑ t = 2 T log a i t − 1 , i t + ∑ t = 1 T log b i t ( o t ) \log \pi_{i_1}+\sum\limits_{t=2}^T\log a_{i_{t-1},i_t}+\sum\limits_{t=1}^T\log b_{i_t}(o_t) logπi1+t=2∑Tlogait−1,it+t=1∑Tlogbit(ot)
因为只有第一项与π有关,所以后面两项可以消掉。
这里把大I写开了
发现:除了i1以外,从i2到iT 只有这个P里面有i2到iT
看做求 i 1 i_{1} i1的边缘分布,就可以消掉 i 2 i_{2} i2到 i T i_{T} iT,得到:
π t + 1 = a r g m a x π ∑ i 1 [ log π i 1 ⋅ p ( O , i 1 ∣ λ t ) ] \pi^{t+1}=\mathop{argmax}_\pi\sum\limits_{i_1}[\log \pi_{i_1}\cdot p(O,i_1|\lambda^t)] πt+1=argmaxπi1∑[logπi1⋅p(O,i1∣λt)]
把 i 1 i_{1} i1替换符号 求和写成i=1到N
这里的i是状态的下标 即
同时πi也已经有定义了(这些都是第一节讲的)
π i = P ( i 1 = q i ) \pi_{i}=P(i_{1}=q_{i}) πi=P(i1=qi)
因为π是概率分布,所以有约束: ∑ i π i = 1 \sum\limits_i\pi_i=1 i∑πi=1
有约束 所以我们用拉格朗日乘子法
定义Lagrange函数:
L ( π , η ) = ∑ i = 1 N log π i ⋅ p ( O , i 1 = q i ∣ λ t ) + η ( ∑ i = 1 N π i − 1 ) L(\pi,\eta)=\sum\limits_{i=1}^N\log \pi_i\cdot p(O,i_1=q_i|\lambda^t)+\eta(\sum\limits_{i=1}^N\pi_i-1) L(π,η)=i=1∑Nlogπi⋅p(O,i1=qi∣λt)+η(i=1∑Nπi−1)
后一项是把约束加进去的。
η是超参数
对πi求偏导
∂ L ∂ π i = 1 π i p ( O , i 1 = q i ∣ λ t ) + η = 0 \frac{\partial L}{\partial\pi_i}=\frac{1}{\pi_i}p(O,i_1=q_i|\lambda^t)+\eta=0 ∂πi∂L=πi1p(O,i1=qi∣λt)+η=0
即:
P ( O , i 1 = q i ∣ λ t ) + π i η = 0 P(O, i_{1}=q_{i}|\lambda^t) + \pi_{i}\eta = 0 P(O,i1=qi∣λt)+πiη=0
利用条件:
s . t . ∑ i = 1 N π i = 1 \mathrm{ s.t. }\sum\limits_{i=1}^N\pi_i=1 s.t.i=1∑Nπi=1
式子两边同时求和(i从1到N):
P ( O ∣ λ t ) + η = 0 P(O|\lambda^t)+\eta=0 P(O∣λt)+η=0
所以:
η = − p ( O ∣ λ t ) \eta=-p(O|\lambda^t) η=−p(O∣λt)
再把 η \eta η带入式子中,解得 π i \pi_{i} πi:
π i t + 1 = p ( O , i 1 = q i ∣ λ t ) p ( O ∣ λ t ) \pi_i^{t+1}=\frac{p(O,i_1=q_i|\lambda^t)}{p(O|\lambda^t)} πit+1=p(O∣λt)p(O,i1=qi∣λt)
A和B就不做过多推导了
5.decoding问题——Viterbi算法
Decoding 问题表述为:
I = a r g m a x I p ( I ∣ O , λ ) I=\mathop{argmax}\limits_{I}p(I|O,\lambda) I=Iargmaxp(I∣O,λ)
我们需要找到一个序列,其概率最大,这个序列就是在参数空间中的一个路径,可以采用动态规划的思想。
很多人吧decoding叫做预测问题
但个人偏向于叫做解码问题
因为预测问题是:
给定T时刻,求T+1的后验概率
decoding也是求后验概率,但是求的是完整i1到it的序列 所以用decoding这个术语更贴切
我们给定一个观测序列I,求得一个最有可能出现的I(隐状态)序列
由于这里Q是I的值域,那么对于每一个i 都有q1…qN个值的选择
假如说随便组合,一共有T个i的话,就是N^T 指数级种组合方式
我们就是要从N^T个序列中挑出一个序列,使得后验概率最大。
这实际是一个动态规划问题
比如我们的序列的取值是这样这样取的
动态规划问题就是比如:路径规划 比如有N个车站,先到哪个车站 怎么走怎么走 找一个最短路径。。。只不过这里是找一个最大概率
q1->q2对应 P ( q 2 ∣ q 1 ) P(q2|q1) P(q2∣q1)
我们把概率类比成距离
比如距离=1/概率
意思就是概率越大距离越短 路径就最优
定义:
δ t ( j ) = max i 1 , ⋯ , i t − 1 p ( o 1 , ⋯ , o t , i 1 , ⋯ , i t − 1 , i t = q i ) \delta_{t}(j)=\max\limits_{i_1,\cdots,i_{t-1}}p(o_1,\cdots,o_t,i_1,\cdots,i_{t-1},i_t=q_i) δt(j)=i1,⋯,it−1maxp(o1,⋯,ot,i1,⋯,it−1,it=qi)
o1…ot已知
这个式子的意思就是到qi这个点的最大概率的概率值
下面找递推式:
δ t + 1 ( j ) = max i 1 , i 2 , . . . , i n P ( O 1 , O 2 , . . . , O t , O t + 1 , i 1 , i 2 , . . . , i t , i t + 1 = q j ) \delta_{t+1}(j)=\max\limits_{i_{1}, i_{2}, ... ,i_{n}}P(O_{1}, O_{2}, ..., O_{t}, O_{t+1}, i_{1}, i_{2}, ..., i_{t}, i_{t+1}=q_{j}) δt+1(j)=i1,i2,...,inmaxP(O1,O2,...,Ot,Ot+1,i1,i2,...,it,it+1=qj)
从上图看,就是前面的N种情况转移到qj的概率中的最大值
最后得出:
δ t ( j ) = max i 1 , ⋯ , i t − 1 p ( o 1 , ⋯ , o t , i 1 , ⋯ , i t − 1 , i t = q i ) \delta_{t}(j)=\max\limits_{i_1,\cdots,i_{t-1}}p(o_1,\cdots,o_t,i_1,\cdots,i_{t-1},i_t=q_i) δt(j)=i1,⋯,it−1maxp(o1,⋯,ot,i1,⋯,it−1,it=qi)
这个式子就是从上一步到下一步的概率再求最大值。记这个路径为:
ψ t + 1 ( j ) = a r g m a x 1 ≤ i ≤ N δ t ( i ) a i j ψ t + 1 ( j ) = a r g m a x 1 ≤ i ≤ N δ t ( i ) a i j \psi_{t+1}(j)=\mathop{argmax}\limits_{1\le i\le N}\delta_t(i)a_{ij}\psi_{t+1}(j)=\mathop{argmax}\limits_{1\le i\le N}\delta_t(i)a_{ij} ψt+1(j)=1≤i≤Nargmaxδt(i)aijψt+1(j)=1≤i≤Nargmaxδt(i)aij
6.小结:
HMM 是一种动态模型,是由混合树形模型和时序结合起来的一种模型(类似 GMM + Time)。对于类似 HMM 的这种状态空间模型,普遍的除了学习任务(采用 EM )外,还有推断任务,推断任务包括:
-
译码 Decoding: p ( z 1 , z 2 , ⋯ , z t ∣ x 1 , x 2 , ⋯ , x t ) p(z_1,z_2,\cdots,z_t|x_1,x_2,\cdots,x_t) p(z1,z2,⋯,zt∣x1,x2,⋯,xt)
-
似然概率: p ( X ∣ θ ) p(X|\theta) p(X∣θ)
-
滤波:$ p(z_t|x_1,\cdots,x_t)$,Online
p ( z t ∣ x 1 : t ) = p ( x 1 : t , z t ) p ( x 1 : t ) = C α t ( z t ) p(z_t|x_{1:t})=\frac{p(x_{1:t},z_t)}{p(x_{1:t})}=C\alpha_t(z_t) p(zt∣x1:t)=p(x1:t)p(x1:t,zt)=Cαt(zt) -
平滑: p ( z t ∣ x 1 , ⋯ , x T ) p(z_t|x_1,\cdots,x_T) p(zt∣x1,⋯,xT),Offline
p ( z t ∣ x 1 : T ) = p ( x 1 : T , z t ) p ( x 1 : T ) = α t ( z t ) p ( x t + 1 : T ∣ x 1 : t , z t ) p ( x 1 : T ) p(z_t|x_{1:T})=\frac{p(x_{1:T},z_t)}{p(x_{1:T})}=\frac{\alpha_t(z_t)p(x_{t+1:T}|x_{1:t},z_t)}{p(x_{1:T})} p(zt∣x1:T)=p(x1:T)p(x1:T,zt)=p(x1:T)αt(zt)p(xt+1:T∣x1:t,zt)
根据概率图的条件独立性,有:
p ( z t ∣ x 1 : T ) = α t ( z t ) p ( x t + 1 : T ∣ z t ) p ( x 1 : T ) = C α t ( z t ) β t ( z t ) p(z_t|x_{1:T})=\frac{\alpha_t(z_t)p(x_{t+1:T}|z_t)}{p(x_{1:T})}=C\alpha_t(z_t)\beta_t(z_t) p(zt∣x1:T)=p(x1:T)αt(zt)p(xt+1:T∣zt)=Cαt(zt)βt(zt)
这个算法叫做前向后向算法。 -
预测: p ( z t + 1 , z t + 2 ∣ x 1 , ⋯ , x t ) , p ( x t + 1 , x t + 2 ∣ x 1 , ⋯ , x t ) p(z_{t+1},z_{t+2}|x_1,\cdots,x_t),p(x_{t+1},x_{t+2}|x_1,\cdots,x_t) p(zt+1,zt+2∣x1,⋯,xt),p(xt+1,xt+2∣x1,⋯,xt)
p ( z t + 1 ∣ x 1 : t ) = ∑ z t p ( z t + 1 , z t ∣ x 1 : t ) = ∑ z t p ( z t + 1 ∣ z t ) p ( z t ∣ x 1 : t ) p(z_{t+1}|x_{1:t})=\sum_{z_t}p(z_{t+1},z_t|x_{1:t})=\sum\limits_{z_t}p(z_{t+1}|z_t)p(z_t|x_{1:t}) p(zt+1∣x1:t)=zt∑p(zt+1,zt∣x1:t)=zt∑p(zt+1∣zt)p(zt∣x1:t)p ( x t + 1 ∣ x 1 : t ) = ∑ z t + 1 p ( x t + 1 , z t + 1 ∣ x 1 : t ) = ∑ z t + 1 p ( x t + 1 ∣ z t + 1 ) p ( z t + 1 ∣ x 1 : t ) p(x_{t+1}|x_{1:t})=\sum\limits_{z_{t+1}}p(x_{t+1},z_{t+1}|x_{1:t})=\sum\limits_{z_{t+1}}p(x_{t+1}|z_{t+1})p(z_{t+1}|x_{1:t}) p(xt+1∣x1:t)=zt+1∑p(xt+1,zt+1∣x1:t)=zt+1∑p(xt+1∣zt+1)p(zt+1∣x1:t)