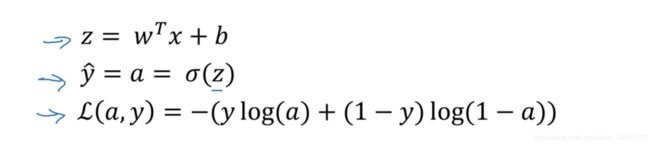吴恩达深度学习 C1_W2
C1_W2
接下来我们开始第二周(?)的学习
二分分类
那首先什么叫做二分分类呢？我个人的理解就是一个结果分为是与否的问题。
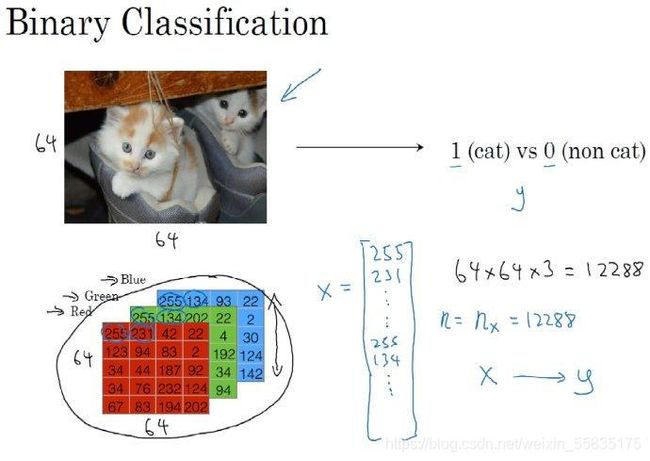
例如：给定一张图片，让机器判断这张图片中是否有猫的存在。是则输出1，不是则输出0，然后用y来表示输出的结果标签。
计算机保存一张图片，要保存三个独立矩阵分别代表图片红绿蓝的三个颜色通道。如果输入的图片是6464像素的，就会有三个6464的矩阵，矩阵中元素的值分别代表对于像素点三种不同像素的亮度。
为了方便计算，就把红绿蓝三个矩阵的元素从左到右从上到下依次列出来，合并成一个长度为36464的特征向量x，nx=12288表示这个特征向量的维度。
在二分分类中的问题中，我们的目标是训练出一个分类器（classifier）它以特征向量x作为输入预测出结果y是0还是1，也就是预测出图片中是否含有猫。
接下来老师列举了一些会常用到的符号：
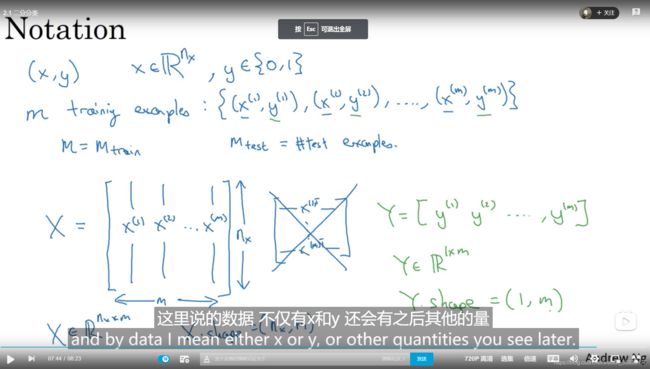
第一行的(x,y)表示一个单独的样本，x是一个nx维度的特征向量，y为0或者1。一个训练集(training example)由m个样本组成，后面(x,y)对的上标i即表示为第i个样本中的x和y，m=m_train表示样本的长度。
接下来我们将m个列向量xi(这里的i为上标)合并成一个nxm的矩阵X，然后将y1，y2······ym组成一个1m的行向量Y，数据的处理到这里就ok了。
logistic 回归
已知输入的x，我们需要一个算法，去得到一个预测值y ^（y hat）表示对y的预测。y可能为1，可能为0，于是y ^为0-1的一个值，表示y可能为1的概率。
例如：x为一张图片，y ^表示这个图片里有猫的概率。
logistic回归中含有两个参数W,b，W为一个nx维度的向量，b为一个实数。
这样子处理有很大的问题，因为我们需要得到的y ^为0-1的一个值，而线性函数的值域显然不是0-1。于是在这个算式外面套一个sigmoid函数：
这个sigmoid上一个章节就简单的提到了一下：
(右边的为函数式)
这个函数能够很好的将R值域上的数值x转化为0-1的数值，其中x越大越接近于1，x越小越接近于0，x越大和越小的时候函数值的变化率都比较小接近于0。
老师后面还介绍了一些对W和b的其他表达方式，不过老师不会在这门课中进行使用，于是不多作赘述(我懒)。
logistic 回归损失函数
首先是上一节课提到的内容：
接下来老师介绍了损失函数，也被称为误差函数：
这是我们处理一般数据的做法，其实就是方差。但是这个做法在梯度下降法中适用性不高，所以一般用下面的函数：
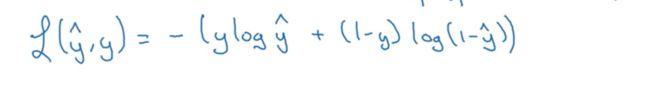
可能有点看不清，我第一看的时候，就是把括号看成了log：
当y=1时，这个函数为-log(y ^)，此时y ^越接近于1，误差函数的值越小，相反的y越接近于0，误差函数值越大。
y=0时，函数为-log(1-y ^)，同理。
损失函数衡量单个训练样本的表现。定义一个成本函数(m个损失函数的算数平均和)去找到合适的W和b(让成本函数的值较小)：
成本函数是通过衡量整个训练集来测试W和b的。
梯度下降法
前几个章节学习的内容：
成本函数为有多个局部最优的凸函数，呈这样的一个图像，我们的目标就是找到合适的W和b是的成本函数最小：
那我们怎么做呢？首先取一个边界点(W,b)，将边界点的按照最陡的方向往下走，一步一步收敛到最终的结果：
接下来老师举了一个比较直观的平面例子：
那个α表示学习率，我个人觉得取的微小的变化量，这个仔细看，感觉就是高数书上用切线法去逼迫方程根(函数极值的问题本质上也是导数求解)。
需要注意的是上面的公式，在函数左边和右边的两个不同的变化趋势的部分的效果是相同的，在左边时，变化率小于0，会使得W的值越来越大，找到中间的W。(这里的变化率是对W和b分别求的偏导)
总的来说，就是介绍了用切线法去得到导数为0，即函数值为极小值的过程。
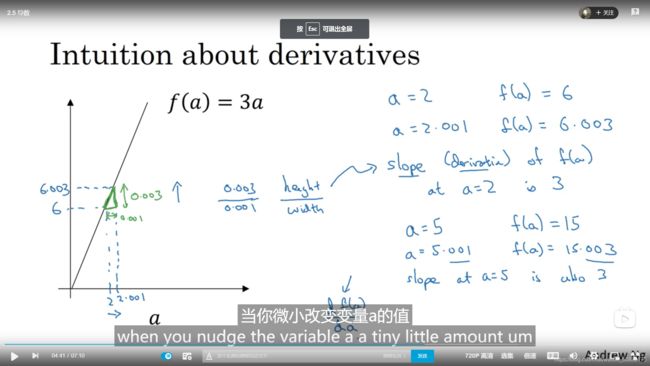
导数
你甚至能够在深度学习的课中学到高数的知识hhhh
就是简单介绍了导数的定义，以x作为一个点，在Δx(x的变化量)趋近于0，Δy/Δx即为在x这个点的变化率，即导数。
更多导数的例子
依旧是在讲高数的内容hhhhh
感觉只要不是高数挂科的人这两章的内容都不是很必要去听。
计算图
我看到这个标题的时候一惊，还以为是图论里的那个计算图，事实上就是我们最近刚好学到的多元复合函数求导：
按照蓝色方向即为计算方向，红色即为反向的求导方向(反向传输操作)。
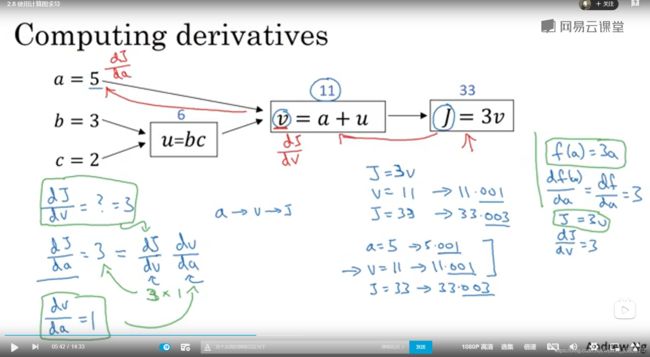
使用计算图求导
依旧是之前的一个例子：
由于之前的章节，我们了解到y关于x的导数，即代表x增加了一个微小的变化量，y产生的变化量除以这个x的变化量得到的变化率。
也就是说这里J关于v的导数，即为v的变化量对于J的影响。
那么我们要求关于J关于a的导数呢？首先我们发现a是v函数的一个变量，v关于a的导数d1表示a的变化量对v的影响。J关于v的导数d2则表示v的变化率对于J的影响。我们将d1*d2即为a对v的影响导致v变化对J产生了影响，可以理解为a对J产生的影响，即是J关于a的导数，这就是复合函数求导的链式法则。
为啥叫链式呢？因为链表的存储是根据值首尾的联系存储的，而不是一般地直接连续存储，我个人觉得多元复合函数的存储方式比较像一个树，v,u即为这个树的结点，像这里J对a求导实际就是在一个树的数据结构中通过深度遍历或者广度遍历(我个人觉得深度遍历更加容易去理解)去找到a这个结点。
以上就是我对于多元复合函数求导的链式法则，以及计算机模拟这个问题，个人的一些理解。
logistic回归中的梯度下降法
先回顾之前的公式：
接下来我们开始求导，首先是L关于a的导数：
注意是偏导所以y是看作常数的。
再进一步进行求导，得到L关于z的导数为a-y：
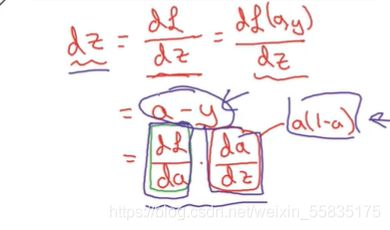
dW1，dW2和dz的导数分别为：
m个样本的梯度下降
我们在上一章节得到了单个样本的损失函数的参数W和b关于z的导数，接下来我们需要考虑整个训练集的成本函数：
求个算术平均数。
伪代码实现梯度下降：
这个其实挺简单的hhhh
向量化
对于之前的伪代码实现梯度下降法，我么需要使用for循环。那什么叫做向量化，就是通过使用python中numpy库的一些工具，避免循环直接进行操作。
上面的代码中，前两行表示在a和b中分别定义了1000000个随机数的数组，第一种方法是用一个dot方法，一对一的进行点乘(dot本身是一个处理矩阵的方法哦)，第二种方法是用for循环的方式模拟乘的过程。
我们可以发现，消耗的时间相差了400倍之多(至于为什么，因为numpy是用C写的，而对于python语言，由于python是解释性语言，也就是说在循环的过程中，还要多做很多对字符串的处理，判断等操作，这样会大大增大消耗的时间)
向量化的更多例子
这一章没有什么思维难度，就是介绍了一些工具去代替for循环：
下面是对m个样例梯度下降向量化的优化：
其实主要就是一个赋值为0，和一个加法的操作。由于我对numpy没有一个充分的了解(毕竟写C,C++比较多，编译型语言这种问题就比较少)，就不在这里献丑了。
向量化 logistic回归
我们之前已经提到过，将m个x列向量堆叠成一个nx*m的矩阵X。这节课的内容就在于通过矩阵X将logistic回归给向量化：
zi=w.Txi+b。这里的T表示矩阵转置的意思，w的转置即为一个nx维度的行向量，w乘以xi我们可以得到一个值(11的矩阵)，当我们将m个x全部堆叠起来，可以得到1*m的一个行向量，行向量的每一个元素加上b就可以得到 [z1,z2,z3·····zm]
最下面就是通过一句代码得到我们的结果，前半句比较好理解，W的转置矩阵乘以X，可b不是一个实数么，事实上python里面有一个广播的概念可以将b变为一个1*m的行向量 [b,b,b,b····]进行相加。
这样就完成了logistic回归的向量化。
向量化 logistic回归的梯度输出
接下来我们要向量化logistic回归梯度下降的运算过程：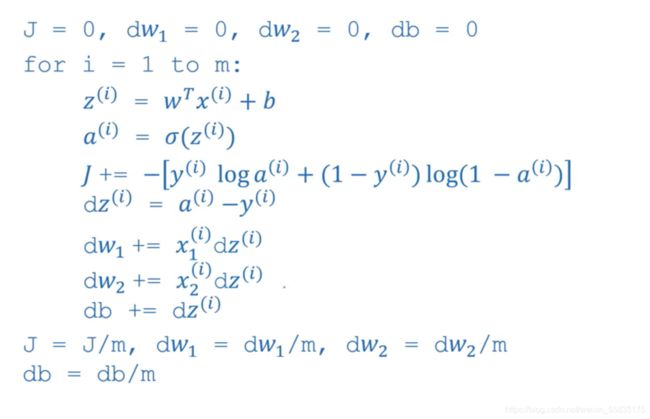
上面是原本的代码，接下来进行向量化：
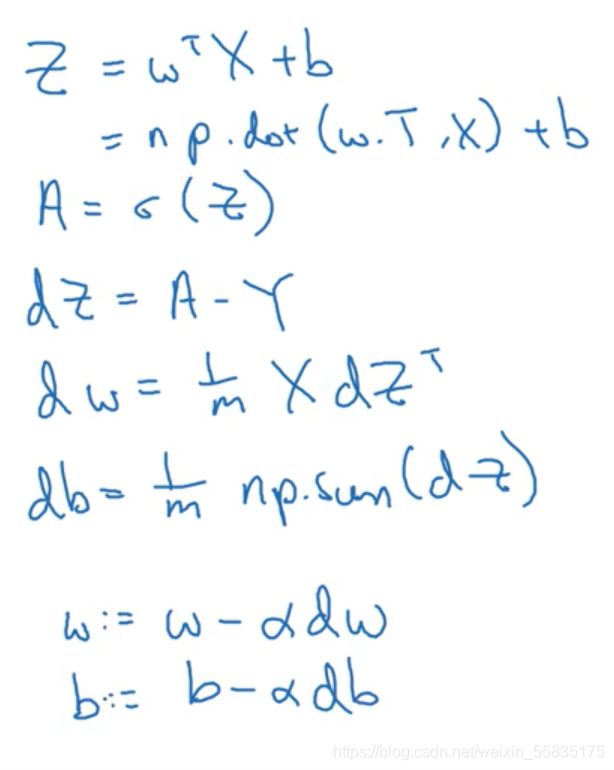
第一步是将m个x向量进行堆叠得到堆叠后的z(b依旧需要被广播)，m次的a-y转化为A-Y(堆叠为矩阵)，对于m个z的求和，这里直接使用了sum方法进行求和。
Python中的广播
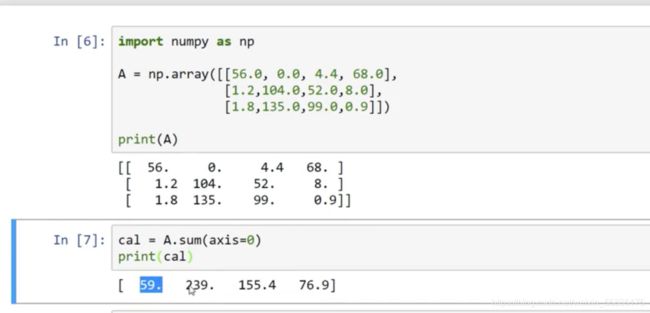
老师举了一个例子：
这里是一个小型的数据库，我们需要得到的是每种营养在一种食品整个营养中的占比，例如apples中carb的占比为56.0/(56.0+1.2+1.8)*100%
代码如下：
axis=0表示按照列从头开始求和。
直接相除得到了结果。
事实上按照正常的想法可能会觉得很奇怪，因为这个怎么能相除呢？事实上python通过广播(broadcasting)的功能将14的这个矩阵拉长为了34，将原矩阵复制了三遍添加上，然后在每一个元素进行相除。
这时我们想到之前矩阵加上实数b的操作，本质是一样的，通过广播的功能将b复制m遍，得到一个1*m的向量。
三个例子：
关于python numpy 向量化的说明
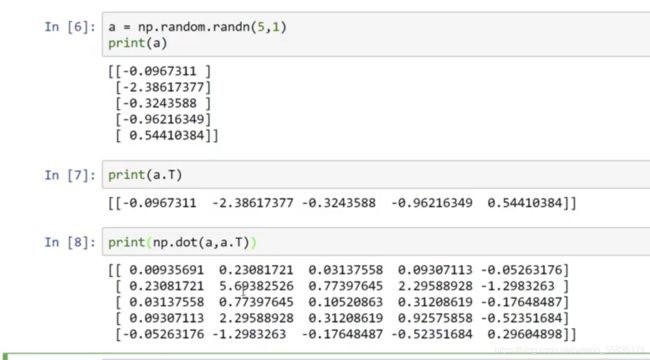
主要是介绍了一个numpy的一些功能和小bug：
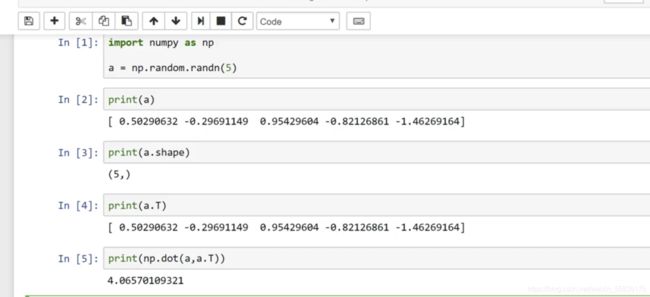
这里我们可以发现，通过这种方式定义的a矩阵的列长度是一个行长度是一个不确定的值，因此我们无法对a矩阵进行转置和点乘。
这样子定义，就可以得到我们想要的结果：
得到的结论：
关于jupyter notebook
这个实在没什么好说的，因为anaconda是自带jupyter notebook的，可以用来在交互式的环境下，测试一些简短的代码。(注意是交互式)