波兰表达式和逆波兰表达式

波兰表达式和逆波兰表达式

今天zxy的实验内容是关于逆波兰表达式的计算，刚好最近在做关于数据结构的习题，于是想着对波兰表达式和逆波兰表达式的转化和运算分别进行一个学习，于是写了这篇博客(有错的地方欢迎大家指出。)

常见的运算表达式，我们一般称为中缀表达式，例如：

5 + ( 6 - 4 / 2 ) * 3

---

波兰表达式

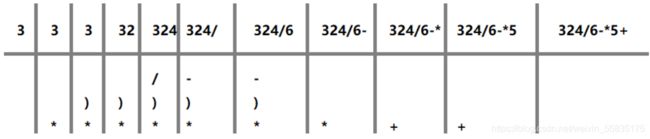
波兰表达式子我们也称作前缀表达式，就是对中缀表达式进行如下的操作：

首先建立两个栈，一个栈s1用于落实我们最后得到的前缀表达式，一个栈s2用于暂存表达式中的运算符。

对中缀表达式从右向左进行遍历：

如果是数字：则直接压入栈s1。

如果是括号：分为两种情况，如果是右括号，则直接压入栈s2；如果是左括号，我们将栈s2中的运算符依次弹栈到栈s1，直到s1栈顶元素为右括号，将右括号弹栈，结束。

如果是其他运算符：将此时s2栈顶运算符的优先级与该运算符进行比较。如果s2栈顶操作符优先级大于该运算符优先级，则s2弹栈加入到栈s1中，直到s2栈顶操作符优先度小于等于该运算符优先级，将当前运算符压入栈s2中。

遍历完整个中缀表达式后，检测栈s2是否为空。如果不为空，则将s2中的运算符依次弹栈，压入栈s1中。

最后将栈s1中的元素依次弹出(反序输出)，得到的即是前缀表达式。

模拟过程：

代码实现：

#include
#include
#include
#include
using namespace std;
stack<char>s1,s2;//s1表示存放波兰表达式的栈,s2用于暂存运算符 
map<char,int>ch_level;//用于建立运算符到优先级的映射 
string s;
void BL(int x){
     //转化递归函数 
	if (x<0) return;//递归结束 
	if (isdigit(s[x])) {
     s1.push(s[x]); BL(x-1);}//如果是数字直接进栈s1 
	else if (s[x]==')'){
     s2.push(s[x]); BL(x-1);}//右括号直接进栈s2
	//遍历到左括号,将栈s2中右括号之上的运算符全部压入栈s1中
	//需要注意的是,由于我们可以确定此时栈中必然存在一个右括号,所以在while中不用判断栈是否为空 
	else if (s[x]=='('){
     while (s2.top()!=')'){
     s1.push(s2.top()); s2.pop();} s2.pop();BL(x-1);}
	else {
     //如果是其他运算符,就对优先级进行比较,这里需要判断栈是否为空 
		while (!s2.empty()&&ch_level[s[x]]>ch_level[s2.top()]){
     s1.push(s2.top()); s2.pop();}
		s2.push(s[x]); BL(x-1); 
	}
}
int main(){
     
	ch_level['/']=1;ch_level['*']=1;ch_level['%']=1;//这三个的优先级比+和-高 
	ch_level['+']=2;ch_level['-']=2;ch_level['(']=3;ch_level[')']=3;
	//括号的优先级确实应该是最高的,但是我在观察流程的时候,发现括号是不参与运算符的比较的
	//所以我默认括号的运算符等级最低 
	cin>>s; BL(s.size()-1);
	while(!s2.empty()){
     s1.push(s2.top());s2.pop();}//将栈s2中剩余的元素依次压入s1中 
	while (!s1.empty()){
     cout<<s1.top()<<" ";s1.pop();}//输出结果,因为是栈所以自动进行了翻转
	return 0; 
}

---

波兰表达式计算

对前缀表达式从后向前进行遍历，建立一个栈s，如果是数字，则将其直接压入栈s。

如果遍历到的是运算符，则从栈s中弹出两个数按照运算符的规则进行运算，并将计算结果压入栈s中。

合法的前缀表达式遍历结束后，栈s中剩余的元素只剩下一个，就是我们需要的结果。

代码实现：

#include
#include
#include
using namespace std;
int main(){
     
	string s; cin>>s;
	stack<int>ans; bool flag=true;//flag表示这个式子是否合法 
	for (int i=s.size()-1;i>=0&&flag;i--){
      
		if (isdigit(s[i])) ans.push((int)s[i]-48);//如果是数字则直接进栈 
		else {
     //这里首先需要判断一下栈的长度是否足够弹出两个数,如果不足够说明表达式不合法 
			if (ans.size()<2) {
     flag=false; break;}
			int a=ans.top(); ans.pop();
			int b=ans.top(); ans.pop();
			switch (s[i]){
     //不同运算符的不同运算法则 
				case '+':ans.push(a+b);break;
				case '-':ans.push(a-b);break;
				case '*':ans.push(a*b);break;
				case '/':{
     //除法和余数需要判断除数是否为0 
					if (!b) flag=false; else ans.push(a/b); break;
				}
				case '%':{
     
					if (!b) flag=false; else ans.push(a%b); break;
				}
			}
		}
	}
	if (ans.size()!=1) flag=false;//判断栈中的值是否为1 
	if (flag) cout<<ans.top(); else cout<<"非法表达式";
	return 0; 
} 

我们将两个代码结合起来就可以得到一个普通算式的计算结果。

---

逆波兰表达式

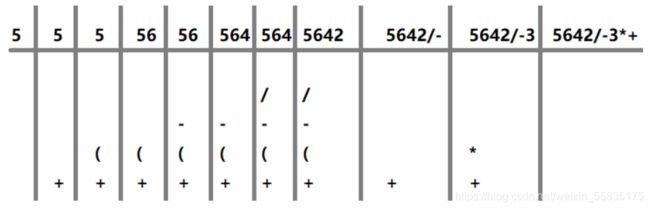
逆波兰表达式也称后缀表达式，就是对中缀表达式进行如下操作：

对中缀表达式从左向右进行遍历：

如果是数字：则直接压入栈s1。

如果是括号：分为两种情况，如果是左括号，则直接压入栈s2；如果是右括号，我们将栈s2中的运算符依次弹栈到栈s1，直到s1栈顶元素为右括号，将右括号弹栈，结束。

如果是其他运算符：将此时s2栈顶运算符的优先级与该运算符进行比较。如果大于等于该运算符优先级s2栈顶操作符优先级，则s2弹栈加入到栈s1中，直到s2栈顶操作符优先度小于该运算符优先级，将当前运算符压入栈s2中。

遍历完整个中缀表达式后，检测栈s2是否为空。如果不为空，则将s2中的运算符依次弹栈，压入栈s1中。

最后将栈s1中的元素(正序输出)，得到的即是后缀表达式。

模拟流程：

可以发现的是，后缀表达式的转化和前缀表示式只有一些细微的差别。可以说是反过来了，所以代码只需要进行很小的修改就可以了：

#include
#include
#include
#include
using namespace std;
stack<char>s1,s2;//s1表示存放逆波兰表达式的栈,s2用于暂存运算符 
map<char,int>ch_level;//用于建立运算符到优先级的映射 
string s;
void NBL(int x){
     //转化递归函数 
	if (x==s.size()) return;//递归结束 
	if (isdigit(s[x])) {
     s1.push(s[x]); NBL(x+1);}//如果是数字直接进栈s1 
	else if (s[x]=='('){
     s2.push(s[x]); NBL(x+1);}//左括号直接进栈s2
	//遍历到右括号,将栈s2中右括号之上的运算符全部压入栈s1中
	//需要注意的是,由于我们可以确定此时栈中必然存在一个左括号,所以在while中不用判断栈是否为空 
	else if (s[x]==')'){
     while (s2.top()!='('){
     s1.push(s2.top()); s2.pop();} s2.pop();NBL(x+1);}
	else {
     //如果是其他运算符,就对优先级进行比较,这里需要判断栈是否为空 
		while (!s2.empty()&&ch_level[s[x]]>=ch_level[s2.top()]){
     s1.push(s2.top()); s2.pop();}
		s2.push(s[x]); NBL(x+1); 
	}
}
int main(){
     
	ch_level['/']=1;ch_level['*']=1;ch_level['%']=1;//这三个的优先级比+和-高 
	ch_level['+']=2;ch_level['-']=2;ch_level['(']=3;ch_level[')']=3;
	//括号的优先级确实应该是最高的,但是我在观察流程的时候,发现括号是不参与运算符的比较的
	//所以我默认括号的运算符等级最低 
	cin>>s; NBL(0);
	char ans_c[100]; int num=0;
	while(!s2.empty()){
     s1.push(s2.top());s2.pop();}//将栈s2中剩余的元素依次压入s1中
	while (!s1.empty()){
     ans_c[num]=s1.top();s1.pop();num++;}
	for (int i=num-1;i>=0;i--) cout<<ans_c[i]; //正序输出,但是对于栈而言是反序 
	return 0; 
}

---

逆波兰表达式的计算

对后缀表达式从前向后进行遍历，建立一个栈s，如果是数字，则将其直接压入栈s。

如果遍历到的是运算符，则从栈s中弹出两个数按照运算符的规则进行运算，并将计算结果压入栈s中。

合法的后缀表达式遍历结束后，栈s中剩余的元素只剩下一个，就是我们需要的结果。

和波兰表达式也是非常类似的，这里我将转化和计算的两个代码结合了起来：

#include
#include
#include
#include
using namespace std;
stack<char>s1,s2;//s1表示存放逆波兰表达式的栈,s2用于暂存运算符 
map<char,int>ch_level;//用于建立运算符到优先级的映射 
string s;
void NBL(int x){
     //转化递归函数 
	if (x==s.size()) return;//递归结束 
	if (isdigit(s[x])) {
     s1.push(s[x]); NBL(x+1);}//如果是数字直接进栈s1 
	else if (s[x]=='('){
     s2.push(s[x]); NBL(x+1);}//左括号直接进栈s2
	//遍历到右括号,将栈s2中右括号之上的运算符全部压入栈s1中
	//需要注意的是,由于我们可以确定此时栈中必然存在一个左括号,所以在while中不用判断栈是否为空 
	else if (s[x]==')'){
     while (s2.top()!='('){
     s1.push(s2.top()); s2.pop();} s2.pop();NBL(x+1);}
	else {
     //如果是其他运算符,就对优先级进行比较,这里需要判断栈是否为空 
		while (!s2.empty()&&ch_level[s[x]]>=ch_level[s2.top()]){
     s1.push(s2.top()); s2.pop();}
		s2.push(s[x]); NBL(x+1); 
	}
}
int main(){
     
	ch_level['/']=1;ch_level['*']=1;ch_level['%']=1;//这三个的优先级比+和-高 
	ch_level['+']=2;ch_level['-']=2;ch_level['(']=3;ch_level[')']=3;
	//括号的优先级确实应该是最高的,但是我在观察流程的时候,发现括号是不参与运算符的比较的
	//所以我默认括号的运算符等级最低 
	cin>>s; NBL(0);
	char ans_c[100]; int num=0;
	while(!s2.empty()){
     s1.push(s2.top());s2.pop();}//将栈s2中剩余的元素依次压入s1中
	while (!s1.empty()){
     ans_c[num]=s1.top();s1.pop();num++;}
	stack<int>ans; bool flag=true; 
	for (int i=num-1;i>=0&&flag;i--){
     
		cout<<ans_c[i];
		if (isdigit(ans_c[i])) ans.push((int)ans_c[i]-48);//如果是数字则直接进栈
		else {
     //这里首先需要判断一下栈的长度是否足够弹出两个数,如果不足够说明表达式不合法 
			if (ans.size()<2) {
     flag=false; break;}
			int a=ans.top(); ans.pop();
			int b=ans.top(); ans.pop();
			switch (ans_c[i]){
     //不同运算符的不同运算法则 
				case '+':ans.push(a+b);break;
				case '-':ans.push(b-a);break;
				case '*':ans.push(a*b);break;
				case '/':{
     //除法和余数需要判断除数是否为0 
					if (!a) flag=false; else ans.push(b/a); break;
				}
				case '%':{
     
					if (!a) flag=false; else ans.push(b%a); break;
				}
			}
		}
	}
	cout<<endl;
	if (ans.size()!=1) flag=false;//判断栈中的值是否为1 
	if (flag) cout<<ans.top(); else cout<<"非法表达式";
	return 0; 
}

结果看上去还是不错的：

---

查了一些资料发现可以将中缀表达式像以下的方法解析成一个树：

中缀表达式得名于它是由相应的语法树的中序遍历的结果得到的。上面的二叉树中序遍历的结果就是A+B*(C-D)-E*F。

前缀表达式是由相应的语法树的前序遍历的结果得到的。上图的前缀表达式为- + A * B - C D * E F

后缀表达式又叫做逆波兰式。它是由相应的语法树的后序遍历的结果得到的。上图的后缀表达式为：A B C D - * + E F * -

也就是说理论上可以通过树对这个问题进行处理，但是具体怎么实现我还没有想明白，有想法的欢迎大家和我交流(我知道没人会来，所以我还是去问老师)。