第十二届蓝桥杯模拟赛（第四期）题解 Python版

引言

虽然之前也写过一些力扣题解，但都比较简单，而且语言描述得比较不好吧，基本算是一个记录性质的博客。博主参加过第十二届蓝桥杯模拟赛的第二期、第三期和本次第四期，第一期还不知道有这个模拟赛所以没参加，鉴于第四期个人感觉难度较低，所以尝试做一下题解！有问题欢迎评论区交流！

由于本人参加的是Python组，所以很多地方的代码可能会带有Python风格

填空题1

非常基础的一道题，给定一个固定的ASCII码，求该ASCII码对应的字符是什么。

这里要掌握的是Python字符和ASCII码之间转换的函数
1、字符转ASCII码：ord()
2、ASCII码转字符：chr()
本题直接用chr()函数将 80 这个ASCII码转换即可

print(chr(80))
# 输出 P

填空题2

第二题涉及的是质数、质因数、互质之类的知识，个人感觉算是蓝桥杯经常考察的一个点吧。

解决本题，首先要掌握如何确定一个数是否是质数，然后从1900遍历到2020，依次判断每一个数是否是质数。

由于本题给出的范围比较大（大于等于5了），所以我写的判断质数省略了小于5的部分，也不影响解题。

import math
# 判断一个数是否为质数（根据本题精简版）
def is_prime(n):
    if n % 6 == 1 or n % 6 == 5:
        for i in range(2, int(math.sqrt(n)+1)):
            if n % i == 0:
                return False
        return True
    else:
        return False

这个判断质数的原理是刷力扣刷到过的，具体哪个题肯定是想不起来了，我在这里大概描述一下：
任意大于等于5的数，如果被 6 除的余数是 0、2、3、4，那个这个数一定不是质数，为什么呢？

以被6除，余数为2的数为例，这个数我们可以表示成 6n + 2，而 6n + 2 = 2 * (3n + 1)，该数一定是2的倍数，故确定不是质数。

类似的，被 6 除余数为0的数不用说（6的倍数呗），余数为3的数是 6n + 3 = 3 * (2n + 1)——3的倍数；余数为4的数是6n + 4 = 2 * (3n + 2)，也是2的倍数。

所以我们可以把判断的目标放在那些除6余数为 1 和 5 的数上，这些数“有可能”为质数，不绝对，因此需要从2遍历到根号n（判断质数标准套路），虽然最后判断质数的方法很标准很老套，但我们每6个数可以淘汰掉4个不可能为质数的数，因此效率还是比较高的。

好了，有了判断质数的方法，那我们就依次判断题设范围内的每一个数，统计返回True的数量即可。

print(len(list(filter(is_prime, range(1900, 2021)))))
# 输出16

这里涉及Python过滤器filter()的使用，由于判断质数的函数返回的是布尔值，所以自然想到了直接用过滤器来写。
要注意的就是过滤器返回的是一个过滤器对象，不能直接判断长度，要先转换成列表再判断长度。

觉得过滤器麻烦的也可以这么写，比较朴素

res = 0
for num in range(1900, 2021):
    res += 1 if is_prime(num) else 0
print(res)
# 同样输出16

填空题3

二叉树，给条件问节点数的题。博主大学基础课专业知识属实不扎实，做这种题特别头疼，我用的应该属于是本方法。

首先判断这2021个叶节点应该是出现在哪一层的，第c层的节点数是 2 ^ ( c - 1 )

for c in range(1, 100):
    if pow(2, c-1) >= 2021:
        print(c, pow(2, c-1))
        break
# 输出 12 2048

输出12 和 2048，说明当该树为满二叉树时，第12层的叶子节点为2048个，超过了题目给定的2021个，因此第12层肯定是不满的。我们需要“修剪”第12层的叶子节点。

那么如何修剪呢？当我们修剪掉 1 个叶子节点，那么树的总叶子数会 -1 ，当我们再次修剪 1 个叶子节点时，树的总叶子数会不变（我们剪掉1个，但上一层会露出1个新的叶子），因此综合考虑的话，我们每剪1个叶子，可以让总叶子数-1；我们每剪2个叶子，也可以让总叶子数-1。而题目问的是至少有多少个节点，因此我们要尽可能多的修剪掉多余的叶子，所以这里我们2个2个地修剪叶子！

2048个叶子 修剪到 2021个叶子，需要修剪 （2048 - 2021）* 2 = 54个叶子，即我们在第12层修掉了54个节点。那么剩下的工作就是求出一个满二叉树前12层的总节点数，然后剪掉这54个节点，就是答案！

res = 0
for c in range(1, 13):
    res += pow(2, c-1)
res -= 54
print(res)
输出 4041

本题描述得属实拉跨了。。。

填空题4

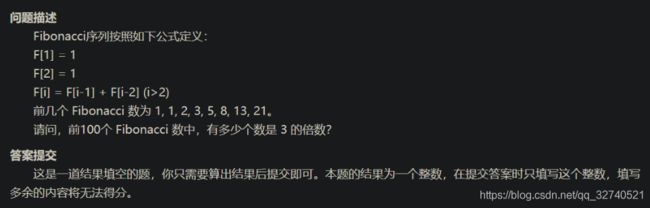
本题是斐波那契数列的题，算是对普通的斐波那契题做了一些变化，但是万变不离其宗，由于是填空题，不用关心时间复杂度（超时）问题，所以就干脆依次判断前100个斐波那契数是否满足题意即可。
斐波那契数只与前两个数有关，因此我们就用两个变量 a 和 b 保存数即可。

res = 0
a, b = 1, 1
# 遍历从第3个数开始的98个斐波那契数
for _ in range(98):
    a, b = b, a+b
    res += 1 if b % 3 == 0 else 0
print(res)
# 输出 25

这里因为要求的是前100个，然后 1（a的初值）和 1（b的初值）都不是3的倍数，因此我们直接从第3项开始，判断第3项之后的98项斐波那契数即可！

填空题5

本题截图的时候没截好，因此从别人的博客里偷的图~

题目的意思就是，每一个数所在的位置有一定的“位权”，在这个位置上的数字，要乘以该位置的“位权”，得到该位置的数值，每一个位置上的数值相加得到结果，对11取余后应该为1。

“位权”这个概念和二进制很类似，二进制数的第0位（最右位）的位权是 2 ^ 0=1，二进制数的第 i 位的位权是 2 ^ i。

本题需要注意的就是看请题设给的位权定义，稍微有点点复杂，只要求位权不写错，基本就没什么问题

s = '11010120210221999'
res = 0
for i in range(len(s)):
    res += int(s[i]) * (pow(2, (18-i-1)) % 11)
print(res % 11)
# 输出 4

我们需要添加的是最后一位数，而最后一维数的位权是1，因此前17位数的总和 + 最后一位数即为前18位数的总和，所以我们只要 + 8 即可让前18位数的总和对11取余为1
（4 + 8）% 11 = 1

故答案为 8

编程题1

第一个编程题比较简单。
考察的点应该是Python输入函数input()的细节，由于输入分4行，那么我们也要用4个input()去输入，然后还考察了input()的返回值是字符串类型，不能直接参与计算，需要先转换成int类型。

x, a, y, b = [int(input()) for _ in range(4)]
print(x * a + y * b)

也可以用比较朴素的写法：

x = int(input())
a = int(input())
y = int(input())
b = int(input())
print(x * a + y * b)

编程题2

本题考察的是Python字符串处理。
这里图没有截全，但是博主做题的时候留意过了，输入的字符串只会出现大小写字母，不会出现空格、符号之类的内容。因此可以直接使用Python字符串函数中的title()函数。

title()函数可以将字符串中的每一个单词的首字母转换成大写，同时将每一个单词的非首字母转换成小写。

print(input().title())

这里因为input()的返回值就是字符串，所以直接调用title()即可。

当然考场上万一忘记这个函数的话，可以用下标去索引去切片，然后用字符串处理函数 upper()和lower()

s = input()
print(s[0].upper() + s[1:].lower())

首先将第一个字符转换成大写，然后将第一个字母之后的所有字符转换成小写。

upper()函数可以将字符串中所有的小写字母转换成大写。
lower()函数可以将字符串中所有的大写字母转换成小写。
当加号的操作数为字符串时，作用是字符串拼接。

编程题3

本题在考场上没有想优化的解法，也不知道有没有，应该会有通过某种特殊数据结构去优化的算法吧，我猜的。

这里博主就是直接模拟栈的出入情况，然后就能得出答案

t = int(input())
for _ in range(t):
    n = int(input())
    nums = list(map(int, input().split()))
    res, stack = [], []
    for target in range(1, n+1):
        while target not in stack and nums:
            stack.append(nums.pop(0))
        if target == stack[-1]:
            res.append(stack.pop())
        elif target == stack[0]:
            res.append(stack.pop(0))
        else:
            print('NO')
            res = []
            break
    if res:
        print('YES')

我们每一次输出的目标（target）依次从1到 n，当栈中不存在target时，说明应该从输入数组nums中依次入栈。

经过一系列入栈操作后，target出现在栈中，此时如果target在栈中的位置是栈顶或栈底，那么就可以顺利出栈。我们顺势以同样方法遍历下一个target。

但是，如果target出现在栈中的位置既不是栈顶也不是栈底，那么我们就无法顺利出栈，故该输入不能依题意顺序出栈，应该输出NO。

编程题4

本题考察的是滑动窗口，但是复杂度不高，所以用本方法应该也能解出来，依次输出每一个存在变化都的位置的变化都即可（这句话好绕口）。

n = int(input())
nums = list(map(int, input().split()))
res = []

for p in range(2, n-2):
    res.append(max(nums[p-2:p+3]) - min(nums[p-2:p+3]))
print(*res, sep=' ')

这里截图没截出来，但是博主特意留意过，输入数组的长度是大于等于5的，所以我们可以放心地从下标2开始遍历到n-2。

对于每一个位置，我们找出 [p-2: p+3]之间的最大值和最小值，做差即为该位置 p 的变化度，注意Python切片遵循“左闭右开”原则。

另外提一下输出列表中所有元素，每一个元素之间用空格隔开，最后不能有多余空格的方法。通过Python的星号表达式，将列表“解压”成一个个单独的元素，然后用print()函数中的sep参数控制间隔符为空格即可。

print(*res, sep=' ')

编程题5

蓝桥杯动态规划题！本题作为压轴题，和前面的题相比，难度上还是有一些差距的。

博主备考蓝桥杯期间一直重视动态规划，刷的是力扣上的“动态规划精讲（一）”这本leetbook（不是打广告，免费的）。

按照那本leetbook上的思路，本题的输入有两个串，因此属于“双串问题”，而在双串输入的基础上，本题还带有维度k（公共子序列的长度），所以上升到“双串带维度问题”。

如果是一般的“双串问题”，那么就想到用一个二维DP解决；如果是“双串带维度问题”，那么就用一个三维DP去解决。

大致思路定了，接下来就是动态规划基本套路了：

1、状态定义：dp[i][j][p] 为 在A串前 i 个字符与B串前 j 个字符中取出长度为 p 的公共子序列的取法数量。

2、状态转移方程：本题状态转移需要关注的点比较简单，就是A串和B串的最后一个字符是否相同，相同是一个状态转移方程，不相同又是另一个状态转移方程。

当 A串的第 i 个字符 和 B串的第 j 个字符相同时，状态转移方程为：
dp[i][j][p] =
dp[i - 1][j - 1][p - 1] + dp[i - 1][j][p] + dp[i][j - 1][p] - dp[i - 1][j - 1][p]

解释：
1）dp[i - 1][j - 1][p - 1]，不看相同的两串最后一个字符，从A的 前i-1个字符和 B的 前 j-1 个字符中取长度为 p-1 的公共子序列的取法数。

2）dp[i - 1][j][p] + dp[i][j - 1][p]，不采用相同的两串最后一个字符，只看A串的 前 i-1 和 B 的 前 j，以及只看A串的 前i 和 B串的 前 j-1 中取长度为 p 公共子序列的取法数。

3）dp[i - 1][j - 1][p]，第二点中的两项存在重复部分，这里减去的是上两项的重复部分。

当 A串的第 i 个字符 和 B串的第 j 个字符不相同时，状态转移方程为：
dp[i][j][p] = dp[i - 1][j][p] + dp[i][j - 1][p] -
dp[i - 1][j - 1][p]

解释：
1）dp[i - 1][j][p] + dp[i][j - 1][p]，不采用相同的两串最后一个字符，只看A串的 前 i-1 和 B 的 前 j，以及只看A串的 前i 和 B串的 前 j-1 中取长度为 p 公共子序列的取法数。

因为我们不需要去看 A[i] 和 B[j] 了，他俩不相同，我们应该去看 A[i-1] 和 B[ j ] 以及 A[ i ] 和 B[ j - 1]。

2）dp[i - 1][j - 1][p]，第二点中的两项存在重复部分，这里减去的是上两项的重复部分。

3、边界条件
本题的边界条件有三，其实为二：

1）维度 p 为 0 时，dp的值为多少。
我们通过定义的状态来思考这个问题，dp[i][j][0] 指的是，在A串的前 i 个字符 和 B串的 前 j 个字符中取长度为 0 的公共子序列的取法数。

我们要取一个长度为0的公共子序列，那不就是取一个空字符串嘛，那就只有 1 种取法嘛！所以当 p 为 0 时，dp值为1。

2） p 大于 i 或 j 怎么办？
当 p 大于 i 或 p 大于 j 时，我们举个例子 i = 2， j = 4， p = 3，我们要做的是从长度 分别为 2 和 4 的串中取出一个长度为3的公共子序列，这显然是做不到的嘛，我A串总共才长度2，因此此时 dp 值为 0

定义完上述的三点（状态、状态转移方程、边界条件）后，就可以敲代码了：

n, m, k = list(map(int, input().split()))
A = list(map(int, input().split()))
B = list(map(int, input().split()))
mod = 1000007

dp = [[[0 for _ in range(k + 1)] for _ in range(m + 1)] for _ in range(n + 1)]

for i in range(n + 1):
    for j in range(m + 1):
        dp[i][j][0] = 1
        
for i in range(1, n + 1):
    for j in range(1, m + 1):
        for p in range(1, k + 1):
            # 边界条件
            if p == 0:
                dp[i][j][0] = 1
            if p > i or p > j:
                dp[i][j][p] = 0
            elif A[i - 1] == B[j - 1]:
                dp[i][j][p] = (dp[i - 1][j - 1][p - 1] + dp[i - 1][j][p] + dp[i][j - 1][p] - dp[i - 1][j - 1][p]) % mod
            elif A[i - 1] != B[j - 1]:
                dp[i][j][p] = (dp[i - 1][j][p] + dp[i][j - 1][p] - dp[i - 1][j - 1][p]) % mod

print(dp[-1][-1][-1])

另外稍微要注意的就是，本题的dp值是要取模的，因此状态转移时，每一次做完加减后应该取一次模，然后最后输出答案时就不用取模了。

当然也可以状态转移时不取模，最后输出答案时再取模，但是这样不太好，运算过程会很慢！